九上数学铅锤法怎么做

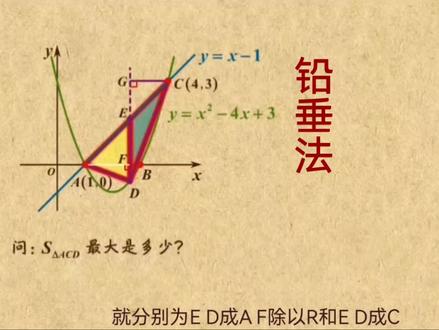
在这个视频里，咱先来看个例子，比如抛物线 y 等于 x， 方减四， x 加三与 x 轴有两交点 a 和 b 与过 a 点的直线 y 等于 x 减一，相交于点 c。 如果在抛物线上有个动点 d， 且位于直线 a c 的下方，问你三角形 acd 的面积最大是多少？这里要求的是三角形的面积， 那根据公式，三角形 acd 的面积就等于底成高除以二。如果咱就以 ac 为例的话，那相应的高就是这条。 其中 a 和 c 这俩点咱都知道，那这条线段的长度就可以求，不过这条高也就是点地到 ac 的距离，貌似不太好求，因此这条路走不通，那咱就换个方向试试看， 要求的是三角形 acd 的面积，除了直接计算之外，咱还可以把它切成多个三角形分别计算。比如从地点向上做一条数值的线段第一，那整个三角形 就被咱分成了 ab 和 cd 这俩小三角形。如果以 ed 为 d 的话，那这个三角形的高也就是 af， 而这个三角形的高就是 cg， 那这俩三角形的面积就分别为 ed 乘 af 除以二和 ed 乘 cd 除以二了。 因此三角形 acd 的面积就等于异地乘这俩高的和除以二，不难发现，这俩高的和不就恰好等于 ac， 这两点合作标的差吗？也就是四点一得三，因此三角形 acd 的面积就等于异地乘三除以二，记二分之三倍的异地了。要想让这个面积达到最大值，那就得让异地最长才行。 由于点翼和点地的横坐标相同，咱就设这两点的坐标，分别为 x y 一和 x y 二，不难看出，线段异地的长度就等于这两点的纵坐标，外一与 y 的差的绝对值。在这里，直线位于抛物线的上访，那异地也就等于 y 一减 y 二了。又由于点 在值线上，那外一就等于 x 减一，而点地在抛物线上，那外二就等于 x 方减四， x 加三。因此， e d 就等于判两个叉化解一下，也就是负 x 方加五， x 减四了，这不就是个二三数吗？要想求他的最大值，只需要配个方即可。 先给等号右边提取个负号就得。负到 x 方减五， x 加四，这里是五，那咱就得加一个二分之五的平方，再把它减掉即可。到此，这三东西就可以应时分解为 x 减二分之五的平方，而后面这俩合并下，也就是负四分之九， 再把这个符号盛进去，那结果也就是负 x 减二分之五的平方加上四分之九了。很明显，当 x 等于二分之五时，等式右边这部分就得零，此时线段异地的长度就取得了最大值记四分之九了。把它带进这个式子，那三角形 acd 的面积就等于二分之三 成四分之九算一，算得八分之二十七了，这就是最后的结果。好了，就讲这么多，总结一下，在这里要求这种三角形的面积，咱可以从这点向上做一条竖直的线段，把这个三角形分成两部分分别计算。 而这条线段异地的长度，其实就是直线与抛物线之间的垂直距离。要想把它求出来，那你就得先求出这两点的综合标，而他俩的差距绝对值就是这条线段的长度了。至于态度最直吗？只需要用配方来求即可。怎么样，听懂了吧？

每天一分钟学会压轴题，在代纪综合题中一个必会的技巧，求任意三角形面积的方法，先垂宪法， 那什么是千锤宪法呢？首先，三角形面积公式我们都知道是二分之一底乘以高，这里我们把高换成千锤高，把底换成水平宽，就是我们的千锤宪法。 那千锤高和水平宽又是什么呢？图中我们分别从三点向 x 轴做垂线，蓝色线段即是我们的千锤高，绿色线段就是我们的水平宽。 证明这个公式一点都不难。我们把这两个三角形标记为一号和二号，此时大三角形面积就等于两个小三角形面积之和。我们将蓝色线段看成底边，分别引出垂线，此时两个小三角形面积就能表示成这个样子。合并同类 向后，不难发现，我们的 h 一加 h 二不就是绿色线段的长度吗？至此，我们的公式证明完毕，我们只需求出蓝色和绿色线段长度这道题就可以解决了。 因为点 b 的横坐标是二点， c 的横坐标是八，轻松可得。水平宽 e、 f 就是两点，横坐标之差等于六，此时只需求出 ad 长度即可。这条线段又垂直于 x 轴，所以 b 点横坐标等于 a 点，横坐标也就是五， 并且他又在 bc 上，我们根据 bc 两点坐标可以求出这条线段的解析式，再将地点的横坐标带入，即可求出他的坐标。 所以千锤高 ad 不就是两点，纵坐标之差等于五吗？最后，带入我们的千锤线公式，答案不就出来了吗？同学们，你学会了吗？

哈喽，朋友们，一个视频教会大家理解依次函数中已知三角形的面积求动点坐标的问题。那么我们来看一下， p 点是直线 y 等于负三 x 下面的一个动点已知三角形 a b， p 的面积呢，是等于二零二四的，最后要求这个动点 p 的坐标。 好，那么拿到这个问题啊，最终的落脚点肯定是想办法把面积表示出来，令他等于二零二四，构建等量关系式对不对？如何去表示面积呢？哎，自然想到我们之前所讲的什么 千垂法，但是千垂法表示三角形面积，前提是不是你得先把这三个点的坐标给表示出来？在这我们已经知道 a 点和 b 点是这个三角形两个定点， p 点相当于是一个 带确定的动点，所以我们先把 p 点的坐标进行一个假设，横坐标我们设为 m 的话，因为它在这条直线外点负三 x 上中坐标，这就是负三 m。 好，那么有了 p 点坐标，接下来是不是就可以构建我们的千锤法了？呃，从理论上来说啊，从 b 点、 a 点以及我们 p 点都是可以的。但是我在这给大家说一下，我们在遇到两定移动的这种问题的时候呢，往往从这个动点去构造千锤高或者是水平线解决问题，为什么呢？因为这样的计算要简单直白一些。好，我们来操作一下。 好，那么在这的话呢，我们已经构建了我们的千锤高， pq 很明显面积就可以表示为二分之 pq 乘以另外两个点 ab 的水平宽，是这个道理吧。呃，那么我们还得先把 q 点的坐标算一下，这样才能够把 pq 的长度给表示出来， q 点的横坐标就是 m 纵坐标，是不是就得先求出 a b 的直线解析式，然后，哎，令横坐标等于 m 就可以得到对应的纵坐标啊。 那么带领系数啊， l a b 它应该是 y 等于咱们的负三分之一 x 加三分之八，这个我就不多说了。呃，横坐标为 m 乘坐标就是负三分之一 m 加上三分之八，那至此我们的 p q 是不是就可以表示 出来？拿我们纵坐标做差也就可以了，负三分之一 m 加三分之八，再减去 p 点的纵坐标，也就是加上三 m 啊，最后它是等于多少？等于我们的三分之八 m 加三分之八。好，那我想问一下， 我们的千锤高是否就是这个表达式呢？在这就要千万千万要注意了，大家一定要想清楚， p 点它其实是一个动点，它既然是个动点，它是不是就有可能在 a p 的什么 a b 这条直线的什么 下翻，也有可能在 a b 这条直线的上翻，那我们来看一下，如果他是在直线的上翻，是怎样一个情境啊？ 好，那在这的话呢，我们把 a b p 假设就是 p 一撇放到哎，我们 a b 这条直线的上方，很明显我依旧构造我们的千锤高交于我们的这个直线啊， a b 与 q 一撇，那在这儿我们 p 一撇的电影坐标，如果我依旧设为 m 负三 m 的话， q 一撇的坐标毋庸置疑还是 m 负三分之一 m 加三分之八，是不是这个道理？但是此时此刻 p 一撇， q 一撇的长度还是这个吗？ 那就不是了，为什么？因为这个时候 p 一撇点是在 q 一撇的上方，它的长度应该是拿 p 一撇的正坐标负三 m 减去 q 一撇的坐标，它， 这其实说白了，是不是就是他的什么相反数啊？所以啊，在这种问题的时候，解决的时候呢，大家一定一定要注意，加上一个什么 绝对值，是不是就能够轻松化解这个问题？那接下来我觉得就轻松了，我们最终的面积也就是二分之一乘以，哎， p q 三分之八， m 加三分之 八的绝对值，那么再乘以一个水平宽，这个水平宽我就不详细说了啊，五减去二就好了，最后是等于二零二四的，那这个的话呢，毋庸置疑是有两个结果的，对不对啊？你自己去进行 个化解，得到的应该是四 m 加四的绝对值啊，等于咱们的二零二四。那么一种情况，四 m 加四 等于二零二四，那么 m 就等于多少？呃， m 就等于我们的五百零五，那么对应 p 点的坐标横坐标就是五百零五，纵坐标就是负的，呃，乘以负三吗？对不对？负一五一五。好。那另一种情况是不是就是，哎，四 m 加四等于负的二零二四，那么此时 m 他应该是等于负的 五百零七的，那么自然 p 点此时对应的坐标就是负五百零七，纵坐标乘以一个负三，也就是一五二一。 所以最终这个题目应该是有两种情况，通过这个题目，我希望大家能够深刻的理解千乘法求面积啊，他是非常的好用的，一方面，我们在遇到两定移动的这类问题的时候，我们往往从这个动 重点出发，构造一个什么啊？千锤高或者是水平的线去解决问题，那么在这呢就一定要注意这个千锤高啊，你要判断一下需不需要套绝对值符号，那么通过一个绝对值符号呢？我们就不会出现移动情况的问题，那么你学会了吗？

妈妈们，让老师讲一下二字函数动点类的问题，那么这一类型问题呢，经常考在中考亚洲题部分，今天老师给出两种方法，一种是千锤法，一种是平移法， 总有一法是你喜欢的。咱们看题目给了一个二次函数和一次函数，让你去求三角形 bcp 面积的最大值。点 p 呢，是 bc 这条直线上的抛物线上的一个动点。 那么想要去求 p c b 面积的最大值呢？先来跟老师了解一下千锤法的基本原理。 假设呢，老师把这个三角形给你画出来，这里是点 p、 点 c 和点 b 千锤。千锤，咱们知道他是竖直往下的，所以呢，老师过点屁 做一条线段，让它和 b c 交于点 q， 那这个时候三角形 p b c 就分成了左右两个三角形啦，它的面积呢，就等于三角形 p c q 加上三角形 p b q 啦。那假设呢，这里是它的高，叫做 h e， 那这个高呢，咱们叫做一个 h 二，咱们都是以 p q 为底的。那好，整个 p c q 的面积呢，就等于二分之一的 p q 乘以 h 一， 再加上 p b q 的面积呢，就等于二分之一的 p q 乘以 h 二。发现什么啦，二分之一 的 p q 可以给它提出来，那就是二分之一 p q 乘以括号里边是 h 一加 h 二啦。 那这一部分呢，我们叫做千锤高，而这一部分呢，叫做水平宽。水平宽呢，其实就是 b c 两点间的一个水平的距离。那么对于这道题来说呢， b c 两点间的水平距离是不是就是三呀？ 对吧？也就是他是确定的一个三，你想让整个三角形的面积最大，那咱们只要求出 p q 的最大值就可以啦，那跟老师呢，来看具体的题目， 咱们过点 p 向下做一条线段，和 b c 呢，交于点 q， 那这个时候咱们看一下 p q 这条线段该如何去表示 p 点呢？是在抛物线上的一个动点，咱们可以设它的点的坐标是 m， 然后带入到抛物线解析式当中去，负的 m 的平方加上两倍的 m， 再给他加上一个三， 而点 q 和点 p 的横坐标是相同的，那就是 m 纵坐标呢，因为它在 b c 这条直线上， a 带进来，那就是一个负 m 加上三捺 p q 线段的长度呢，就是大的点减小的点，动作标做一个叉啊，高的点减低的点，所以这条线段的解析式呢，我们表示成负的 m 的平方加上 二， m 加上三，再减去一个 q 点的纵坐标负 m 加上三。注意啊，咱们来整理一下负的 m 的平方加上二， m 加三，然后呢，负负得正， 加上一个二 m， 然后再减去一个三，正负三呢，抵消掉了，这里是正的 m 啊，那就是负的 m 的平方加上一个三倍的 m。 想要去求 p q 的一个最大值， 咱们有一种方法呢，可以通过配方来做，还有一种方法呢，你可以通过套公式来做，那老师呢，把它配方一下，哎，先把负一提出去，那里边就是 m 的平方减去一个三倍的 m， 你要配什么呢？ 你要配的是一次相记数一半的平方，那就是加上二分之三括号的平方，这里变成中括号，那这里呢，加了一个四分之九，但是 前面有个括号，那就相当于减一个四分之九呢，咱们需要再给它加上一个四分之九啦。那整个括号里边就是 m 减去二分之三括号的平方再加上四分之九。 也就是说，当 m 等于二分之三的时候，发现什么啦？二分之三是一点五对吧？和老师画的位置呢比较接近哎，当 m 等于二分之三的时候，你的 p q 它是有最大值的。最大值等于多少呢？就是 四分之九啦啊， p q 的最大值有啦，给它带进来一乘就可以啦。那么这个方法呢？妈妈们赶快截屏保存起来，给孩子们看下个视频呢，老师来讲平移法。好啦，下课！

hello， 一个视频教会大家理解平面直角坐标系中三角形面积求解的非常重要方法，千锤法。我们来看一下这个问题呢，是非常直观的，就是求这样一个三角形 a b、 c 的面积。 那么我们其实都知道啊，在一个平面直角坐标系中的三角形，如果他存在一条边是什么水平的线或者是竖直的线，那这个面积就比较好操作，为什么呢？ 往往就可以直接以这个水平线或者是竖直线为底，那么另一个点到他的距离作为我们的高，而这个底和高是不是肯定都是好球的呀，自然面积也就呼之欲出，但是你会发现，对于这个三角形 abc 来说，这个方法好像并不那么适用，因为他没有一条边是水平或竖直的，那该怎么办呢？ 没有条件，自然我们要创造条件，所以我们想着利用割补的思想去进行一个哎构造。在这的话呢，我们先尝试一下从 a 点啊 可以做一条竖直的线，那么这个时候呢，与直线 b c 啊交于点 p， 其实这个 a p 呢，就是我们的千锤糕。 那么在这呢，我们通过这样一个 ap 啊，就把三角形 abc 的面积分成了左右两部分，而且他们都是以 ap 可以理解为矮为底，那么对应的一个高是不是也都可以呈现出来，所以在这我们可以把它的面积啊进行一个表达 好。那么在这的话呢，我们通过割补法得到左右两边的面积分别是什么？二分之一 a p 乘以 h e 以及二分之一 a p 乘以我们的 h 二，对不对？那在这的话呢，依旧可以继续进行合并同类项，也就是二分之一， a p 乘以 h 一加 h 二，接下来就是我们的重点了，这个 h 一加 h 二该怎么理解呢？我们从 b 点啊往下引一条竖直的线，那这个时候接下来我怎么做呢？我把 h 一啊进行一个延 长，他与我们的这个竖直线会产生一个交点，那么这一段其实很明显，是不是也是我们的 h 二呀？其实你会发现，那 h 一加 h 二也就是这个的长度，这个长度其实本质就相当于什么， 是不是就是我们 c 点和 b 点他们两个点的什么水平距离啊？所以这个长度其实就是我们所称之的水平宽。 好，那么自然我们这个面积啊，水平宽已经知道了，其实说白了，也就是我们 b 点和 c 点横坐标差值的绝对值，那也就是 x b 减 x c 的绝对值，再说 x b 和 x c 的绝对值，我觉得，哎，差值绝对值很好想吧，这是三减去负五等于八，所以也就是二分之一乘，八乘它也就是四乘以我们的 a p， 那接下来我们只需要把 a p 算出来是不是就可以了？怎么算 a p 呢？因为 a 点和 p 点是不是数值的两个点啊？那么自然我只要知道 p 点的纵坐标，拿三减去它的纵坐标就可以了，如何得到它的一个纵坐标呢？因为我知道它的横坐标又在直线 哎， b c 上，所以把 b c 的直线解释式先搞定就好了。 l b c， 那这个的话呢，你自己带定系数啊，其实不用解，也就是 y 等于八分之三， x 减去八分之一。 呃，当我们的 x 等于一的时候啊，很容易求出来对应的 y 是等于我们的什么呢？四分之一的，那也就意味着 p 点的坐标就是多少一四分之一， 所以我是不是就可以求出我们 a p 的一个长度啊？ a p 的长度呢？三减去四分之，也就是四分之十一，至此我们这个面积是不是也就哎，非常轻松了？四乘以四分之十一，最后答案是十一。当然啊，如果你觉得做到这，你已经非常理解我们的千锤法，那就大错特错。我们能 来看一下另一种情况，我们刚刚是不是过点 a 做了一条竖直线啊？那么问题就是我可不可以过 b 点或 c 点做竖直线呢？我们来模拟一下，假设我现在过的是 b 点做竖直线，那自然他和 ac 就应该交于他们的什么延长线来，我们来看一下。 好，这个时候呢，得到了这样一个三角形，我们的 c p b。 哎，那你说这个怎么去求我们的 a b c 面积啊？ 所以在这你要想的足够通透。其实说白了，我们这有两个以数值边 p b 为哎，底边的三角形，我们的 p b c 以及 p a b， 而我们的 a b c 是不是就可以理解为是大三角形 p b c 减去这个小三角形 p b a 的面积啊？那接下来我只需要把 这个的高以及这边上的高都给他表达出来，是不是依旧可以沿用之前的思路，我们来写一下。好，那么在这的话呢，我们把这两个三角形 的呃 p b 边的高都呈现出来了，假设这个 h 一，这个 h 二，所以最后得到的是什么呢？面积 a b c 啊，也就是二分之一 p b 乘以 h 一减去 h 二。好，那么同 干干的一个思路，我们来看一下 h 一减 h 二到底代表着什么？我们同样从 a 点啊往下引一条竖直的线，那这个时候呢？假设这个点啊是在这，很明显这个长度是不是也就是 h 二啊？所以你会发现， h 一减去 h 二，其实说白了是不就是这一段的一个长度啊？ 那么这段长度其实说白了就是什么？是不就是 c 点和 a 点的水平宽呀？ 同样是水平宽，哎，那么这个时候我觉得就很好理解了吧，可以改写成二分之一乘以 p b 乘以我们的 x a 减去 x c 的一个绝对值。呃，那么最后的一个 算呢？我觉得就和之前是不是如出一辙了？我们来对比一下这两种做法他们的共同点，其实你会发现我们都是先找到任意一个点做什么？做竖直线，哎，做的这个竖直线与另外两个点所在的直线交点，其实就是我们的什么 千锤高，也就是我们的面积二分之一乘以千锤高，然后再乘以什么呢？你会发现，如果是过点 a 做的这个竖直线，那么最后这个水平宽，其实恰好就是 b 点和 c 点也是另外两个点的水平宽，对不对？ 如果我这个点是过我们的什么点 b 做的千锤高，那接下来自然最后的水平宽，你会发现就是另外两个点 a 和 c 点的水平宽，是这个道理吧？所以我们的面积也就是二分之一千锤高乘以水平宽。那至此，我觉得你是不是就可以统一起来了， 我们过任意一个点其实都可以这么去构造，当然啊，最后我希望大家可以再去思考一个问题，但是除了我们过这些点，三个顶点做竖直线可以构造，能否做水平线构造呢？好，那么今天的一个分享就到这，你学会了吗？