四年级上册数学滑梯模型怎么做
粉丝6867获赞2.5万
相关视频
 04:18查看AI文稿AI文稿
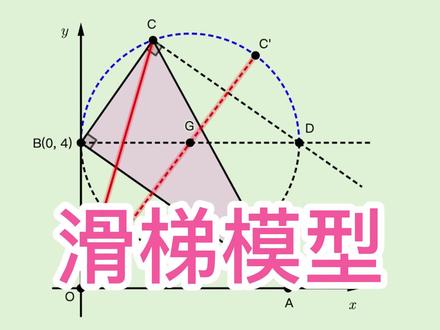
04:18查看AI文稿AI文稿中考压轴题来看一个滑梯模型的题目,说 b 点坐标为零。四、三角形 abc 是直角,三角形 a 点在 x 轴正慢走上滑动,并且在滑动过程中保持三角形 abc 的面积为定值十二。 让我们求现代 oc 长度的最大值。好,这道题如果不掌握技巧的去死算,多半会凉凉。 题目要求 oc 的最大值, o 点是定点, c 点是动点,我们只需要找出 c 点的运动轨迹即可。这道题的关键在于利用和转化三角形 abc 的面积。转化三角形面积 的惯用剂量是做平行线,由于是要找十一点的运动轨迹,我们过十一点做一条直线与 ab 平行, 那么对于直线上的任意一点 p 都有 s, 三角形 abp 等于 s, 三角形 abc 等于十二。至于 p 点要取到哪一个位置,我们接着往下分析。 我们还有必点坐标,您是这个条件没有使用。显然欧币的长度为四。前面告诉了我们三角形的面积,我们能不能以欧币为高构造三角形来计算面积呢? 过闭点做一条直线平行于 x 轴,那么对于这条直线上的任意点 q 都有三、 三角形 abq 的高为 ob, 我们不妨设这两条平行线交于地点 来考察三角形 abd 的面积。由于地点在直线 cd 上,那么 s 三角形 abd 等于 s, 三角形 abc 等于十二, 同时地点也在 bd 这条直线上,那么三角形 abd 的高为 ob, 而三角形 abd 的面积为十二,那么底边 bd 的长度为六, 也就是 b d 的长度为定值。注意到 b 点是定点,那么 d 点也是定点。注意到 cd 平行于 ab, 而角 abc 等于九十度, 那么角 bcd 也等于九十度。我们来考察三角形 bcd, 角 bcd 等于九十度,是定值角 bcd 所对应的边 bd 是固定的,这是典型的定边定角问题。 c 点的运动轨迹是一个圆,更确切的说, c 点的运动轨迹是蓝色的。这一段壶 不熟悉定边定角模型的小伙伴可以参考这个视频。 好,我们回到题目,不妨设这个圆的圆心为基点。由于角 bcd 等于九十度,那么 bd 是这个圆的直径,基点是线段 bd 的终点, 这个圆的半径 gd 等于直径 bd 的一半,等于三。弄清楚 c 点的运动轨迹后,我们再来看看线段 oc 的最大值。注意到 o 点是定点, 原机为定原, c 点在原机上运动,那么 oc 什么时候能取到最大值呢?显然,这是传说中的一箭穿心 连接。 og 胶原基于 cp, 当且仅当 c 点与 cp 重合时, oc 能取到最大值 ocp。 来算一算 ocp 的长度, gcp 是原 g 的半径,长度为三。 og 的长度根据高谷定理,它等于根号下四的平方,加三的平方等于五,因此 oc 的最大值为 ocp 等于八。
2091rosan 01:40
01:40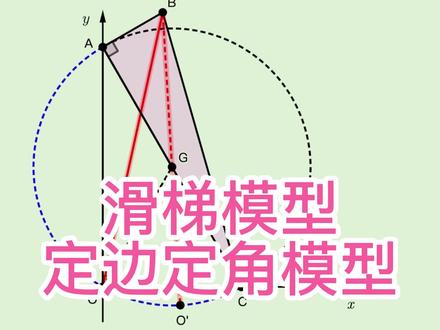 02:59查看AI文稿AI文稿
02:59查看AI文稿AI文稿数学基本功来看一个滑梯模型的题目,说三角形 abc 是直角三角形,一个直角边的长度为一,另外一个直角边的长度为四。 a 点在外轴正半途上滑动, c 点在 x 轴正半途上滑动。 让我们求线段 ob 长度的最大值。好,显然, o 点是定点, b 点是动点。如果能找出 b 点的运动轨迹,那么问题就能很快解决。事实上, b 点的运动轨迹是一个椭圆,我们很难处理,所以这里需要换一种思路。 前面我们说 o 点是定点, b 点是动点,这种运动规律是以直角坐标系为参考系的。学过物理的小 小伙伴应该都知道,运动是相对的,如果我们换一种坐标系,运动规律又该如何呢?比如我们以三角形 abc 为参考系,那么 b 点就是定点, o 点是动点。题目要求 ob 的最大值,我们只需要找出 o 点的运动轨迹即可。 我们来考察直角三角形 aoc, 角 aoc 等于九十度,是定值,角 aoc 对应的边 ac 长度为四,也是定值,这是典型的定边定角问题。 欧典的运动轨迹是一个圆,更确切的说,欧典的运动轨迹是蓝色的。这一段壶 不熟悉定边定角模型的小伙伴可以参考这个视频。 好,我们回到题目,不妨射这个圆的圆心为积点,由于角 aoc 等于九十度,那么 ac 是圆肌的直径,积点是 ac 的终点。我们再来看看线段 ob 的最大值, b 点是定点, 圆肌是定圆, o 点在圆肌上运动,那么 ob 什么时候能取到最大值呢?显然,这是传说中的一箭穿心 连接 b g 将圆基于 o 一撇,当接紧到 o 点与 o 一撇重合时, o b 能取到最大值 o 一撇 b。 当然,我们也可以通过连接 og, 通过三角形 ogb 两边之和大于第三边来论证这一点, 来算算 o 撇 b 的长度。 o 撇积是原机的半径,长度是直径 a c 的一半等于二 g b 的长度根据高谷定理,等于根号下一的平方,加二的平方等于根号五。 因此,现在 o b 的最大值等于 o e 撇 b 等于二,加根号五。
1329rosan 02:12
02:12














