求值域的方法分离常数法
粉丝6.1万获赞81.0万
相关视频
 15:00查看AI文稿AI文稿
15:00查看AI文稿AI文稿首先这东西哈,我们叫分离常数,就形如什么类型?形如这个分子,这里,这里是干嘛?一个 a c 函数,这里是什么?一个 e c 函数,是不是?嗯,但是我不希望看到分子有 我的目标是什么?我的目标是什么?目标是是分子无 x 好不好?那么分离它?分离这个常数的方法是这样子的,注意听哈,分母是谁? 分母是谁?就是这个 x 加一,那么请把分母抄一遍,然后把分母再抄一遍。 抄两遍可不可以为了横等变换,你看原本这个分子的 x 的系数是谁?是不是二?嗯,那这里会保, 保证去括号之后是二,前面要乘个谁哦,二是不是跟得上吗?那么这里去括号,这里是不是多了一个二?多一个二就要干嘛?是不是减一个二,然后这个三是不是原本就有的?嗯,跟不跟上,然后化减下这个四就变成了什么了? 这里就变成了这个二 x 加一,然后你干嘛?是不是加一,除以 x 加一?好,把分子拆开, 就变成了二 x 加一,除以谁 x 加一,加上谁 x 加一,分是谁除一,这里有多少?这是二加上谁? 你看分子,我们达到我们目标,没有分子,没有谁,是不是做到了?这个过程叫什么?分离常数?各位家长,谢谢。好,这边按个暂停,然后 做个笔记,然后重重做一遍,从这边等下我们举一反三。怎么回事哈,我们来看画完重新自己画一遍之后那个词语怎么求的。首先因为这个式子 这个地方一加这个一,除以 x 加一是不是不等于零的?是不是?所以呢,这个加满二呢,就会不等于谁? 是不等于二,所以就是说这个值域是干嘛?是 y 不等于二。各位各位小学生好,画图,然后再交往。我们 其实刚刚总结下那个方法哈,就是分母抄一遍,分母再抄一遍,再把分子凑出来就可以了,是不是?好,我们看到一道例子看,看到一道例子啊,请大家把这个给我求个值,欲 把分母敲一遍,把分母再敲一遍试试。看 来时间到了哈,我们来看看。首先是分母超了个三 x 加一,这就是超了个三 x 加一,为了使得分子的这个系数为谁是不二,括号前面要乘以谁, 是不是三分之二?嗯,好,三分之二一乘进去,这里是不是多了个三分之二?嗯,多一个数在干嘛?减一个数,哦,这个减一原本是不是就有了那一化减数变成了这样子, 这里负三分之二跟减一是变成负三分之五,然后分子拆开就是变成了这样的,然后这里就变成了三分之二。个码减去三, x 加一分之谁三分之五,因为他不等于谁, 不等于零,对不对?所以这个不等于谁,是不是三分之二,理解了吗?嗯,好。然后星系的同学会发现,三分之二正好是 x 的系数跟 x 的系数,是不是?嗯,好,上一道题,这里他不等于谁,所以不等于二。最后答案是 y 不等于二,对不对?这里 x 是不是?是谁是不是一?这里谁是不是?谁 是不是啊?所以当我们用公式去推导的时候,就可以推出一个结论来,这个地方假如我把它改成 ax 加 bcx 加 d, 按照公式去推导之后呢,就会发现他就不直接不等于谁,是不是七分之 a? 是不是?是分子跟分母?这个 x 的什么是不是系数,明白了吗?但是,呃,偷懒的情况下,你可以把这个结论记下来,以后做选择题,很快,但是我关键是要教会你这个分拆的技巧,因为等一下要画图,你不会分拆,你就不会画图,明白了吗? 可以把这个结论记一记,以后做选择填空题的时候可以快很多。这个推导过程有兴趣可以记,没兴趣可以不记,直接记第一行跟最后一行就可以了,是不是?但是刚刚那个例子那些你一定要会分开, 那么接下来求职就已经解决了,是不是?尤其是有这个简便公式,是可以特别快,那接下来怎么样去画图呢?那我们回到前面来总结一下哈,分子分母都是依次函数的方法,叫分离系数法啊,分离长数法,说错了,打错 长数好,然后令分子 vx。 那么关键是这个图该怎么画出来呢?好,其实这个图呢,我们在初中就学过一个一个函数叫什么反比例函数,我们先做个回顾,好不好看,怎么画?比如说大家看到这个图没有? 看到这个图了吗?这个是一个反比例函数 k 什么数?是不是正的过什么上限?是不是一三?是不是靠近 x 轴永不, x 轴跟 y 轴永不相交,是不是?是不是?好,那如果分母加个一呢? 左加右减,是不是形成一个什么什么什么关系,是不是左右平移?所以怎么样平移呢?我们是不是在这里画条什么线,是不是虚线?相当于把这个歪轴是不是平移过来? 是永远靠近永不,干嘛就香蕉。那么如果在这里 x 减二呢?是往右平两格,永远靠近,永不相加。如果在外面再加一个数呢?如果再加多一个数呢? 是不是上下平移?是不是?所以分拆成这种目的的话,其实是为了方便 画图,然后刚刚这个地方我分拆成了什么?是不二加谁? x 加一分之一,是不是?那我画图的时候呢?大家养成一个习惯,先分拆。如果我要画出这个图, 我该怎么办?我们首先是先画哪一个图片?画最基础的,谁就二十分之一,二十分之一过什么上限呢? 是一三象限可以吗?好,永远靠近,永不相交。好,那么现在他加一呢?往左边平一格,加二呢?往上往上平两格。所以我们看怎么样去画这个虚线啊?我们尽量用尺子铅笔画好一点 啊,我们重新划走一次,用尺子跟铅笔尽量画工整一点。刚才说往左边拼多少格? 这个是画条虚线。这是谁?是负一好往上两格呢?就这样子 可以吗?这里是不二跟不跟上?嗯,然后永远靠近,永不相交,是相相当于还是一相上线?这样子是不是类似于这样?可以理解吗?永远靠近,永不相交,可不可以理解?我现在这里看着有点相交哈,不要介意。 可以可以理解吗?明不明白?所以如果你不会分拆的话,你是画不出这个图来的。 听没听懂?那么画图是为了什么呢?等下会告诉你,大家先尝试着自己把这个图自己再画一遍,动手。你们为什么是往左哈左加右减? 左边的左左加右减,左加右减的意思是指原本这个 x 发生了什么变化? x 是不是换成了 x 加一 啊?上下下剪是指什么?是外面,在在外面的的上下下剪,下剪可以吗?上下下剪,哎呀,错失了可以吗?有问题。那画这图什么用呢?很快就知道了。 呃,我们学函数有个特点,就是这个计算很严谨,画图要非常好,那么很多题目都可以很轻松的做出来。呃,比方来说,我们来看这道题,一个一个同学的一个考试题目来的。 y 等于 x 加二分之三在零到五上的最大值跟什么最大值?就 x 属于零到五了 是不是?好,只要你把这个草图画出来就很直观的。这个图该怎么设计?其实其实就是哪哪个图 y 等于谁?是 x 分之三,这个是不是反比例函数?嗯,如果一三上线的把它变成谁,就变成了 y 等于谁。 x 加二分之谁是三,往往哪边平移,左加 右键往左边多个单位,两个单位把图画出来,然后去找那两个点,一秒试一下,把你们动作试下,造题。 好的差不多了哈,我们一起来。画完了,我们一起来,其实就是把左边这个虚线还是要画的哈,记得拼多少格是不两格,这里是负二对吧?啊,那个图像画出来的是不是这样子?可不可以? 那他问什么是不是零到五的?什么 x 在哪里?是不是零到五的最大?这个最好是,这是零,这是干嘛?五可不可以零?所以这一段是不是单调地什么的是不是递减?那么也就是说当 x 为多少 为零的时候, y 是取的最大值, y 有多少,再进去是二分之三,明白吗?当 x 有多少为五的时候, y 是取的最小值多少 啊?我带进去多少就是七分之谁是不是三就两个结果自己加就可以了,明白了吗?记住,有图会让我们学数学的时候特别的安心,会特别的安心,所以你平,你平常学任何函数,第一件事情很关键的就是要学会干嘛? 画图,画图可以让题目变得简单、直观,简单而且很直观,而且非常重要,明白吗?好,那我们逐渐把题目再变得再复杂一点,好不好?再复杂一点,呃,同学们来看这道题, 再告诉你, y 等于二, x 加二分之二, x 减一对不对?一算数,一算数,然后告诉你,这里有两问哈。第一问是告诉你 x 属于五到十,好,在这里都是求值欲的。 好,然后现在这里告诉你 x。 第二个问题,告诉你什么负三到负二并上,负二到哪里?到一,是不是也是求什么值欲,明白吗?那我们关键是要把它图画出来,要画了图,我们首先要把它进行一个分离,长竖能不理解? 好,请完整的做一遍呢?给我检查一下,把图画好看点,尺子,铅笔,橡皮擦。嗯,这个分离常数应该很熟练呢, 就是分子跟分母干嘛就抄一遍,分母干嘛再抄一遍。加个括号好不好?前面要乘以多少就乘个二,就是,那么去括号是不是多了个四?是不是要减四?减四,再减,再减个谁? 整个一可不可以?可不可以唱?就这里一变,变成什么了?就这里,这里会变,这里一拆开变成什么了?说,是不是二,干嘛?我写快点加上谁 x 加二分之谁是负,嗯?对不对?好,那么这个该怎么样去分拆它呢?我可不可以现在 先画了一个谁 f x 分是谁是负,然后再画了一个谁 x 加二分之谁,是不是往往往哪边平移?是往左边平移,然后呢?再往干嘛? 再往上干嘛?两格,可不可以理解啊?这意思好,所以最终画出来的图是什么样子的? k 次复数过什么象限,什么象限?是不是一二次象限,明白吗?来画曲线的时候到了, 这是负二好,往上平移两格,这里就是二好,已经分拆出来是二,加上 x 加二分之负五,是不是拿出 x 分之负五,然后往左平两格,再往上平移两格?我们是先画好了虚线,他们这里是负五和, 是过什么?是不二次降线,所以画出来的草图是不是应该是这样子的?可以吧?好,然后他要求第一问,是要求这个 x 属于哪个地方,是不是五到哪里十?这五到十,从这个图来看的话,他是 d 什么的, 是不是递增呢?可不可以递增的话,那么只要带这个 x 的两个端点去算 y 就可以了嘛?是不是?明白吧?当 x 为为五的时候,这个 y 是不是取得最小值?是不是?当这个 y 等于谁 是十的时候,他是不是取了这个?呃,这个,这个 x 等于十的时候, y 是不是取了什么值?就这样子告诉我,这个刚刚最小值是谁?谁? 这个最小值是七分之九是吧?好,然后最大值呢?十二分之十九,十二分之十九。所以呢,第一问的结果, y 属于哪个范围? 就是七分之九到哪里?十二分之十九,明不明白?可以理解吗?好,那我们看第二问,第二问的话他说 x 属于哪个地方? 就是这个负三到哪里是负二,那负三大概是在这个位置, 可以吗?然后负二是不是这里?那么图像的话是不是往上走的?这一,这一小段是不是这一段?嗯,对不对?他是,他是一直靠近负二,是不是一直往上走?嗯嗯。有没有最大值?没有,没有,是不是有个最小值?嗯,最小值,谁是不是负三? x 为这个负三的时候带进去歪了多少? 是不是七?七跟不上?嗯,所以第一段是不 y 干嘛?是不是大于谁?是不是七?嗯,那还有一段负二在哪里?一,一大概在这个位置,然后是一,好不好?是不是?图像?是不是 这一段?是不是?他是不是一直往下走?是不是没有最小值?但这里是不是有个小小的一个大值?是不是?好,我们算一下当 x 为一的时候, y 有多少 站进去动作快点,三分之一,三分之一,三分之一。哈,那看这个图,他这里是不是一直往下走? 是不是?所以歪干嘛?是不是小于谁?是不是三分之一?明白,没有。所以就合在一起是什么?就第二问,合在一起什么意思?父,无穷。
263数学樱木 00:38查看AI文稿AI文稿
00:38查看AI文稿AI文稿分离常数法秒分数之域,第一个一次项系数比三比一,所以 y 不等于三。第二个一次性系数比一比一,所以 y 不等于一。第三个一次项系数比负,一比二,所以 y 不等于负的二分之一。 那二次型的二次项系数比负,一比正一,那是负一,这是开区间长数项之比一比一,这是 b 区间。第二个二次项系数比一比一,是一个开区间 那么长竖向支笔三比一,是一个 b 区间。最后一个二次向细数笔一比一,这是一个开区间那么长竖向支笔负一比二,这是一个 b 区间。秒掉孩子们,分离长竖法怎么证明?评论区留给你!
2496王垚博士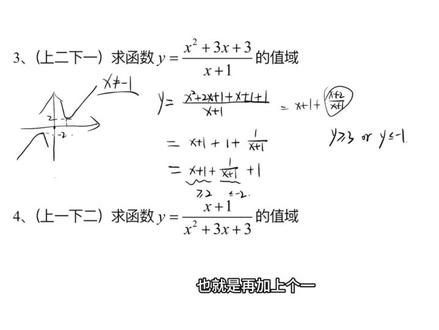 06:55查看AI文稿AI文稿
06:55查看AI文稿AI文稿分式函数求值域是其中期末的一个必考知识,也是其他模块的一个重要考察步骤。那么今天呢,这个视频就给大家讲一下分式函数如何求值域。好,我们上来看第一个题, 上边是二, s 加三,下边是 s 加一,中间是分式分数线,然后求外的取值范围。这题我们可以怎么去做呢?可以把上边去凑底下的倍数写成二, x 加二,然后再加一,把这个三拆开,那这样就可以写成 x 加一分之一,加上一个二, 这个我们可以认为是由 x 分之一向左平移一个单位,变成 x 加一分之一,再向上平移两个单位啊,变成这个东西。所以我们知道第一步来说的话,因为图像的左右平移并不会影响它最大值最小值变化,所以到这为止还是外部等于零 啊,然后它再向上平移两个单位,就会变成外部等于二。给大家画一下图像来说的话,你看 x 分之一是这个样子的,然后 x 加一分之一啊,是这个样子的 啊,然后向左拼一,我画的不太标准啊,但是再向上拼一两个单位,那就是这个样子,你会发现只有这条线,也就是二,这条线是取不到的,所以说它就是整体来说,它的答案是 white 等于二。 当然如果说你想更简单的做道题,比如说一秒就做出来,那你也可以记一个结论,就是当你遇到的式子是 y 等于 a, x 加 b, 比上 c, x 加 d 的时候,那它的值域就是 y 不等于 c 分之 a 啊,就是这个。所以第二个你看二, x 减一, x 加一, 这是二,这是一,所以说他的值于什么?外部等于二,当然得是符合这个形式,上下其次都是依次才可以这么去做, 大家明白吧?然后如果说上边比底下次数高了,我们该怎么去办?比如说我们来看这个题,上边是二次,底下是一次,那这个时候呢?如果上边比底下次数高了,我们就不要去凑底下的倍数了, 先去凑底的平方,比如先去凑 x 加一的平方,这就是 x 方加上二, x 加一,但是后边是三, x 加三,对不对?所以还差一个 x, 还差一个二,但这个二呢?可以换成加一。加一。为什么要这么做? 就是我们要去凑底下的平方,底下的倍数啊,直到最后上边没有变量。比如说这可以写成 x 加一,加上一,再加上一个 x 加一分 之一,也就是你的这个位置,你的这个位置,他不要有变量,最后只剩长数,你就可以停止了啊。 比如说有的同学在这写到了什么呢? x 加一,加上 x 加一分之, x 加二,他就不会做了,他觉得,哎,这没办法去求了呀,你要做的事,最后上面只剩下长数,那这样子的话,加上一个 x, 加一分之一,再加一。 如果,哎,看过前面视频的同学应该知道,这就可以用基本不等式了,因为他是大于等于二的。但是我们要注意一个点,基本不等式的使用条件是全正,但是这个时候他很显然他是可以取到负的, 对不对?它是可以取到负的,虽然,哎,它的定义是 x 不等于负一,我们可以不考虑为零的这个事,但是它是可以取到负值的,所以,哎,这是一个非常明显的对勾函数,对勾函数是涨 这个样子,因为形状像对勾,所以我们这么称呼他,他是关于圆点是对称的,那比如说这是二,这就是负二,所以说如果你是大于等于二的,那你就是小于等于负二的,两边各有一个范围。那最后外的答案就是什么呢?外大于等于三或外小于等于负一, 大家明白吧?也就是再加上个一,给他加一,给他加一就可以了,那最后答案就是这个东西啊,大家会做这个了吧? 在这需要注意的点就是什么呢?一定要考虑两种情况,那如果说是上一下二的,如果说上边是一次,下边是二次,比如我把这个东西颠倒过来,那你不就没有办法去像这么去做的吗? ok, 虽然他没有办法向上面这个题去做了,但是我们上面这个题都会做了,底下和上面互为倒数,我们把四变成三去做不就 ok 了吗? 也就是把它变成外分之一去做,那你的外分之一的答案是不是有的呀?对不对?所以那你看。但是变成外分之一的时候,我们先考虑一个事情,就是外是否能为零,因为如果他变成分母的话,他是不能为零的,所以你看另, s 等于负一是, y 是等于零的,所以可以取到,可以取到这个,哎,那么,哎, x 不等于负一是, 那你是不是就是 y 分之一等于 x 加一分之 x 方加三, x 加三,那你是不是就相当于 y 分之一大于等于三,或 y 分之一小于等于负一。那你这个时候再去求 y 的范围是不就可以了? y 的范围怎么求啊?你看取中间,这时候假设横着,这是 y, 这是 y 分之 一, ok, 他的作,他的图像就是这个样子的。那你看这是三,三对应的是多少?对应的外置,当外等于三分之一的时候,外分之一等于三,当外等于 负一的时候,对不对?然后,哎, y 分之一等于负一,所以说,那你看他取的是什么?哎,比三分之一,嗯,你看 y 分之一,比三还要大,然后比负一还要小, 也就是这个外分之一的范围。你看外,这个是外分之一的值,他是往上走的和这往下走的,那你对应的外值是不是取的是中间这一部分?中间这一部分啊?所以说,那我们就可以得到一个事,就是外是什么呢?小于等于 三分之一,对不对?大于零或者是 y 小于零,大 等于负一,对不对?所以说得到这个答案,最后两种情况是要干什么?是要取并级的,所以综上所述,综上 从上的话,那你就是 y 的范围就是什么 y 小于等于三分之一,大于等于负一 啊,我这还写错了,要注意主源啊,这别写成 x, 这是 y, 嗯, 就这么回事,大家明白了吧。所以说最后答案就是你也可以写成这样,负一到三分之一啊,区间的形式,集合或区间都 ok。 那么这个题如果说你感觉哎万分之一,那我能不能不变成万分之一呢?他其实原理不变的情况下,我们还可以换一种写法,就是他可以写成什么呢?上下同除以 x 加一,上面是一, 下边就是 x, 方加三, x 加三,比上 x 加一啊,你会发现原理是相同的,依然是通过求出它的取值范围,再求出一个整体的取值范围,大家明白了吧?
521冯老师聊数学(高中版) 04:58查看AI文稿AI文稿
04:58查看AI文稿AI文稿下面呢,我们来看一种求函数指域的方法,叫做分离长数法, 那么我们在高一函数的学习当中呢?呃,经常会遇到求函数值域的问题,那么其中有一类方法叫做分离长数法,这种方法主要适用于分式结构的函数, 那么下面呢,我们就具体的举两个例子来看一下如何使用这种方法。首先我们来看第一个, 第一个函数是 y 等于二, x 加三,比是 x 加一,其中 x 是有范围的, x 是大于等于一的,那么像这种分子分母都是一次函数的,我们可以使用 分离常数法,那什么叫做分离常数法?那就是我们把这个表达式当中分子当中的这个 x, 把它分离出来,把这个长数分出来,分离之后让分子不含有变量。 好,我们具体看一下怎么去操作。二, x 加三,比上 x 加一,那么怎么把这个分子当中的 x 给它分离出来,我们可以把分子凑成和分母一样的结构, 那下面是 x 加一,那上面呢,我把它,我们把它凑成跟 s 加一的倍数相关的,那就是二, x 应该是加二再加一。 好,那么我们把它拆开,拆开来写就二, s 加二,比上 s 加一就等于二,再加上一,比上 x 加一, 这样我们就把这个长数分离出来,分离之后分子就不含有变量 x, 然后我们再结合现在的这个函数的单调性来求对应函数的值域, 那么后面显然是一个反比例型的函数,那这里边我们要注意注意什么呢? x 有范,这个 x 是大于等于一的, 那我们这里边可以根据 x 二点一,我们整体求出 x 加一的范围是大于等于二, s 加一大一点二,这个整体大一点二,那么再取倒数,他的范围应该是什么? 我们把 s 加一看成整体,他是一个反比例型的函数,我们结合反比的函数图像看反比例函数,呃,我们假设 s 加一等于 t 的话,那就是梯分之一,这个梯是大于等于二的,我们看 二,在这那等于二的时候,对应的函数值是二分之一,那么大于等于二,他这函数值应该是二分之一,到哪呢?越来越小,接近于零,因此这个是 x 加一分之一, 他应该是在什么范围里呢?应该是在零到二分之一这个范围。然后我们再加一个二,前面就是二,加上一比 s 加一,这个范围就应该是 是二到二分之五,因此我们第一个题他的直域就是二到二分之五。 好,我们接着再来看一个题。第二题,第二题, y 等于三减 x, b 上二, x 减一,求他的指欲,呃,求他的指欲呢?我们仍然可以使用分离长竖法, 那么把分子凑成和分母一样的结构,分母是二, x 减一, 那么分子我们看把 x 拿前面来,负, x 跟下边乘倍数,那么这个应该是加一个多少呢?是不是应该加一个二分之一?由于原来 三,那后边再应该加一个二分之五。好,那么把前面这个整体和下边相除,我们得出来一个,有一个长数是负的二分之一,再加上后边是二分之五,比上二, x 减一。 好,那么求这个函数值域,这个函数前面是个长数,后边这个表达是不等于零,所以整个这个函数就是 y 不等于负二分之一,所以就是 y 不等于负二分之一,他的值欲 好,这就是利用分离常数法求函数之一。
918延龙高中数学 00:45查看AI文稿AI文稿
00:45查看AI文稿AI文稿话说求函数指月的方法中用的最多的是哪一个呢?哎,没错,分离常数法。什么分离常数法你都不会,赶紧把视频看完。所谓的分离常数就是通过拼凑变形,将分式函数写成只有分布有位置数,分子没有位置数,然后加上一个常数的形式。那具体怎么操作呢?比如这道题, fx 我们可以去进行拼凑,下边 x 加二,上边凑一个 x 加二。那当然我们加了一个是叫减四, 后面还有减一等于二,减去 x 加二分之五,就将 fx 分离,长了分子没有位置数,分母有位置数,然后加上一个长数的形式。接下来要求直率,就是砍瓜切菜,所以直率一到七分之九,你学会了没有?明天我们开始上难度。
1451DZT老谢高中数学
猜你喜欢
- 1566杜 老师
最新视频
- 4752李老师在上海














