夹逼定理和泰勒公式
粉丝8462获赞5.1万
相关视频
![夹逼定理,如此简单![高等数学5] #高等数学 #夹逼定理#数列极限](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/2d78fcac7f26edbcce228acd415833ca~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079104400&x-signature=VmHkkTNyTNfcjOO83zCY1eLPxKw%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=202511220142433EB98922BF180B091E0A) 12:03查看AI文稿AI文稿
12:03查看AI文稿AI文稿大家好,今天我们来讲高等数学的夹币定理,这个名字啊,起的非常合适,中间夹着无限必进,就叫夹币定理了。其实这个夹币定理的话,分成两类,一类是数列的夹币定理,另一类是函数的夹币定理。今天我们讲第一类数列的加币定理,来看吧,定义是什么呢?人家是这么说的啊,定理当然之后学完就可以直接用了。 电梯本身是这么说的,假设有三个数列,对吧?三个数列中间因为夹着,所以至少得有三个啊,然后一个是 xy z 码三个数列, 然后如果存在正整数恩零,当这个下标恩大于这个规定的这个正整数恩零的时候呢? 你注意啊,一定得保证什么?一定得保证这个 xnx 是在谁中间夹着的?是在 y 和 z 这两个数列之间夹着的。那如果说你左边和右边这两个 数列的极限都是,当 n 趋近于什么,取景于无穷的时候,左边这个极限呢?取景为确定的数字 a, 右边这个呢,也取景于确定的数字 a, 那么中间夹着的这个 x 肯定也取景于数列 a 了,那具体表示的话,人家就这么表示。你看, 当 n 区均无穷的时候, y 和 z 这两个数列都是确定的,这样一个极限都是收敛于 a 的,那么我们就可以说中间夹着的 x 也肯定收敛于 a, 这个是直观上很容易理解的,你夹着他们,因为这个 y 和 z 是夹着中间这个数列的, 那你上线和下线都趋近于确定的谁啊?我们可以画一个,你看这个呢,我们可以理解为 z, 这个没问题啊,他逐渐接近于那个确定的数字 a, 然后一直可以接近下去,那下边的话是谁呢?下边的话是这个 y 吧,那我呢, 再用这个蓝线来表示一下这个 x, 无论说当,只要当 n, 当这个下标 n 足够大的时候,中间这个 x, n 都是在中间,都是在中间夹着,他肯定更加取景 a 了,就这样一个意思, 那直观理解很好理解。那证明的话怎么去证呢?数学系的同学一定得掌握证明的方法,其他同学的话,你看懂了就行了,会用就可以啊。 来看这证明方法是这样说的啊,首先啊,你极限去进行 a, 我们之前是讲过数列极限的定义的,对不对?用的是什么?用 exclond 定义,或者说 epcolond 定义是函数极限啊, exclonn 定义呢?这个指的是数列极限, 那么既然这个 y 和 z 极限是 a 的话,那其实就是说,无论说,对于所有的正数 excel 来说啊,无论这个正数多么小,那肯定存在正 整数恩,当然这个恩的话,我们让他大于等于这个定义里头这个恩零,记住,一定得大于,等于不能小于啊。当 这个下标 n 足够大的时候,肯定是啊,这个竖着上外恩和谁的距离和确定的这个小 a 的距离肯定是小 exlon 的,包括这个 zn 也是这个呢,其实就是数列的定义,数列极限的定义之前我们讲过,你一定得看一下,如果不懂的话,去掉绝对好。里头啊, 就这个 y n 呢,他必须在 a 减 epcolon 和 a 加 epcolon 之间,然后这个 zn 也必须是啊, a 减 epcolon 和 a 加 epcon 之间,你外和 z 什么关系啊?外和 z 中间是夹着谁的? 中间是加着这个 x 的,所以说,既然这个 y 和 z 都在这个 a 减 ex 融合 a 加 ex 之间的话,那我们这个 x 肯定也是在什么之间的,在这个 a 减 e 和 a 加 excel 之间的。现在你看我画横线的这一部分,对于所有的你看好了,同学们啊,对于所有的大于零的 excel, 无论这个 excel 多么小, 总存在这样的正正说恩,使得当这个下标小恩大于这个正正说恩的时候呢,总有,你看,总有他跟 a 的距离在书桌上是小于一不松的,这个不就是书列极限的定义吗?所以就正出来了, 这个呢,数学系的同学一定得掌握。那好,讲完了,证明以后我们练一道题啊,练的话主要是讲这个定理怎么去用。看好了, 这个定理怎么去用呢?看例题,让你求证的是这样一个数列啊,他的极限啊,求,极限是等于多少?这个极限等于多少?怎么求呢?第一步,先大胆猜想呗,猜的话我肯定就猜二分之一了。有人来说,老师你是知道答案,所以你猜 二分之一,呵呵,我不知道答案,我也知道是他是才二分之一,知道为什么吗?原因很简单,大家看。 哎,每一个分母他都是几次的呀?每一个分母都是关于恩的二次的,其实就主要是这个恩二次在起作用,然后每一个分子的话,分子你不要管他,分子相比于什么,相比于这个二次来说是忽略不计的。但是 有多少个呀,有多少项啊,有 n 项,这个就不能忽略不计了啊。所以呢,从一一直加到 n, 他的话其实很好挣,他的话求出来应该是 恩方,然后二分之一恩方加恩吗?等差数点求和这个很容易,这样最后一笔的话求极限就是二分之一了。当恩确定于正无穷的时候。那既然是这样,我猜出来是二分之一,那怎么去正呢?哎,关键在于放松吗? 怎么放缩?我们先记啊。让我们求的这样一个数列呢,是 xn 先放还是先缩呀。先缩小一点点吧,就是先写这个外按,外按好说, 你说同学们看好了啊,每一个他相当于几个分式加起来啊?这个 x 相当于 n 个分式加起来,对吧? n 个分式加起来的话,你说你是改变这个分母好呢还是这个题处理这个分子好呢?我认为 处理什么好处理分母好。为什么你改变分母好呢?因为如果你把分都改成一样的形式,同分就直接就可以同分了,对不对?就很简单了。那所以说你看,我要把它缩小, 你看我所有的,哎,我第一个分母变大,哎,第二个分母再变大,所有的分母都变成恩方加恩。所有的分母除了最后一项开外啊,所有的分母是不是变大?分母变大是不是整体就要缩小了?哎呦,原来是 这个意思,所有的分母都放大了那么一丢丢都变成了恩方加恩。所以说分母放大整体就要缩小了啊。写了个小于号没问题。那缩完了还要怎么还要放大吧。好,这一步呢,是缩 是不是还得放大呀?那怎么样放大呢?哎,一样的。还是对分母进行处理吗?这个 x 针怎么放大?所有的分母都变小,第一个分母不变, 所有的分母都变成恩方加一,恩方加一,所有的分母都变成恩方加一。那既然所有的分母啊,除了第一项开外,所有的分母都变小,分母变小不就是整体变大的意思吗?你看,所有的分母,我们都变成了恩方加一了, 那继续处理呗。实际上我写到这很多同学就知道了,老师,我只需要求一下这个 y n, 他的极限是二分之一,再求一下这个 z n, 他的极限也是 二分之一。所以说根据假币定理,假币准则,中间 xn 的极限也是二分之一。那接下来你就求呗,剩下就很简单了啊, 先求谁?先求万恩呗,万恩好说,你分我都一样,我就直接通分吗?分子为什么改成这个形式?哎呀,分子就是一加二加三加四,一直加到 n 等差数列,求和二分之一,首相加尾相乘像数吗?这样的话,你看画圈这个部分就直接消掉,他其实就是二分之一啊,这么简单, 那这个 z n 呢? z n 其实也一样, z n 的话,分母啊,分母,分母是恩方加一了,这个分子的话,处理以后不能直接削,但是 我们上节课讲过,这个二恩方加上二恩,恩方加上恩,当恩趋近于无穷的时候,主要是谁在起作用啊?主要是最高次项的系数在起作用,我们直接 直接写这个二分之一就行了,对不对?那好,所以现在我们就确定了呀,不仅说无论对于任何一项啊,这个恩对于这个小恩来说,都是外恩小于 x, 恩小于 z, 恩。那既然 做左边,就是说这个 y n 的极限是二分之一, y n 的极限也是二分之一,那中间我们就直接下结论嘛,中间根据假币定理,假币准则就直接说出来 xn, 他的极限就是二分之一。 原来呀,他这个家的定力这么好用,那既然这么好用,你总得自己练一道题吧。我们再讲一道例题啊,关键在于怎么去放松 好这个极限。这个极限怎么求呢?同学们,你要让我猜的话,我直接就猜出来他肯定是五。为什么是五呢?其实一样的,跟那个多项式比,多项式最高子弹组啊, 作用一样,他这个里头也是植物的 n 次方赞助作用的。他如果让你求的是你看 根号下啊, n 次根号下五的 n 次方,那不就相当于五的 n 次方,这其实就是个常数吗?最后结果就是五,你直接写五就行了, 但是你标准过程总不能这样写,你得体现这样价位定理的过程吧。那就写呗,老老实实写,第一步怎么样?先猜,我们已经猜出来是五了,那接下来就要写这个过程了吧。过程是好的,写了啊,我们这样来写。 首先我们不妨啊,记什么记我们球的这个数列呢?就是 n 次根号下一加二 n, 再加上五 n, 我一会为了方便写,我改一下形式啊,你 n 次根号下不相当于一加二 n 加五 n 次方,分分之一次方吗?对吧? n 次 好下,相当于 n n g 次方。那关键是放缩,先放还是先缩呢?那就先缩呗,就是说先把它缩小啊,你缩小的话不是说随便缩小的,还得跟他有关系。缩小的话,这个外恩怎么缩小呢? 好说,同学们,我们每一项都把它改成什么样子?你想啊,既然我的 n 次方起主要作用,我,我前两天我就把它省略掉了,那不就小了吗? 所以说他就变成了什么?就变成了 n 次。跟号下前头不写了,零加零我就不写了啊,直接来个五的 n 次方,等于五的 n 次方,怎么样?再来个 n 分之,那其实不就是五吗? 所以说我们明显感觉到这个外恩是小于啊 xn 的,其实这个外恩就是一个常数,就是五。这个我就不多说了啊,继续看下一个放大,缩 了以后得放大。怎么样去放大啊?五的 n 次方在起作用吧。那我首先把前两项一和二的 n 次方都写上五的 n 次方,也就是说我这个字眼我要放大了。放大的话怎么放大?五的 n 次方,再加五的 n 次方,再加前两项我都写成五的 n 次方,注意是 n 次方向下。 那整理之后的话,里头不就变成了三倍的五的 n 次方吗?对吧? n 分之一次方,但是要处理, 处理成什么形式?我展开写了啊,三的 n 减一次方,再乘五的 n 次方,然后 n 减一次方,这个处理之后,实际上相当于他直接乘五了,这个没问题, 我们显然可以得到什么?显然可以得到 y n 小于 x, 这个数列小于 z n。 哎呦,中间夹准则夹臂定理不就出来了吗?看了啊,因为什么呀?因为你这个 y 的极限, 我们先求这个 y 的极限。 y 的极限他其实就是五,他就是一个长数嘛,他当然永远是五了。不管了啊,我们求哪个呢?继续来求一下这个 z 啊。继续来求一下这个 z, 当 n 区进行无穷的时候,这个 z、 n、 c、 n 相当于多少?我们仔细观察一下这个形式嘛。当 n 区进行无穷的时候,我们看这一部分啊, 三又 n 分之一次方 n 去年无穷的时候,画圈这一部分是不是就是零次方?三的零次方其实相当于是一的,对不对?就是说这一部分是一,然后再乘长数,像五一乘五,最后不还是五。哎呦,我知道了, 你看同学们,我们求回正了,被他缩小以后,他的极限是五,比他放大以后的数列呢?极限也是五。然后接下来根据甲笔定理不就求出来了吗?所以说中间这样一个数列,就是我们求的这样一个数列,他的极限是多少?他的极限直接写五就行了。 那现在你应该懂夹币定理,夹币准则了吧。那所以说留一道作业题,你自己来做这道作业题 怎么办?就是呢,是变分母还是变分子?你自己来了啊。然后最后这个极限等于几呢?过程我不说了,极限我一看我就曾能猜出来他是一的。你自己去放松吧,分享课堂知识,感受数学之美。我是张帆老师,下节课再见。
1.2万会放羊的教书匠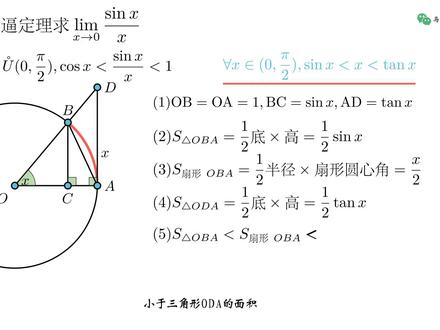 21:42查看AI文稿AI文稿
21:42查看AI文稿AI文稿关于求极限,前面我们只学习了一种方法,那就是用定义来求,运用这种方法推出了一般函数的极限、极限的运算法则等等。 而今天我们要学习的是另一种方法,用加 b 定理求极限,掌握了它,我们才能计算更复杂的极限。 加 b 定理有着非常明确的几何意义,假如这里有上下两条曲线, h x 和 g x, 它们在 x 零点处的极限均为 l, 那么夹在它们中间的这条红色曲线 f x, 它在 x 零处的极限也为 l, 其完整定义如下,它的证明也比较简单,下面以 x 区域 x 零为例进行证明。直接使用极限的定义就可以完成了。 首先根据条件一,我们可以知道,在以 x 零为中心的某个区心灵域内,有 g x 小于等于 f x 小于等于 h x。 然后根据 g x、 h x 极限均为 l, 可以得到在以 x 零为中心的某个区心灵域内, g x 减 l 的绝对值小于 excellent, h x 减 l 的绝对值也小于 excellent。 此时在半径最小的这个区西林域内,有 g x 减 l 的绝对值小于 excellent, h x 减 l 的绝对值也小于 excellent。 把绝对值打开,就可以得到这两个式子。 再根据 f x 是在 g x 和 h x 之间这个条件,就可以得到下面这个不等式, 这样就得到了函数 f x 在 x 零处的极 线也为 l, 这样就完成了证明。这里由于求的是函数极限,因此也被称为嘉宾定理的函数版。 而用于求数列极限的版本称为加 b 定理的数列版,可以看到它和函数版的内容几乎没有区别,后面我们就把它们统称为加 b 定理。 搞清楚了什么是加 b 定理,下面我们就来看几道关于它的立体。 用加 b 定理求 c x 在零处的极限分析一下。题目要用加 b 定理来计算, 那么按照定义就是要找到两个函数, f x 和 g x, 满足以下两点,一、在极限位置附近,这里就是在零点附近, sci x 的函数值要在二者之间。 第二点是 f x 和 g x 在零点处的极限均相等。怎么找这两个函数呢?可以在图像上找灵感。首先做出 c x 在零点附近的图像, 从图像上可以猜测, six 在原点的极限可能为零,那它大概就应该小于一个正数,比如 x 大于 一个负数,比如负 x, 那是不是 f x, g x 就是负 x 和 x 呢?还是做出图像来验证一下。这里看起来 c x 在零点处的极限好像确实是可以靠它们加出来, 不过很快就发现这个想法是不对的。不对的地方就在于, 这两个函数在 x 等于零点处附近都是一会小于 six, 一会又大于 six。 另外一个也是一样的, 不满足上面的条件一,因此左边写的这个不等式在 x 等于零点附近是不成。 但如果我们将上面红色部分的曲线用 g x 表示, 下面这部分用 f x 来表示, 那他们就符合条件了。 也就是说要用加必定理求 c i x 在零点处的极限,其实就是要证明,在 x 等于零的某个区心灵域内, c i x 大于等于负的 x 的绝对值,小于等于正的 x 的绝对值。 而我们从图上可以看出,不论淋浴半径取多大, six 都是落在二者之间的。不仅如此, 我们还知道 cyx 在负二分之派时取得最小值,在正二分之派时取得最大值。因此我们可以选取二分之派为去心淋浴的半径。 这样只要完成了这个证明,就可以利用加 b 定理完成计算。 好的分析完了,下面开始证明。我们把证明分为两部分, 第一部分就是要证明在零到二分之 pi 这个区间上, six 大于等于负的 x 的绝对值,小于等于正的 x 的绝对值。 而第二部分就是要证明负二分之拍到零这个区间上, si x 也是大于等于负的 x 的绝对值,小于等于正的 x 的绝对值。 首先证明第一部分 做出一个半径唯一的单位源, 并在上面做出一段弧 a b, 令这段弧长为 x。 注意,这里 x 是大于零小于二分之派的。 根据弧长的定义,它所对应的圆心角 a o b, 其弧度值也就为 x。 然后过闭点做 o a 的垂线, b c 连接 a b。 由于这里是单位圆,因此 o b 等于一, b, c 等于 c x, 那么三角形 o, b, c 的面积就等于二分之 c x, 而扇形 o、 b, a, 它的面积等于二分之 x。 并且从左图我们可以看出,三角形 o、 b, a 的面积小于扇形 o b, a 的面积。 这样就可以得到在零到二分之派这段区间上, sine x 是大于零小于 x 的。 根据它,我们就很容易就能得出结论一,正确 结论一,证明完后,结论二就很好证明了。 由于 side x 是奇函数,那么就有负的 side x 等于 side 负 x。 然后结合结论一,就能推出负的 side x 大于负 x 的绝对值,小于 x 的绝对值 也就得到 sign 负 x 大于负 x 的绝对值小于 x 的绝对值, 这就是结论二。这样根据结论一结论二, 我们就证明出了。三 x 在以零为中心,半径为二分之派的去心淋浴内,其值大于负 x 的绝对值小于 x 的绝对值。 除此以外,负 x 的绝对值和 x 的绝对值在零点处的极限为零,那么根据加 b 定理,就能计算出 c x 在零点处的极限为零, 至此就完成了这道题。 用家必定理求 cosin x 在零处的极限。和前面求 six 的时候一样, 还是先来分析一下。求 sine x 的时候我们说过,就是要找到两个函数, f x 和 g x, 满足以下两点, 一,在极限位置附近,这里就是在零点附近, cosi x 的函数值要在二者之间。 第二点是 f x 和 g x 在零点处的极限均相等。前面我们是靠图像来求解的 six, 这次我们尝试用代数的方法来求解这道题。 首先看第一步,我们可以先找出 x 的一个合适的去心淋浴,和求 cy x 是一样,这里可以取半径为二分 分之 pad 取心领域,在这个取值范围内,我们知道余弦函数 cosi x, 它的取值范围是在零到一之间的。而根据背角公式,我们又知道 cosi x 由等于一减去两倍 sign 平方二分之 x。 根据前面求 si x 得出的这个结论,化减后可以得到 cosi x 最终大于。这个式子 整理后就是 cosi x 大于一减去二分之 x 平方,根据这两个不等式, 最终得到 cosin x, 再一减去二分之 x 平方于一之间。这样我们就找到了合适的 f x 与 g x。 接下来我们来看第二步两侧极限是否相等。这两个极限都很简单, 因为一减去二分之 x 平方的极限为一,且长数一的极限也为一,因此两侧极限相等条件成立,最终得出 cosin x 在零处的极限为一。 最后我们可以画出图像观察一下,可以看到 cosi x 的图像确实在一与一减二分之 x 平方之间, 且他们在原点处的极限均为零。 用加 b 定理,求 sine x 除以 x 在零处的极限。这道题的做法和前面的例题一样,第一步,找出一个范围,这一题 sine x 除以 x 的范围在 cosine x 于一之间。 这个式子是解题的关键,关于他是如何得出的,后面我们会详细讲,然后对不等式两边分别求极限,得到两端极限都为一, 这样就解出了。三 x 除以 x 在零处的极限为一。这就是这道题的完整过程。 其他的步骤都比较简单,关键就是要列出这个不等式, 要对这个式子进行证明。要用到我们高中时学习的一个结论,在零到二分之派这段区间上, si x 小于 x, 小于 tangent x。 下面我们先来证明这个结论。 做出一个半径唯一的单位源, 并在上面做出一段弧 a b, 令这段弧长为 x。 注意这里 x 是大于零小于二分之派的。 根据弧长的定义,它所对应的圆心角 a o b, 其弧度值也就为 x, 然后过 b 点做 o a 的垂线 b c, 然后过 a 点做 o a 的垂线, o b 的延长线与垂线交于点地连接 a, b。 由于这里是单位圆,因此 o, b 等于 o, a 等于一, b, c 等于 c, i, x, a, d 等于 tangent x。 那么三角形 o, b, c 的面积就等于二分之 c, i, x, 而扇形 o, b, a, 它的面积等于二分之 x, 三角形 o, d, a 的面积就等于二分之 tangent x。 并且从左图我们可以看出,三角形 o, b, a 的面积小于扇形 o, b, a 的面积小于三角形 o, d, a 的面积。 这样就可以得到在零到二分之派这段区间上, sine x 小于 x 小于 tangent x 的这样就推出了这个结论。 这个结论证明完后,我们要证明的这个条件就很简单了, 在零到二分之派这段区间上, si x 小于 x 小于 tangent x 的不等式,每一项同时除以 si x, 得到这个新的不等式, 新的不等式每一项取导数最终得到 cosine x 小于 sine x 除以 x 小于一,也就是在零到二分之派满足 cosine x 小于 sine x 除以 x 小于一。 我们可以画出图像观察一下,可以看到三个函数确实满足不等式关系,并且三个函数都是偶函数, 因此有在负二分之拍到零满足 cosi x 小于 si, x 除以 x 小于一, 这样我们就得出了这个范围。回到前面写出的解题过程,值得注意的是 这道题的答案三, x 除以 x 在零处的极限为一,它是一个很重要的极限,在后面解题中我们经常会用到它。下节课我们就来看几道例题,学习一下加 b 定理和这个重要极限的运用。 运用加 b 定理与重要的极限计算这几个式子的极限,下面一道一道的开始看。先来看第一题,这是一道很基础的练习题, 以前我们用无穷小的乘法计算过这道题,这次我们用加 b 定理来进行计算。由于负一小于等于三, x 小于等于一, 我们可以将不等式每一项除以 x。 根据 x 大于零和小于零可以得到两个不等式。写出来是这样的, 对于不等式,两端分别求极限,可以得到左右两边的极限都等于零, 因此所求极限的结果为零,这样我们就解除了这道题。下面我们来看第二题。第二题要计算的这个极限, 可以用重要的极限三, x 除以 x 在零点极限为一来进行计算。先将式子进行以下变形, tangent, x 除以 x 可以写成两个分, 可以对这两个分式分别求极限。分式求极限,可以对分子分母分别求极限。观察这个式子,可以看到 左边这是重要的极限等于一,右边这个极限也等于一, 因此最终结果等于一乘上一,也就是一。这样就解出了第二题的答案。下面我们来看第三题。 第三题要计算的这个极限,也可以用重要的极限三, x 除以 x 在零点极限为一来进行计算。先将式子进行以下变形,分子分母 同时呈上一家 cosine, x 得到这个式子,分子可以写成 same 平方, x 同样可以将这个式子写成两个分式的乘积, 然后对每个成绩分别求极限。对于这两个极限,左边是重要的极限的平方等于一,右边这个极限等于二分之一, 因此最终结果等于二分之一。这样就解出了第三题的答案。下面我们来看最后一题。 第四题的这个极限,我们用加必定理来解决它。 这道题题目里有不太常见的符号,在求解这道题之前,我们先来了解一下这个符号是什么意思。这是向上驱正符号, 它的意思很简单,我们来看两个例子就知道了。先来看第一个,一点一向上取整, 我们就将小数部分省去,整数部分加一,最终结果为二。同样的一点九,向上取整也等于二, 而整数向上取整等于自己。例如二向上取整等于二,这就是这个符号的意义了。了解了这个 个,我们可以开始来解这道例题了。由于 x 分之一小于等于 x 分之一,向上取整小于一,加上 x 分之一, 我们可以将不等式每一项乘上 x, 由于这里的 x 都大于零,因此可以得到这个式子。 对于不等式两端分别求极限,可以得到左右两边的极限都等于一, 因此所求极限的结果为一。这样我们就解除了这道题。这节课我们学习了加 b 定理和重要的极限。 下节课开始,我们来学习复合函数的极限。以上是本期视频的全部内容,欢迎一键三连。
105马同学图解数学![泰勒公式及麦克劳林公式[高等数学18] #高等数学 #大学数学 #泰勒公式 #麦克劳林公式 #考研](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/57521bcec3873972387aeb313690041b~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079104400&x-signature=obAolq0g%2BBNklN2cT4es5sA7Eg0%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=202511220142433EB98922BF180B091E0A) 15:24查看AI文稿AI文稿
15:24查看AI文稿AI文稿大家好,今天我们就来讲一下泰勒公式和麦克劳令公式,那什么叫泰勒公式呢?你来看啊,这讲内容分两部分,第一部分的话就是简单介绍一下这个泰勒公式和麦克劳令公式。第二部分的话,还得讲一下这个泰勒中式定理,还有拉格朗有一项究竟是什么东西。咱们先来看这个第一部分吧。 第一部分的话说这个态度定理啊,那什么叫态度定理呢?来看了,如果说函数 fx 再点 x 零处,由 n 阶倒数,你有 n 阶的话呢? n 减一减二减二减零就都有了,对吧?然后那么就会有怎样的一个结论呢? 那么就会有这样一个结论,这个结论指的是 fx 等于 fx 零,这个 fx 零指的是某一个点处 x 零,这个点处的函数值啊,这个带 x 的部分才是这个变量的啊, x 零是一个确定的值啊,然后这个 x 是一个变量,一定注意这一点, 然后就等于。哎呦,后边还是挺有意思的。二,那如他中间如果再继续往后写第一项,第二项,第三项,那接下来要写的话,那就是三的阶层分支 f 三街道的书,我就写成片片片 x 零。好,那后边是不是还得依据这样一个规律,还得写成 x 减 x 零或者三次方,懂了吧?那继续往后他有 n 接的话,但是究竟有没有 n 加一接,人家没说,所以后边的话,如果有 n 加一接,你可以一直往下洗啊。 嗯,但是如果再往下没有 n 加一阶倒数的话,那就只能写成这样一个鱼像的形式了。那究竟这个 rnx 究竟是什么东西呢?咱现在就告诉你啊, 这个后边啊, x 这个知道叫什么符号吧?这不就是一个无穷小量的意思吗?我写一下,其实这个就叫 fx 无穷小亮,他要这么写的话,那就指的是 x 减 x 零这样一个 n 次方 这样一个函数的无穷小量。好了,这是一个无穷小。那继续来说,那公式一的话就称为什么?实际上我想说的这个 r n x, 他指的他的名字叫做佩亚诺鱼像,知道这个佩亚诺是一个名字就行了啊, 然后称为带佩亚诺鱼像的泰勒公式。原来这个公式就叫泰勒公式啊,然后具体来说的话,就要带佩亚诺鱼像的泰勒公式,那有些时候用的还是挺多的,如果说哈,如果说我只保留这个前两项的话,咱们你喝一下啊, fx 等于 fx 零,加上 f 片 x 零,然后 x 减去 x 零,因为你后边很可能还有这个鱼像,对吧?所以我们暂时先写上这个约,等于你和了一下,就接近了一下。那我要再写的话,很多同学就知道了,你这个 fx 就是 y, 嗯,我这个 y 零,这个 x 零, fx 零的话,我不妨就写成这个约等于什么?约等于外零,给我移过来呗。外减外零等于,这个不就是某一店主的什么切线的意义,不就是斜率吗? k x 减 x 零,我的天呐,所以呢,他经常利用这样一个 精确到哪,精确到一些导数的部分,经常来这样一个线性的礼盒,这个用的是非常多的,在数学分析里头,经过这样的线性礼盒之后呢,可以大大降低数学分析的难度,你到之后学数学分析自然而然就明白了。 那好,继续往后,接下我们就要证明一下这个态度定理了,那怎么去证明这样一个态度定理呢?告诉大家,实际上呢,并不难证明,我们需要这么来写,主要是想证明啊,这个 rnx 他是一个无穷小量,是关于什么呢?是关于这样一个 x 减 x 零 n 次方的无穷小量。嗯, 怎么去写?咱们一步一步来啊,那我就写这样画横线的部分啊,前头就写成什么,写成这样一个耒合的符号啊,这样一个求和,求和的话,这个求和下标是多少?那我就写成 i 等于零啊,因为是从这个零接到数,从原原函数开始写的, 然后 i 的切成分支 f 哦 i 街道数所对应的 x 零处的 ij 导数,然后再写 x 减 x 零 i 次方。好,这么来写, 那这么来写的话,那所以说呀,我这个 rnx 不就相当于 fx 减去红色的部分,红色部分我们就写成这样一个求和的部分啊,我指的是红色的部分,所以说这个 rnx 是不是变成这个样子了呀?当然需要注意的是一点什么呢? 我们其实在中间是规定了,规定这个零阶岛数十项就是圆函数本身这个是已经规定好了,并且规定什么呢?规定这 零的接成,它本身就是等于一的,这样的话就符合要求了。那么我们再继续往下写啊,当你写出这个样子来以后,接下来我们是不是只需要证明什么? 我们接下来只用证明,因为你是想证明后边他是谁的,是这样一个 x 键 x 零 n 次方的无情小量。无情小量的定义不就是写我们上边是不是可以一直去求到的呀?然后下边也可以一直去求到的呀?而且上边和下边都是当 x 去运用 x 零时候,都什么 啊?无穷小亮,所以说无穷小亮比上无穷小亮。零比零的性质,你看左边是不是零比零啊?他是一个零,既然符合零比零的不定时的话,那接下来是不是要利用诺贝达法则?诺贝达法则我们一直求道嘛,对不对? 左边我就直接写了画圈部分呢,整体我就写成左边这个狮子了,左边这个狮子一接倒数,二接倒数,一只写到多少?一只写到 n 接导书我就一直写下去了,我省略了很多东西的啊。下边你经过 n 次求逃,第一次求导的话是 n 乘 x 减 x, 零的 n 减一次方,那第二次求的话就变成了 n 成什么? n 乘 n 减一,再乘 x 减 x, 零的 n 减二次方,就一直求导下去,最终的话就求逃成为什么了?经过 n 次求导 就变成了 n 乘 n 减一,乘 n 减二,一直乘到一,那其实最终结果它不就是 n 的阶层?原来分母是 n 的阶层啊,那这个分子的话也不麻烦,因为分子的话,我们看 分子就是这个 r x 吧。 r x 分成两部分,左边这一部分的话,你经过 n 次求导,那不就是 f n x n 接倒数吗?对吧?那后边求和部分的话,大家一定要注意,求和部分的话,我们展开时间就是红线部分,大家能看出来这样一个红色的部分吧,这就是 r x 后边这样一个部分。你经过 n 次求导, 同学们告诉我经过一次修道画圈部分得几?因为他是一个常数,经过一次修道得零吧。但是我们要经过 n 次修道啊,经过第二修道时候他也变成零了, 第三个球岛时候他也变成零,所以经过第 n 字球岛以后只剩下最后一部分了。那既然只剩下最后一部分,最后一部分怎么写?我就直接写出来吧。我就直接写了最后一部分。经过 n 字球岛以后,这个 r x, 他就是 fn 接导数。谁呀? x 零所对应的 n 接导数。 那最终结果,因为 x 需选 x 零,你把 x 零带入这个位置,最终结果不就是零吗?所以说这个 r n x 这样一个培养的鱼像,他是不是一个无穷小量啊?他当然是一个无穷小量,谁都无穷小量, x 键 x 零 n 次放的五成小料。是不是证明完了?证明完泰勒定律了呀?那继续往后说,接下来就是这个泰勒公式和买卡罗定公式啊。现在我们来说一下这个 泰勒展开的唯一性。刚才说过了啊,说过你展开以后呢?一次方,二次方这样一个规律,最后太带这样一个培养的鱼像, 那么他是不是唯一的呢?就是说展开成这样一个规律之后,这个 a 零是否一定对应的是这个 f x 零?那这个 a 二的话,是否就一定对应的是二的阶层分支? f p r x 零是不是一定这样?我告诉大家,肯定是唯一的,一会我会帮助你证明一下的啊, 肯定是唯一的。后边告诉你了,这个鱼像也满足他就是 x 加 x 变蓝字方这样一个函数的无穷小, 那么一定有这样一个规律,发现了,发现了,没有,他就是告诉你,泰勒展开肯定是唯一的 a, 零是一个确定的数字,然后 a 一呢,也是一个确定的数字, a 二, a 三一直到 a 都是一个确定的数字。那具体来说怎么证明?我跟大家说一下。证明的话,因为需要用到红色部分这样一个公式, 我们先看题,接下来他让你证明什么?证明泰勒展开唯一性定理。怎样证明这个唯一性定理呢?我只能说是类似于数学归纳法,但是不能叫数学归纳法。那好了,我们证明了啊,证明的话,我们让 k 等于几啊? k 最小,他是自然,那肯定是 k 等于零的时候啊, 可以等于零,可以等于零的话,那左边的话,我们就将 x 零带入第一个这样一个式子中, 那待会以后左边就变成了 fx 零了,右边就变成了 a 零了,后边你看这是多少啊?零啊, a 二乘零啊, a 三,后边都是零,我们就不写了。所以说你看第一部分球队老爸,第二部分我们看对不对啊? 当这个 k 等于一的时候呢?他这个规律是告诉我们什么?告诉我们 a 一等于一的结成分值,实际上也就是 f px, 怎么证呢?这个呢,也要说我们先求到一次啊, f 片 x 对谁啊?对,这样一个式子求导一次,以后常数求导零,我们就不写了啊。好,第二部分求导以后就是 a 一, 然后第三部分呢,就是二倍的 a 二,再乘 x 加 x 零,然后后边的话就是一次方啊,然后继续往后斜那双写的就一样了,我们还是另外 x 等于 x 零,但是呢,带入上边这个式子里头,一带就带出来了 f 片 x 零,右边是 a 一,后边是什么呀?后边实际上他都是零了。有人来说他这样一个鱼像究竟长什么样子?你这个鱼像原来 这个 r n x, 他是谁的无穷小量啊?是 x 减 x 啊, n 减一啊, n 节的这样一个无穷小量。那如果你对人家进行了一次求导以后,我就写成这样一个符号了啊,那不就你看上边求导的话,括号里头求导谁都会吧,那不就变成了 x x 减 x 零, n 减一接这样一个无穷小了嘛,对吧?所以后边的话,实际上都是加零,那同理可得括三,当 k 等于二的时候,说你这个 f 片片 x 零是等于二倍的 a 一的 a 二的啊,那 反过来的话,你说你这个 a 二等于多少,那不就相当于 a 二,它是等于二的阶层分支, f 片片 x 零往后推,其实道理都是一样的, 最终我们会推出来这个 a k, 它就是等于可以接成分支,可以接倒数对应的这样一个值,这不就完了吗?这就证明了这个泰勒展开的唯一性了。那接下来我们就要总结一下这个泰勒公式的好处了啊。这个泰勒公式的话,你也看到了,它可以将一些复杂的函数, 毕竟近似的表示为简单的多项式函数,你看后边他是不是一个多项式的形式啊,因为 a 零 a 一,这些都是什么?都是系数,都是长数啊。正是因为他 公式有了这样的好处,这样的优点,泰勒公式呢,这种化繁为简的功能,才使得他成为分析和研究是一个数学问题的有利工具, 那接下来我想说的就是这个麦克劳林公式了。究竟什么是麦克劳林公式呢?其实非常好说,泰勒公式里头的话,我们是在哪个点处展开的?是在 x 就是自变量 x 零这样一个确定的位置展开的,现在我们让这个 x 零等于零复制就可以了,带进去吧。那 x 减零的话,那后边就不写了, x 减零的一次方, x 减零的二次方,是不是那后边都一样了?原来啊,麦克劳林公式它实际上就是泰勒公式的一种特殊情况,是泰勒公式在 x 零等于零处的这样一个展开,就叫麦克劳林公式了。麦克劳林公式就是泰勒公式的一种特殊情 情况,指导就行。那但是我们并不能满足以上对于像 r x 的定性表述。为什么 定性表述呢?因为我们只知道他是这样一个 n 次方的无穷小,包括这个太乐定理里头,太乐公式里头也说明了他只是一个无穷小,并没有定量的来描述,能不能用一个公式来定量描述出来呢? 可以的,所以接下来我们就要介绍什么介绍这样的泰勒种植定理了。微分种植定理有有三个,他不包括泰勒种植定理,微分种植定理有什么?拉格浪日定理, 哦,还有什么罗二中指定理,还有克西中指定理。我想说的是,最后我们证明拉格朗日鱼性的时候,证明过程并不是用的拉格朗日定理,用的是克系中指定理。所以之前我们讲的克西中指定理,回去一定好好复习一下啊,那他的中指定理,他的表示是什么呀? 如果韩束 fx 在 x 零某个开区呢? a 到 b 内有 n 接一接啊,有 n 加一接的倒数,一定记住了啊,那么对于任 任意一个 x 在 ab 范围内,那此时的 fx, 你看展开的话,前头都是一样的,没有任何区别,就是泰勒展开, 那后边的话,这个 r n x 不是,不是说就是简单的这样一个无穷小就可以了,人家是定量好写出这样一个式子, 哎,这个狮子的话,我们发现这个规律还是符合的啊,只不过呢,你看,如果说他下一个写成 x 零,那 接下来是不是就符合这个规律了?但是呢,我想说的是,它里头这个科赛不是 x 零,它是介于 x 和 x 零之间的,所以呢,它这个东西叫什么?最后这个 r x, 如果你定量的这样写出来这个公式,它就成为 拉格朗日鱼香了。那如何去证明这样的泰勒种植定理呢?我想告诉你啊,如果你想证明泰勒种植定理,一定再看一遍,可惜种植定理的内容啊,上期我们都讲完了,那怎么去证明?现在就来说了啊, 这个证明过程并不简单,首先我们要构造两个函数,两个辅助函数,那另外一个辅助函数的话就是这一题,这一题的话好说,这个就很简单了, x, 注意一定要把 t 看成自变量啊, n 加一次方,那写完这个之后的话,显然我们两个函数,这两个辅助函数,因为什么?因为这个 ft 和 gt 呢?他在哪啊?在 x 零到 x 这样一个 b 区间是连续的,但是呢,这个 x 零和 x 不一定哪个大啊,或者说如果说这个 x 比较小的话,我们就应该写成 x 到 x 零这样一个 b 区间了啊,他是连续的,好 在 b 区间连续,而且在什么?在开区间。可倒吗? x 到 x 间,哦,可倒。所以说是不是由科系终止定理,所以我们直接写科系终止定理,马虎就简写了啊。那科系终止定理的内容 指的是什么?指的是我直接写与 x 之间,后边我为什么没有写成这样的区间的形式?因为我们并不知道这个 x 零和 x 哪个大哪个小啊,所以,但是这个可在肯定夹在他俩之间。 那写到这之后的话,接下来一定要注意一点。注意什么?你自己带一下,你把所有的 t 注意啊,把所有的 t 都换成 x 以后,你这个 fx 是不是等于零啊?同样的道理, 你后边你把这个字变量 t 换成 x 是不是也是零啊?所以这是零,然后这一部分也是减到的零,那后边就好说了,咱就继续来算了啊。减零后边就不说了,他是等于这个 f 片的话。哎,他怎么算?你自己来好好算一下,最难的时间也就是这一部分,求职。 嗯,多算一算,多练一练,多花点时间,肯定可以写出这样一个结果来。分母这个球导就非常容易,我就直接写了,确实非常容易,一定要注意这个内存来说, 这个 t 前头自备辆,前头带有一个副号,所以这个位置我们也加上这个副号,那最终的话一处理就变成了。所以这个 fx 零等于什么?等于你把这个这个 x 零直接写到后边去啊,那就是 n 加一接,哦,这样的接成 f n 加一接 x 键。为什么 x 键 x 零 n 加一键?因为你已经把 gx 零给移到右边去了。写成这样一个指以后带入哪?带入这样一个式子,带入第一个式子里头啊,带入了 带入这样一个式子中,最终就写出来了。所以说 frx 等于等于什么?就等于这样一个你需要求证的形式。剩下我就不多写了,这个还是有难度的。 那么最后一点的话我就说一下这样的带拉格朗日鱼巷。什么叫拉格朗日鱼巷呢?咱们看着啊,将带有拉格朗日鱼巷的他的公式刚才已经说过了,就是后边这样一个形式,他就是拉格朗日鱼巷的。我们 这什么,我们让所有的 x 零都取成零,你看 x 零等于零的时候就变成了什么泰勒公式,就变成了麦克劳令公式。 嗯,然后这个可赛的话变一下形式,但是本质是一样的。最终这个形式的话就叫什么?就成为带拉格朗日鱼像的麦克劳林展开时。那这节课你学会他的公式和麦克劳林公式了吗?分享课堂知识,感受数学之美。我是范老师,下节课再见。
7725会放羊的教书匠 05:55
05:55 02:26
02:26 14:25
14:25 00:22
00:22











