直角三角形斜边中线怎么折
粉丝154.6万获赞354.2万
相关视频
 03:01查看AI文稿AI文稿
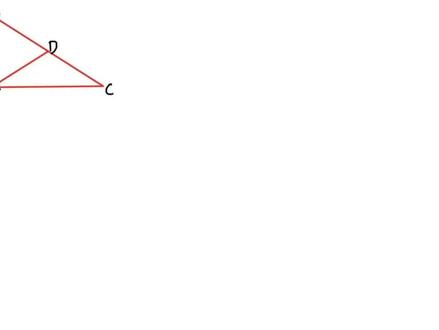
03:01查看AI文稿AI文稿如果三角形 a、 b、 c 是一个直角三角形啊,然后 a、 b 与 b、 c 垂直,并且点 d 是斜边 a、 c 的终点,也就是线段 a、 d 的长度与 ca 的长度是相等的,那这个时候,这个线段 b、 d 就叫做三角形 a、 b、 c 斜边上的中线了。 直角三角形斜边上的中线等于斜边的一半。为什么直角三角形斜边上的中线是等于斜边的一半的呢?那是因为矩形的对角线 相等且互相平分,那也就意味着 d、 a、 d、 b、 d、 c、 d、 e 四条线段全相等。既然全相等,所以我要盖住一半,只保留一个直角三角形的话,那么 d、 a、 d、 b、 d、 c 当然相等呀! 我们知道,当我们已知角 a、 b、 c 是直角点 d 又是 a、 c 的终点的时候,利用直角三角形 简便中线的性质,就可以直接得出 b、 d 等于二分之一 a、 c 也就是 b、 d、 a、 d、 c、 d 三条线全部都相等了。那么反过来,如果我们只知道 a、 b、 c 是直角,并且 b、 d 跟 c、 d 两个线段相等的话,我们能够得出这个点 d 是 a、 c 的终点吗?这个也是可以的。 由于 d、 b 跟 d、 c 的长度是相等的,那这个 d、 b、 c 肯定就是一个等腰三角形,等边对等角,那么这个 d、 b、 c 和角 c 就肯定相等了。把这两个角记作阿尔法, 那由于三角形 a、 b、 c 是一个直角三角形,所以角 a 与角 c 应该是互余的关系, a、 b、 c 是直角,那么这个角 d、 b、 c 与角 a、 b、 d 也是互余的关系。 等角的与角肯定是相等的,所以我们就可以退出这个角 a 跟角 a、 b、 d 也是相等的角,我们把它们两个记作贝塔,这样的话,等角对等边,我们就可以退出 a、 d 等于 b、 d 了,自然就能够得出 a、 d 跟 c、 d 等了。 那如果现在我们只知道 a、 d、 c、 d、 b、 d 这三条线段相等,能不能证出 a、 b、 c 是一个九十度的角呢?当然也是可以的, 当我们知道 a、 d、 b、 d、 c、 d 三条线段相等之后,那那就意味着 a、 b、 d 和 c、 b、 d 是两个等腰三角形, 等边对等角,那我们还是把这两个角记作阿尔法,这两个角记作贝塔三角形内角和是一百八十度,我们可以知道整个 a、 b、 c 的内角和就是两个阿尔法, 再加上两个贝塔就等于一百八,这样的话,一个阿尔法加一个贝塔,那肯定就是九十度了,也就是说角 a、 b、 c 肯定就是九十度。或者我们也可以去想,如果 d、 a、 d、 b、 d、 c 三条线段相等的话,那么这就意味着点 a、 点 b、 点 c 都在以 d 为圆心, a、 c 为直径的这样的一个圆的圆周上,而直径所对的圆周角又肯定是九十度的角,所以这样也能够推出角 a、 b、 c 是九十度。
685初中数学刘老师呀 06:25查看AI文稿AI文稿
06:25查看AI文稿AI文稿直角三角形,斜边的中线等于斜边的一半。看到这里纯文字表述的题目呢,我们首先应该根据文字表述把图形给画出来。 接着呢,我们要分三步进行书写。第一步呢,写出已知已知三角形 a、 b、 c 是一个直角三角形 c、 d 呢是斜边 a、 b 上的中线。 接着呢,把求证写出来,求证 a、 b 等于二倍的 c、 d。 这已知和求证都是我们自己要书写的。 第三步呢,当然就是我们的证明过程了,证明的是 a、 b 等于二倍的 c、 d, 实际上也就是 c、 d 等于二分之一的 a、 b。 那么这个问题该如何证明呢?要让我们证明的是 a、 b 等于二倍的 c、 d。 我们常用的方法当然是要构造出一条新的线段,是等于二倍的 cd 的。比如说,我们需要添加辅助线。 在三角形全等里面有两类添加辅助线的方法,第一种呢是节长补短,第二种呢,是背长中线。而节长补短呢,经常帮助我们解决的是线段之间的和差倍分问题 啊。背长中线呢,经常帮助我们解决的是一条线段是另外一条线段的两倍的这样的问题。 那么仔细观察一下这个图形,它告诉我们的是 c、 d 是 a、 b 上的中线。我们想当然,我们当然会想到用的是被长中线,比如说,我们不妨延长 c、 d 指 e, 使 c、 d 呢和 d e 是相 相等的,然后连接 b、 e, 当然同学们也可以连接 a、 e, 实际上方法是一样的。又说我们构造出了一条新的线,线段应该是 c、 e, 而 c、 e 呢,是等于二倍的 c、 d。 我们接下来的任务就是要证明出 c 与 a、 b 是啊,相等的,那么通过刚才的背长中线,我们能够发现有两个三角形是全等的, 他们是三角形 a、 c、 d 于三角形 b、 e、 d。 那么全等的依据是什么呢?我们来一起找一下。 c、 d 呢,是 a、 b 上的中线,我们可以得到 a、 d 呢和 d、 b 是相等的,又因为我们做的是背长中线,所以说 c、 d 和 d、 e 也是相等的,还有一 一组对顶角。那么根据 s、 a、 s, 我们能够证明出这个三角形与这个三角形是全等的。有全等我们能够得到对应边,对应角都是相等的,那么对应边就是 a、 c 和 b、 e 是相等的,我们来标注一下。 那么对应角呢?也就是说角 a、 c、 d 与角 b、 e、 d 是相等的,同时角 c、 a、 d 呢?与角 e、 b、 d 也是相等的, 我们来把这个角给标注一下。那么看到这两个角相等的时候,同学们能够得到线段 a、 c 与线段 b 之间还满足怎样的一个关系呢? 我们知道,如果两条直线被第三条直线所结的话,内错角相等,两直线应该是平行的, 又因为角 c、 a、 d 呢,与角 d、 b、 e 是相等的,我们是否可以得到线段 a、 c 与 b、 e 是相等的, 是平行的呢?当然了,内错角相等,两直线平行,比如说我们通过背长中线构造的两个三角形,他们有,他们是全等的,那么里面的线段呢?满足的是相等并且平行 好,他不仅针对的是直角三角形,实际上对于任何一个三角形都是满足的,那么有三角形全等,我们得到了对应边,对应角是相等,但是不要忘记我们的最初目的是要证明的是什么呀?我们要证明的是 c、 e 呢?与 a、 b 是相 相等的,那么要证明两条线段是相等的,我们的老方法是证明这两个条线段所在的两个三角形是全等的。那么仔细观察,我们能够发现,这两个三角形呢,应该是三角形 a、 c、 e 于三角形 e、 b、 c, 它们全等吗?我们来找找条件。 a、 c 于 b、 e 是相等的,这是我们通过三角形全等得出来的条件。那么 b、 c 呢?是一条公共边,我们还需要找到一组条件 制度条件当然是两边的夹角,也就说我们需要证明出角 a、 c、 b 呢,与角 e、 b、 c 是相等的,他们相等吗?当然是相等的,为什么呢?因为 a、 c 与 b、 e 是平行的,而 a 呢,垂直于 b、 c, 所以说我们能够得到 e、 b 同样是垂直于 b、 c 的, 也就是说角 e、 b、 c 是一个直角。既要根据 s、 a、 s, 我们能够证明出三角形 a、 c、 b 与三角形 e、 b、 c 呢, 是全等的。有全等我们当然可以得到对应的边是相等的,又是 a、 b 等于 c, 我们写一下, 而实际上 c、 e 呢,是我们构造的新的线段,它是等于二倍的 c、 d 的, 所以说我们能够得到 a、 b 是等于二倍的 c、 d 的。也就说我们将问题已经证明出来了,直角三角形斜边的中 线是等于斜边的一半的。那么这么这个题讲完之后,我们来一起总结一下题目。要让我证明的是,直角三角形斜边的中线等于斜边的一半。我们首先想到的是构造出一条新的线段,而构造的方法呢是背长中线, 通过背长中线呢,我们能够得到两个三角形是全等的,那么在全等里面,我们不仅可以得到线段是相等的这样一个数量关系,还能够得到他们之间的一个位置关系是平行的。好,这个题呢,我们就讲到这里。
4945蜗牛壳 06:25
06:25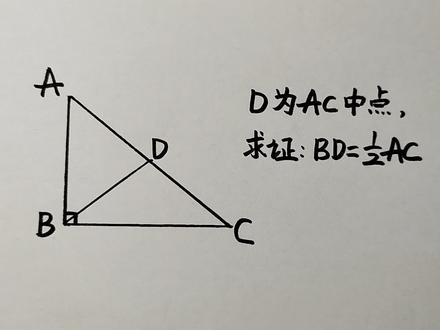 02:32查看AI文稿AI文稿
02:32查看AI文稿AI文稿大家好,来看这样一道题,三角形 a、 b、 c 是直角三角形角 a、 b、 c 是直角,那地是斜边, a、 c 上的终点啊,求正, b、 d 等于二十分之一 a、 c。 很多同学说,这还用正,这是一个定理对吧?直角三角形中,斜面上的中线是斜面的一半,确实有这样的定理,但是今天呢,我们来证明一下这个定理啊,这定理是怎么得出来的呢?呃,同学们看一下辅助线如何来做。 其实这个定理我们是在学矩形的时候啊,有这样一个定理,呃,基本做法就是先构造一下矩形,我们先来构造个矩形, 过点 a, 做一下 b、 c 平行线, 然后再给我点 c 左 a、 b 的平线,这两条平线呢,交于一点啊,假如说这是点 e, 那么这个时候, 呃, a、 b、 c、 e 啊,它就是一个矩形,对吧? a、 b、 c、 e 是矩形的话,因为 d 是终点,所以我们直接把点 d 和 e 连起来, b、 d、 e 当然是贡献的,因为 b、 b、 e 呢,是矩形的对角线, a、 c 也是矩形的另外一条对角线, 那矩形我们知道它的性质是什么?对角线平分且相等,也就是说 a、 c 等于这个 b, 而且 a、 a、 d 等于 b, d 等于 d 也等于 d, c 是不是这样?那么既然这样的话,那肯定 b、 d 既然等于 a, d 也等于 d, c 的话,那显然 b、 d 就等于 二分之一 kc 了,对吧?啊,这是一个分析过程啊,同学们可以自己把这个证明的过程写完啊,可以说非常简单,直接构造矩形,然后说明矩形对角线平分且相等,最后就可以证明这个结论。 当然呢,也正法并不唯一,是不是也可以考虑这个被偿公式来去证明一下啊?同学们可以自己去完成。
79师道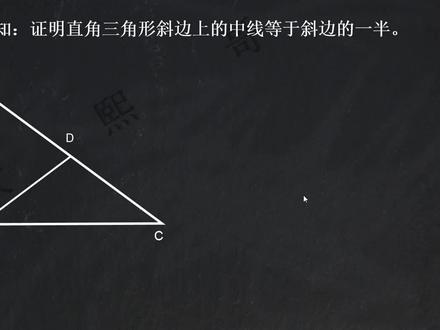 03:23查看AI文稿AI文稿
03:23查看AI文稿AI文稿大家好,我是大西哥,直角三角形斜面上的中线等于斜边的一半,这样一个性质我相信大家应该都已经是比较熟悉了,我们在解题过程中也经常会用到,其实很多体重他都能够发挥嗯比较重要的一个作用。那么大家有没有想过 我们怎么去证明这个性质,就是怎么证明我们直角三角形斜面上的中线,它的长度就是我们斜面的一半,这两天我们正好有分享到我们的背长中线法,来解决我们其中出现中线的 这一类题,那么其实要证明指甲三角形斜面上中线这一个性质的话,我们也可以用到背上中线法,按照我们背上中线法的惯掉,我们直接把我们的 bd 进行 一个延长,我们把 b d 延长到一点,使得我们的第一就等于 b d, 这样就完成了我们中线 b d 的一个延长, 并且此时我们的 ac 和 b 一是一个互相平分的关系,所以我们不妨把我们的 a 一和 c 一给连起来,我们把 a 一和 c 一进行一个连接, 那么此时由于我们的 ac 和 b 一是一个互相平分的关系,所以我们的 abc 一是不是就应该是一个平行四边形?并且由于我们三角形 abc 啊,它是一个 直角三角形,我们的角 abc 就等于九十度,所以有一个角为九十 十度的平行四边形,是不是就是一个矩形啊?那我们就可以判断我们的平行四边形 abc 他其实是一个 举行,那既然是举行的话,那么他的两条对角线应该是一个相等的关系,也是我们的 ac 和 b 一是相等的,之前我们的第一和 bd 相等,所以我们的 bd 是不是可以表达为二分之一的 b 一, 二分之一的 b 一,他就等于我们二分之一的 ac, 所以我们得到了 bd 等于二分之一的 ac, 这样呢,就可以把我们这样一个性质给证明出来了。但其实如果熟悉我们初中几何的一些证明方法的同学,我们可以想一想啊,其实如果我们 bd 大于 ad 或者小于 ad, 其实他都是不成立的。比如说当我们的 bd 大于 ad 的时候,那我们的这个角叫 abd, 肯定是要 小于我们的角 b a d, 因为我们的大边对大角小,小边对小角,同样的道理,我们的 dbc 也会小于我们的角 bcd, 那么两个角比这两个 锐角都要小,所以他们加起来肯定不可能是九十度,对吧?那这个题其实还有其他很多的证明方法, 后边我们可以来给大家一一进行一个分享。当然其实我觉得应该不用讲,这应该不是一个很难的一个知名题。好了,关了西哥了解更多解题方法,杨丽的数学思维。
545奥义大熙哥 12:3720蔡老师讲数学
12:3720蔡老师讲数学







![[初二数学]直角三角形的性质一一斜边上的中线 #每天进步一点 #涨知识 #数学思维 #学习笔记 #学习方法](https://p3-pc-sign.douyinpic.com/tos-cn-p-694b40/oQMaSW8nLOGQRWfq8GfEfbIsQpgChgSATDf7u0~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079219600&x-signature=ngKl3%2FOxwUZCfpfSH4IVt%2B45vt0%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251123093036D885A14C09E62A5EF112)




