正弦为什么要在圆中定义
粉丝19.0万获赞80.3万
相关视频
 00:20
00:20 14:39查看AI文稿AI文稿
14:39查看AI文稿AI文稿同学们,今天我们学习三角函数的定义, 主要学习第一种定义,单位元定义法,也就是用单位元来定义任意角的正弦函数,余弦函数。那么如何利用单位元来定义 三角任意角的正弦函数,余弦函数呢?首先咱们画一个直角坐标系, 在这个直角坐标系里边,以 ox 为四边, 然后做出一个角阿尔法,这然后呢,画一个单位元一 坐标轴,他的圆点为圆心半径为一的圆,咱们成为蛋为圆。 这个单位员和这个角 r 法,他的中边有一个焦点 p, 假设他的坐标是 uv, 那么我们说这个叫阿法,他的正弦散牙法就是这一点的重坐标了,而他的余弦指就是横坐标。 那么这种定义法呢,和咱们初中奖的在直角三角形中, 正弦三氧化等于 对 mp 比上斜, om 叫正弦。然后 这个初中讲的余弦口三牙法等于零比斜,这个定义是一致的,但是初中呢,咱们选直角三角形,只能对一些锐角做出这节三角函数的定义。那么对于 任意角来说,今天我们学习的任意角,那么初中的定义法显然不合要求了, 因此呢,我们就任意的做出这个角,这个角,刚才我做的是第一项线,当然也可以做出第二项线,当角 r 发在第二项线的时候, 他和单位员也有交点,这个交点坐标了,价值还是有为,那么三亚发仍然是中坐标为扣,三亚发仍然是横坐标有, 那么这个叫阿尔法洛带,第四象限,第三象限等等,不管哪个象限,这种定义呢?哎,都是符合要求的, 这是单位言的定义法,所以说呢,我们说任意角的正线函数与线函数的定义啊,也就是有如图 任意给一个叫阿法啊,咱画了一个叫阿法做一个单位员,叫阿法的中边和单位员的焦点,咱们假设是这个 uv, 那么点屁,他的 行动坐标他都是唯一确定的。我们把点批的重坐标就是这个 v 定义为叫阿发的正弦直记住微等于三阿发。而把点屁的横坐标 u 定义为叫阿发的余弦直记住,又等于扣三阿发。这就是三角函数里边单位元定一法。 那么利用单位沿定语法呢,咱们首先可以求一些特殊角的三角函数值,比如说先求三三十度, 那么第一步呢,先画一个单位元, 然后把这个三十度角画出来,假如咱画的这个角啊是三十度,那么要求上于三十度好办,咱们就只需要求出这个角的中边和单元的焦点的坐标就行了, 因为这个是单位眼,半斤是一,那所以呢,如果做出小直角三角形的话, 那么这一点的重坐标显然是二分之一,而行坐标根据勾固定理可以求出这个 om, 他就是二分之根号三, 因此呢,这个点 p, 他的行坐标是二分之二,三中坐标是二分之一。这样呢, 我们就看出三以三十度就等于二分之一,就要总坐标这一点的总坐标,而后三以三十度呢,就要这一点的横坐标,所以呢,就是二分之一二三。 当然,如果球散一百三十五度怎么办呢?好,还是做出这个一百三十五度,一百三十五度不就是这个九十加四十五吗? 做出这个一百三十五度之后,还是啊把这个焦点的坐标求出来,那么这个球呢,由于他的 这个画一个小字叫三角形,他的斜边是一,那么我们求这一点的坐标,这点坐标怎么求呢?咱们得 学过小直角三角形里边,如果鞋边是一,他是一个四十五度,是一个等边,他是一个等腰直角三角形设两个指甲边。 如果这个 om 是 x, 那么 mn 呢?也是 x, 这样一来,高估定理, x 方加 x 方等于一, 所以二 x 方等于一,这样一来, x 方等于二分之一,所以 x 呢,就等于二分之,不靠二,当然正负两个,咱们这个呢,作为三角形边长来说,咱们光要正的二分之高二, 那这样一来啊,这个点的坐标行坐标是二分之高啊,所以是后的二分之高啊。动坐标因为在第二项 线,所以是二分之高啊,是真的,那这样一来啊,这个一百三十五度,他的 要重坐标二分之根号啊,口散一百三十五度呢,就要横坐标负的二分之根号啊。 那么咱们要是求口才一百八怎么办呢?好,那同样一百八十度,这个角的中间不就是 x 轴的副班轴了吗?然后找出他和单位员的焦点,横坐标是负一, 重坐标是零啊,咱们鱼险是要横坐标的,所以口算一百八十度呢,他就知道。 那么这个呢,就是利用单位眼定义法九三角函数值的这个方法,关键就是找这个特殊角, 他的角的中边和单位圆焦点的坐标,只要坐标求出来了,横坐标就是这个角的 余弦了,而重坐标就是这个角的正弦了,这就是这个利用单位元定义法。哎,我们求特殊角的三角横竖直的这个方法, 那么我们呢,还可以利用单位元定义法,确定各项线的这个三角函数值的正负,好画一个单位元, 在第一项线的时候,由于脚的中边和单位原交点的这个横中坐标全为正直,所以说在第一项线, 当阿发为一象线的时候,哎,我们说正弦三,阿发大于零,余弦也是大于零的阿。阿发为二象线时, 二相线的时候,由于这个角他的中边和单位原交点的横中坐标,这时候行坐标就小于零了,重坐标大于零,有小于零, v 大于零。那这样一来呢,我们说在第二项线,正弦是正的, 而余弦呢,他就是负的。那同理,阿发为第三象线的时候, 第三项线我们说由于横动坐标都是负的,所以散阿法小于零,口散阿法小于零,那么到了阿法为四项线 事项现实这时候,由于横坐标是正的,重坐标是负的,所以散阿发小于零,口散阿发大于零。那么经过 这个总结,我们发现在第一项线的时候,全部是正的,所以咱们记的时候就是一全正,一全正,三角函数都是正的。 在第一项线,第二项线呢,你发现正弦是正的,所以二正弦二项线,正弦是正的。第三项线呢,我们说三小于零,头三小于零,但他的正切摊着拿法, 他是三除一口三,所以第三项线呢,正切是正的, 所以我们称为三正切。而第四相信鱼弦是正的,所以是鱼弦。 因此呢,咱们记三角函数值正负的时候,根据 这一个角的中边和单位沿焦点的横字坐标的正负,可以得到一全正、二正弦,三正切 事与线。那么最后呢,咱们再学习一下利用单位元定义法解三角不等式。那么利用单位元定义法呢,可以解简单的三角不等式,比如说我解三 f 大于的二分之一,好换一个单位元, 然后再画一个 y 等于二分之一,大于等于二分之一,那么就是重坐标在二分之一上边的这些点, 这些点所对应的角膜,我们就要这个角,因此呢,先找 这个临界的特殊角,我们说三十三十度,他是二分之一,那么对称着三 一百五十度,这个一百五十度也是二分之一,那要想晒阿方 大于等于二分之一,那这个角的中边和单位沿的焦点呢,只能落在这一段弧 a 到 b 这一段列弧上, 那因此呢,他所对应的最后的结果啊,法就应该是大于等于三十度,加上 k 乘三百六,而小于等于一百五十度,加上 k 乘三百六。 然后呢把这个写成集合的形式, k 属于 z, 那么这 一个结果我们说呢,就是利用三角里边的单位元定义法, 然后呢接这个三角不等式。将来我们学习了这个正于弦函数的图像以后,还可以用图像法接这种三角不等式啊,不过作为单位员定义法的应用哎,这个呢,也可以好好的理解一下。 那么今天呢,咱们主要是哎通过单语言定义法,咱们研究了三个内容啊,就是第一,第一个内容, 我们说可以求一些特殊值啊,可以求一些这个特殊角的三角函数值,利用单位元定义法,哎,求这些特殊角的三角函值。第二呢,哎,我们可以利用 单元定义法来确定这个各项线正弦于弦正切的这个符号问题。最后总结出一个口诀,一拳正而正弦三正切是于弦。 最后是利用单位元定义法解简单的三角部等式,通过画图,最后呢,找出满足 这个大于等于二分之一的三亚发。三亚发主要是看重坐标的,因此呢,咱们 就是找脚中边的时候,就是看哪些点的重坐标位 比这个二分之一大,只要大于二分之一,这个这个列弧上的点, 将来他的重度要高大于二分之一,因此呢,对应的角应该比三十度大,而比一百五十度小,因此呢,介于三十度和一百五十度之间,最后再加上周期就行了。 好,同学们呢,这个当然定法咱就说到这。
153数学老张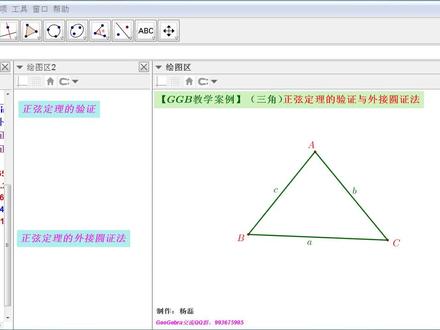 06:57查看AI文稿AI文稿
06:57查看AI文稿AI文稿嗨,大家好,今天我们分享一个 ggb 教学案例,在三角函数当中的正弦定理的验证与外结缘正法, 我们可以做出这样的效果,可以拖动三角形的三个顶点,从而改变三角形的形状。我们可以用 ggb 来对正弦定理进行验证, 可以通过 ggb 当中的计算得到 a 比上三 a 等于 b 比上三 a, c 等于 c 比上三 a, c。 当三角形形状改变的时候,那这个定理仍然是成立的, 我们可以构造正弦定理的外圈圆正法, 在这个构造当中,我们采取的是外结圆的圆心角,是圆周角的两倍, 从而我们可以得到 a 比上一个三 a 就等于二啊, 在这里就是十点三。好,下面我们开始制作, 我们先将之前制作的内容全部删除掉, 我们先用多边形工具构造一个三角形 abc, 构造的过程当中,他会默认这个三角形的三个边分别就是小 a, 小 b, 小 c, 那如果我们要对他进行验证的话,在这里我们使用文本,用文本工具 创建一个文本,选用雷太公式, 那在这里是 a 比上三移,我们引用 这样的一个分式公式, a 比上三 a 等于 仍然是一个分式,那这个 a 我们希望他是一个具体的值,这时候我们可以点击对象,引用里面的小 a 这个对象, 这里的 b 是 sign, 在引用对象是 角 a, 但是这里的角 a 呢?在我们的带数据当中,并没有单独的把它列出来,所以在这里我们先确定了之后啊, 在指令框当中输入一个指令叫角度, 我们直接几个对象就是三角形 t, 一确定,这时候这个三角形的三个角度就全部出来了, 我们可以打开这个角度的属性,将样式里面的大小设置一下,可以标签去掉,然后再打开刚才的文本, 在这后面输入一个二法,在这里面找对象,里面找到二法,这个角度。好,这个 可以在预览里面看到我们这个文本所呈现的效果,然后他就等于引用一个空白公式框 a 除以 sign, 这个是二发, 二发这个符号我们可以用符号常规里面有个二发。好,确定好,这时我们可以看到有一个这个公式框啊,这个文本啊,这个文本呢,我们也就做好了啊, 我们可以修改一下文本的底色,字体颜色等等, 那类似的呢,其他的两个文本也是一样的啊,在这里我们就不再制作啊,大家 自己制作一下就可以了啊。之后呢我们做三角形的外接圆,那这个外接圆我们直接使用圆的工具,外接圆工具 他是选定不同不在同一直线上的三个点也在这里,就是选择 abc 三个点,这样就出来一个原地, 然后再用中心工具得到外结缘的中心,我们可以对他重新命名一下,命名为欧典, 之后再用垂线工具过欧点做边 a 的垂线,再用焦点工具得到这个垂足, 隐藏刚才的垂线, 之后用线段工具连接 oboc, 再用多边形工具连接 obd, 这样构成一个多边形,我们可以把这里面的几个标签去掉, 改变一下三角形的颜色。 好,这样呢,我们这个案例呢,大体上就做好了啊,当然如果你 需要对他进行一些美化,就是一开始啊我呈现的那个样子的话,那你在做其他的一些美化的操作,那这个案例呢?基本上就做好了。好,我们的分享呢,就到这里,感谢聆听,再见。
47享玩数学
猜你喜欢
- 2496以父之名
















