上期呢,咱们介绍了古人求圆周率派的一些算法啊,无非就是割圆做这个正独白行,然后呢,一点一点的去逼近啊,这都算是几何思路。等到了中世纪啊,极限和微积分的思想发展出来之后啊,一些派的新算法就出现了。 那么这一期呢,咱们就来简要的介绍一下派的无穷项算法啊,哎,各位不用感觉很难啊,至于繁琐的推倒过程啊,我尽量的省略还是老惯例,咱们重点啊,就分析一下前人的这个思考过程和灵感来源啊,这个是最主要的啊。 好了,进入正题。在欧洲啊,第一个给出派的无穷项公式的人,那是法国的数学家伟达,就是提出这个伟达定理。那位伟达在一五九三年啊,他就给出了这样一个公式啊,这是一个无穷成绩公式啊,他还不是无穷极速呢。呃,所谓无穷极速,就是指 一组无穷狩猎他的和,对吧,他这是成绩,但是他这个公式啊,可以说是第一个关于派的有限和无限之间的桥梁啊。下面啊,咱们就来看一下伟达的想法。首先伟达呢,也是从个圆开始啊,呃,这是一个圆,然后呢,我们做一个内接正方形, 我们假设这个圆,他的半径呢,等于一,那么圆的面积就等于派,对吧,那正方形的面积是多少呢?边是根号二,那正方形的面积就是二, 如果按照古人的思路,那就得继续分割说,我做正八边形啊,正十六边形等等,然后一点一点的去算这个面积,去逼近 伟达呢,是这样想的,假设我们用这个正方形的面积比上这个圆的面积,也就是二比上派, 那他应该等于多少呢?如果我们可以继续分割正多边形,那么这个圆的面积就应该等于一个边数为无穷大的一个正多边形,他的面积,对吧?可是乍一看啊,这这句话就等于没说啊,不过伟达说,没关系啊,我把这个柿子呀,给他加一些象进去, 加什么呢?我让这个正方形的面积啊,先比上一个正八面形的面积,然后呢,再乘以一个正八边形的面积,再比上一个正十六边形的面积, 再乘一个正十六边形的面积,比上正三十二边形的面积。这么以此类推,你这样一直写下去,最终就是某个正多边形,他的面积,然后呢,比上一个这个 s 正无穷大,其中我每两项都可以约掉啊,所以整体这个式子一定是相等的。那下面啊,咱们就得期待 一件事了,就是如果这个无穷成绩的每一项之间,他存在着某些规律,哎,那就完美了啊,有没有这个规律呢?有啊,我先直接把这几个呃正多元形的面积公式告诉大家。 这个正八边形,他的面积呢,就是二倍的根号二,然后再乘以一个二方啊,其中这个二就是外地元的半径,咱们举这个例子就等于一对吧,正十六面形,他的面积呢,是四倍的根号下二,减去根号二,再乘以个二方。 正三十二变形,它的面积呢,就是八倍的根号下二,减去根号下二,加上一个根号二,再乘以个二方,这几项就足够了啊,我把每一项带入,然后呢再化减一下,那这第一项就是根号二比上二,这第二项呢, 就是根号下二,加上根号二比上二,第三项就是根号下二,加上根号下二,加上根号二比上二。 发现规律了吧?这样我求前几项的面积就够了,我之后一直写就可以了啊。但是伟达是有严格证明的啊,这前边是二比上派,这个公式就叫做伟达的派公式, 他也可以求这个派的近四指,因为你越往后,这个每一项啊,他就越趋近于一,所以我们可以从其中的这一项给他去截断,然后去估算这个派指。那说这些个面积公式,这是怎么来的呢? 是这样,我们画一个圆,然后呢,假设这是正多边形的一部分,假设这个圆的半径呢是 r, 那正多边形的面积就应该等于这个三角形的面积,再乘以一个相 相应的边数,对吧?那这个三角形的面积等于多少呢?半底乘以高呗。我们就假设这是一个正 n 边形,那这个大角就是二派比上 n, 他的一半,这个角就是 pad 比上 n, 然后我们用这个 r 来表示底和高,这高呢,就等于 r 倍的抠 siri, 然后派比上 n, 这底的一半呢,就等于 r 乘以个 siri, 派比上。恩, 所以整体这个大三角形的面积就 s, 三角形就等于 r 的平方,然后塞音派比上 n, 再乘以个扣。塞音派比上 n, 那正多边形的面积是多少呢?一共分隔成了 n 份,就再乘以个 n 就行了呗。啊,或者呢,我们可以用二倍角公式把它写成二分之 n 倍的塞音二派比上 n, 再乘以个二方 正八、正十六,正三十二正二的 n 次方边形的面积公式就可以通过这个二倍角公式不停的迭代得到了啊,这块咱们就不展开了,不过啊,咱们看这里,这个式子呀,当 n 趋近于无穷大的时候啊,他应该等于什么呢? 当恩区无穷大的时候,他的几何意义?就是咱们刚才说的就是我在这个园内画了一个正无穷边形,哎,就是这个正无穷边形,他的面积对吧? 那显然他的面积应该等于圆的面积,所以当 n 区域无穷大的时候,这个式子应该等于派 r 方,我们把 r 方约掉,也就是当 n 趋于无穷大的时候,二 n 倍的赛因二派比上 n, 他就等于派。 咱们再写个一般点的式子,这个二呢,也不要了,当 n 趋于无穷大的时候, n 倍的在派比上 n, 他就等于派。 这个式子呀,有什么用呢?至少我们可以通过计算器来求派置,你比如说我选取说,当 n 等于一万的时候,那么一万倍的塞音一百八十比上一万, 哎,你们可以通过计算器来算一下啊,他约等于三点一四一五九二六,同样可以达到小数点的七位经络啊,你恩值越大,经度就越高。其实这个极限啊, 还有更一般的同事,那就是当 n 去无穷大的时候, n 倍的赛因 x 比上 n, 他呢要等于 x 啊,不仅限于判啊,这块这个大家了解一下就行了。 好,那咱们收回到伟达公式啊,伟达公式啊,虽然开了个好头啊,不过想要层层的开根号,那在当时也不是一件容易的事啊。但是伟达的这个公式呢,却为数学家呀,就开辟了一个新思路,哎,就居然还可以这么玩。 于是呢,很快在一六五五年啊,英国数学家沃利斯就给出了沃利斯成绩。 物理寺说呀,这个派比上二,他呢要等于二比上一,然后乘以一个二比上三,然后再乘以一个四比上三,再乘以一个四比上五, 再乘以个六比上五,再乘以个六比上七。哎,这么以此类推,你看,这又是一个无限成绩。 这个公式怎么来的呢?呃,咱们不给这个具体证明了啊,咱们来说一下当时的思路,哎,我去,这个思路呢,是这样的,我们呢构造一个函数啊,是 c x 比上 x 这个函数啊,当他等于零的时候啊,这个方程的根都是什么呢?是不是就当这个 x 取 n 派的时候啊,其中这个 n 呢,要等于正负一,然后呢,正负二,正负三等等。那你看啊,我这么写, 我说塞印 x 比上 x, 他呢就等于一减去 x 比上派,再乘一个一,加上 x 比上派,再乘以一个 一减去 x 比上二派,再乘以个一,加上 x 比上二派第二点点。哎,就类似于这个音式分解一样,就是我把所有的这个根啊,都给他写出来, 那这两个式子是不是相等的呢?啊?是相等啊,如果咱们没给出这个证明啊,完全是猜想,不过没关系啊,你大胆猜想,小心求证呗。 那你看啊,当这个 x 它等于二派的时候,这个式子等于啥呢?这左边就变成了二比上派了,对吧?右边呢,就变成了二分之一啊, 乘以二分之三,再乘以四分之三,再乘以四分之五点点点, 我们把它整体倒过来,是不是就是这个沃利斯乘机啊?哎,妙吧。但是啊,这沃利斯是不是这么想的?这个 来确定啊,不过有一个人确实是这么想的,哎,这位就是欧拉,那欧拉怎么想到这呢?哎,这啊,咱们得从巴塞尔问题说起, 话说在一六四四年啊,意大利的设计家叫蒙格利,他呢就面向社会啊,就提出了一个问题啊,他问 说一的平方分之一加上二的平方分之一,加上三的平方分之一,哎,加上四的平方分之一,这么一直加,这个结果等于多少呢?哎,这个问题就叫做巴塞尔问题, 在当时蒙格利证明了,说,一分之一啊,加上二分之一,加上三分之一,加上四分之一,这么一直加,他的结果是发散的 啊,这个咱们之前说过对吧,他叫做调和级数。可是这个巴塞尔问题呢,蒙格利啊,就没想明白啊,并且在之后是一直困扰了人们一百年 颜值酒,直到一七三五年啊,巴塞尔问题被欧拉解决了,欧拉最初的想法其实很简单,他手里边呢,有两个关于正弦函数的公式,一个就是咱们刚才写的就这个狮子, 与此同时,第二个公式啊,就是这个正弦函数的泰勒展开式啊,这块咱们之前也说过啊,我直接把公式告诉大家,说呢,赛引 x, 它等于 x 减去,然后 x 的立方比上三的阶层 加上 x 的五次方,比上五的结成减去 x 的七次方,比上七的结成加上点点点。我们把右边提取出一个 x 除到左边来, 那右边呢,就变成了一减去 x 的平方,然后比上三的结成加上呢 x 的四次方,比上五的结成减去 x 的六次方,比上七的结成加上点点点,这等式左边刚好就和这个式子相等了,对吧?那好,咱们再来看这个式子。 先来继续算一步,我把每两项啊给他乘起来,那就变成了一减去 x 的平方,然后呢,派的平方, 他乘以个一减去 x 的平方,再乘以个四倍的 pad 平方,再乘以个一减去 x 的平方,再出一个九倍的 pad 平方,点着点, 然后怎么办呢?这展开了,这明显有无穷多项啊,也没关系,我们想办法把其中的二次项单独给他提取出来啊,你会发现啊,如果要想保留这个二次项,他一定是这些项啊,和这个一相成了,所以呢,这个二次项的系数呢,就应该是 负的派方分之一加上四倍的派方分之一,加上九倍的派方分之一加上点点点,对吧?那我再把这个派方给他提取出来, 就是负的派方分之一。这括号里边应该是啥呀?是不就是一的平方分之一加上二的平方分之一加上三的平方分之一。这么一直加呀,是不就是巴塞尔问题的这个无穷极数啊?哎,有点眉目了吧, 那这个二次项系数之和整体等于多少呢?哎,我们再看这个泰勒展开的这个式啊,这里边就是一个这个二次项啊, 而且呢,这个系数是负的三的阶层分之一,也就是负的六分之一啊。欧拉又说了一句,欧了啊,所以呢, 我们让这两个二次系数的这个式子呢,让他相等,也就是他等于负的六分之一,把负号一约掉,这个派方呢,给他移过来,所以这个巴塞尔问题啊,就等于六分之派方, 你看,这就是数学家的直觉啊,有的时候就是遇到难题啊,不妨换个思路啊,就是先找结论,如果验证没毛病,你再去求证啊。欧拉是一七三五年啊,得到了这个六分之派方的这个结果, 六年之后,一七四一年才给出了完整的证明。至此,巴塞尔问题啊,才完美的解决了。我们呢,也得到了另外一个关于派的无穷技术的算法。哎,这个就是一个无穷技术了啊,唯独呢,他是一个关于派方的无穷技术。那直接关于派的无穷技术都有哪些呢?
粉丝76.4万获赞504.0万
相关视频
 08:19
08:19 00:49查看AI文稿AI文稿
00:49查看AI文稿AI文稿数学上有哪些丑陋的公式?二,圆周率篇拉玛瑙金圆周率公式楚德诺夫斯基算法 我不老算法最后来个简单的只有加减法准备好了吗?他来喽!
2.7万猪猪小百科 19:29查看AI文稿AI文稿
19:29查看AI文稿AI文稿同学们,上课之前请准备好剪刀、尺子、毛线或者绳子自备本,还有几个大小不同的圆形纸片 准备好了吗?今天这节课,我们继续走进圆的世界。通过前面的学习,你已经了解了圆的哪些知识呢?是的,我们知道了圆的各部分名称,还探索了圆的特征。 关于圆,你还想进一步知道些什么呢?有的同学对圆的周长感兴趣,有的同学想知道圆的面积, 今天我们先来研究圆的周长。那么关于圆的周长,你又想知道些什么呢?什么是圆的周长? 圆的周长和什么有关?怎样求圆的周长等等。下面我们就围绕这三个问题展开学习。什么是圆的周长呢?请你在圆形纸片上指一指,说一说。 是的,围成圆的这条曲线的长度就是圆的周长。我们知道长方形的周长和他的长宽有关,正方形的周长和他的边长有关,那么 圆的周长和他的什么有关呢?哦,半径,也就是和直径有关,这种感觉准不准呢? 我们借助大小不同的车轮来研究这个问题。这三个车轮的直径分别是,二十六英寸、二十四英寸、二十二英寸。 什么是英寸呢?英寸和长度单位厘米之间又有什么关系呢? 我们一起来了解。英寸是音质长度单位。在生活中,人们习惯用英寸做单位来表示自行车车轮的规格,比如二十六英寸约 等于六十六厘米,二十四英寸约等于六十一厘米,二十二英寸约等于五十六厘米。 如果把这个三个车轮分别滚动一周,想一想哪个车轮行驶的路程最长呢?一起来看 一号车轮滚动一周行驶的路程最长。车轮滚动一周行驶的路程就是什么呢? 对呀,就是车轮的周长,车轮是圆形的,所以圆的周长和直径有关系吗? 对呀,直径越短,圆的周长越短,直径越长,圆的周长就越长。我们的感觉很准,圆的周长确实和他的直径有关, 他们之间有怎样更具体的关系呢?我们进一步借助学过的图形来展开研究。 这是正方形,在正方形里画最大的圆,正方形的周长是圆直径的几倍呢? 圆里再画一个正六边形,正六边形的周长又是圆直径的几倍呢?比一比圆正方形正六边形的周长小, 你想圆的周长大约是纸巾的几倍呢? 有想法了吗?我们一起来看。正方形的边长就是圆的直径,所以正方形的周长是圆直径的四倍, 这六边形的边长就是圆的半径。六条边长就相当于三条直径,所以正六边形的周长是圆直径的三倍。 圆的周长小于正方形的周长大于正六边形的周长,所以圆的周长比直径的四倍少,比直径的三倍 多,那我们就可以说圆的周长是直径的三倍多一点。三倍多多少呢?要解决这个问题,还需要用数据来说话, 我们可以先量出圆的周长直径,然后用周长除以直径,求出周长是直径的几倍。 那么怎样来测量圆的周长呢?用直尺能直接量出来吗?对呀,不行,因为圆是曲线图形。那怎么办呢? 有的同学想到了用圆形纸片紧贴的直尺滚动一周, 像这样是吗?为了使测量的结果尽可能的精确,想一想操作的时候要注意些什么呢? 对呀,我们要先做好记号,正好滚一周,滚动时原片要紧贴着直尺, 像这种方法,我们叫它滚动法。还有的同学想到了绕线法是怎么回事呢? 用绳子正好绕圆片一周,再拉直了测量,这就是绕线法。用这种方法测量的时候又要注意些什么呢? 对呀,绳子围紧,正好绕一圈,测量时绳子要拉直了, 我们来比一比。这两种方法虽然操作不同,但是他们有相同的地方吗?是的,他们都是把圆一周曲线的长度转化成了直直的线段的 长度在数学上叫做画曲为直。下面就请同学们拿出课前准备好的圆形纸片,请你先量出他们的直径, 再选择一种方法测量出周长,然后用周长除以直径求出商除不尽的结果,保留两位小数开始吧。 好了吗?这是老师搜集的一些数据,仔细观察, 你发现了什么?对呀,通过测量和计算,我们进一步发现了圆的周长都是直径的三倍多一些。 其实圆的周长除以直径的商,他是一个固定不变的数,他叫圆周率,可以用这个字母表示,读作太。 那为什么大家得出的结果各不相同呢?是的,在测量的过程中,或多或少会有一些误差, 虽然有误差,但是我们算出的结果和正确的结果比已经非常非常接近了。这个神奇的派到底是多少呢?一起来看这一段。 圆周率是个无理数,人们知道他约等于三点一四,我们都是使用三点一四来进行计算的,但是这个数字的来历并不简单,从古代开始,全世界的科学家和数学家都对圆周率有着痴迷的程度, 试图去把圆周率完整的算出来。我们国家的学者也不例外,并且在不断探索的过程中有所成就。 那么组充值的圆周率是怎么计算出来的呢?人类早在青铜时代已经开始对圆周率的测算了, 西方著名的科学家阿吉米德和托勒蜜都曾经探讨过这个问题,但是他们的成就仅仅只是把圆周率算到后四五位左右。让科学家们望而却步的是,后面需要庞大的计算量才能完成。而 我们中国人很早就发现圆周率可以用歌元术来求解。所谓歌元术,就是在一个言行中画出各种内接正多边形, 当边数越多时,这个多边形就会无限接近于圆形。然后人们通过计算正多边形来推算出圆周率。相传组冲织算出了正一万二千二百八十八边形。用这种简单粗暴的算法把圆周率往后推倒七位, 并且在此后的近千年的时间里,都没有人能够打破这项记录。我国之所以有这么厉害的数学成就,离不开祖冲之的辛勤努力。 原来派是个无限不循环,小数在计算时一般保留两位,小数取近四指约等于 三点一四。现在你知道圆周率派表示什么意思了吗?对呀,他是圆的周长除以直径所得的商,圆的周长总是之间的派倍。根据这三个数量之间的关系,怎样来求圆的周长呢? 圆的周长等于直径乘圆周率。如果我们用大写的字母 c 表示圆的周长, d 来表示直径,那么圆的周长的字母公式可以这样来表示, c 等于派 d。 已知圆的周长就能求出圆的直径。现在你能来求出刚才三个车轮的周长吗?试试看 好了吗?我们一起来校对。 根据 c 等于派的第一个车轮的周长可以用三点一四乘六十六等于二百零七点二四厘米。 第二个车轮的周长用三点一四乘六十一等于一百九十一点五四厘米。第三个车轮的周长用三点一四乘五十六等于一百七十五点八四厘米。你都做对了吗? 以支圆的直径求圆的周长,只要用直径呈圆周率 派,那么如果已知圆的半径能求圆的周长吗?对呀,已知半径可以先求出直径 d 等于二二,这样 c 就等于派乘二二,也就是二派二。 想一想,圆的周长是半径的几倍呢?对呀, up high 倍。现在你能来解决这个问题了吗?已知什么求什么? 是的,已知圆的半径是十四米,求他的周长。想 c 等于二派二,用二乘三点一四乘十四 等于六点二八乘十四等于八十七点九二米 要求圆的周长。只要知道什么呢?对呀,已知圆的半径或者直径都能求出圆的周长。 好,我们来回顾一下刚才的学习过程,围绕这三个问题,我们展开了研究,不仅知道了什么是圆的周长, 还通过观察比较发现圆的周长都是直径的三倍多一些,并通过进一步的测量计算得出圆的周长总是直径的派倍,从而推导出了圆的周长计算公式, c 等于派 d, 或者 c 等于二派二。下面我们就进入巩固应用阶段,你能求出下面这些圆的周长吗?试试看 好了吗?我们一起来看。从图中可以知道,第一个圆的直径是五厘米, 小 c 等于派 d, 用三点一四乘五等于十五点七厘米。 第二个圆的半径是二米,想 c 等于二派二,用二乘三点一,四乘二等于十二点五六米。那么看到这里的 d 等于三点五分, 你想到了哪个公式呢?对呀, c 等于派 d, 是这样做的吗?看到二等于一点二厘米,又想到了哪个公式呢? c 等于二派二,你都做对了吗? 摩天轮你见过吗?我们一起来看这组信息, 在摩天轮旋转的过程中,你看到了什么?对,圆 坐着摩天轮旋转一周,他在空中转过的米数就是圆的周长。所以这道题目已知什么 求什么,怎样列式呢?是的,已知圆的半径求圆的周长。想 c 等于二派二,用二乘三点一,四乘十 等于六点二,八乘十等于六十二点八米。类似这样的问题,你还在生活中见过吗?对呀,分针或者时针在中面上旋转, 如果桌面上这个分针的长八厘米,它旋转一周,针尖走过了多少厘米? 这时候针尖走过的路程指的是什么呢?分针的长又 指的是什么?对呀,针尖走过的路程就是圆的周长, 分针的长就是圆的半径,已知半径求圆的周长。想 c 等于二派二,用二乘三点一、四乘八,结果是五十点二四厘米, 我们来比一比,这两个问题有什么相同的地方吗?对呀,他们都是点动成圆,已知半径求周长,小 c 等于二派二。 好,同学们,通过今天这节课的学习,你有哪些收获呢? 是的,我们从问题开始,通过猜想、观察、比较、测量、计算,认识了圆周率,并推导出了圆的周长计算公式,还解决了一些实际问题。 有两只小蚂蚁也来到了我们的课堂中,一起来看。蚂蚁甲从 a 点出发,沿着大圆的圆周爬一圈,回到了 a 点。 蚂蚁蚁也从 a 点出发,沿着小圆的圆周爬一圈,回到 a 点。如果两只蚂蚁是同时出发的,并且速度相同,哪一只蚂蚁先回 回到 a 点呢?你觉得哪只蚂蚁先回到 a 点呢?有的同学说蚂蚁甲,有的同学说蚂蚁蚁,也有的同学认为同时到达,答案是同时到达,这是怎么回事呢?我们一起来看。 蚂蚁甲爬过的路程就是这个大圆的周长,如果大圆的直径是地,那么它的周长就是太低。蚂蚁蚁爬过的路程就是两个小圆周长的河。 如果两个小圆的直径分别用第一、第二来表示,那么他们周长的和就是派第一加派第二, 也就是派第一加第二的和,就是派的他们拔过的路程一样长,所以同时到达。好了,同学们,今天这节课我们就上到这,再见!
30扬州小虾米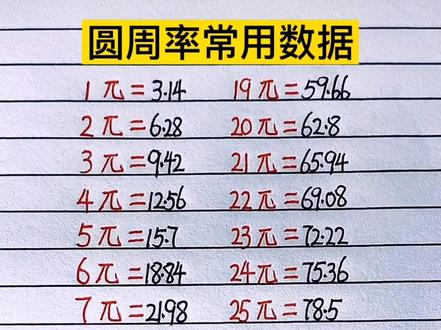 00:09查看AI文稿AI文稿
00:09查看AI文稿AI文稿给大家分享数学重要知识点,圆周率的常用数据,宝妈给你家宝宝收藏起来,带着你家孩子也来读一读记一记吧!
1506豆豆老师 01:18查看AI文稿AI文稿
01:18查看AI文稿AI文稿如何快准狠的计算圆周率呢?提到计算圆周率,大家最先想到的一定是这位老爷子。他利用刘辉的个圆数,将圆周率精确到小数点后第七位,并在计算圆周率吉尼斯世界纪录上霸榜一千多年。虽然 靠增加边数逼近圆周率的算法效率极低,但是在刘辉的三国时代,已经称得上是外星黑科技。遗憾的是,现在看来,这个方法既不快也不狠,就是挺准的。那么,到底怎样才能光速计算圆周率呢?可以出出来吗?答案当然是可以出出来! 没错,就是用这坨公式看和右边这一坨一项,就可以用一个除法搞定圆周率。不过,别高兴的太早,在这一个除法之前,你还得做无数次加法。看到这个符号了吗?他的意思是,后面这一坨东西,在 k 等于零的时候算一遍,等于一的时候再算一遍,一直算无数遍,再把这无数遍的结果加起来。不过,各位也 不需要算无数遍,这是只算一遍 k 等于零的结果。你会发现,这个记录已经快要干三次充值了。这个公式神奇的地方在于,你每勾算一项,就会得到八位圆周率的有效数字,而 元素的有效数字获取速度会随着边数增加越来越慢。这时候你是不是很好奇,这么牛掰的公式拉马努金是怎么推倒出来的?据他本人所说,这个公式是女神的马吉利告诉他的。
2.5万猪猪小百科 03:34查看AI文稿AI文稿
03:34查看AI文稿AI文稿matima tikita intian 母婴 beau humberfugumba woo 浅白的拖拉在眼里数学中很重要的一种概念。圆周率 圆周率 mc 前边突然喝的给你们前边突然喝的给你们前边 yanee put chamber ninky 中心点 cnin chamber america z air chamber american ziammd chamber americanston chamber eustein chambert americans leetubo are looking here this radio stames yani penjin dames pony order the order per cliff podium sir i'm there chamber uzudan chamber american youtube yandelbert chamberd eustrogetable are look all that chamber the armor table over there chamberland d amateurable to bunny base the arab alabamatimaticata i'm there pears macelinang bishop cassie yani chamber truck k yani 圆周绿的颜色的你们第一次 put chamber nicki eh yes sharing engage i love moose to look at yaki yes d yes sharing diameter version make a conjuniction tired version vague conjugation tire to the person are that there chamber ninquere i love moose looking in this chamber no diameter of booth's sake ooh shy shorthand you're scared madam but combat gear simmons oh boss mom buy up is that what? 看前排的除了黑眼睛,皮不?那不是皮而黑不得用不皮能看不见,除了不搞的人 对你说我得不了的对你说我得不。五位数眼里无限循环巧数 put check session rambler double ontoodland candy check session humble lodot check sesatoreland dab on again leaking toronto committee you should to use the on tool polidar to start to use the on tool polidar 布莫得莫得格的格,数学中很重要的数学概念。圆周率 to use on that and say boom chamber ninky 哎,不是 queen men 看那个 supply ms yenny champion queet me other types e, c, p, r, g fox say champagnu equity me other thrust comment 圆周率 pear no cupid tip reduce no quality rather than all of them yin it chamberlain key i'm sure using a subtle formula as well today pay or not paying fancy yander but he's up soda s 等于 p 除以二括号的平方我都得不美颜的白横全白的给 i'm using this supplies 面积新的 a supplement for 我都在读书了。
237阿老师 05:23查看AI文稿AI文稿
05:23查看AI文稿AI文稿前段时间的新闻啊,说是谷歌云把圆周率算到了一百万一位,作为一个合格的理工男,当然也想自己算一下啊,不耐创业未半而花光预算,还只好搞了个最简单的乞丐版实验, 用弹珠小球做了个蒙特卡洛模拟的实验啊,然后呢,再利用几何概型的知识来求的圆周率,结果是三点二四九, 误差大概是百分之三点四。后面我又用编程把这个实验模拟了一遍,精度更高了。但是计算圆周率不是今天的重点啊,今天的重点是讲讲我们是如何从数学理论到算法表达再到代码实现的。视频后面有惊喜哦, 要求圆周率根据圆的面积公式,可以先测量出圆的面积,然后再出一半径的平方啊,就可以得到派了。那么如何测圆的面积呢?方法有很多啊,这里 我用的是几何概型,建立一个直角坐标系,再画一个一乘一的正方形,里面有一个零点五乘零点五的小正方形,然后在这个一乘一的区域内产生随机点,那么随机点出现在小正方形里的概率就是四分之一,这不就刚好是小正方形和大正方形的面积之比吗? 如果这个时候我把小正方形换成一个半径为一的四分之一圆的话,这个关系也是成立的。 为什么要用四分之一元呢?因为后面产生的随机数是非负数啊,所以说我们要在第一项线解决战斗, 以圆点为圆心呢,也是为了方便计算。随机点出现在四分之一圆内的概率等于四分之一圆的面积,不以这个正方形的面积的啊,我们一下下啊,就可以得到了,圆的面积呢,是等于四乘以概率,再乘以大 正方形的面积。好,那么问题来了,这个概率怎么测?我们可以用频率去近视估计得到这个概率啊, 说人话呢,就是我们让随机点多次出现,然后呢,再统计这个四分之一园内的点的个数,再处以整个区域的点的总数,我们就可以得到随机点出现在园内的频率了。好,那么现在概率也得到了,正方形的面积也知道了,再乘以四呢,就可以得到了整个圆的面积, 再用圆的面积除以半径的平方啊,就可以得到派了,半径呢,是等于一的。接下来我们要把上面的数学原理写成代码,但是写代码之前呢,我们还是得先把算法给写一下, 算法的表达方式有很多啊,其实不必拘溺于某种形式的,你可以写一段伪代码啊,画一个流程图,甚至写一篇小作文。当然也不能太放飞自 我来写啊,因为你既要精准的表达数学内涵,又要易于理解。最后呢,还得是可实现的,因为我就见过有个靓仔啊,用了一个算法跑奔一台服务器了,我想在这个区域内产生 n 个随机点, 那么我就用 n 四循环啊,每一次循环就有一个随机点产生啊,然后我们再在这个零到一的区域内产生随机数, x y, x 作为横坐标, y 作为重坐标,如果有 x 的平方加 y, 平方小于一,我们就把四分之一元内的点的个数呢累加一。 这句话的意思呢,就是,假如有一个点坐标是 x y, 而 x 的平方加 y 的平方就是这个点到圆点的距离,然后呢再平方,如果这个点是在圆内,那么它的距离的平方呢,是小于半径的平方的啊,而半径呢是等于一的。好,我们到循环结束啊, 得到了圆内的点的个数为 k, 而整个区域内点的总数呢是 n, 我们用 k 除以 n 就可以得到随机点。在四分之一元内出现的概率,再乘以大正方形的面积一,就得到了四分之一个圆的面积,再乘以四,我们就可以得到了 以整个圆的面积除以半径的平方,也就是一,最终呢就得到了圆周率。 那么以上的文字呢,就是蒙特卡洛实验的算法,我们就是要根据这个算法去把它用代码实现出来啊,代码我已经写好了,我们来做一下代码的分析啊,这里呢我用的是抓把来实现的代码分成两大块啊,上面这块呢是数学原理的描述, 下面这块是主函数直行,这里表示的是循环。 xy 呢,是用的 random 函数去产生 一个零到一的范围之内的随机数。这里呢是做了一个判断, 如果说 x 平方加 y 平方小于一,那么四分之一元内的点的个数就累加一,这个是圆周率的计算公式。在这里我们可以输入我们实验所要用到的点的总数,我们先用一百个点来试一下, 算出来,结果呢是三点二啊,不是非常的准确啊,我们再运行一次,这次又变成了三点三二,证明这个一百个点呢个数还是太少了, 所以他的结果呢会波动比较大,我们再用一千万个点来重复一下这个实验啊,哎,我们发现了这个结果就非常准确了,三点一四一五,对吧?在这里感觉还是不够形象啊,我把程序又换了一下,做了个图形界面给大家看一下啊, 给你们留个作业啊,用蒙特卡落实验去求椭圆的周长怎么做。你们可以尝试像我这样用数学原理分析。然后呢再用算法把它写出来啊,我们下期详细讲,我们下期见。
905有趣的理工男 04:55查看AI文稿AI文稿
04:55查看AI文稿AI文稿知道三月十四号是什么日子吗?他是伟大的理论物理学家爱因斯坦诞辰的日子,也是伟大的物理学家史蒂芬霍金逝世的日子。今天我们除了要沉痛哀悼史蒂芬霍金以外,还要说一下三月十四号这个日子, 他也称之为派节。为什么叫派节呢?因为我们知道圆周率派约等于三点一四。今天我们讲一讲圆周率派是怎么推倒出来的。所谓圆周率呢,就是有一个圆,他呢有条直径叫地, 他的周长叫 c, 那么快呢,就等于周长与直径的比,这个比呢,不管圆的大还是小,那么他的笔质都是固定的啊。大家知道谁最早算出圆周率的吗?这个人呢,就是啊,给我一个支点,我可以翘起地球的人。阿基 阿基米德采用了一种方法,称之为割元法,割元法,用这种方法呢, 阿基米德计算出的圆周率的大小,他怎么算的呢?他说呢,这个圆的直径很好测,关键是他的周长不好算,怎么办呢?他可以啊,用一个圆的内接正六边形,用正 右边形的周长来近似于这个圆的周长。但是正六边形跟圆毕竟还是有差别的,所以怎么办呢?他又把正六边形再进行切割,变成了正十二边形, 用正十二边形的周长去近似圆的周长。他说正十二边形还是不行,那我们可以再切合,变成正二十四边形、正四十八边形和正 正九十六边形,那么他呢,就使用了正九十六边形,正九十六边形来进四圆。最后呢,他计算出来的结果,派约等于三点一四。 那么在五百年之后呢,中国有一位数学家,名字叫刘辉啊,在魏晋时期的数学家刘辉,那么刘辉呢,也采用了高阿基米德类似的方法,割圆法来计算圆的面积,只是他的方法可能更复杂一点,那么他呢,割出了三千零七十二根筋, 用三千零七十二平行的办法,他计算出的结果,这个结果呢,派约等于三点一四一六,那就更接近现在的值了。又过了两百年,中国有一个数学家叫祖冲之,祖冲之呢,他 采用了另外一种方法,称之为坠数的方法,这在正面坠啊,坠数的方法算出的派呢,约等于三点一四一五九二六 这个数字,这也是我们小学学习的时候常念的一个数字。但是坠数到底是什么方法,大家不是很清楚啊,这个方法已经失传了,于是很多数学家在推测祖冲之到底采用了什么方法,那么直到一千多年之后呢,西方才重新计算出来了,到我们这个精度啊,所以在这一点上,我们领先了西方一千多年。 那么有同学说,我现在大概明白了,你告诉我具体阿基米德是怎么算的,能不能我也用手算一算呢?你也是可以的。其实呢,这个方法并不是很难,我们来看啊,一个圆,我们假设他的半径是一圆形,是 o, 这个是 a, 我们把它分成正右边形的 一个边长叫 ab 啊,因为啊,我们把它分成正 n 边形, 在正 n 边形的时候呢,他的边长叫 l n, 那么我们再问正二 n 边形, 他的边长叫 l 二 n 又应该有多大呢?其实这个并不难算,大家看,我们在这里啊,做一个脚跟线,中间有个焦点叫 m, 交出这个点呢,叫 n, 这个边长不就是 l 二 n 吗? 对不对? l, 我们通过这个几何关系简单推导一下,就可以得出这样一个结论, l 二 n 呢,他应该等于根号下二减去根号下四减去 l n 的平方。可以有这么一个结论,有了这个结论之后呢,我们可以说啊,当 n 等于六的时候,就是六边形啊,正六 变形,这个 l 六呢,其实是一啊,那么 l 十二是多少呢?我们带入这个公式去算,等于根号下二减去根号下四减一的平方,那这个数呢,就是根号下二减根号三啊。 十二变形算完了,继而可以算二十四变形,算出四十八变形,算出九十六变形。假如我们算到这为止,那么我们就可以进四出这个圆周率了啊,这个圆周率派等于什么呢?等于周长除以直径, 周长是九十六边形,再乘以每个边的边长,再除以直径。我们刚才设半径是一,直径就是二,对吧?把这个数据带入最后这个数据呢,就是三点一四,也就是阿基米德的结果。
1.1万李永乐老师 01:12
01:12 00:17
00:17
猜你喜欢
- 1151🍊橙子老师







