圆形是立体图形吗
粉丝26.5万获赞92.4万
相关视频
 06:29查看AI文稿AI文稿
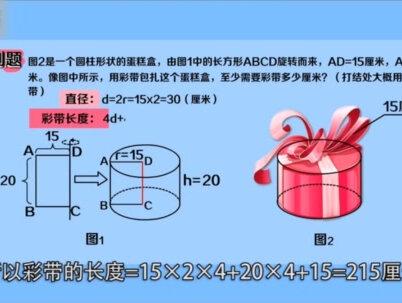
06:29查看AI文稿AI文稿这节课的内容是旋转柱体圆柱。我们知道圆可以看成一条线段,绕着他的一个端点旋转,形成了一个封闭图形。 类比这个过程,我们把长方形绕着它的任意一边旋转一周,就会得到一个立体图形,这个图形我们称为圆柱。 生活中像接力棒、水管、粉笔等都是圆柱。如图可以看出,圆柱有以下特征, 一、圆柱的上下两个圆称为圆柱的底面,它们半径 r 相等,等于 长方形 a、 d 边的长度。二、两个顶面间的距离叫做圆柱的高,记为 h, 等于对称轴 c、 d 的长度。 三、圆柱有无数条高且高的长度都相等。 根据以上特征,如果我们把上竖的长方形的 a、 d 边作为对称轴旋转,就会得到一个新的圆柱,这个圆柱底面圆的半径就是 c、 d 的长, 这个圆柱的高就是 a、 d 的长。这是两个不一样的圆柱。 我们来看一个例题。图二是一个圆柱形状的蛋糕盒,是由图一中的长方形 a、 b、 c、 d 旋转而来, a、 d 等于十五厘米, a、 b 等于二十厘米。 像图中所示,用彩带包扎这个蛋糕盒至少需要彩带多少厘米,打结处大概用十五厘米彩带。 观察彩带,发现如果要用彩带把圆柱体缠绕,会产生四个顶面圆的直径和四个的高,所以关键就是要求顶面圆的直径和高。 顶面圆由 a、 b、 b、 c 旋转而来,直径为十五乘以二,等于三十厘米 高,由 cd 旋转得到,就是 a、 b 二十厘米。所以彩带的长度等于十五乘以二,乘以四加二十乘以四加十五,等于二百一十五厘米。 本题只要清楚旋转前长方形两边长分别是旋转形成的圆柱的曲面半径和高,就能轻松搞定。 下面我们研究一下圆柱的展开图。当圆柱体沿着高展开后,包括两个圆和一个长方形, 如果不沿着高线,还能展开成平行四边形。 注意,这个长方形可不是前面旋转的那个。这个长方形它在展开前是圆柱的曲面,也叫侧面,所以它的长就是圆的。周长 c 等于二派 r, 宽就是圆柱的高 h。 如果周长和高相等时,侧面就是正方形,它的面积也很好求 周长乘以高 c、 h 等于二派 r h。 圆柱侧面积的实际应用主要有两种题型,一种是圆 圆柱形物体的用量面积问题,比如烟囱、塑料、水管等没有上下底的圆柱形,计算其物料面积只需要求侧面积即可。另一种是压路机问题,压路机的前轮是圆柱形滚筒, 压路面积就是旋转圈数乘以侧面积。比如这道题,压路机的前轮是圆柱形,里面半径一点五米,侧面展开是正方形。前轮每分钟转动十周, 每分钟前进多少米?一小时压路多少平方米?前轮每分钟转十周,就能前进十个 正常的路,即十乘以二拍 r 等于十乘以二乘以三点一,四乘以一点五等于九十四点二米。 我们再来算压路面积,每转一圈压过一个侧面面积。由于侧面展开是正方形,所以轮宽等于里面,周长等于二派 r 等于三派米, 故前轮的侧面积等于三乘以三点一,四乘以三乘以三点一、四等于八十八点七三六四平方米, 一分钟前进十周,那么一个小时就能前进六十乘以十周等于六百周,所以一小时压路六百乘以八 十八点七三六四等于五万三千二百四十一点八四平方米。 这节课我们就讲到这里总结一下。首先我们讲了圆柱的形成以及两圆一侧面。 第二我们讲了圆柱侧面展开的长方形的长宽与圆柱底面半径高的关系, 以及实际应用的两大类型。
198小初高教辅收藏夹 00:46
00:46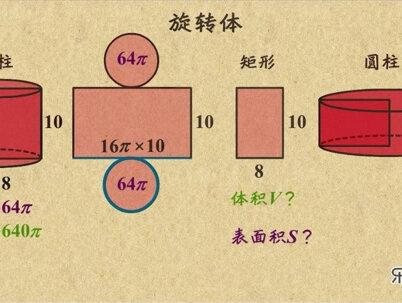 03:06查看AI文稿AI文稿
03:06查看AI文稿AI文稿展开图是把立体图形变成平面图形的方式,而给你个平面图形,想让你把它变成立体的怎么办?只要让他动起来就可以了, 可以沿着一个方向运动,也可以沿着一条边旋转。这个视频就来聊聊旋转的事。这是一个长方形,也叫矩形,他绕着这条边旋转一周,哎,是个圆柱, 当然长方形两边未必一样长,所以这么转出来的圆柱跟刚才的不一样。那么问题来了,如果我告诉你这个长方形长十宽八,那沿着两条边分别转出来的圆柱体,他们的体积和表面积你会求吗? 先看这个圆柱,高是十,底面圆的半径是八,他的体积是底面积成高,底面积是派 r 方,也就是六十四派,高是十,那体积就是他俩乘起来得六百四十派。 这里要说明一下,中学阶段的派就不再估算为三点一四了,计算结果带着派就行,体积搞定了。再来看表面积, 你知道圆柱展开是两个圆和一个长方形,这俩圆一样,面积都是刚才算的六十四派,而这个长方形,他的宽是十,长是圆的,周长也就是二派, r 算一下是十六派,这样长方形的面积就是一百六十派了, 三个面积加一起就是一百六十派,再加两个六十四派,结果得二百八十八派,这就是援助的表面积。 第一个圆柱 o 了,那第二个圆柱的体积和表面积你会算?不对了,对于这个圆柱来说,高是八,底面圆半径是十,体积还是底面积成高,底面积是派 r 方,也就是一百派,高是八,体积就是把他俩撑起来得八百派体积 欧了来算表面积,他展开还是两个圆和一个长方形,这俩圆面积都是一百派,而这个长方形宽是八,长是这个圆的周长,也就是二派 r 得二十派,这样长方形面积就是一百六十派了。 三面积加一起就是一百六十派,再加两个一百派,结果得三百六十派,这就是这个援助的表面积。怎么样?长方形旋转的问题是不是非常简单?那么问题又来了,这个直角三角形沿着直角边旋转一圈是什么图形呢? 两条直角边不一样,这就得分情况了,绕着这条直角边这么转一圈,或者绕着这条直角边这么转一圈,都是圆锥。如果我把这个直角三角形砍一块成了直角梯形,你能告诉我这个图形沿着这条高转动会形 成啥不?那就让他转一圈转成这样。这东西是啥?这个叫圆台,其实就是圆锥,再减去一个圆锥,想想你这直角梯形咋来的?再一转就是这个圆台了。 转的差不多该总结了,平面图形旋转可以形成立体图形,绕不同边转出来的图形可能不一样,长方形绕边旋转是圆柱,直角三角形绕直角,边旋转是圆锥。 直教梯形绕着高旋转是圆台。好了,为师这就讲完了,徒儿们速速刷题去吧!
1104乐乐课堂天天练-初中数学 14:22查看AI文稿AI文稿
14:22查看AI文稿AI文稿这个视频我们来讲一下立体图形的直观图,我们上个视频呢,讲的是平面图形的直观图,它立体图形的直观图和平面图形的直观图,它们的区别在于就是 立体图形的主观图呢,多画一个 z 轴啊,多画一个 z 轴。那我们可以先把这个平面图形这个坐标系啊,坐标系,这是 x 轴,这是外轴啊,乘四十五度角,或者是乘 一百三十五度角,这是 x 轴,这是 y 轴。那 z 轴呢?我们做垂直于这个呢,我们就做垂于垂直于 x 轴的一条线 z 轴。那么这个呢?我们做垂直于 y 轴的这条线啊, z 轴。嗯,主要是这两种 画法啊,这两种画法,那平行于平行于 z 轴的线段, 它具有哪些特性呢?就是平行性保持不变,还有就是它长度和长度都会保持不变啊,长度不变 啊,长度不变,平行性和长度都不变。那我们就像这种呢, x 轴呢,它的平行性和长度不变的。 y 轴呢?平行性不变,但是 他的长度要减半啊,这是我们平面图形的时候哎,外轴呢,平行要减半,但这种呢,平行性和长度都不变啊,这是我们看后面的练习啊。第一个是用斜侧画法画一个冷长为 三厘米的正方体啊,听正方体,那我们画它第一步呢,先画轴, 画轴,画轴,我们就画一个,这是 x 轴啊,这是 x 轴,然后 y 轴,然后 z 轴啊 z 轴,那我们就把轴画出来了,画出来以后画底面。第二步画底面,画底面, 底面它本来是一个正方形啊,底面是个正方形,我要画成它的直观图呢,那就是这是冷长为三的正方形,那,那我可以取这个是 a、 a、 d, a、 b 等于三啊, a、 b 是等于三的啊,等于三。在这个 x、 e、 x 轴的这个长度是保持平行性,保持不变的,那 y 轴上呢?那我们就要 减半啊,外轴是减半,原来是三,现在要变成二分之三啊,二分之三, 那就是 a、 d 等于二分之三,然后沿着 d、 d 点呢?我做平行圆轴的一条线啊,一条线,然后,呃,一直到 c 点,那么 d、 c 呢?和就等于三啊,和这个 a、 b 的长度是一样的,等于三 啊,比如说到到这等于三,哎,我们确定 c 点的坐标, c 点坐标,那我再把这个 b、 c 把它连接起来,那这个就是下面这个正方形的直观图啊,底面我画出来了,第三画侧棱,画侧棱, 侧棱怎么画呢?一个是 a, a 撇, a, a 撇我,那我们就是 a 这个 z 轴,我们画这,这个过低一点呢,我做 做过 d 点,我做平行于 z 轴的一条线,过 c 点,还有过 b 点啊,都分别做平行于 z 轴的线, 然后在这个 z 轴上,我取 a、 a 撇,那么它正好等于三, a 撇等于三。比如在这 a、 a 撇等于三,那么在在这个 这条线上啊,我取 d、 d 撇等于 三啊,等于三。 deed 撇等于三,然后在这个这个这个线上啊, c 这个线上,那我们取 c、 c 撇等于三,然后在这里面我们取 b、 b 撇等于三。然后我按照顺序把这些 a 撇、 b 撇、 a 撇、 b 撇,然后 b 撇、 c 撇, 还有 c 撇、 d 撇,我们把它连接起来,连接起来,那这个正方形就画出来了啊,这个是 正方形, a、 b、 c, d, a 撇, b 撇, c 撇、 d 撇啊。第四步, 成图啊,成图以后我们把一些辅助线啊,把这一辅助线擦掉就可以了,那我们这是我们的直观图就出来了,这是第一个,我们看第二个,用斜二侧画法画一个正六棱柱的直观图, 一个正流六棱柱,那两个底面呢?都是正六边形啊,两个正六边形。我们画一个正六边形,正六边形, 这是一个正六边形,两个底面是正六边形。那么最主要的先把两个底把底面画出来啊,底面画出来,那么正六边形。我如果要是取坐标轴的话,我用对称性,这样可以这样取, 这样去坐标轴,那我画成直观图了,那如果这个边长是二的话,那我们就可以看边长是二,那 这个我把它连接起来的话,这个这个角度,这整体是一百二,那这个是六十度,那这个等边在线,所以这个是二,这个也是二啊,这是二,那所以那这个这个长度呢?我可以, 我可以画它的直观图。直观图怎么画呢?就是 x 轴和 y 轴呢,是乘四十五度角,乘四十五度角,这样, 然后我们取取这个 e, 这是 o、 d, o 为原 以终点啊,这是中,这是 x 轴, y 轴以 o 为终点。然后啊,我在 x 轴上,我取一个 a 啊,取,比如说我取是 a、 d 吧,我取 a d, a d, 那么它是等于 整个等于四的,它关系不变啊,都是四,这是四,那么就取 a、 d 等于四,这是 a, 这是 d 啊, a d 等于四, a d 等于四,哎,这个是 a、 d, 这个两个点就确定下来了,这两个点就确定下来了,那我要确定这其他点呢?那我我首先我要确定这个点, 这个点,这个长度,我们在外轴上的这个点确定下来,这个点,这个长度怎么算呢?这个是六十度,这是二,那么二乘以三六十度,那就是根号三,也就是根,这个长度是根号三,那我但是在 直观图上要减半,就是二分之多少三,那我就可以取这个零,这个 o 啊, o g, 假如 o g, 而且确定 g 的 g 的这个位置啊, og 呢?是等于二分之高三的二分之高三啊,这个这个长就是这个长度的一半啊,这个长度的一半,那 把这个点确定下来了,然后我再确定这里这个这个这个长度仍然是二啊,这个长度仍然是二,那我们就沿着过这个 g 点,我做一个平行线啊,平行线,然后以 g 为中心,然后我们来确定,确定一个 确定和这个这两个值。一个是啊, e f 啊,这边是 e, 这边是 e, 这边是 f, 这边是 f 啊,这两个,这两个点,这两个点确定下来,也就是 e f 的长度是一啊,那中间 g 呢?是的终点,那这个我们把 这两个确定下来了,那同样的这个呢?这个对称性这个点呢?这个点我要再确定这个点,那么 o h 呢?也是等于二分之根号二啊,去减半,那那这个是 h 点,然后沿着 过 h 点呢?我做平行 x 轴的一个线,那么 b c 以 h 点为终点,那么 b c 呢?长度是等于 b c 的长度是等于二的啊, b c 的长度是等于二,哎,我们可以确定确定一下,它的 这是 o 啊,这确定一下这个是 b 和 c 的点,那至此我们这总共正六边形的六个点,我们就确定下来,然后我们就可以把它连接起来啊,顺序的连接起来。 哎,这个就是我们这个就是正六边形的一个直观图啊,正六边形的一个直观图, 正六边形的,呃,底面的直观图,那我们现在在画侧棱啊,侧棱,我先把这个 z 轴画出来, z 轴是这样垂直于 x 轴的,这是 z 轴、 z 轴。然后我们通过这六个点啊,这六个点我们分别去画平行于 z 轴的线,比如说这个线, 这过 f 点,过 e 点,过 d 点,过 d 点,然后过这个 c 点,过 c 点,过,这是 b 点,我就做平行于它的 线啊,平行线,那然后我们是正六棱柱,那个侧棱呢?并没有什么要求啊,你比如说我设成三也可以啊,你设成三, 然后我们取这个 a a 撇啊,在这个线上我取 a a 撇,那么等于三,然后在 b 呢,这个线上呢?我取 b, b 撇,等于三,然后在 c 这个线上呢,我们取 c c 撇,等于三啊, c, c 撇等于三。还有这个这是 d d 撇, d, d 撇, d, d 撇等于三啊, d, d, d, d 撇,那这个 e 呢?往上一点,那么 e, e 撇等于 e, e 撇等于三。那 还有就是这个 f f 点, f 点往这边走啊,那么这个它也是把这个点 f f 撇等于三,那我们就把剩下的就把这个顺序呢给它连接起来,这个是 a a 撇,然后 b c 撇,然后是 d, 这是 d c c 撇, d 撇连接起来,然后 d 撇, e 撇连接起来, d 撇, e 撇连接起来,然后这个是 e 撇, e 撇、 f 撇,还有 a 撇和 f 撇,哎,我们就把这顺序 连接起来,就整个这个正六棱柱就画出来了啊,把剩余把一些辅助线把它擦掉就可以了,这是正六棱柱的直观图。 我们看第三,那一个简单的组合体,上下分成两部分,下部呢是一个圆柱,上部呢是一个半球,并且半球的球心就是圆柱的上底面圆心,画出这个组合体, 那么先画一个圆柱啊,下部是个圆柱,我们先画一个圆柱。圆柱怎么画呢?就是先啊,比如说这是 x 轴啊, x 轴, 这是 o, 这是 x 轴 x 轴,那么圆柱呢?是,呃,我把那下底面画出来,他的下底面是个圆柱,那么下面呢是个椭圆的模型,我们画一个 椭圆就可以,然后上底面圆柱的上底面平行于 x 轴的一条线, 平行于 x 轴,那么就是 x 撇轴,那么这个点,那这个这个线呢?就是和和这个垂直啊,和 o o, 这是 o 撇, o o 撇和 x 轴垂直,那垂直,那么这个是, 那这个是它它这个轴的圆心啊, x 撇,这个轴的这个这个圆心啊,这个这个是圆点啊,圆点,然后依这个圆点呢,我们也是画一个, 画一个和他同样的一个椭圆,同样的一个椭圆, 也就是这个长度,比如这是 a b 吧,那么这个是 a 撇 b 撇 b 撇 a 撇 b 撇,它们的长度是一样的,然后画一个椭圆,画一个椭圆, 然后我们把这个 aaa 撇连接起来,把 bb 撇连接起来,把 bb 撇连接起来,那么这个就是一个圆柱,这圆柱我们就画出来了,那么下面下面是个圆柱,上面呢是上部是一个半球,并且半球的球星和圆柱 上圆柱的上底面的圆心啊,圆心在这圆心是一样的,那我就画球的话,我就画一个半圆就可以了啊?画一个半圆, 哎,画一个半圆就是一个圆球球体,这半球体,那么这个指关图我们就可以 画出来了。啊,这个是,这是 z 轴啊,这整体是个 z 轴啊。那么这个是怎么画这个组合体的直观图?
94洪邦数学 05:04查看AI文稿AI文稿
05:04查看AI文稿AI文稿当时社会,人们以天为被,以地为床,过得那叫一个惨。后来学会了盖房子,地板四面墙,再搭个屋顶, 防雨防风防狗熊。这个棱角分明的房子就是我们熟悉的长方体。他有六个面,前后左右上下。为啥这么分呢?因为相对的面一样大,要不房子就得塌。房子的犄角旮旯是长方体的顶,顶 数一数有八个。拿这个来说,他连出来了三条线,这些线分别是长方体的长、宽和高。这个方向的都是长,有四条,同样宽和高也各自是四条,加起来十二条线。大明棱要 房子盖的再方正一点,就成了正方体,也是六个面,八个顶点,十二条狼。但是正方体可不只是对面相等了, 他的所有面都一样大,并且十二条棱也一样长。你上看下看,左看右看,正方体都一个模样。图形出来了,我们得知道两件事,第 一,他的脸皮有多大,第二,他的脑子有多大。脸皮学名表面积。把这俩扔到染缸里,所有被染上色的地方就是他们的表面积。长方体的六个面分三组大小分别是长城宽、 长乘高和宽乘高。总脸皮大小二倍的长乘宽、加长乘高、加宽乘高。 正方体脸型比较单一,总脸皮是六倍的 a 的平方。再来看看脑子,脑子行不行全看三条棱。长方体的脑容量由长宽高决定,他的脑容量就等于长成宽成高,这就是长方体的体积。而 正方体就属于头脑比较简单的那种,直接是冷场,成冷场成冷场,也就是冷场的三次方。最后隆重介绍一位古希腊的大爷阿基米德同志, 他干的最有名的一件事就是洗澡,哈哈哈,别人洗澡唱歌,他洗澡解题,并且还是把国王的王冠往澡盆里丢的这种说法,就因为他的这个癖好。水中浸雾问题,也叫阿基米德问题。来 这个水箱,把长方体铁块扔进去,无非三种情况,还漏着全淹了,水洒了,这学问大着呢,要不你去浴缸想想?时间始终向前,永不倒流。但时钟上的指针却不一样, 他绕完一圈就又回到起点,只看这个指针,他绕一个端点转一圈,划过的就是圆的面积。摊煎饼果子也是一样的道理,小木棍一刮,一个圆就出现了。 如果这根小木棍在厚点,那他扫过的可不仅仅只是一个圆了。从侧面看会发现木棍有了高度。现在扫完一圈,得到的是一个圆饼。圆饼这名字确实很形象,但是在数学中他叫 圆柱,顾名思义,圆圆的柱子嘛,圆柱是怎么来的呢?刚刚的木棍从侧面看就是一个长方形,这个长方形绕着他自己的一条边旋转一周,得到的就是圆柱。 绕短边可以绕长边当然也是没问题的。这个圆柱就比刚才的那个更瘦更高。华表的柱子,大师兄的金箍棒,还有这种蛋糕,都是圆柱。 圆柱上下的两个表面都是圆,并且大小一样,统称里面,与之对应,圆柱外面这一圈叫做侧面。 大家觉得这个圆柱更应该叫圆饼,可能是觉得他不够高,这个高其实就是圆柱两个底面之间的距离, 不管高有多长,他们都是圆柱。说完了圆柱下面再来看看圆锥,一看到追这个字,就感觉好像被扎了一样,因为追就是尖尖的东西。 圆锥也一样,一头是尖的,至于另一头当然得是圆的了。生日帽、喇叭、漏斗都是圆锥的形状,但这些就都不是圆锥, 只知道样子还不够。圆锥到底是怎么来的呢?刚刚说过,圆柱是一个长方形绕一条边转一圈所得到的图形。圆锥呢,是一个直角三角形绕 其中一条直角边转一圈所得到的图形。下面的圆照样叫底面,上面的尖叫顶点,顶点到底面之间的距离就是圆锥的方。
191宋家两公子 04:02查看AI文稿AI文稿
04:02查看AI文稿AI文稿这节课我们一起来学习简单组合题。首先来复习之前所学习的简单结合题,我们把能柱、能锥、能台、圆柱、圆锥、圆台以及球呢称作简单结合体,而且这些是常见的简单结合体。 另外呢,能住、能追、能抬,他们三个呢是由平面、多边形组成的,所以我们把他们三个叫做多面体、 圆柱、圆锥、圆台。球呢,他们是有一条固定的旋转轴,有一条曲线或者是一条直线,然后这条固定旋转轴旋转以后呢,形成一个曲面,我们把这个曲面封闭起来,那么得到一个旋转体,所以他们四个是旋转体。 接下来我们要学习三个新的知识,是柱体、锥体以及台体。什么叫做柱体呢?我们把兰柱和圆柱 都有柱这个字叫做柱体,他们俩叫做柱体。而人锥与圆锥呢,他们俩都有锥这个字,所以叫做锥体。 那么把他们俩呢叫做台体,轮台和圆台叫做台体,所以得到铸体、锥体、台体以及球。接下来我们学习这节课的新教程,简单组合体 有简单几何题,简单几何题就是刚才我们所讲的常见的那些圆柱、圆锥、圆台、轮柱、轮锥、轮台。求这些组合而成的几何体呢?我们称作简单组合体。 简单组合体分为两种,第一种呢是由简单几何体拼接而成,比如说第一个由简单几何体拼接而成,有一个长方体和一个四能锥拼接而成。另外一种呢,是由简单几何 撇截去或挖去一部分而成。比如说后面这两个,他们是挖去了一部分,这里呢是一个圆台,挖去了一个圆锥,而这里呢是一个球,挖去了一个六面体得到。接下来我们做一下练习题,来巩固一下。 请描述下列组合体的结构特征,下面呢有三个图,他们的结构特征是什么样子呢? 个个组合体分解为简单几何体,我们将各个组合体他们都是组合体,那么分解为简单几何体,刚才有讲简单几何体呢,有柱体、锥体、抬体以及球。 那么先来看第一个,第一个的话,它上边呢是一个圆锥,而下边呢是一个圆台,他们俩是拼接而 成的,所以是由一个圆锥和一个圆台拼接而成的组合体。第二个呢,第二个他是一个长方体,长方体呢,他截去一个角,一个角,其实这个角就是一个三人锥, 将它是一个三轮锥,所以我们可以把它描绘成是用一个长方体截去了一个三轮锥后剩下的部分组成组合而成。它是截去了一部分,这个是拼接,这个是截去,那么这个是挖去了一部分, 这里呢有一个圆柱,里边呢挖去了一个三棱锥,所以是由一个圆柱挖去了一个三棱锥,剩下的部分得到了组合题。那么这就是这个题。最后我们来做一下小节,这节课呢,我们复习了能柱、能锥、能抬圆柱、 圆这个圆台,以及求我们之前所学习的简单几何题。那么他们几个呢?他们上面三个我们称为 多面体,他们下面四个呢,我们称为旋转体。现在呢,我们又把他们两个呢叫做柱体,他们俩呢叫做锥体,他们俩叫做抬体,他呢是丘。那么这节课呢,我们学习了新的内容,有 关简单组合题,有简单几何体组合而成的几何体呢?我们称作简单组合体,一种是由简单几何体拼接而成,这个是拼接而成。另外一种呢,是由简单几何体挖去或截去一部分而成。这两个呢是挖去了一部分而成。好,这节课我们就讲到这。
187滴答课堂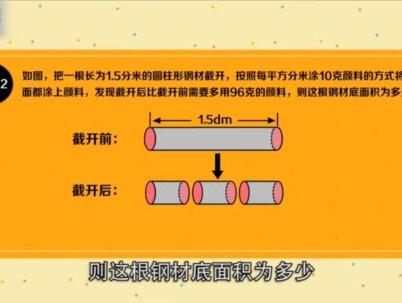 08:36查看AI文稿AI文稿
08:36查看AI文稿AI文稿这节课的内容是多角度切割圆柱的切割。上次课我们研究了圆柱的侧面展开,今天我们将对圆柱进行多角度切割。我们先来按照劈木头的方式处理圆柱。 这种切法叫竖切,即用一个过圆柱对称轴的平面去切割圆柱,圆柱被切割成一模一样的两部分, 这样切割形成的两个切面, a、 b、 c、 d、 e、 f、 g、 h。 我们称为圆柱的轴截面。这两个轴截面完全重合, 都是长方形。特别的是,当圆柱的底面圆直径 d 等于高 h 时,轴节面是一个正方形边, a、 b、 c、 d、 f、 g、 e、 h 是底面圆的直径, 另一边 a、 d、 b、 c、 e、 f、 g、 h 是圆柱的高。因此,圆柱轴截面的面积 s 轴等于 d, h 等于 r r、 h。 这个公式超简单,其实就是长方形面积公式。对比上节课的原著册,面积公式 s 册等于二派 r、 h, 我们就能发现轴截面面积和圆柱侧面积的关系,即 s 侧等于派倍的 s 轴,圆柱侧面积是轴截面面积的派倍。 当用一个平行于轴接面的平面去切割圆柱,将圆柱分成不等的两块,但两个切面还是长方形。一边 a、 d 还是等于圆柱的高, 另一边 a、 b 小于圆的直径,所以这些切面面积都小于轴接面的面积。 即用所有的平行于轴接面的平面切割圆柱时,得到的切面中,轴接面的面积最大。 我们来看一个例题,已知圆柱底面半径为一分米,轴截面是正方形,则圆柱的侧面积是多少? 根据提议,轴截面是正方形,所以圆柱的高等于底面直径二乘以一等于二分米, 那么轴结面面积 s 轴等于二乘以二等于四平 方分米。根据 s 侧等于派背的 s 轴得到 s 侧等于四派平方分米可见。记住这个公式后,可以直接由轴结面面积推出侧面积。 下面我们再来按照切香肠的方式处理圆柱。用平行于底面的平面去切割圆柱,称为横切。会发现将圆柱分成两个小圆柱, 切面是与圆圆柱底面一模一样的圆。经过这样的一次切割,比原来多了两个底面,如果切两次 呢,则多四个面,切三次多六个面,以此类推,切 n 次就多二 n 个切面。 这里超级学员要注意,如果改一下说法,横切切成两段,那么还是多四个面吗?显然不是, 切成两段,只是切了一次,所以只是多了两个面,以此类推。切成 n 段,只是切了 n 减一次, 所以多了二倍的 n 减一个面。 我们来看一个例题,如图,把一根长为一点五分米的圆柱形钢材解开,按照每平方分米铺十克颜料的方式,将所有底面都涂上颜料, 发现解开后比解开前需要多用九十六克的颜料,则这根钢材底面积为多少?将圆柱解开后,比原来多了四个底面, 所以需要多用的颜料就涂在多出来的四个面上了。 多用了九十六克,则每个底面用了九十六除以四等于二十四克颜料, 所以底面积等于二十四除以十等于二点四平方分米。 最后我们再来斜切圆柱,即用不平行于底面的平面去结圆柱。 斜切得到的切面很奇怪,不是我们见过的平面图形,甚至到初中也不会见到,只有到高中才能见到,叫做椭圆。 很明显,出题老师不会让我们求斜切后切面的面积了,但是会让我们求切开后的侧面积。如图,将一个底面周长为十二点五六 厘米的圆柱斜着截成两个形状完全相同的立体图形,此时每个立体图形侧面积为多少?注意,这道题没让你求截面椭圆的面积,而是求侧面积。 由于结后两图形形状完全相同,所以他们的侧面积是圆柱侧面积的一半。 圆柱的基底周长还是十二点五六厘米,高为三加五等于八厘米, 所以圆柱侧面积 s 侧等于 c, h 等于十二点五六乘以八等于一百点四八平方厘米。所以所求的这个不规则图形 的侧面积是一百点四八除以二等于五十点二四平方厘米。 这节课就讲到这里,我们来总结一下。首先我们讲了圆柱的三种切法,竖切、横切和斜切以及得到的切面。 然后我们讲了竖切、中轴结面面积与侧面积的关系, 横切中切的次数与增加的底面数之间的关系, 斜切后侧面积的求法。 最后我们讲了利用斜切来解决不规则圆柱的侧面积问题。
239小初高教辅收藏夹 04:00
04:00 00:40查看AI文稿AI文稿
00:40查看AI文稿AI文稿真实立体几何图形,丰富的形状便于低年级认知。创意造型搭建,开发孩子想象力,边搭边学,寓教娱乐,趣味学习。圆形六龙体、正方体、菱形、 三角形、梯形,四分之一长方体、椭圆柱,平行四边形四龙锥,二分之一长方体,三角形,长方体、 圆棱锥,圆形圆柱。帮助孩子认知形状,看颜色。几何形状是孩子小学全年级的课程。
210小瘦老师爱分享。








