刘鸿文材料力学弯矩图画法

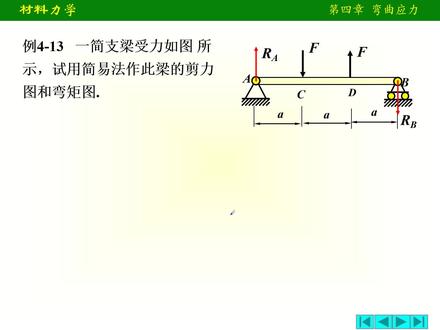
大家好，今天咱们呢再给大家讲呃，梁的简历图和玩具图的画法啊，这是一个简直梁上面呢做了两个合载， 嗯，这个盒仔是送在这个对称的位置，但是我们的盒仔呢，是一个是指向下，一个指向上 啊。呃，由于呢，我们的这个核展是千锤方向的，然后 a 端呢，虽然是固定角质做，那么 a 端的水平力实际上是为零的啊， 因此呢，我们根据这个核载图呢，它应该是一个反对称核载啊，就是核载图应该属于反对称核载。呃，那么这个反对称核载，我们这二 a 和二 b 怎么来计算呢？呃，根据对称原理，那么 ra 和 rb 一定是这个成为一个反对称的力啊。呃，但是这里我们要注意啊，呃，可不能直接就说 ra 啊，等于 f， 然后 rb 呢，也等于 f， 然后一个向上，一个向下，如果这样直接判断他的 制作反应的话，那这个就错了啊，因为什么呢？像这种情况，你是只考虑到外方向的这个平衡，但实际上呢，我没有考虑他的这个例句的平衡 啊。所以说这个题我们应该怎么分析他的这个制作法例呢？我们可以用利偶的等效性啊，我们这个核载呢，它形成了一个利偶，是 f 乘上 a 啊，是一个逆时转的，因此呢，根据利偶的平衡，那么 r a 和 r b 呢，一定也形成一个反利偶和我们这个利偶平衡，所以说他应该等于谁呢？ r a， 当然或者是 r b 啊，呈上 这个 a 点到 b 点之间的距离三倍的 a， 也就是说呢，二 a 和二 b 的大小应该相等，方向应该相反，这符合反对称原理。另外他们两个形成的一个立偶呢，要与合在 f 所形成的理由啊，这两个 f 所形成的理由应该平衡，因此这样呢，我们得出这个 r a 啊，等于多少呢？三分之 f， 然后 r b 呢，也是 三分之 f， 然后他们两个的方向就是我们途中所表示的方向，一个向上，一个向下 啊，那么这样呢，既满足了外方向的平衡啊，然后呢， 他也符合我们的这个立具的平衡条件啊，所以应该这样来计算我们的制作返利啊，所以这个这个是我们需要要注意的。好，那么制作返利知道了以后呢？嗯，下面我们就开始画这个 简历图和弯印图了，那么这个简简历图怎么画呢？像这个简历图很简单，根据对称原理，简历图一定是一个反，这个一定是一个正对称。这个在上一个视频当中，我们给大家讲过原理啊，那么他的弯距图一定是一个反 对称。好，那么我们画这个简图是这样的啊，画一条轴线，从左向右画看，从这个轴线看上面的合载图哈， a 端有个向上的力，三分之一，好，那么我们就向上图变三分之一 f， 然后 ac 段呢，没合在 水平线，对吧？根据问分原理，那么到了 c 点以后呢，他有一个向下的集中力， 那么像应该向下图片，图片多少呢？就应该是三 f 图片 f， 那么上边是三分之一是吧，总的图片只是 f， 所以说应该下来多少呢？三分之二 啊，所以这个呢是三分之一，下面的是三分之二啊，实际上呢，上面这个就是 c 洁面左侧 侧的简历，下面呢是 c 洁面右侧的简历。好，那么从 c 洁面右侧，然后向右 画眉和在从 c 到地的这个左侧眉和在画水平线啊，画水平线好画到地洁面的左侧啊，所以说这个值呢，就应该是三分之二的 f 啊， 画到地洁面的左侧，那么地洁面呢，有一个向上的集中力啊，那我们就要向上涂变像，涂变多少呢？涂变 f 下边是三分之二， 那么再上去三分之一啊，正好和这个上面这个 ac 段的图形是平齐的啊，好，那么这个三分之一就是地截面右侧的减 好，从地洁面再往右画水平，先过来，好，到了臂洁面就是臂直坐，掌有一个向下的三分之一的力，好，正好回到轴线上去，那这个简历图就画完了。 把正负号表示出来啊，正负号表示出来，然后呢把数据 表示出来。好，这个完整的简历图就画完了啊，所以这个图呢，就是这样来的啊，这个图就这样来的。好，所以简历图呢，很好画啊，是一个正对称的，对吧？这个简历图形 总是有核载图，这个对称性是反着的。然后我们画弯距图啊，画弯距图的话呢，实际上我们就就是确定 a 点 c 点 d 点 b 点的弯距 行了啊，那么同样呢， a 支座他是在杆的端部啊，是个角支座，没有外力偶，弯距应该是为零 啊，那么同样 b 直做最右边，他也是为零啊。呃，然后 c 点呢，我们看啊， c 点的弯距，你也可以根据这个简历图，就是这个 ac 段简历图的面积，是吧， 或者说呢，直接用 ra 对 c 点取句，所以说 c 点的弯距应该是 三分之一的 f 乘上 a， 哪受拉呢？你可以看和载图，是吧？他对 c 点的距呢，是顺神转的是吧？而且呢，这个力呢，他是在 c 的左侧是吧？ 那么我们不是玩具是左顺右逆为证吗？所以说他应该是个正玩具，下侧手拉的，或者你就看我们的简历图的面积，是正面积，那产生的是正玩具，所以他也是下侧手拉的。实际上你求到这以后呢，地点就不用求了，地点一定和他反对称 啊，根据对称原理，地点一定是和他反对正好， a 点是为零， b 点为零， c 点是下侧受拉的 三分之一的 f 乘上 a 啊，那么地点呢，和他反对称，那就应该是上面手拉的三分之一 f 了，对吧？好，然后呢， 这个 db 段连一条直线，连的直线，那么这个时候呢， cd 段我们也是中间没合，在连直线就可 可以了啊，连直线就可以了，是一个反对称的，对吧？好，所以这个是三分之一 fa， 好，上面呢，这一点也是三分之一的 fa 啊，就这样一个反对称的图形，那么要注意哈，就是 ac 段的这个斜直线和 db 段的斜直线应该是平行的，因为上面的简历图， ac 段的简历图和 db 段的简历图 完全是一样的，是吧？简历的正符号大小都是一样的，所以这两条斜着线应该是平行的，因为简历是吧，和弯距的关系就是弯距在这个某一个地方的斜率就等于它的相应的这个简历直嘛，是吧，这样往里涂就画出来了，是吧？所以你看，我们符合我们的这个对称原理 啊。好，那么这个弯距图就是这样一个反对称的图形啊，好，这个题呢，应该说，嗯，不是太难啊， 好，所以以后我们画图的时候呢，嗯，如果这个和载图是对称的，可以考虑利用对称性来画图啊，这样呢，我们的画图过程也可以得到简化啊，好，这是这样一个题，好，我们再看啊，这样一个题，这个题呢，稍微 复杂一些啊，他是一个外深粮，那么第一步呢，我们也是先求制作返利啊，求制作返利呢，我们比如说假设二 a 这个 ffa 向上， fb 呢，也是向上的啊，然后呢，我们求制作返利，大家一定要 记住，最好是用立句防城，比如说对 b 点取句求 fa， 对 a 点取句求 fb， 这样呢，不要连力啊，否则连力的话呢，容，如果一个错了，另外一个也容易出现错误，然后球完以后呢，你再用外方向的投影方程来教和这个球的反力是否正确，然后你再接着往下画图 啊，否则你画到最后你发现错了，还得从头来啊。那么求知返利这个过程，我们就在这不讲了啊，我就直接 给大家把执法力写出来啊，那么求出来为证的，说明他实际方向都是向上的啊。好，我们重点呢，就是给大家讲这个话，呃，简历图和玩具图 我们前面给大家说过，根据这个微风关系定型，好，那我们现在来看一下每一段他的简历图和弯地图是什么形状的啊？好，首先我们看一下 ca 段和 db 段， 属于无核载的断啊，属于无核载的断，因此呢，他的简历图应该是水平线，是吧，根据我们的部分关系，那么弯距图那就是斜直线 啊，那么 a 地段他的减，他这个核散呢？他是一个军部核散，而且是 负的，是吧？按照我们前面的规定，他是向下的，所以说这一段呢，简历图应该是斜直线，而且从左向右是向下斜的，也就是说负斜率啊，弯距 图应该是一个抛物线啊，开口向上的抛物线，好基本的形状，我们都知道了啊，那么下面呢，咱们就来画图啊，咱们就来画图，我们看简历图怎么画 啊？简历图怎么画，我们可以分段来进行分析啊。分段来进行分析，我先来看一下啊，咱们这个图怎么是怎么画出来的啊？ 也是画一条轴线， c 点是不是有个向下子里，是吧，我们就向下图变图片多少呢？看上面和在图是三前牛顿啊，那我们就向下图变三前牛顿啊， 好，然后呢？呃， ca 段无何彩钢，咱分析过了，水平线，水平线啊，然后到了这个， 呃，制作出呢，他有个向上的 fa， 意思咱们要向上图片，这图片的这个值呢？就应该是 fa 的值啊，这个是 fa 的值，那么你下边知道是多少了？我们 fa 刚才计算出来了，是不是上面这个 之也就知道了，那也就说我们这个三钱牛顿啊，是 a 洁面，左侧是三钱牛顿，那么 a 洁面的右侧的简历值给大家讲方法啊，他就应该等于什么呢？就等于我们 fa 减去三千牛顿，对吧？所以这样呢，上面这个值也就知道了，好，然后呢， ad 断不说是个斜直线吗？那么这个斜直线到底 斜到什么位置呢？是不是需要确定一下地界面的简历，这个地偶呢，不影响我们的简历啊，不影响我们的简历，那么这个时候你可以根据地弊段 啊， db 段我们分析过了，他的简历图一定是一个长数水平线，那么是谁呢？实际上你就看这个 fb 就行了，我们最终你看，画到 b 洁面以后，一定是向上图片图片的零上这个零点去，所以说呢，这个 db 段的简历一定是一个副的啊，一定是一个副的 fb 是吧你否则的话，你无法从下边向上图片到轴线上去，以此呢， db 段的简历一定是在轴线的下侧啊，那么 这个时候这不 d 洁面的简历不就知道了吗？所以说 d 洁面的简历他就是 fb， 然后 db 段就这样一条水平线啊，然后呢？呃， ad 段， 那么就相连就可以了，相连就可以了啊，然后呢，标上正符号，下边是负的啊，下边是负的，上面是正的。建立图就这么画出来的啊，好，我下面我把这个呃建立图呢给出来啊，就就是这样的啊， 你看这个，看， a 只做处啊， a 只做处，下面呢是三牵牛顿，这是 a 只做左侧的简历是吧？上面四点二呢，是 a 只做右侧的简历，总的值四点二加三，这就是 fa 是吧，这就是 fa。 好，简历图就画完了啊，那么弯距图怎么画呢？我们画弯距图呢，实际上我们可以先求啊各控制点的弯距值，我这里也是给大家讲一下方法啊，讲一下方法， 那么这个玩具玩具图怎么画出来呢？我们也是你画一条轴线啊。嗯，找这么几个控制点， c 点 a 点 d 洁面呢，其实你找到左侧了，右侧咱图片就行了，然后 b 点哈， c 点属于一个自由端，没有外力偶啊，没有外力偶是 mc 呢，是不是应该等于零，对吧？好，那么 a 洁面的玩具等于什么呢？你就直接用四看和载图啊，左上角和载图直接用三千牛顿乘上 一米就行了，是吧？那么显然呢，他应该是上边手拉的啊，这个单位我这就不写了，前一吨米啊，这是上边手拉的对吧？上边手是这个手拉边，一定要知道哈。好，那么第一洁面， 那么 d 界面是让我知道左侧右侧就知道了，或者是反过来，我知道 d 这个 d 界面，这个利用做一下右侧的，那么左侧也应该反反着这个图片也能知道啊。好，那么我们先看一下， a 点是为零啊，这个 b 界面玩具为零， 那么这个时候我求一下什么呢？我通过地洁面的右侧，哎，我来求地洁面右侧的剪这个弯距，这个时候比较好求，是吧？左侧的话呢，可能稍微复杂一点。他我，那么我们就看地洁面啊，看这 这个上面这个图哈，他视频等于 fb 呈上 db 之间的距离，对吧？那么我这个力是向上的，对 d 界面 取句的话呢，他是一个逆时针的，那么我这个力是在地洁面的右侧，咱不是左睡右腻弯距为正吗？所以说呢，地洁面右侧的弯距啊，应该就是 f b 乘上一米，显然呢，是正的，那就是下侧手拉的，只要你知道了这几点，这个图就可以画了啊，然后第几面左侧咱们反着图变就行了啊。好，那你比如说，呃， a 点 c 点是为零，是吧？ 好，我们把它把这几个呢都表示的图当中啊， c 点是为零啊。 a 洁面的弯距是上边是 手拉的，好，画上边啊，画上边，那么 ac 段眉眉和仔直接画实线就行了，画实线就行了啊，好，然后呢？ b 点也为零，然后地截面的右侧是下边受拉的， 下侧收拉的，我画到下侧啊，好，然后地地段也可以直接连实线，是吧？因为何在？好，那么这个时候这个地结面左侧怎么办呢？ 你想象一下，如果我们要是这个从左向右的画的话呢，从左向右画一定是什么呢？ 呃，从左，从地界面的左侧，我要向右侧图片，这是一个顺时针的六千牛顿米的理由，一定是向下图片的，就我从地界面的，也就是说 我们 md 右侧的玩具上一个是等于 md 左侧的玩具加上这个六，就是这个六， 那么加上的话呢，我们按不是向下为证吗？所以从地结面左侧到右侧，一定是向下图变啊，一定是向下图变，那么你反过来，咱们现在反过来，你从地结面的右侧， 我是不应该向上图变图变到地截面的左侧，所以说地截面的左侧的弯距我们就可以求出来了 啊，所以这个地方咱们可以这样来处理啊。好，第一节面的左侧啊，你求出来以后呢？然后把这个 ad 段呢？先连于条须 虚直线，连一条虚直线，为什么呢？因为我们这段有君不和，在这段一定是叠加一个开口向上的抛物线，但这个抛线的集之点在哪呢？看简历图一定是在简历为零的点，那就是一点，那么一点这个距离上是可以求出来的， 是吧？根据三角形的比例关系是吧？四点二啊，比上这个三点八是吧？这就这两个三角形的比例关系，然后应该等于什么呢？比如说假设支持 x， 再比上什么呢？就是这个四减去 x 是吧？简单一个三星比的关系，把这个一点的位置就确定了，那么一点位置确定了以后，这段抛线的机制点的位置就确定了，那么我们画图的时候呢？哎，这个特征就出来了，从这个 减龄为零的这个点，我们抛物线斜率的符号开始发生变化，然后开始往上拐，好，这图形就出来了啊，那么这就最终的弯距图，那么这个抛物线及着点的这个值 就是一点的这个弯距如何来求呢？实际上你有两种方法，一点的位置知道了，直接可以根据上面的合载图取具，或者说呢，用我们上边简历图的面积来求啊，简历图的面积来求，那就说 m 一等于什么呢？看简历图，一个是三角形的面积，三角形的面积呢？三角形面积是一个正面积，是吧？那他应该是产生正玩具在减去什么呢？ 这个巨型的这个负面就可以了，就可以了啊，这个玩具图就这点的玩具纸就知道了啊，最后的玩具图就出来了 啊，所以我们最后的弯距图呢，就是呃，这样这个画出来的啊，我们能把这个图形呢给出来啊，标准的刚才呢是我们的分析的过程啊，好，我们看这个图， 大家看这个图形就是这么画出来的啊，就这么画出来的，看啊，嗯，这个塞一段是吧？ 斜直线，然后这个 db 段也是斜直线啊，斜直线，然后，呃，关键就是什么呢？ a 洁面到 d 洁面的左侧 啊，你先连一条直线啊，先连一条直线，再叠加抛线，抛线的机支点啊，抛线的机支点在这个简历为零的位置啊，那么这个这个玩具是可以求出来的。 另外呢，就是这个地洁面这个图片啊，地洁面的这个图片啊，我再把这个地方呢再给大家讲一下这个图片怎么来的啊？ 哎，我们这个你可以这样，也可以求一下第洁面左侧的简历，第洁面左侧进来看上面和在图啊，左侧的简历 我们也可以用右边的这个 fb 和这个集中六来求，是吧？那是不是应该等于 fb 乘上一米，对吧？ 把这个产生下面收拉的这个玩具啊，减去谁呢？减去这个利哦利偶就行了，因为我们说左顺右逆吗？是吧？那么地洁面的我求地洁面左侧的玩具， 那我这个六是在这个地，是在他的这个洁面的右侧，那么他顺时针的时候就要减去了，首先减去六，这个得出来，把我们这法例带进去，就是负的二点二，负的二点二，那么负的代表是哪受拉呢？上边受拉的 好，就是我们下边啊，左下角这个图，这个二点二，然后从二点二呢，向右图变，是吧？向右图变，这不有个顺着的理由吗？从左向右图变，遇到顺着没有向下图变好，二点二， 那么图片值是多少？六，然后下来三点八，所以这个三点八是 d 洁面右侧的啊，二点二是 d 洁面左侧的，然后必点是为零，连直线就行了啊，所以这个玩具图呢，就就出来了，所以我们归淡下画玩具图的方法哈，你就按不就班的把各个控制点的弯距值求出来， 然后呢，表示在图当中相邻两点连直线没有何在？划实线， 你看 ca 段， db 段是吧？有何在？像我们 ad 段啊，从 a 到 d 的这个左侧啊，有何在？我们在叠加上相应何在，再把它当成这段，当成减脂粮。 你看我这个一连，你看这边是三，这不是二点二连不是一条虚线吗？连完以后把它作为一个基准线在第，就是这样一个 梯形，好，再叠加什么呢？这样一个抛物线就可以了，是吧？这就咱们前面不是讲叠加法做玩具图的方法吗？对不对？好，这就是这个图的画法啊。 好，我们后面呢，还有给大家推出这个画这个玩具图简图的这个题目。好，同学们再见。

大家好，我是土木光头强，欢迎来到我的材料留学课，通过之前课程的讲解呢，已经为大家展示了如何用内力方程的方式绘制两样的简历图以及玩具图。 那虽然这种方式啊，比较好理解，但是呢，如果梁上的核载比较多，我们再用内力方程的方式啊，绘制简历图，玩具图的时候就需要分很多段，那具体的工作量呢，也是非常大的， 实际应用的时候呢，我们其实并不是用内里方程的方式来绘制简历图和玩具图，而是用核载、简历弯距他们三者之间的一个微积分关系来进行绘制。那在具体讲解这样一个绘制方式之前呢，我们先要简单了解一下核载、简历弯距他们之间的这样一个微积分关系。 那首先呢，我们选择这样一个简单的这样一个梁的形式，那在这样一个梁上，它作用 加一个集中立友这样的一个分布和载，注意啊，分布和载和我们前面讲的军部和载不一样啊，那分布和载呢，相当于说在这样的这样某一个段内，他和载是连续分布的，但是大小呢，并不是一样的， 均不合展的是大小一样的啊，我们为了更普遍选择的是一个分布合展寓意着在某一段内，他的合展并不是一样的啊，当然方向呢，也是我们任意选的哈，还有作用的集中力批， 那大家可以简单想一下，如果对用于这么多核载，这才上面有三个核载，如果你要进行这样一个内力方程绘制的时候，他需要分一段，两段，三段，四段、五段，那你想会相应来说呢，应该是绘制成一个五段的一个 加一个分段函数，那绘制起来这工作量会非常大哈，因此呢，我们其实实际上并不用那里方程来进行绘制， 但是内立方程绘制简历图、关系图的方式呢，也要求大家掌握啊，作为一个基本知识点需要大家掌握，那我们再看一下啊，他们三者和载简历弯距，他们之间的一个微积分关系，那么对应于这样的一个梁， 假设呢，我们在这样一个分布合窄这一段，哎，分布合窄一段，哎，把它呢取出一个小段，比如说在他这个位置砍一刀，在这个位置砍一刀，然后呢取出他中间的所分离出这一小段，哎，这一小段作为分离体呢来进行分析。 那么取出来之后呢，我把它放大，哎，放大到这样的一个位置，放大到这样一个位置，希望大家能对应好，那注意我要求的什么呢？取的这两个所相邻的这两个洁面，这两个洁面距离呀，是非常小的来，非常小的，假设这个距离的这样一个长度呢， 是 d x， 距离左端的这样一个位置呢，是 x 啊，是 x 这样一个位置，那首先这是表示一个小微圆，哎，小微圆，这是一个 d x， 哎， d x， 那虽然在这样的一个位置上，他是一个分布合载，当然了，如果你这两个界面他距离非常近的话，我们是不是可以近似看成这一段位置，他的分布合载是均匀分布的，哎，那么这个呢，就把这样一个 这个分布和窄，在这一段内用一个均不和窄 q x 代表小 q x 啊，那这个呢，是不是就是和窄呀？然后说对应的，我说取出来这个分离体这个红色的位置，这个红色的位置是不是相当于我我分别砍开的两个界面， 看这两个洁面，那这个是左侧洁面，这个是右侧洁面，那所对应的，在这两个洁面上所反映出来的或暴露出来的内力呢？简单给大家标注出来， 那么这个简历，比如说这个界面，他的外侧是不左边啊，对不对？先画一个与界面相平行的线，那相对于这个节目来说，是不向上指才是一个顺时针转动趋势， 对不对？哎，然后呢，这个洁面这个左侧，这个洁面对于这个分离体段是不是左侧，那么左侧的弯距应该是左顺右逆为正，所以说这个弯距呢，我假设成是顺身方向，那么对于这个分离体的右段，哎，好了，看这个洁面的时候， 还是先画一个与截面相平行线，眼线平行线，那么两个外侧画一点，那么在上边取一点，我们来看一下， 是不只有这个简历向下指的时候，才是绕着这个界面上的点，是顺时针转动趋势，哎，我们假设的这是正的简历方向，右侧界面的正的简历方向，而右侧界面弯距左顺右逆为正，那么在这个右侧面呢，我要先假设他的这样一个 弯距是逆时针方向的，没逆时针方向的，那这次呢，我对这样一个取出来的分离体给大家进行个数理分析，然后呢大家要注意一下这个符号的表示， 哎，符号的表示，那么假设左端的他的这样一个弯距呢？是 mx， 为什么有 x 呢？因为在前面已经输了，这样一个简历，和弯距他都是一个方程，对不对？随着你所选的截面位置不同，他的数值也不一样，他是一个关于 x 的函数。那么在这里边弯距呢，我就用 mx 来表示， 这个简历呢，就用秀 x 来表示，那以左端为基准，右端的简简历和弯距他是有一定变化的，那么我们用什么方式表示呢？我们用这样一个铮亮的形式来表示，就是相对于左端，他的弯距呢，增加了多少？那可能从符号大家不太好理解，比如说，哎， 我教大家一个身高，比如说我的身高，我的身高是一米八一，哎，一米八一，那如果说你问我身高多少哎，那我就不说我是一米八一，我说我是一百八加一，哎，那他说反应的意思是不是也是一，那个这个一米八一呀，但是呢，哎，那个一表示的就相对于这个应八，哎 多出来的那一份增量来源。当然了，如果说我一米七九，哎，我也可以用这种方式来表示，那就说我多高呢？我说一米八减一，那就减一， 所以说这个增量啊，他是可以正可以负的，对吧？我们只不过把它称之为变化量，叫做一个增量，那么这就是一个表示方式，就是相对于左侧的这样一个弯距，右侧的弯距，用一个增量的形式， 以左侧为基准，加上一个锃亮的形式来表示。同理，简历一样，以左侧的简历为基准，右侧的简历啊，用这 这种一个这个 q x 加上一个 q x 的一个增量的形式来表示。那注意呢，这个 d m x 和 d q x， 这是弯距的增量，这是简历的增量。好了，大家明确了这样一个受力分析图之后，接下来对这样一个受力分析体呢，对它进行 平衡方程的这样一个求解平方，求解数值方向的力的投影的代数和为零，我们来看一下这个上边数值方向力有谁？ 首先朝某一个方向上立投影的代数和为零的时候，大家要特别注意，我们是不管立有的对不对？所以说不管这个 m x 和右侧的这个 m x 加 b m x， 而只看什么呢？看左侧界面的简历是向上指的，向上指的，那应该是 这个 q x， 然后加上注意这地方是不是还有分布和窄呀？分布和窄是尾向上指的 来发向上指的，那什么叫这是均不合展啊？均不合展，那他说产生力的效果是不是这样一个均不合，在要乘以这一段的长度，这一段长度是 d x， 哎，那他说产生的向上的力的作用效果就是 q x 乘以这样一个 d x， 哎，这是向上的力， 那等于什么？等于向下的力，向下的力呢？就是右侧面的简历，那么他向下指的，我们就把这个直接写出来，那写出来左侧的向上的等于向下的好了，那这是列平方程，然后观察这个平方程，这个简历和这个简历是不是就掉了，对不对？哎，就掉了，那对应的这一项是什么？是 两个界面所对应的简历的增量，而这个是什么？是这样一个杆段的长度，我如果把这个 ds 除过来，哎，除过来，那这个 dqi 这个增增量，简历的增量 除以 e x 是是不是所代表的？就是这样一个简历方程的他的一个倒数的关系，这就是我们数学里边那个倒数的含义，对不对？哎，倒数的含义在这样一个范围之内，他的这样一个简历的变化量，哎，也除以这样长度，哎，就是简历的倒数。那么通过这样的一个推导，我们知道了，哎， 简历方程的一阶倒数是否和这样一个分布和载这个小 qx 是有关系的？那那么这就推出来了我们这样一个和载与简历他们之间的一个微积分关系，简历的一阶倒数等于什么？等于分布和载， 那这个方程用完之后，我们还有一个平方程是取句的，对不对？取句的我们不取水平方向的，没有，没有水平方向立马我们不取，我们取什么呢？哎，取这样一个对某一点取句，那对哪一点取句呢？还是对哪一点都取 行，但是呢，我选择了右侧洁面上的点，哎，比如说在右侧洁面，我选个小 c 点啊，假设我对这个小 c 点取句，那为什么选右侧洁面？当然你选左侧洁面也可以选右侧洁面，就是因为 你选右侧洁面的小 c 点的时候，右侧洁面的这个简历，哎，这个长的这个简历，他对这个 c 点是没有距的，因为这个简历实际上是在这个面内的，对不对？他是没有例句的，那因为他表示方式比较长，他要没有例句的话是不写的，比较好写，那我就 选择右侧节面这个小 c 点，哎，那就是曲距点啊，曲距点，那我们来看一下这个分离体上都谁对这个 c 点有距，我们先看顺时针的，哎，首先是不是有这个 mx 啊，对不对？ mx 他就是一个顺时针转动趋势，不管你对哪一点曲距啊，都是顺时针的，哎，这是 mx。 然后左 左侧前面这个简历对 c 点有没有例句？有，因为他向上指相当于到对应于 c 点来，是一个顺时针的转动趋势，并且呢， 他的利弊是 d x， 那这样一个左侧的这样一个简历对 c 点的这样一个例句，就是 q x 乘以 d x， 哎，为什么我没加符号，我只不过把顺时能放在一边，逆时能放在一边，哎，一样的啊，这个前面已经给大家强调过， 然后别着急，大家在列平衡方程的时候，游戏做力学问题一定要认真仔细，别漏力。那这两个用完了，哎呀，别忘了什么叫君不可载呀，对不对？君不可载他也是有力的效果的，前面说了，他是多大的力呢？是 q x q x 乘以 d x 这么大的 d， 它的合力的重点在哪啊？是不是在这个中间呢？还有画的有点歪啊，是不就是 小 q x 乘以 d x， 大力就在中间，那它对于 c 点来说，它的这个力 b 是不？这段长度是不二分之 d x， 哎，那相当于说 q 乘以 d x 这么大力，再乘以二分之 b x， 就是均不合在对这个小 c 点所产生的顺时针的这样一个例句。 顺身例句好了，右侧节面的。刚才说了，简历对这个右侧节面的简历对 c 点是没有例句的，但是这样一个右侧节面的弯距对他是对这个 c 点是有这个 这个转向的啊。转向效果，它是个逆时针的，我把它放在等号的右侧，放在等号的右侧，哎，那么这呢就是对 c 点列出合力距的这样一个平衡方程，那在这样的平衡方程里边，大家不难看出，这里边的这个 m 和这个 mx 是不约掉了，对不对？哎，约掉了。 但是呢，我们看这一项，根据下边这个结论，我发现这一项也没有了。为什么这一项没有了？那注意强调一下，我们刚才说选的这两个相邻近的，讲洁面，是不是这个 d x 要非常小啊？意味着它是不是趋近于零的， 对不对？还要区均一零的，那就意味着在我们数学里边，一个数区均零的话，我们是不把它叫做无穷小， 对不对？哎，就是无穷小的概念，有人说你看 d x 是一个无穷小的概念，那么 d x 再乘一个 d x， 两个无穷小相相乘叫什么？是不是叫做高阶无穷小啊？ 对不对？高阶无穷小，那什么叫做高阶无穷小？我们只是在数学里边碰到过这么个概念，那什么叫高阶无穷小？那就意味着本来就是一个趋近于零的数，你再给他平方一下，那就更趋近于零了，对不对？ 那我们在进行参与计算的时候，我们是不可以忽略掉整个这一个区域零这一项的影响，所以说由于他是高阶无影响的，进行计算的时候，我们就不考虑这一项的影响给他，直接认为他是没有了， 没有了，哎，是无有，无了，是吧？哎，无了。那这时候这个平方格里边这一项，这一项约掉了，这一项不考虑了。那么自从什么了，是不？就算 q x 乘以 d x 等于 m x， 同样把这个 d x 再除过来，是不就等于 d m x 除以 d x 等于什么？它俩等于的是 q x q x 什么是简历方程？ mx 什么是弯距方程？那有这样的一个式子说明什么？说明弯距方程的一阶倒数。弯距方程的一阶倒数，它等于什么？等于的是简历方， 弯距方程呢？一直倒数等于呢，就是简历方程，那因此呢，通过这样的一个简单的取出分离结，通过平方程的这样一个推导，我们得出了啊，核载简历弯距，他们三者之间的微积分关系是什么关系？ 简历的一跌倒数等于何等？弯距的一跌倒数等于简历，哎，那么这个呢，就是他们三者之间的一个危机分关系，哎，简单的把它总结在这里，就是弯距的二跌倒数，哎，等于分布合载，哎，那么弯距的一跌倒数等于这样一个 简历这个方程来简历方程，那这个呢，就是我们后续绘制这样一个复杂喝载状况下简历图和班级图的一个最根本的这样一个依据和原理。那这样的一个推导关系其实并不是特别难哈，更多的就是利用这样一个平衡方程来进行推导。 各位同学，课下的时候呢，希望大家花些时间把这样的一个过程呢进行一个完美和整理。 那通过这样一个微积分关系，哎，我们总结出来了这样一个绘制简历图和弯距图的这样一些方法，那这样的一个思维导图，哎，大家呢，现在可以先不用看哈，那对应的这样一个，大家如果在屏幕上看不太清楚的时候，可以在下边的这样一个 这个视频介绍里边进行相应的一个链接下载，来链接下载，我把这样一个图片呢，已经用链接下载形式放在了这个下边的这样一个课程介绍，哎，那部分大家可以自行下载，那具体的我们会通过后边的这样一个立体讲解，来帮大家一步一步看一下这些啊。一个 思维导图所对应的这样一个简历图，班级图，它的一个绘制规律。刚开始绘制的时候呢，大家肯定会觉得比较麻烦，而且不太好理解， 也记不住很多这么多的条，但是呢，这一部分大家只能通过一些题海战术，多做一些题来熟悉这样一个过程，你的这一部分如果熟悉好了，后面呢？哎，绘制会迎刃而解。再次强调，哎，这一部分绘制简历图和班级图的这样一个 这样一个题型，是在力学里边非常重要的，只要考材料力学的课程都会考到相应的内容，因此他必须掌握，哎，必须掌握，所以大家呢，先不用着急。哎，这个图呢，大家看不清，也不也不要紧，大家可以先下载去活跃起来，等到应用的时候，具体的慢慢用， 大家不用担心，只要你多做一些题，哎，肯花一些时间呢，肯定能掌握这部分内容。好了，本次课呢，就先为大家介绍到这里，更多精彩内容敬请关注土木光头强。

下面呢我们进行讲解的是材料力学的第二章，拉伸、压缩和剪切。 我们来看一下这一张的结构是怎么样的，因为这一张啊，内容很多，包括了我们这个啊三种应变形，变形形式，拉伸、压缩和减七。我们看一下内容的分布。第一节呢，讲的是轴向的拉伸与压缩的概念和实力， 许的就是我们拉伸和压缩呢，当然就是发生在轴向的了。那么第二节呢，讲的就是说轴向和拉伸和压缩时，横截面上的内力和硬力是怎样分布的。 那么第三节呢，简单就是说当这个直杆他在轴向拉伸和压缩的时候，斜节面上的应力是怎样分布的？如果我们分析的 这个这个内力的这个洁面不是垂直于他的轴线，而是一个斜着的话，这样的洁面上的应力是怎样求的呢？就是在第三节讲，第四节呢，会讲的是材料拉伸时的力学性能。 第五节呢，会讲到材料压缩时的力学性。然后呢我们会讲一个构件，什么叫做他失效了，那么什么叫做安全因素，什么叫做？而他的强度呢？又是怎样计算的？ 第八节呢，要讲的就是说轴向拉伸或压缩时，这个东西的这个构建的变形是什么样的？前面呢我们一直在分析的是受力。最后呢第八节呢，讲的就是变形。第九节呢，讲的就是说轴向拉伸或者压缩时的应变能。第十 节呢，讲的就是拉伸压缩的超静静问题，如果呀，这个拉压杆他不是一个静静系统，而是一个超静静系统了，这样的问题要如何分析呢？第十一节我们要讲的就是温度应力和装载应力， 这两种应力是什么意思呢？听上去很高深的样子。在第十一节呢，我们就会分析他第十二节应力集中的概念，我们经常会说呀，这个地方应力集中了，那他到底是什么意思呢？ 我们会给一个非常详细的讲述。最后呢我们用一节来讲一下剪切和挤压的使用计算好了，下面呢我们就一节一节来开始讲解。 第一节我们要讲的是轴向拉伸和压缩的概念，什么叫做轴向拉伸和压缩呢？比如说这样的一个行架结构，这是我们非常常见的行架结构， 那么我们知道这每一根杆呢，其实都是一个案例杆，那么他都会受受到的是轴线，这根杆的两端的重力呢，一定是沿着这根轴这根杆的轴线的， 这样的杆呢就叫做轴向的拉压杆。那么他发他如果要发生变形的话呢，如果他受压，他就会沿着这个轴向压缩，如果他受拉就会沿着这个轴线伸长， 还有这样的一根吊车的这样一个吊臂，那么他在这个重物的力的自动下呢，就会发生压缩，因为他受到一个沿着这个 这根悬臂的这样的一个压力的作用，会使他缩短。 那么我们来看一下轴向拉压杆，他的受力特点和变形特点是什么样的呢？ 他受力的就是说他受的力的这个作用，在感情上的外力的合力呢，他们的作用线都是和感见的轴线重合的，只有这样的感见呢才叫做拉压杆。那么 他的变形的特点呢，就是说杆在他变形也一定是沿着轴线方向上的伸长或者是缩短，如果是拉的话呢，那就是伸长，如果这个杆受到的是压力的话呢，那就是缩短。 我们来看一下拉压杆的受力图，如果这是一根杆，你要是拉他的话呢，他的 这个虚线就是他变形之后，他就会伸长，同时呢洁面积，因为这根这根杆他的体积要守恒，那么洁面积就会缩小。同样这是一根杆，如果两端给他是一个压力的话呢，他就会变成虚线的，这样他就会缩短，同时呢洁面积也会增大。 那么下面呢，我们来讨论一下这样的一个问题，说如图啊，这四个杆件中，哪些杆件是轴向的拉压杆呢？ 第一个杆件一端是固定端，然后呢我在他的轴线下方一点，给他一个轴向的力。第二根杆呢，是这根杆的两端都给作用在轴线上的力。第三个第三根杆呢，一端固定，另一端呢受到了一个斜向 下方向的这样的一个集中力。最后这根杆呢，他的两端分别说的是分部的一个力和一个集中力，那我们看一下吧，第一根杆，按照我们这个轴向拉压杆的定义， 这根杆杆他受到了合力的这个方向呢，合力的作用线呢，一定要和他的轴线是 重合的，那么我们看一下。第一，第一个，如果他收到了这个力， f 是偏下一点的话，那么那面的这个力啊，同力也应该是和他一起偏下一点， 所以说他受到这个力的合力的作用线呢，并不是和他的轴线重合的，而是平行的，所以说第一个就不是，那我们再来看一下第二个，第二种情况 很明显吧，这两侧的这两个集中力都是作用在他这个轴线上的，所以说他这个合力外力的作用线呢，和他这个轴线是平行的，是平行且重合的，所以 b 是可以的。第三个呢，如果这个 f 有一个向下的分量，那这面 嗯也肯定是跟他平行的这样，但是呢，既然 f 他的作用线已经跟轴线不再不是重合的了，所以说 c 也不可以。 那么看第四个吧。第四个他虽然说左侧是一个分布力，不是一个集中力，但是如果对这个这根杆进行受力分析的话，这两段的力呀，一定是平衡的，那么也就是说这根分布力呢，可以等效成 一个作用在这根轴线上的一个集中力，而他的作用线呢，也一定是在这根轴线上，所以说地也是可以的，他也可以认为是一根轴向的拉压杆。 下面呢，我们来讲第二讲轴向拉伸或者是压缩时候的这个横截面上的内力和硬力是怎样求的。我们来看一下， 还是说这样的一根轴向的拉伸的这样的一根杆件，我们想求他的内部 m m 这个洁面上的内力是怎怎样来求的呢？ 那么我们回忆一下，还是运用洁面法，用这根洁面将这根杆切成两部分，然后我们分别取任何一段来进行受力分析都可以。如果我们取左侧的这一部分的话呢，那么对他受力有外力，还有 这根洁面上的这个内力 fn 要取右面这部这根杆子也同样是受到了外力 f 和这个内力 fn 的作用，那么对任何一个部分作为研究对象进行受力分析的话呢，我们都可以得到 这个 x 方向上的受力平衡，那么 fn 就等于 f。 那么具体的洁面法求内力的步骤呢，还是这样四步，第一步就是用假想的一个沿着 m m 的这个横截面呢，将这根杆切开。第二部分呢，就是留下 左右两侧的任何一侧作为研究对象。第三步呢，就是将气趣的部分对留下部分的作用呢，用内力来代替。最后一步呢，就是对研究对象呢进行列解平衡方程，求出这个 轴向的内力，他的值是多少。然后呢，我们来看一下什么叫叫叫做轴力。轴力呢，举的就是说我们这个拉压杆在洁面上的内力，他就叫做轴力，因为他是沿着这个杆的轴线方向的，所以他就叫做轴力。 那么由于外力的作用线呢，与杆件的轴线是重合的，所以说内力的作用线呢，也一定是和杆件的轴线重合的，这种力呢就称为轴力，就是我们刚才求解的这个 轴向拉压杆他的受力，这就是轴力。那么轴力呢，也分为正负两种，我们规定正的这个轴力呢，就是拉力，富的这个轴力呢就是压力。那么什么叫做轴力图呢？这个是我们经常要做的轴力图，他就是会 这个轴里沿着杆件的轴线的变化，比如说就是在这样的一根轴上，这根轴的长度呢，就表示的是这根杆他的这个长度的分布， 而这根杆的不同的啊，不同的段上啊，因为他的这个轴粒的正负是不一样的，我们就用正负来表示成这样的一个图像，正的呢就画在这个 x 轴的上面， 负的呢就画在 x 轴的下面，表示的是压力，正的就是拉力，然后呢用一些啊平行的这样竖线 做好，把这个图线呢封闭起来，这样做好的呢，横轴就是 x 轴这根杆的坐标的分布，而纵轴呢就是这个轴里的大小，牵牛，然后呢我们要在这个 轴力图上的这个右侧呢，标好这个力的绝对值的大小，比如说这是一个十十千牛的拉力，二十五千牛的拉力和十千牛的压力，我们就这样做好了， 然后我们看一下这道立体吧，来讲一下怎么样画轴里图，这是一根杆， 我们知道这是一根等洁面的直杆，等直杆，那么他受到了呢三个外力的作，四个外力的作用， f 一， f 二， f 三， f 四在这画着呢方向呢也由途中给出了 什么，因为呢 f 一二二三四他们的大小呢是变化的，但是呢对他们求和应该是相应的，能够使这个 这根杆平衡，看我们的 f 一加上 f 三是四十五牵牛， f 二加上 f 四呢也是四十五牵牛，他们四个力的作用呢使这根杆平衡了，但是因为他们的分部的关系，就会使这根杆尖的内部的内力啊，是分段的，是不均衡的。 那么让我们画图，画画出呢这根杆尖的轴力图，那么要画出轴力图，我们就要先求出这根杆尖每一部分他的他的内力是怎样分布的，我们才可以画出这个图， 那么我们可以看一下，因为呀这些力的看， f 一重在是在 a 界面， f 二呢？重在 b 界面， f 三是 c 界面， f 四呢？是啊， d 界面。那么我们就可以很很明显的可以 发现呢，就是说在 ab 的这一段内，他的轴力呢，应，应该他的内力应该是一个力，在 bc 这一段的内力呢，应该是一样的，因为我在 bc 段的，我在 bc 段的任何一个点洁面一节之后呢，两侧的受力呢，都是一定的。 而如果我在 ab 段和在 bc 段接一下呢，这两这两个洁面的两侧的受力就是不一样的。所以说呀，这个杆的三段就表示了说我应该有三种不同的内力， 在这个杆的受力分受力中，我们就可以将这个杆分成三段，那么我就取每一段中的一个洁面，用这一个洁面来代表这一个段中的这个内力的分布。比如说在 ab 段中，我取了一个洁面，一 一，那么用这个一一将这个杆揭开之后，我取左侧来研究对象，那么我又用这个，嗯，二二 这个洁面将这个 bc 杆也给解开了，解开了之后呢，这是二二，之后呢，我取一二中间这部分作为研究对象， 然后呢，我又用三三这个洁面将 cd 杆解开了，解开之后呢，我取右侧的这一小段小短部分作为我的研究对象， 那么我们现在就去每一个研究对象进行受力分析，然后呢，得到我们这个洁面上的这个内力的大小，对于第一部分的这一个小。