洋葱学院30天精研班是什么
粉丝4.3万获赞14.8万
相关视频
 01:58查看AI文稿AI文稿
01:58查看AI文稿AI文稿学了这么多年数学,我们见过了各种各样的数,比如整数、分数、小数,还有各种各样的图形,比如圆、正方形、长方体、圆锥等等。 一眼看过去,树是树,图形是图形,两边好像没什么关系,可实际上,树与图形之间有着非同一般的联系。 解决问题时,如果树形结合,双剑合臂,常常可以事半功倍。比如有的时候,图形能帮助我们了解树的含义。就像刚学分数的时候, 如果给你一个三分之二一下,可能很难反应过来他到底表示啥意思。但如果结合图形,就简单多了,画个圆,把它 平均分成三份,取其中的两份,一眼就能看出来分数三分之二表示的是什么意思。 还有些时候,图形能更好的展示数量关系,比如这种谁比谁多几分之几的问题。光是读题常常搞不明白数量关系,可要是画个线段图,谁多谁少,谁占谁的几分之几,直接就一目了然了。 当然,反过来,竖眼能帮助我们更好的看清图形。就拿这两个角来说吧,如果让你比较他们的大小,你能一眼看出来吗?恐怕很难吧。 但如果我们用树把他们的角度标出来,谁大谁小,就一清二楚了。看了 这么多例子,你对竖行结合的好处是不是有了更多体会呢?那在这一张里,我们就会和狗蛋一起用竖行结合的方法来挑战两道繁琐无比的计算问题。还等什么呢?一起来看看吧!
287洋葱学园App 00:28查看AI文稿AI文稿
00:28查看AI文稿AI文稿等于二,外就等于四,当孩子等于三十呢,外就等于三,等等等等等等等。 这个表格里的 x 和 y 对应的值都是满足条件的,他们都可以让等式成立的。 狗蛋终于明白了,并不是二人一次方程很诡异的,而是二人一次方程和姐很诡异啊,有无数多组,而且很有整数。
147教数学的吴老师 05:25查看AI文稿AI文稿
05:25查看AI文稿AI文稿在这个视频里,我们要学的概念是立方根,关于他有个古老的传说。话说公元前四百二十九年,在古希腊的提罗岛发生了一场大瘟疫,死了好多人。正当疫情肆虐的时候,岛上的居民去供奉阿波罗的神庙,请求神的庇护。 寺庙里祭司心想,请大神帮忙,总要表现点诚意吧。这样吧,供奉阿波罗的祭坛是个立方体,如果你们重新做一个,把他的体积扩大一倍,那阿波罗肯定很开心,瘟疫也就拜拜了。 虽然这看起来明显就是变相要钱的行为,不过束手无策,岛民们只能尝试把立方体的体积扩大一倍。一开始他们把立方体的边长从一变成了二,结果结果又死地骗人。原因是因为正方体的体积等于边长的立方,所以把边长扩大一倍后,他的体积就从一的立 变成了二的立方,也就是原来体积的八倍,和把体积扩大一倍的条件不符。不过你可别觉得古希腊人是笨死的,这问题没那么简单,请你自己想想。一个体积为 x 立方体的边长怎么表示呢? 算立方体的体积需要求边长的立方,如果体积为八的话,我们知道是二的立方得来的,但是要做一个体积为二的积碳,就等于要去找一个立方后等于二的数字。 岛民们和你一样,都不知道是多少,于是就去找了当时古希腊最聪明的人柏拉图。柏拉图 接到任务后,和他的学生研究了半天,后来发现很难通过尺规作图做出一个体积为原来两倍的立方体。而这个谜题也流传了上千年,成了尺规作图三大难题其中的被立方问题。 这个故事的本质和前面算入平方根的问题很像。对于一个正方形,他的边长和面积之间是通过平方和开平方相互转换的, 那立方体的边长和他的体积该怎么转换呢?从边长到体积要立方,那以此类推,从体积求边长就要把立方后的结果还原,这个过程我们就叫他开立方。 体积为八的立方体的边长是二,也就是说八开立方后等于二。那么请你判断一下,如果一个体积为二十七的立方体,它的边长是多少呢? 求他的边长就等于要将二十七开立方。求一个立方等于二十七的数字,那三三得九三九二十七,所以呢,这个数就等于三。这里再继续考你一下,参考 报一下前面平方根的定义。请问二十七开立方后得到的三这个数字该叫他什么名字呢? 开平方的结果叫平方根,那开立方的结果自然就叫立方根嘛。三就是二十七的立方根,二就是八的立方根。选板蓝根的同学,请你自己洗洗睡吧。 话说表示一个数的算数平方根的时候,我们会用根号,现在要求立方根了,就也要有个符号吗? 但是重新发明一个又太麻烦,于是数学家就偷了个懒,把根号左上角加上三改装一下,叫做三次根号。作用不用我说你们也能猜到。三次根号用来求或者表示一个数的立方根。 那么请问一下,如何表示一千的立方根,以及他化减后等于多少呢? 答案是 c 求立方跟必须用三次根号,十乘十等于一百一百,再乘十等于一千,所以呢,答案是三次根号下一千等于十。 通过三次根号求立方根的运算和用根号求算出平方根是很相似。同样的,我们也可以求分数的立方根或小数的立方根。比如三次根号下六十四分之二十七就等于四分之三,而三次根号下零点零零一就等于零点一,这里要注意数清小数点。 学平方根的时候,有个概念叫完全平方数,就像四、九、十六、二十五这些数的平方根是整数, 同样的,也有很多数的立方根也是整数。这里呢,我们需要认识一些常见的可以化简为整数的立方根,比如八、二十七、六十四、一百二十五、二百一十六和三百四十三这几个, 以免做题时碰到了手足无措。暂停在这里,以下你们互相认识,这里呢,尤其要注意一下六十四这个数,六十四开平方等于八,而开立方后呢,可以得到四。 了解了立方根和平方根他俩的相似之处后呢,我们再看一下他们之间一个重要的区别。首先是关于根号内的数字范围, 因为负数没有平方根,所以二次根号下的数都是大于等于零的。但是适应到立方跟这里就不一样了,因为负数的立方依旧是负数,比如负二的立方等于负八,那么负二就是负八的立方跟,同样的,负二七的立方跟就是负三, 也就是说负数也是有立方跟的。所以呢,你算一下负一百二十五的立方跟应该是多少?求负一百二十五的立方跟,就是三次根号下负一百二十五,答案呢是负五 负数不仅有立方跟,而且立方跟也是负数,同时零的立方跟等于零,这点和零的平方跟一样。 总结一下,所有实数都有立方根,并且也只有一个立方根,正数的立方根是正数,负数的立方根是负数,零的立方根是零。
671洋葱学园(贵港)服务中心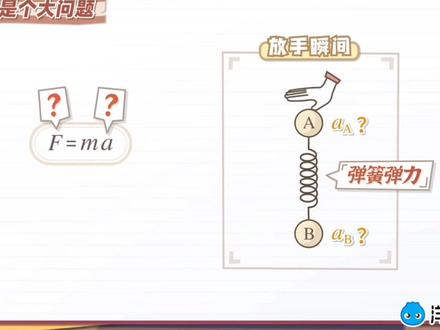 05:08查看AI文稿AI文稿
05:08查看AI文稿AI文稿嗨,同学们好,在学完牛顿第二定律之后,同学们应该都遇到过一类让人非常头疼的问题,很容易错。这类问题呢,大概长这样,两个小球啊,用弹簧连起来,用手拿着,俩球呢,都保持静止。这时候啊,突然把手放开,问,你放手瞬间,这两个球的加速度是多少? 求加速度可以用牛顿第二定律,这个不难想到,但问题是,很多同学不知道松手瞬间弹簧的弹力是多少,就求不出合理 f, 也就算不出加速度了。接下来呢,咱们就用这个例子讲一下这类问题的解法,听完你就知道了,这种题啊,真的不难,来看题吧。 题目呢,很简单,就是在问放手的瞬间,这两个球的加速度分别是多少?用牛顿第二定律,球加速度肯定是没毛病的,然而球公式里的这个合力啊,就得知道这根弹簧对他俩的弹力,松手的时候,弹簧的弹力是多少呢? 这就触及到咱们的芝士盲区了。不过呢,你也别急,咱们这节课呀,就是要解决这个问题,这个弹力怎么求呢?注意听啊,这个诀窍啊,就隐藏在弹簧的长度上,我们知道弹簧长度变化,弹簧的弹力就会变化,所以呢,我们可以通过观察弹簧的长度来判断弹簧的弹力。 接下来呢,我们就来实际演示一下这个过程,要注意观察弹簧的长度是怎么变化的哦。首先,我们把器材连接成题目中的样子,接下来放开手就行了,注意看弹簧的长度来,放手, 你看,这是放手瞬间,而这是放手前看出来了吗?放手的瞬间啊,弹簧的长度几乎是没有发生变化的,这件事啊,挺好理解,弹簧呢,无论是伸长还是缩短都需要时间嘛。长度啊,不会突然 变化,这也意味着弹簧弹力不会突变,这是一个非常重要的结论。但是这个结论啊,我们回到这道题里,弹簧弹力不会突变,所以啊,只要求出放手前的弹簧弹力,放手后的弹力呢,也就知道了。事不宜迟,赶紧来算一算, 放手前的弹簧弹力,很好算。对 b 做受力,分析,他受重力以及弹簧给他向上的拉力。因为 b 静止处于平衡状态,所以弹簧弹力就等于 mg, 弹簧弹力出出相等,所以 fna 也是 mg 得到了弹簧弹力,我们再回到放手的瞬间,就可以先求合力,再求加速度了。先做受力,分析, a 受重力以及向下的弹簧弹力, b 呢,和之前一样受重力和向上的弹簧弹力,这样合力就很容易得到了。 a 受到的合力是 mg 加 fna, b 呢,合力是 mg 减 fnb。 注意啊,关 的来了,弹簧弹力不突变,所以 fna fnb 还等于 mg 带入一算, a 的合力是向下的二, mgb 的合力是零。合力找到了,接下来算加速度,利用牛顿第二定律得到 a 的加速度是二 gb 的加速度呢,是零。答案,选 d 加速度啊,是二 g 和零。根据这个结果,放手后 a 应该会向下加速,而 b 在放手后的一段时间里应该会保持静止。下面啊,我们重新看一下刚才的实验,验证一下这个结果。注意观察小球是怎么运动的啊, 看到了没,在放手后的很长一段时间里, a 球是向下动的,但 b 球没动,和我们预测的结果啊,是相同的。题目做完了,我们来简单总结一下这类题目该怎么做。这类问题啊,让我们求物体受力突变瞬时的加速度。 这时啊,一定要记住,不管别的力怎么变,弹簧弹力是不会突变的。掌握了这一点,我们只需要两步就能算出加速度了。首先求出突变前弹簧的弹力,然后第二步呢,把这个弹力带入到突变后,计算出加速度。 怎么样,学会了没?来,咱们再拿一道题出来,看看你掌握了没有?来看题, 如图所示,轻绳与轻弹簧之间既有一致,两位 m 的小球,小球处于静止状态。来,这两个标上小球静止呢,说明他受力平衡。接着读题,此时轻弹簧处于水平状态,轻绳与竖直方向夹角为四十五度。在这最后呢,他把绳子剪断,问小球的加速度大小是多少? 剪断细线的话,那小球的受力肯定会发生突变。所以啊,这道题还是在问受力突变顺时小球的加速度。我们还是按上一题的思路, 先求出剪断前弹簧的弹力,再带入到剪断瞬间,计算加速度。先求弹簧弹力,对小球做受力,分析他受重力,绳的拉力以及弹簧的弹力,把这两个力平移过来,在这个直角三角形里,这个角是四十五度,所以这个重力和弹簧弹力是相等的,所以弹簧弹力等于 mg。 接下来把这根线去掉,来球剪断瞬间小球的加速度。这时候啊,小球受 mg 的重力以及一个向左的弹簧弹力,弹簧弹力不会突变。在这呢,还是 mg 写到这里来?所以呢,小球的合力也很容易算,等于根号二 mg。 最后呢,把这个合力带入到牛登天定律里面,那加速度就算出来了,是根号二 g。 怎么样,你做对了吗?好,总结一下, 求受力突变顺时的加速度,关键在于弹簧弹力不突变。根据这一点,咱们解这类题只需要两步,先求出突变前的弹簧弹力,再带入到突变瞬间求出加速度就行了。
1494洋葱学园赵老师 01:12
01:12 02:30
02:30 00:32查看AI文稿AI文稿
00:32查看AI文稿AI文稿英文比中文更难。切,就拿一个我字来说,男的用爷,女的用娘,皇上用朕,皇后用哀家,百姓用鄙人,老人用老夫,青年用小僧,和尚用贫僧,道士用贫道,粗人用咱,文人用小可豪放,可以用洒家 文曰可叫不才对上称,在下对下称,本座平民用草名。可是英文就一个 i。 那你英语还老不及格,英文中文我至少能看懂啊。哎呦我的妈哈哈哈。
1.3万洋葱学院李狗蛋
猜你喜欢
- 37.7万外滩碎嘴孙二娘








