九年级下册圆的基本元素教学板书

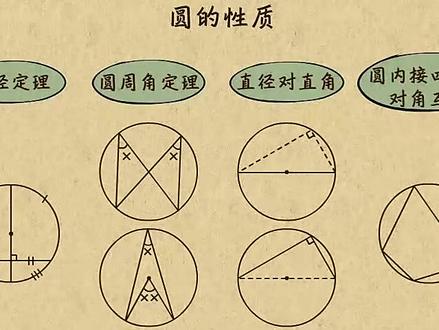
这个视频为师来带你复习一下圆的性质。要掌握这个内容，你们得先熟悉这四大定理，垂径定理、圆周角定理，直径对直角以及圆内皆似平行，对角互补。下面就分别来复习一下。 垂青殿里说的是这么回事，这是一条弦，如果或圆心做一条垂直于弦的直径，那直径就会平分弦，并且平分这两段弧 光说一下，你们可能没啥印象，我们再来看个例子。如图，一支元欧的半径是五弦， ab 的长度是八， op 垂直 ab 求 op 的长度。 现在 o p 垂直 a b。 由垂青定理可知， a p 等于 b， p 都等于四，现在 a p 是四， a o 是五，利用高估定理就能算出 o p 得三。 好了，题目都做完了，来小结一下，解决这题的关键是垂青定理，只要看到垂直，你们就要想到平分。下面再来说说圆周角定理。 这个店里有两层含义，一层含义是这样的，铜壶所对圆周角相等。还有一层含义是这样的，铜壶所对的圆周角等于圆心角的一半。 假如这个圆周角是三十度，那对应的圆心角就是六十度。好了，这个定理先说到这，再来说说直径对直角。这个定理也包含两层意思，如果 ab 是直径，那 ab 所对的圆周角就是九十度，这是第一层意思， 而第二层意思就是把第一层意思反过来，如果这个圆周角是九十度，那他所对的弦就是直径。总而言之，看到直径要想到直角，看到直角 也要想到直径。下面我们再通过两个例子来巩固一下。先看第一个，如图，一支 ab 是圆， o 的直径，角 d 等于四十度，则角 cab 的度数为， 观察这个图形，一只脚 d 是四十度，根据铜壶所对圆周角相等可知，角 b 也是四十度。知道这些怎么求角 cab 呢？对了， ab 是直径，所以角 acb 是直角，这样一来，角 cab 就能求啦，等于九十度，减角 b 得五十度。 好了，小结一下，这个题用到两个定理，一个是铜壶所对圆周角相等，还有一个是直径对直角。再来看第二题，如图，一只圆 o、 a、 b、 b、 c 是圆 o 的两条弦， a、 b、 e 等于六， b、 c 等于八，并且角 a、 b、 c 等于九十度， 则原欧的半径等于多少？下面就来分析一下。一只脚 abc 是九十度，你们会想到什么呢？ 所以啦，可以连接 ac， 由直角对直径可知， ac 一定会经过圆心 o 一支 ab 等于六， bc 等于八，用高固定力算一算， ac 就等于十， oa 和 oc 都是五。搞定好了，小结一下这个题本质上就是在考察直角对直径， 你们以后看到直径就要想到直角，看到直角也要想到直径。最后再来说说园内皆四边形对角互补。 这个定理说的是这么回事，如果这是圆的一个内接四边形，那么他的两组对角都互补，如果这是六十度，那他的对角就是一百二十度，如果这是一百一十度，那他的对角就是七十度。 怎么样，简单吧，只要看到圆的那些四边形，你们就要想到他的对角互补。好了，都说完了，最后来回顾一下对于圆的性质，你们要熟悉掌握这四大定理。 一、垂性定理，既垂直，弦的直径会平分弦。二、圆周角定理这个定理有两层含义，一层含义是铜壶所对圆周角三等。另一层含义是铜壶所对圆周角等于圆心角的一半。三、直径对直角这个定理也有两层含义， 一层含义是直径所对的圆周角是九十度。另一层含义是九十度的圆周角所对的弦是直径。四圆内接四边形对角互补记，这组对角的核是一百八十度，这组对角的核也是一百八十度。怎么样，都明白了吗？明白的话就速速去刷题吧！

上个视频介绍了和圆相关的基本概念，其中对圆的半径都相等这一废话式的结论做了新的定位，任意两条半径可以引出等腰三角形。等腰三角形有很多重要结论，这些结论在圆的世界里又能绽放出什么光芒呢？一起来学习一下吧！ 圆是轴对称图形，每一条直线所在的直线都是圆的对称轴，比如把圆这样对折，或者这样对折，相应的两部分都会重合。 在元欧上取两点 ab， 那三角形 oab 就是等腰三角形，也是轴对称图形，所以现在得到的整个图形就是轴对称图形。 对称轴是这样一条直线 l 把整个图也 l 对折一下，看，两边果然重合了。 l 被原所节的部分 d、 e 是圆的尺寸， l 被三角形 o a、 b 所结的部分 o、 c 则是三角形 o a、 b 底边上的膏。 说到短，要三角形底边上的高能明显到什么呢？答案是三线合一这个神奇的结论。根据三线合一， oc 平分 ab， 也就是 ac 等于 bc。 现在把眼光放到整个原理，刚才的结论就可以变成，若直径第一垂直于写 ab， 则直径第一就平分写 ab 其实有变身性。还可以知道，活 a、 d 等于壶 bd， 活 ae 等于壶 be， 因此直径第一还平分两条壶活 ab 和壶 adb。 把这些结论总结一下，就是 垂径定理，垂直于弦的直径平分弦，并且平分弦所对的两条弧。所谓垂径，就是垂直于弦的直径。看三线合一这一无比熟悉的结论，就这样在圆的世界里荣获今生了。 现在换个方向看，在原欧中，直径 ab 垂直弦 cd， 下面哪个结论是错的呢？ 答案选 b， acd 就是垂进定理。注意， b 虽然从图上看着很像，但这个图稍微变一下就能看出问题了。 在实际做题时，垂禁令里还有另一种样子，在于 o 中 o c 垂直 ab 根据垂禁令里有 ac 等于 bc。 说到这会有人疑惑了，这连个直 定都没用，哪来的垂经定理啊？所以这里的 oc 经过圆心 o， 他就起到了和直径同样的作用。 事实上， oc 还有自己的名字，他代表圆心到弦 ab 的距离，因此被称为弦心句，只要有弦心句，一样可以使用垂经定理。 现在你应该已经对垂经丁里无比熟悉了，那垂经丁里反过来说行不行呢？平分弦的直径是否一定垂直弦？ 答案选 b。 看下图，原欧的两条直径 ab cd 互相评分。换个说法，直径 cd 评分写 ab， 但他并不垂直于写 ab， 因此评分写的直径不一定垂直。写怎么样？是不是被这个出 惊呆了？因此要把垂经定理反过来说，得加一点限制条件，平分险的直径垂直于斜，并且平分斜所对的两条弧。哎，注意括号里的三个字，非直径。这就是垂经定理的推论。 垂进定理本质上就是三线合一，因此垂进定理的某些用法和三线合一是完全一样的。比如下面这个题，如图，三角形 ocd 为等腰三角形底边 cd 交于欧于 ab 两点。求证， ac 等于 bd。 这个图看上去结构简单，条件也清晰明了，想来不会是什么难题。要证明 aca 等于 bd， 相信有不少小伙伴有这样一种冲动，连接 oa ob， 证明三角形 oac 全等于三角形 op， 这种做法非常非常棒，但是还有更简单的做法，那是什么呢？ a 就是垂青定理，在这个处理， ab 是原物的斜。垂青定理呢，说的是垂直于弦的直径，平分这条斜，所以要用垂青定理，就得先有垂直于弦的直径。对于这道题来说，就是垂直于斜 ab 的直径， 但是在实际做题时，并不用真的做直径。还记得写信句吗？他起到和直径同样的作用，因此做写信句就可以了， 也就是做 oe。 垂直 ab 于 e。 根据垂进定理， ae 等于 be。 除此之外，还有什么结论呢？最大三角形 ocd 是等腰三角形 caec 和 e、 d 也相等，有了 a 等于 b， e， c， e 等于 d， e 两个数字一相减，就得到 a， c 等于 b、 d 了。 这种写法用到了垂经定理，为此做出了弦心区 oe 这一关键线段，凡是和弦有关的问题，都可以考虑做弦心区。求解。 再告诉大家一个小秘密，这个题的原型就是下面这个题，大家对比一下是不是非常像。其实刚刚这个题只是用圆 o 代替了 oa 等于 ob 而已，所以两题的结法也是如出一辙。 如此说来，垂心令里岂不就是三线合一的翻版，毫无新意了？ no， no， no！ 垂心令里在使用时是有其独到之处的，其中的关切就是闲心去。看完这个例子你就明白了。 如图， ab 是原物的直径， cd 是企业， ab 垂直 cd 与点一。若 ab 等于十， oe 等于三，求 cd 的长。 题目中出现了 ab 垂直 cd， 那根据垂经定理， ce 等于 d， e 等于二分之一 cd 要求 cd 的长，只要求出 ce 或 d e 就可以了， c e 或定义又怎么求呢？题目给了 o e 等于三，这就是闲心剧吗？ o e、 c e 和 o c 恰好组成的一个直角三角形，如果知道 o c 的长度，就可以求出 c e 了。 o c 就是半径。题目上说， a b 等于十，也就是十，径等于十，因此半径就是五，也就是 o c 等于五。那这样一来， c e 就等于四了，因此 c d 等于两倍， c e 等于八。一起来看一下解题过程。 在写这道题时，用到了直角三角形 o c e， 它的三条边都很独特， o c 是半径， o e 是弦心句， c e 是弦， c d 的一半，它被称为半弦长。 事实上，对于任一条非直径的斜半径，写新剧半弦长都可以组成直角三角形。这样的直角三角形就是解决与弦长有关的黄金三角形。 凡是设计到嫌长时，都可以考虑做出黄金三角形，利用勾股定理解决问题。说到这，水晶定理和 基本应用方法已经介绍完了，大家可以看图再回顾一下，相信很多小伙伴肯定还不过瘾，没有关系，下个视频将继续介绍垂经定理的高级应用，快来学习吧！

今天我们一起来学习或扶贡线三点做元先我们一起来看一个前进语录， 老师不小心将心爱的云行化妆镜打碎了，只留下如图所示的一块玻璃了。可是老师太喜欢这面镜子了，同学们，你们能帮老师破镜重圆吗？能，这么牛对不对？ 那么先问大家，原是什么把地面的距离等于面朝的所有点组成的图形哦， 这是一面圆形的镜子，要确定这面圆形的镜子，关键的就是要满足几个条件呢？两 就是我们刚才讲的定点，定点就是指的什么人心定常指的就是放屁。那如何来确定这面镜子的云心和棒剑呢？带着这个问题，我们今天一起来探究。 先复习回归一下现状的垂直平分线的性质定理及立定理。性质定理是 垂直平分线上的点到线段，两个个距离相等。