物理高一怎么画斜面受力分析图
三十秒教你从四个题变成送分题,咱们今天继续讲高中物理斜面含外力模型的模块。第三部分我们接着来分析。对于图四, f 相当于增大了重力沿斜面的分力,所以 f 增大镜摩擦力就等于 f 加 m g sin x, 增大支持力不变。 咱们再来看图五, f 相当于增大了重力垂直斜面的分力,则 f 增大支持力等于 f 加 mg cosine x 增大镜摩擦力不变。 接着来看图六,将 f 分 解为沿斜面向上的分力。 f cosine 二法受力分析就如图九所示。那么我们来讨论。第一个,当 f cosine 阿尔法等于 mg cosine, 它使鞋面对物块是没有摩擦力的。第二点,若 f cosine 阿尔法等于 mg cosine, 它使此时物体会脱离鞋面,鞋面对物块无摩擦。 第三,入斜面对物块有摩擦力的作用时,那么我们还是要继续讨论。当 f cos 向量大于 mg cos, 它使摩擦力沿斜面向下, f 增大时,则有支持力。 f n 就 等于 mg cos, 它减, f cos 二法是减小的。近摩擦力等于 f cos 向量减, mg cos, 它是增大的。 第二个情况, f cosine r 小 于 mg cosine, 它是摩擦力沿斜面向上, 当 f 增大时,则有支持力。 f n 等于 mg cosine, 它减 f cosine r 法是减小的,其摩擦力等于 mg cosine r, 它减 f cosine r 法是减小的。 当 f 继续增大到 f, 除以 alpha 等于 m g sin c 时,摩擦力开始反向,与我们圈一分析的是相同的,整个过程中 f 竟先减小后增大, 所以我们来总结一下此类问题。我们需要充分考虑重力的两个分力,计算支持力时要注意垂直斜面方向的力的大小关系。记 算近摩擦力时,要注意沿斜面方向的力的大小关系,必要的时候要进行分类讨论。好了,那今天就讲到这里了,大家再见。
粉丝166获赞2000
相关视频
 01:56查看AI文稿AI文稿
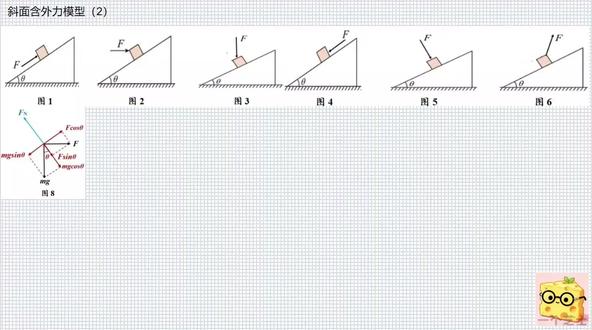
01:56查看AI文稿AI文稿今天我们讲斜面和外力模型的模块二来看,图二中 f 分 解为两个分力, f cosineit 和 f cosineit。 如图八所示,若 f cosineit 等于 mg cosineit 时,此时斜面就对物体无摩擦力。 第二点,若 f cosineit 大 于 mg sineit 时,此时斜面对物体镜摩擦力方向沿斜面向下,镜摩擦力的大小就等于 f cosineit 减 mg sineit。 斜面对物块支持力 fn 等于 mg cosineit 加 f cosineit, 此时 f 增大时,支持力增大。镜摩擦力增大要使物体向上滑动,那么 f 有 最小值。 若 f cosinect 小 于 mg sinect 时,那么斜面对物体镜摩擦力方向就沿斜面向上,镜摩擦力的大小就为 mg sinect 减 f cosinect。 f 增大则由镜摩擦力减小到 f 增大到 f cosinect 等于 mg sinect 时,摩擦力开始反向。 当 f 继续增大时, f cosineit 大 于 mg cosineit 时呢?就与我们分析的第二种情况相同,整个过程经摩擦力先减小后增大。 我们再来分析图三。在图三中, f 相当于增大了物块的重力,当 f 增大时,有支持力就等于括号 mg 加 f 乘 cosineit, 此时镜摩擦力就等于括号 m g 加 f size, 它也是增大的。好啦,那今天就讲到这里了,我们下次再见。
42一个芝士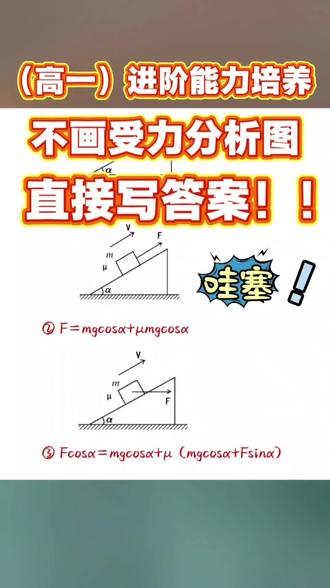 04:51查看AI文稿AI文稿
04:51查看AI文稿AI文稿同学们好,我是梁老师,这个视频梁老师教大家一个非常实用的好用的技巧, 不用画受力分析图就可以快速写出答案。我们先来看例子,上面三个斜面模型是共点力平衡常考的题型,如果按照常规法受力分析可能要两到三分钟,但梁老师可以直接写答案,只需二三十秒。 下面梁老师将这种方法教给大家,如果学会了,我们就可以不需要每道题都去做受力分析图,可以节省大量的时间和精力,也可以让我们对历学模型的分析,解析思路的形成,解析速度的提升有一个质的飞跃。 我们先来看第一个基础题型,一个质量为 m 的 物块静止在鞋面上,求物块受到的支持力和摩擦力。这个模型在上个视频老师用三种方法进行受力分析,摩擦力大小等于重力在鞋面方向上的分力,除以 x, 知识力大小等于重力在垂直斜面方向上的分力 g y, 所以 答案是 f 等于 g x 等于 mg sin r 法, n 等于 mg cosine r 法。 接着看变式,一,物块在沿斜面方向 f 的 作用下,沿着斜面匀速上升,已知物块与斜面的摩擦系数为 m, 求 f 大 小。 像这些斜面蹄形,我们一般先分析斜面方向上的受力平衡,沿着斜面向上的是拉力 f, 沿着斜面向下的是重力。分离阻力和摩擦力 f, 所以力的大小关系为, f 等于 g s 加小 f。 又因为滑动摩擦力等于 mu n, n 等于 g y, 所以 答案是 f 等于 m g sine alpha 加 mu m g cosine alpha。 同学们能够听得懂老师分析的思路吗?如果可以,请在评论区打个能字。如果听不懂,老师现在把这个受力分析图画出来,同学们可以对照这个分析图,再去听一下刚刚老师分析的思路, 直到自己可以不看受力分析图,直接熟练的写出答案为止。我们接着加大题目的难度来看便是。三、 此时拉力 f 是 水平向右的。相对上一题,这一道题 f 需要分解为沿着斜面方向的 f x 和垂直斜面方向的 f y。 其他的思路是一样的, f s 等于 g x 加小 f, f 等于缪 n, n 等于 g y 加 f y。 所以 答案是 f cosine r 法等于 m g sine r 法加缪。括号 m g cosine r 法加 f sine r 法。 同学们听明白了吗?这张是受力分析图,同学们可以自己对照一下。最后我们来看水云方向题型下面这道例题, 物块在 f 的 作用上沿着水平方向匀速向右运动,已知 f 与水平方向的夹角为 c 塔,地面摩擦系数为 mu, 求 f 大 小。 这一道题按照正角分解, f 给分解为水平方向的分力 f x 和数值方向的分力 f y。 又因为物块受力平衡,所以在水平方向 f s 等于小 f, f 等于 mu n, 数值方向 n 等于 m g 减 f y, 所以 答案是 f cosine 等于 mu, 括号后 m g 减, f sine 减。 这个是受力分析图,同学们也可以参照一下。同理,如果 f 是 斜向下拉动物块,此时 f cosine 等于 mu, 过后 m g 加 f sine sine sine。 在高中历学,鞋面模型和水面模型是出现的最多的模型,所以我们记住一些参考的模型,把受力分析图刻在脑子里,在平时的练习题直接写出答案,可以让我们节省大量的时间和精力,也为我们后面的深入学习打下基础。 很多同学一开始可能会不适应,但只要勤加练习,相信你们很快就可以掌握技巧。可能有些同学会有顾虑,这不是死记硬背吗?恰恰相反,我们记住一些参考的模型,以点带面就可以发散思维。 好了,我是梁老师,关注我,我会分享更多的方法技巧,我们下个视频见!拜拜!
29物理培优微课堂 05:26查看AI文稿AI文稿
05:26查看AI文稿AI文稿好,那是再看鞋面上的受力分解器,鞋面上我们单个物体啊,像这种静止的啊,静止的,比如说像这个物块搁这鞋面上,静止受力,受重力支持力,那么一定这个物块有一个向下滑的趋势,所以鞋面给它的摩擦力向上的, 那如果这个物块啊,这个鞋面光滑,鞋面光滑,你想这个物块放在这,如果没有外力 f, 如果没有外力 f 的 话,那它受重力支持力,那么这个鞋面呢,这个物块呢,一定沿鞋面向下滑,向下滑,那因为有这个 f 的 存在, 对这个物块可以搁这平衡,那此时没有摩擦力,为什么呢?因为鞋面光滑,不受摩擦啊。 下面,那如果我们各接触面均光滑,此时这个球呢,放在鞋面上,那么有一个挡板挡住了它,那对这个球进球的分析,重力弹力, 我们先重力,弹力,那因为你各个面都光滑,肯定没有摩擦力,所以只有重力和弹力,我们看重力,看一下弹力,那么支持力是弹力,那么垂直于这个接触面,那么这个垂直接触面指向输入压的地方,所以 f n 一, f n l, 那么这个也是这个,只是这这个面呢,这个挡板呢,它的方向改变了重力,那么这个 f 二 n 二,那么垂直挡板向上,那么这个 f f n 一 仍然是不变的垂直接触面啊。 好,那这个物块呢,我们可以看为置点,现在静止在斜面上,那么分析这个斜面的受力 啊,那刚才呢,我们是分析的这个物块,我们现在要分析斜面。好,分斜面的话,分析斜面,你可以先分析物块啊,分析物块,那根据力是相互的,那这个物块受什么力呢?受重力, 然后呢这个斜面给它一个支持力 f n, 那还会受到什么啊?还会受到鞋面给它向上的一个摩擦力,因为这个物块有向下向下滑的趋势,那么所以鞋面给它的进摩擦力是向上的 f。 好, 那我们分析出鞋面给物块的力,这是我们在分析这个鞋面受力,鞋面受什么力呢?受重力, 说中理,那么地面会给他一个向上的支持力,那因为你这个鞋面给物块的支持力是垂直鞋面向上,那反过来,你物块对鞋面的一个压力应该是垂直鞋面 向下,还有的你斜面对物块的摩擦力是沿斜面向上,那么物块就斜面的摩擦力就沿斜面向下了啊,所以它应该是这四个力,是不是四个力,那么这四个力呢?平衡是吧?能平衡,所以这个可以改成静止。 好,那么如果这个物体是运动的,运动的,沿着斜面运动,并且斜面不光滑,那么肯定受重力, 重力沿斜面向下,那么此时的摩擦力呢?是滑动摩擦力沿斜面向上的,因为跟相对的方向相反, 那么这个鞋面也不光滑,它的沿鞋面向上运动,沿鞋面向上运动,肯定正的支持力有,那么摩擦力也有摩擦力呢?跟它运动跟它的相对的方向相反,因为它这个物块相对于鞋面在向上走,所以摩擦力向下的鞋面向下啊。 好,那么再看传送带,传送带的情况,那如果是水平传送带,这个物块啊,跟传送带一起匀速向右运动,那么此时这个物块跟这个传送带啊,没有相对运动, 那么他这个物块只受两个力,重力跟支持力啊,那么第二种情况就是鞋面上的传丝带,但是这个物块啊,跟这个传丝带一起沿着鞋面向上匀速运动, 那么此时对物块受力分析,他一定受重力,传丝带给他一个支持力,那么此时这个物块他要能够跟传丝带一起沿着鞋面向上运动,此时的受力平衡,那么他一定会受到一个沿鞋面向上的摩擦力, 那么只有沿斜面向上,此时这个物块呢,才能够平衡,才能够匀速向上运动。那么第二个, 如果这个物块它随着传送带一起沿着斜面向下匀速运动,那么直接受力分析,向下匀速运动,因为首先它处于平衡状态,重力 啊,这个鞋面可在支持力,那你现在匀速向下移动,那这两个力很明显不平衡,那么它还在摩擦力内,一定是沿鞋面向上的, 一定沿鞋面向上,此时这个物块呢,才能够保持平衡,才能够匀速运动啊,匀速运动,所以摩擦力也向上。 最近发现啊,这里这个传送带只要是匀速向上和或者是匀速向下,这个物块在传送带上,它的摩擦力呢,一定是沿斜面向上的,沿着传送带向上的,好,那这是斜面上的。
13初高中化学吕老师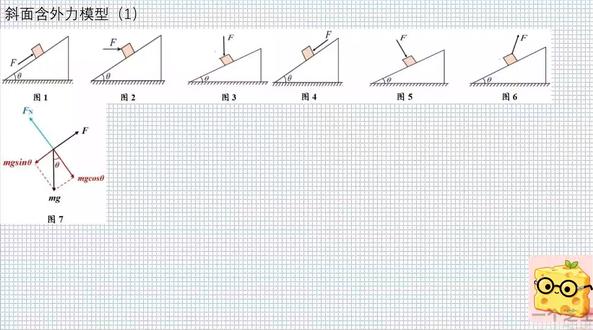 03:03查看AI文稿AI文稿
03:03查看AI文稿AI文稿三十秒教你从死壳体变成松松体!今天讲斜面上物体受外力的静力学分析模型, 这部分内容是固定斜面加静止物体受不同方向外力的静力学分析模型。我们的核心就是通过分解重力,比较外力与重力分力的关系来判断斜面对物体的支持力和静摩擦力的大小方向的变化。 所以我们从模型核心逻辑和图一的具体分析来两方面去梳理。首先大家要了解模型核心,前提斜面固定 物体始终静止。将物体的重力 mg 分 解为沿斜面向下的分离 mg cosineit 和垂直斜面向下的分离 mg cosineitit 为斜面的倾角。 斜面对物体的作用力包括垂直斜面向上的支持力 fn 和沿斜面的镜摩擦力。 镜摩擦力的方向大小由外力 f 与 mg sin 它的大小关系来决定。那接下来我们针对图一的场景详细来分析外力 f 沿斜面向上。 图一中,外力 f 沿斜面向上,所以要对比 f 与 mg sin 它的大小,分三种情况判断近摩擦力,当 f 等于 mg sin 时, 沿斜面方向外力 f 与重力分离 mg sin, 它大小相等,方向相反,合理为零。因此斜面对物体是没有近摩擦力的。 种情况,当 f 大 于 m g sin sin 时,斜面方向 f 的 大小 大于 m g sin sin, 物体有沿斜面向上的滑动的趋势,因此镜摩擦力方向沿斜面向下,大小为 f 等于 f 减 m g sin sin 越大,镜摩擦力越大。当镜摩擦力超过最大镜摩擦力时,物体开始沿斜面向上滑动。再来看第三种情况,当 f 小 于 mg sin x 时, 斜面方向 mg sin x 的 大小大于 f, 物体有沿斜面向下滑动的趋势,因此镜摩擦力方向沿斜面向下滑动的趋势。因此,镜摩擦力方向沿斜面向下滑动的趋势。因此,镜摩擦力方向为 f 等于 mg sin x, 它减 f。 当 f 增大时,摩擦力减小。当 f 增大到 f 等于 mg 上 in c 时,静摩擦力为零。 f 继续增大且大于 mg 上 in c 时,静摩擦力反向沿斜面向下, 且大小随 f 的 增大而增大。整个过程中静摩擦力因此先减小后增大。好了,那我们今天就讲到这里了,我们下次再见了,我是一个知识。
27一个芝士 28:59查看AI文稿AI文稿
28:59查看AI文稿AI文稿鞋面模型是我们期末和高考啊都是非常重要的考点,他除了会对鞋面模型进行直接考察以外,后面要学习的连接体模型、传送带模型和板块模型。当你把这些模型啊给他放到鞋面上的时候,他又会对鞋面模型的相关知识呢进行相应的考察。 那今天呢,我们就把鞋面模型的相关知识呢,给大家做一个详细的讲解。先看例题, 如图所示,一、物体正沿静止的斜面匀速下滑啊,就是处于平衡状态,核外力为零,像一个数值向下的力, f 作用在 f 上啊,作用在物体上,则问物体是否能够啊匀速下滑以及斜面啊受到地面的摩擦力是怎样的 啊?我们先对物体啊进行受力分析啊,分析它就是受力情况,向下受到重力 mg, 还有就是鞋面的支持力 f n 以及鞋面在它一个摩擦力啊,是不是就受到这三个力,在这三个力的作用下匀速下滑?我们先把重力啊给它分解一下,重力按照作用效果来分解,第一个呢,它就是沿鞋面下滑的下滑分离,另外一个呢,是垂直于鞋面产生的一个正压力啊, 假如这个轻角斜面的轻角是 theta, 所以 它重力的下半分力,我们要牢牢记住,就是 mg sin theta 啊,那它对斜面的正压力呢,就是 mg cosine theta 啊,这个 f 是 它滑动摩擦力啊,滑动摩擦力我们知道等于个 mu fn, 而 fn 呢,就会等于个 mg cosine theta, 所以 这个式它就变成了 mu mg cosine theta 啊,既然它能够匀速下滑,说明重力的下滑分离 m g sin sine theta 就 等于它向上的一个滑动摩擦力啊,就 mu m g cosine theta 啊, mu m g cosine theta, 那 这个式子啊,还可以给它变形一下啊,就是 mu m g 约掉 cosine theta 挪过来,所以它就变成了 mu, 是 不是等于一个弹定的 theta 啊?也就是物体在鞋面上,它的运动状态由谁决定呢?就由这个命弹性随大来决定的啊,和物体的这个质量是没有关系的。好,我们看一下啊,那再给他施加一个数值向下的力 f 啊,数值向下力,我们知道重力是不是也是数值向下的, 所以你加一个数值向那里,是不是相当于给这个物体他的重力增加了呀?你增加了物体的重力,这个你看没施加重力之前,他们两个是不是相等的呀?你施加重力,这 mg 就 变大了,这边 mg 是 不是同样变大了?但是这 mg 是 不是可以约掉的呀? 因此啊,他的重力是并不会影响他在鞋面上运动情况,因此你施加一个外力, f 呢,他依然能够啊,仍然能够匀速下滑,所以 a 是 正确的,那 b 就 错了。 好,再看一下 c 和 d 鞋面受到地面的摩擦力是怎样的?那既然是鞋面受到,所以我们对鞋面是不是要进行受力分析啊?好,鞋面,假如鞋面的质量啊,是大 m, 那 因此呢,向下的重力啊,就是大 m 计啊,那他是不是还有支持力啊?支持力我们用 f n 来进行表示。 好,还有就是斜面向下滑的时候,他给他这个物块沿斜面向下滑的时候,他给斜面是不是有一个向下的摩擦力啊,这就用 f 撇来表示,要知道 f 撇和 f 是 不是作用力,反作用力他们等大反向啊?那另外呢,还有就是物体啊和物块是不是对这个, 对这个鞋面是不是产生一个压力啊?这个压力啊和这个 f n 啊,这个 f n 和 f n 点是不是也是重力反重力啊?它们等大反向啊? 先看我们不施加这个外力 f 之前啊,这个物体是不是匀速下滑,那它向上这个 f n 和 f 这两个力的合力是不是一定与重力是不是等大反向? 因此你不施加外力的时候啊,你不施加外力的时候,那这 f 撇二是等于 f 呃, f 撇二是等于 f f n 撇二是等于 f n, 所以 它们两个的合力啊,在你不施加这个外力 f 的 时候,它们两个合力是不是也是数值向下的 啊?竖向下啊,那我们知道,刚才已经知道了, f 撇是等于 f, f n 撇是等于 f n 的, 所以 f 撇是不是也会有啊?它等一个是不是 m f n 撇啊?啊?因为 f 啊,这个滑动它里就等于个 m f n 啊? 啊,那 f n 等于 f n 撇, f 撇又等于 f, 所以 是不是就有这个式子啊? 啊?看,当我们说施加一个数值向下的力 f 的 时候,是不是就相当于这个物体它的质量重力增加了呀?当重力增加,是不是会影响它的正压力的增加 啊?正压力是不是 f n 撇增加, f n 撇增加,那 f 撇是 f n 撇,你看是不是缪倍啊?所以它增加了多少,它是不是就以缪倍是不是也是增加的呀? 也就是说是成倍增加啊?成倍增加的,那你 f 撇和 fn 撇本身合力啊,在不施加外力的时候,它合力是不是数值向下的?那你现在 fn 增大了, fn 撇呢?成倍增加,所以它们的合力是不是还是数值向下的? 那既然这个小物块对斜面的合力还是沿着竖直向下的,那因此斜面是不是就没有在水平方向上移动的一个曲式啊?因此他在水平上,地面对他的所外,这个摩擦力是不是等于零啊? 那地面摩擦力等于零,所以他就不会向左,是不是也不会向右,所以 c d 都错了啊,那这就是这个斜面模型它的点力,那接下来呢,我们就把这个斜面模型的相关知识啊,都给大家进行一个系统的梳理 啊。先看第一个,就物体在光滑鞋面上滑动啊,如如图所示啊,物体在光滑的这个鞋面顶端啊,有顶端啊,像这个下下滑的过程当中,我们对它进行受力分析啊,还是竖直向下的重力以及支持力,是不是只受到这两个力啊?那没有了,因为他 光滑了,所以没有摩擦力,只测这两力。我们把重力啊也给它分解一下,那重力有两个作用效果,第一个呢,是不是就是沿沿斜面方向啊?沿斜面方向。另外一个呢?这个重力是不是垂直斜面方向产生的这个正压力啊?假如说轻点 c 叉的话,那它的下滑分力是不是 m g sin theta, 然后它正压力就是 mg 有 cosine theta, 好 在沿鞋面方向啊,因为不受到摩擦力,是不是它只受到这个重力的下滑分力啊?那因此它在鞋面产生的加速度 a 啊,是不是它这个核外力除以质量就可以了,就等于 g 乘上一个 sin theta 啊,这就是在光滑鞋面上的时候,你把物体放在鞋面上啊,它能够产生的加速度就等于 g 乘上一个 sin theta 啊。关于鞋面,大家要记得就是他的下拉分离和垂直鞋面方向的压力,以及在光滑鞋面产生加速度,是 g c d 都要给他记下来。好,我们看一下关于在光滑鞋面上他常用的结论都有哪些啊?第一个呢,就是等高光滑鞋面啊,看右边这个图, 这个高呢,都是 h 啊,都是 h 是 等高的,那他的倾角不同,也就是这个斜坡啊,他的这个倾斜程度啊不同, 那在一二三啊,他从鞋面顶端啊,从鞋面顶端啊,沿着这个光滑的鞋面由静止开始下滑,他们的时间呢?这里要知道是 t 一 大于 t 二大于 t 三,那这个也比较容易求出来啊,也比较容易证明。你看从鞋面顶端滑到底端 啊,那这时候我们知道它的谓一,知道谓一的话, x 由静止开始下滑,所以谓一共是 x 是 不等于二分之一 a 一 t 的 平方, 那你这个式子一变形啊, t 是 不是等于个根号下 a 分 之二 x 啊?啊,我们观察在这个三十度的时候,三十度的时候,它下滑的时候加速度,我们是不是都知道了,是 g 是 不是乘上一个 c, c 大, 是不是它下滑的时候加速度啊? 你看 c c 大, 这时候 c 大 是不是比较小啊? c 大 小加速小啊,它的位移呢?比较大,你看位移大,加速小,所以你求出来这个时间是不是就比较 上面大下边小?所以你求出来这个位置是不是比较大的呀?因此我们就可以依次可以求出来 t 一 是大于 t 二啊,再大于 t 三啊,这就可以证明出来啊,他的这个越倾斜啊,他滑下来所需要的时间越长。 另外呢,我们也可以用上一节课时讲的等式圆模型来进行解决,你看这是不是最高点,我们就以它为最高点,然后做圆,做圆的话,最高点向下,竖直向下,圆心是不是肯定在这个竖直向下的一个直径上, 然后以二这条这条啊,这个这个路径啊为弦啊,那他的垂直平面是不是肯定过圆心啊?好,我们画圆画圆啊,这时候不用画画全啊,只需要过到这就可以了, 好,画圆。你看这时候不就是我们等式样模型吗?从最高点沿着光滑斜面由静止开始下滑,他到达圆上各点所用的时间是不都是相同的 啊?所以时间都相同的。那到达这个时候啊,你看是不是他想要到达底端,是不是他还要移移动一段时间?所以 t 一 是不是更长,然后到 这个他是不是到达原上?对于这个三,你看是不是他还没到达原上,所以他的时间是不是最短啊?所以我们可以得出 t 大 于 t 二 t 的 啊,这是关于等高光滑斜面,这个比较容易理解,也比较容易证明。 下面再看一个关于这个同底光滑斜面啊,也是从最高处然后滑到这个底端,它所用的时间。这刚才我们已经得出 t 是 不是等于根号下 a 分 之二 x。 好, 我们只需要求出它的 x 和它的加速,是不是就知道它的时间了?好,假如说这个角度啊,为 c 档,你看它的底, 它的 d 是 不是就是二,是不是就是 d 啊?所以这个位移从这划到这,它位移是不是也可以表示出来?那 x 呢,是不是就等于个 d 比上一个 cosine sine? 因为 cosine sine 是 等于个 d 比上 x, 所以 x 呢,就等于个 d 比上一个 cosine sine, 这是它的位移,那加速度呢? 你的轻角是 c 大 啊,它向下滑的时候,加速度是不是 g 渗 c 大? 好,那它加速度 a 就 等于一个 g 乘以一个渗 c 大 啊,你给代入到这个式子当中啊。代入到式子当中,那我们给它写到这儿。 好,下边啊,是 a 啊, a 分 之二 x 嘛,所以就是计算器的上面是二 x, 二,先写出来。 x 呢,是不是等于个 d 比 cosine 啊? d 给它写在上, cosine 是 不是可以写到下边? 现在上边下边都同时乘上一个二啊?二,那所以上面就变成四 d 了。 好,你看 g 二倍的 sin, sin cos 啊,是不是变成了 sin 二 sin 啊?观察这个式子,观察这个式子,你看,当 sin 等于四十五度的时候, sin 九十度,是不是等于一啊?那下面有最大值,所以 t 是 不是有最小值啊?那因此我们可以知道,当 sin 等于四十五度时,这个时间 t 啊,是不是有最小值啊? 啊?这个最小值,那就是 c 大 等于 c 二, c 大 等于一了,所以是不是等于根号下积分之四 d 啊? 积分四 d, 这个我们要给它记下来。对于同底光滑鞋面啊,同底光滑鞋面,那这时候啊,他的这个这个鞋面啊,他的倾角是四十五度的时候啊,他的下滑时间是最短的啊,最短时间呢,就等于根号下积分之四 d 啊,这是关于光滑鞋面,那我们看一下,在粗糙鞋面上滑动啊,假如说这个物体沿粗糙鞋面向下滑的话 啊,那还是对物体进行受力分析,受重力,弹力,还有这个摩擦力,那对重力呢?还是给他分解分解?刚才我们就知道重力的下滑分离是不是 m g 渗水道,然后对鞋面的正压力 啊,是不是 mg cosine theta 啊, mg cosine theta 啊,这个摩擦力啊,就是滑动摩擦力呢,滑动嘛,滑动摩擦力,所以就是 mu fn, 是 不是要等一个 mu 啊? mg 是 不是 cosine theta? 好,我们来看。分析完了之后啊,就看物体他在鞋面上到底做怎么样的运动,也是他的运动形式,就取决于他的摩擦因素和鞋面倾角啊, c 叉之间的一个正切值啊, c 叉啊,正切值,弹性 c 叉之间的关系就取决于 mu 和弹性 c 叉, 那不行,我们来看,你看,当 miu 小 于 tan theta 的 时候,我们把这个式子给它进行一个变形啊,它就变成了 miu m g cosine theta 小 于 m g sin theta, 那 你把这个式子等式两边同时除以 m g 把 cosine theta 挪过来,是不是就是 miu 小 于 tan theta, 所以 miu 小 于 tan theta 可以 变形成这样? 好,这是啥?你看这个是不是他的摩擦力啊,这个是不是他下滑分力啊,也就是物体在鞋面上,他的向下的滑动摩擦力是大于啊,大于他向上的一个,这个向下的下滑分力啊,是大于他的一个滑动摩擦力的, 那因此物体运动情况是不是就决定了,你把这个物体放到这个鞋面上的时候,假如你以无出速度给他放到这鞋面上,因为他向下滑的下滑分力,你看下滑分力是不是比较大, 然后是不是比它的最大筋膜面积还大,所以它一定是不是会向下加速啊?啊?向下加速,这不就知道它运动情况了吗?好看。第二个,这个是不是也可以给它变形啊?那就变成了 mu m g q c 的是不等于 mu g c 的 好,这时候我们知道它的下滑分力啊,下滑分力 m g c c 啊,是不是等于它的滑动摩擦力啊?如果说你把这个物体啊,给它一个出速度,给它一个出速度,它是不是就以这个出速度匀速下滑? 因为它向下的下滑分力是等于它沿斜面向上的,是不是滑动摩擦力啊?那它相等的话,你给它一个出速,它是不是就以这个出速度,是不是匀速运动啊?如果说你给这个物体啊无出速度给它放到这个斜面上,它是不是还是能够静止在这 啊?还是能够静止在这?因为我们知道啊,它的最大的摩擦力是不是要比它的滑动摩擦力稍微,是不是要大那么一点点啊?那大那一点点,那是不是说明向下的下滑分力是不是小于它的最大的摩擦力啊?啊?所以你要是无出速度放到这个斜面上的时候,它是不是会静止在这?好,然后再往下看, 那当 miu 大 于它的斜率是不是大于 miu 斜率,斜率 那是啥意思?是不是物体的下滑分力啊?是不是小于他的滑动摩擦力啊?那如果说你把这个物体静止,就是无出速度放到这个鞋面上,他是不是就在这静止啊? 如果说你给他一个向下的速度啊,让他向下运动,但由于他的滑动摩擦力向上啊,并且他大于他向下的一个这个重力的下滑分力, 所以是不是他是加速度,是不是向上的,是不是他也是减速减速,减速减减到零之后是不是还是静止在鞋面上?这就是物体在粗糙鞋面上滑动的时候啊,主要他的运动形式啊,就是由这个 mu 和 tanneasy 决定的啊。那这三种情况,大家如果是分析好之后,给他记下来 啊,给他记下来。好,那接下来呢,我们看几个例题,如图所示,数值墙上 a 点和地面上 m 点啊, a 点和 m 点呢?他们到墙角的距离相等,假设都是 d 啊,都是 d, 那 这个角度是不是就是四十五度了? 好, b 呢,在 a 点的正上方, c 点呢,在 m 点的正上方,并且呢, c 与 a 等高,那所以这个 c 点 他的高度是不是也是低啊?啊,现在有三个完全相同的小球, abc 啊, c 球呢,从这个 c 点做自由落体运动, a 球呢,从 a 沿着这个光滑的 am 啊,落到这个底端,那 b 呢?他也是啊, b 球从这个 b 沿着光滑这个杆啊,然后到达 m 点 啊,它们的时间分别是 t a, t b, t c 啊,让比较它们之间的一个时间关系啊,我们先看 t c 啊,因为做自由论题运动,它的时间是比较容易算的,我们都知道做自由论题运动,它的时间 t 是 不是等于根号下几分之二 h 啊?那它的高度是 d, 所以 就变成了几分之二 d 啊, t c 就 求出来了。 然后你看这个 t a 啊,这是不是四十五度,相当于它和 b 是 不是就是同底啊?是不是同底光滑斜面?那同底光滑斜面,当 c 它等于四十五度的时候,是不是它有最小值啊?啊,它有最小值,所以 t b 下滑的时间 是不肯定大于 t a 啊,因为 t a 这个尖角是四十五度,它下滑时间是最短的呀。好,那 t a 等于多少呢? 当 c 加等于四十五度的时候,刚才是不是已经计算出来了,是不是等于个积分之四 d 啊?积分之四 d, 那 积分之四 d 呢,它就等于根号二,是不是 tc 是 不是也大于 tc 啊? 好,那根据这关系是不是就可以去看选项了? a 说 t 大 于 tc, 你 看 tc, 它等于根号二倍的 tc, 所以 它肯定大于 tc 啊, 所以 a 正确。那 t a 啊,这等于 t c 是 错的,然后 t a 等于 t b 也是错的,因为 t a 是 小 a t b 的, 然后是不是应该是 t a 是 不是等于根二 t c 啊,所以它是错的。这个题答案啊,选择的是 a 选项啊。我们再看第二题, 如图所示,倾角为 c 的 的粗糙斜面上啊,这个大 m 啊,上有一个物块小 m, 物体不受其拉力,斜面足够长,且始终啊,是静止在水平地面上 雾化的。鞋面间的摩擦因素是 mill 滑动摩擦力啊,等于它的一个最大的摩擦力。先让物体从鞋面底端以出速度冲上鞋面,然后物体到达最高点啊,又滑到鞋面底端。 好,我们来分析一下,先看这个 a 选项啊,你看他都冲上顶端,冲上这个最高点之后, 它又滑下来了,滑下来说明在上面是不是搁不住啊?那搁不住说明它的重力的下半边 m g c c 大, 是不是大于啊?它的沿斜面向上的这个滑动摩擦力啊,就是 m g m g c c 啊,小于 m g m g c c 大, 那你把这个式子一变形啊, m g m g 约掉,然后这个 c c 大 挪过来,那不就是 m g 小 于什么弹性 c d, 所以这个 a 是 不是错了呀? a 就 错了?好,我们再看看这个 b c d 选项啊,用物体沿着斜面冲上,冲上去的时候,我们对物体进行受力分析,物体受重力, mg 啊,啊,还有支持力啊,上上支持力 f n 啊,那这时候啊,我们把这个向上的时候,他是不是向上运动,他的摩擦力是不是向下的啊?这是把重力啊,给他分解沿这个方向啊,还有就是就是这个垂直斜面方向啊,那这时候既然向上运动的时候,向上运动的时候啊,他的荷外力 相应的时候和零应该等于多少?是不是 f 啊? f 是 不是等于一个?呃,重力的下滑分离加上一个这个滑动摩擦力啊?那重力的下滑分离就是 mg 有 散携带,然后加滑动摩擦力呢?就是 miu mg 有 cosine 啊,它是不是等于个 m a 上去的时候是不是它的一个加速度啊? 啊,那这时候是不是可以求出 a 上啊,上去的时候加速呢?是不是等于一个 gson theta 啊?加上一个就是 mu g cosine theta 上镜头加速度,那如果说它向下滑的时候呢?那向下滑的时候对物体进行受力分析,重力啊,重力,那这时候支持力,摩擦力是不是就得向上了?那对重力进行分解啊?重力进行分解, 好,那这时候向下的力啊,向下的时候它的合力是不是向下的?是不是重力的下半分力啊? m g sin sin theta, 然后这滑动滑动摩擦力是不是向上啊?所以就是减去 mu m g cosine theta, 是 不是等于个 m a 下来时候它的加速度?那 a 下来时候加速呢?就等于个 g sin theta, 是 不是减去 mu g cosine theta? 好,现在我们已经分析清楚了,上去的时候加速度是不是比较大一些?下来的时候它的加速度是比较小一些? 好,你看上去的过程从这到达最高点啊,从这到达最高点,那它到达最高点,整个的一个过程最终速度是不是变成零了?而且它加速度是不是等于一个 g 整数加上 minus, 那 你逆向思维是不是可以把它看成从最高点?从最高点是不是沿斜面下滑啊? 那他的加速呢?是不是为 a 一 啊?然后他向下滑啊?他向下滑的时候是不是也是初速为零啊?他加速多少?是不是啊?这个是 a 上,是不就是 a 下 拿一下啊?那你看这个第一个阶段啊,我们逆过来看,他是从上滑到底端啊,他的加速度是上去的时候加速度,那这个是下来的时候加速度,那上去的时候加速是不是比较大?相同的位宜,当你的加速度比较大的时候,你的时间呢,就会比较少啊,因为 都是初速为零,所以 x 等于个二分之一 a 是 不是 t 的 平方那位置相同?你的加速大,时间是不是就比较短啊?那因此物体上滑的时间是不是比下滑的时间要短啊?要短, 所以这个 b 是 错的。再看 c 选项,物体经过同一位置,速率啊,速率是上滑的时候大还是下滑的时候大?你看同一个位置啊,那不就是相当于还是对于上去的过程,那采用逆向思维来看,他是不是从零开始往到这个位置啊?就假如说在这个位置啊,同一位置 啊,打这个位置,那他是做什么呀?是不是他是以初速度为零,加速度为 a 上,是不是往这个方向加速啊?而而你下滑的过程当中啊,下滑的过程当中是以加速为零,他是加速,是不是 a 下 啊,是不是到达这个位置,那他的速度那末速度 v 是 不是等于个 a 乘上一个 t 啊? a 乘上一个 t 啊,或者说我们又不用这个,用我们这个负平方 v 方是不是等于个二 a x, 你看位移是相同的,如果说你的加速度大,那你的速度是不是比较大,那哪个加速大?是不是上去的 a 上是比较大,所以他滑到啊,上去的时候,滑到同一个位置时候,他的速率啊, 要大一些,要大一些。好,然后再看 d 选项,斜面所处地面的摩擦力啊,在物块上滑时比在下滑还大, 那还是看加速度啊,因为物体上滑的时候,他的加速度是不是朝都是沿斜面向下,然后你下来的时候是不是也是沿斜面向下,但是上去的时候,他的加速度是不是比较大 啊?水平上的加速度是不是比较大?那水平上加速度是不是比较大,说明他受到水平方向的重力是不是比较大?那你说水平方向的重力能给他产生水平上作用力吗?是不可以啊,只能是不是斜面 鞋先是不是只有鞋面跟他接触了?是不是鞋面对这个物体产生的力是不是比较大?那鞋面对物体产生的力大,那反过来呢?物体对鞋面产生的相应的力呢?是不是也是比较大? 那因此就是上滑的时候,物体上滑的时候,这个斜面受到物体的向右的力是比较大,所以此时地面对他的摩擦力呢,就是上滑时是比下滑时候大,最低是正确答案,答案选择的就是 d 选项 啊。看一下第三题啊,这个题是比较难的啊,因为对它受力分析啊,会比较麻烦一些,很多学生呢,在这里会出现错误啊,而且它的正确率是非常低的 啊。零点四,难度还是比较大的啊。我们看下这个题,如图所示,一个质量为 m 的 物体,恰好能够沿倾角为三十度的直角斜面匀速下滑。好,不用说了, m 就 等一个弹力 c 大 啊,弹力三十度角度,要告诉我们啊, 匀速下滑吗?你让物体在斜面匀速下滑的过程当中,在竖直平面内给它施加一个外力 f, f 以水平上的斜角为阿尔法,斜面呢,始终处于静止状态以至自动加速为 g。 下来说正确的事啊,我们先对这个物体啊进行这个受力分析,那物体呢?受到重力 啊,重力 mg, 还有就是支持力 fn 啊,那既然匀速下滑的话,那它的是不是还肯定受到一个鞋面对它有摩擦力啊?啊?鞋面对它有摩擦力 啊,这是我们是分析的是不受外力 f 的 时候啊,他因为他主要是分析啥是不是地面对鞋面摩擦力那因此我们把这个鞋面也拿出来分析一下,那假如鞋面啊,他的质量是 m 啊,他向下受到重力 是 m g 啊,向上支持力,我们给它记为 f m 啊,那你看雾块在向下滑的过程当中,它对鞋面的摩擦力是不是肯定沿鞋面沿鞋面向下它这个方向,这个记为 f 撇, 那这个这个雾雾块是不是对它会肯定会产生一个压力啊?这个压力啊,是垂直于我们这个鞋面啊,它是 f n 撇, 这个 f 撇和 f f n 撇和 f n 啊,它们两个是重力反重力啊,等大反向啊,等大反向。你在不施加外力的时候,我们先看啊,这个不施加外力的时候,它是不是可以匀速下滑,那匀速下滑也就是物体它和外力为零,那和外力为零任何两个力的合力是属于第三个力。等大反向 啊,这两个力的合力是不是数值向上大小是不是等于 mg 啊?等于 mg 啊?我们可以这样去理解啊,斜面对物块,它是不是有两个力啊?一个是 f n, 一个是 f 啊,它的合力是不是就 mg 啊?那我们是不是可以整体来理解,斜面对物块有一个数值向上的一个作用大小等于 mg, 那 你反过来呢?物块对斜面是不是也有一个 这个作用力啊,这个作用力是不是就是等大反向?是不是也是 m g 啊?因此在我们不施加外力的时候,这个 f 和这个 f 撇,它的合力 是不是竖直向下?竖直向下?好,那我们知道啊,沿斜面匀速下滑的时候,它的 f 摩擦力啊,是不是等于 f 的 f n 撇是等于 f n 的, 所以我们可以得出, f 撇它就等于 f n 撇啊, 反面。好,接下来我们就开始给他施加力了啊,看,当 r 法等于零的时候, r 法等于零,相当于这个小物块啊,它受到力是不是水平向右啊? 水平向右,当你受到水平向右的力,这个力是不是可以分解一个是不是沿水平方向的?你看这个水平方向的这个力是不是直接作用在小物块上了?它对这个斜面是不是不会产生影响啊?但是另外一个分力, 另外一个分力,这个分力啊,是不是会增加啊?这个物体对鞋面的一个压力啊?当你鞋面压力增加,那他的摩擦力是不是成倍增加?好,当这个鞋面他受到压力增加的时候,他的鞋面他这个摩擦力是不是也是成倍增加? 那你本来他的合力是不是还是竖直向下?那既然和力还是竖直向下,所以这个鞋面是不是不会 受到水平上的一个作用力,也就不会有水平上的运动的一个趋势?那因此呢,摩擦力是不是为零啊?不会向左也不会向右。看,当 r 法等于六十度的时候,那当 r 法等于六十度的时候,这个 f 不 就竖直方向去加吗?垂直这个斜面方向去加,那是不是也是相当于增加了这个 对鞋面的一个正压力啊?那当鞋面正压力增加的时候,你看 f 撇是不是也成倍增加,所以它的合力是不是还是竖直向下?那因此这个鞋面他是不会受到水平放的一个重力啊,那因此地面的鞋面摩擦力呢?是为零的? 好看 c 选项,当 r 等于九十度时候, r 等于九十度,不就数值,这个力 f 是 不是数值啊?作用在这个小 m 上?那刚才我们点力当中是不是已经分析了,你数值力增加在这个 f 上,相当于是不是这个物体的重力增加了? 那物体当 m 等于弹力随大的时候,他能够匀速下滑,你增加他的重力和他重力是不是没有关系啊?那所所以说这个物物块啊,是不依然能够匀速下滑,所以他是错了 啊。再看 d 选项,若 f 对 着雾块匀速上滑,那这时候我们就啊对这个,对这个鞋面啊,还是对这个鞋面进行受力分析,那这个鞋面向下啊,受到重力大于几? 还有就是这个地面对他一个支持力啊, f m 好, 现在你看这个雾块匀速上滑,所以他跟鞋面的这个这个摩擦力是不是朝这个方向沿鞋面向上 啊?好,还有就是这个物块是不是对鞋面产生一个压力,垂直垂直的鞋面方向是不是朝这个方向 啊?那你现在这两个力,这两个力是不是会让这个鞋面在水平上产生一个运动的趋势啊?那他他在河里是不是啊?是不是肯定有水平方向右的一个作用啊? 那你说物这个鞋面他受到了水平方向右的一个作用,那他既然水平向右运动,所以他给地面的摩擦力是不是也是向右的 啊?所以这个 d 错了啊,因此啊,这个题的答案啊,选择的是 b 选项。
44胡胖讲物理 06:01
06:01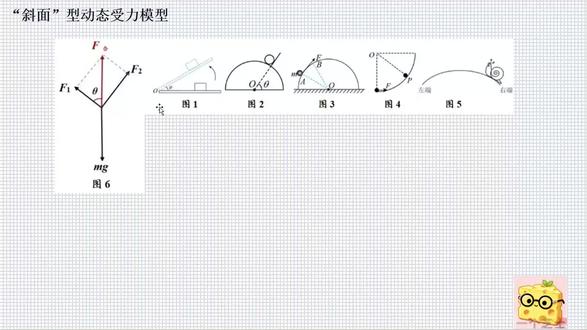 01:18查看AI文稿AI文稿
01:18查看AI文稿AI文稿三十秒教你从四科题变成四分题!今天讲高中物理斜面型动态受力分析, 那么这个模型主要描述的就是物体受三个力作用,除重力外的另外两个力方向在物体运动过程中始终保持垂直,这类问题称为斜面型动态受力模型。 常见的情形就如图一到五所示,处理方法与我们上个视频所讲的横竖斜形受力模型类似。那么我们具体把模型展开如何去分析呢?以图六为主。 由于 f 一 f 二始终垂直,则有 f 一 等于 m g cosine, 它 f 二 等于 m g sin sit, 当 sit 角增大时,那么 f 一 就减小, f 二则 增大。反之,当 sit 角减小时, f 一 则增大, f 二则减小。那么两个分力之间,我们满足 tangent sit 等于 f 二比 f 一, 你理解了吗?那么我们今天就讲到这里了,我是一个知识大家,下次再见了。
17一个芝士












