数学华容道5×5怎么画
粉丝5152获赞1.7万
相关视频
 01:58
01:58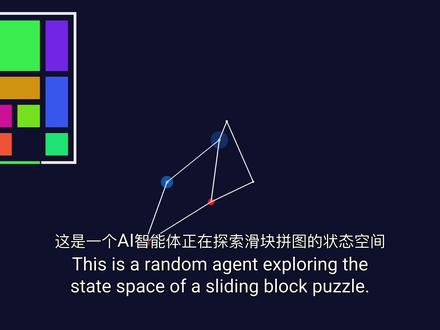 12:05查看AI文稿AI文稿
12:05查看AI文稿AI文稿这是一个 ai 智能体正在探索滑块拼图的状态空间。这个拼图游戏叫做 classkey, 这类滑块拼图相当普遍, 但除了作为益智游戏之外,这些滑块实际上定义了图结构,能够对复杂的拓扑结构进行建模,包括局部子结构以及局局超结构。 通常采用六乘以六网格,目标是将这个滑块从右侧缺口移出,目前还做不到,因为这块挡在路上。 让我们用节点表示拼图的当前位置。如果对拼图进行一次移动,就会到达另一个节点。由于这两个位置仅一步之遥,我们用边连接这两个节点, 每个节点都连接着若干其他节点,形成路径迷宫。你可能会好奇,如果加入所有节点,整个图会呈现什么形态。也许存在某种总体结构,比如网格,或者完全杂乱无章。 为了建立直观理解,先看几个设计的简单案例。单个滑块情况下只有一个运动自由度,两个滑块时,他们的坐标形成低卡尔机, 构成网格结构。每个滑块定义不同的运动轴。三个滑块构成三维镜格。当有四个自由度时,图结构自然延伸为超立方体。 但当滑块可以相互阻挡时,情况更有趣。以双滑块拼图为例,当滑块彼此相对时, 部分二维结构会失效,表示滑块重叠的情况。 当两个滑块在同一轨道时,会形成三角形结构,上方滑块的位置将决定下方滑块的活动边界。对于这类拼图,我们实际上构建了一个虚拟的对应结构, 对应着所有有效状态。这些状态必须通过方块相互穿越才能达成三块相交的拼图块仍构成一个立方,只是中间存在一些挖空区。 但随着拼图块数量增加,图结构的维度特性与拼图块数量的关联性显著,而与空格数量的关系更为密切。以这个拼图为例,它展现出有趣的特征,当完全展开时,可以看到整体存在宏观结构, 同时在局部区域也呈现出优美的规律性模式,就像各精致的二维欧几里德流行具有两个自由度,这是因为拼图上存在两个可供移动的空位,一个维度由顶部空位移动决定, 另一个维度由底部控位决定。在极端情况下,移动的不是拼图快,而是控位本身,他们决定了系统的自由度。因此,在完全填满和完全空置之间,拼图快之间会形成错综复杂的交叉结构。 这是我们最初研究的拼图之一,其宏观结构相当简单,不妨停下来思考它的可能形态。或许你能从拼图块的排列猜出它的形状。准备好了吗?从这个视角观察,拼图几乎是对称的, 关键在于要明白这两个部件会卡在两个固定位置中的一个,他们可以固定在红色竖条的左侧或是固定在右侧, 每次只能有一个进行状态转换。当红色竖条在上方时,橙色方块可以移动。而当竖条在下方时,绿色方块可以移动。这正是该图超结构的本质特征。 这是一个连接四角的方形结构,我们可以根据拼图块位置为图中的节点着色, 这一半节点表示绿色方块位于横杆右侧,另一半节点则表示橙色方块位于横杆右侧。让我们沿着这个图结构走一遍。 现在从这里出发,我们可以标出所有绿色方块靠近空缺处的结。 不出所料,这些结都位于绿色方块在横杆右侧的角落区。你能理解为何图形在角落处维度会升高吗? 再看这个 classkey 拼图,目标是将这个大块从底部移出。它与之前略有不同,因为交叉处没有固定销,所以方块可以横向自由移动。 相比上一个谜题,这个难度要大得多。我下班后给同事展示了这个拼图,但他不解开就不肯离开。他终于解开了。在晚上十一点, 他认为最困难的部分是将方块移到横杆下方。比起自己解题,我更想探究其背后的运作机制。将方块移到横杆下方真的是最难的部分吗?这个拼图定义的结构 究竟是什么形态?共包含两万五千九百五十五个节点。 由于拼图具有对称性,所以图形呈现。比如我们取这个位置棋盘就是该节点。在对称位置的镜像 旋转九十度后,可以看到大致被分为两部分。这个红色节点就是初始位置, 而这些是所有解,即方块位于底部的情况。所有解决点都位于与出使位置相对的图形半区。通过随机移动。 除非运气特别好,我们很可能会陷入这个密集的状态陷阱,重新回到初始状态。唯一的选择就是沿着这些精妙的路径到达另一侧。这条路径是最短解法路线,让我们跟随它。 有趣的是,这并不是吉尼斯世界纪录保持者使用的解法路径,他们选择了这条路径, 让我们验证我朋友的观点。解锁横杆是否是最具挑战性的环节。让我们高亮显示所有节点。 方块位于横杆上方时显示红色,并排时显示橙色,方块即将通过时显示黄色,方块完全通过后显示绿色。 现在让我们再次观察结法,准备可以看到近乎完美的重叠。看来我朋友的直觉是正确的。 我们还能发现什么?记得这个拼图存在不可达状态吗? plastik 拼图也是如此。你可能注意到,虽然图形是水平对称的,但为什么不是垂直对称呢?虽然在理论上可以将所有拼块倒置重排, 但实际上无法实现,除非取出拼块再重新放置,加入翻转棋盘和其他所有可达状态后,我们得到了完全对称的图形。 还存在其他孤立的状态群吗?事实上,数量相当可观,这是最大的一个,仅包含二百四十八个节点, 主要呈现为带有少量分支的长路径结构。 那么这个谜题的难点究竟在哪里?我们可以这样分析,难点在于方块通过横杆的步骤,或者说是两个半区之间的转换。困,但我认为这其中存在更本质的规律。 让我们观察一个遥远的区域,选一小部分节点进行观察。 现在我将展示所有这些节点对应的拼图布局,但采用叠加模糊处理,以便突出他们的共性特征。这个子结构中的所有拼图布局都有一个共同特征,方块和长条都位于中心位置。这个局部结构有两个空位构成,与我们之前看到的二维网格类似,但如果精确调整空位的位置, 就能跃迁到另一个具有独特规则和组织方式的子结构。 换句话说,这个图结构不应被视为单一的拓扑体系,也不是支配整个谜题的统一规则框架,而是一系列具有独立逻辑和形态的局部谜题 松散组合而成的整体。这有什么意义?谁会在意呢?不过是个玩具而已。 请允许我用图表做个类比。描绘自然界的现象图。在最顶层,我们看到生物超结构 建立在物理基础结构之上,通过多层次的抽象,关键在于这种现象解析度的分层并非物理学独有, 即使是最普通的家用玩具也不例外。这种形态正是通过对规则系统的计算探索自然涌现的。 我热衷于用计算机科学为各种系统提供全新视角。那些我们习以为常的事物,无论是复杂的滑块屏还是编程问题, 只要找到合适的视角,都能变得清晰明了。这正是 brilliant 课程如此高效的原因,通过游戏化的设计和清晰的案例,让亲身的知识变得一语掌握。 学会像程序员那样思考,将复杂问题分解为可管理的代码模块,或是直接上手 python, 从第一天就开始构建程序。 brilliant 祝你每日精进! 提供包含数学领域的数千互动课程,科学编程、数据分析及人工智能。这些知识并不晦涩难懂, brilliant 带您轻松掌握。立即体验 brilliant 全部内容,享三十天免费试用,年度订阅更享八折优惠。访问 brilliant 点 o r 详见简介中的链接或扫描屏幕二维码。本期 twoswap 由六千八百八十四配乐。
1.6万数理分享















