上饶市一模地理答案及评分标准
粉丝1.6万获赞6.6万
相关视频
 00:18查看AI文稿AI文稿
00:18查看AI文稿AI文稿试卷分享,高三全科高考模拟江西省上饶市二零二六届高三年级第一次高考模拟考试试卷及答案视频时长有限,展示的是数学学科部分资料,如有需要全部学科试卷加答案的,可以微长来取,整理不易。
 27:59查看AI文稿AI文稿
27:59查看AI文稿AI文稿好,我们来看一下这个十八题,十八题解析几何,他说已知有一个椭圆,它的焦距为二啊,然后 p 这个在 c 上面,椭圆 c 上面,第一问让我们求椭圆 c 的 方程啊,第一问还是很好解的,对不对? 好,我们来看一下,首先求焦距为二,是不是二? c 就 等于二啊, 对不对?那么 c 就 等于一,这个很好解释,对不对?好,然后呢,再干嘛?这个 p 一 到二分之三在椭圆 c 上面, 这个关键这个条件我们怎么用?我们可以怎么用呢?我们可以直接把它带进去,就是 a 方分之一加上四, b 方分之三等于一,就是把它带到这个椭圆的方程里面,然后通过呢?还有个式子,是不是椭圆里面有 a 方等于 b 方加 c 方,对不对?然后 c 方又知道就是等于一,所以说 a 方等于 b 方加一, 通过这两个式子去解 a 方和 b 方,这是可以的,没问题啊。然后呢,它还有一个方法啊,这个方法是什么呢?就是它既然焦点都给你了,对不对啊? f 一 f 二这两点都知道了,然后它一到二分之三,大概在这里 点 p, 既然这样的话,我们不妨用它的定义,用 p f 一 加 p f 二算一算它大,它大概是多少? 就算 p f 一 算 p f 二也是可以的啊。这里我们就主要演示这种方法,因为那种方法我在视频里面就是发那个卷子的,视频里面也已经说过了。好,首先看 p f 二, 首先 p 是 一到二分之三, f 二是一到零,哎,发现没有,这个 p 刚好是在 f 二上方的,对不对?所以说它 p f 二就是二分之三, 然后 p f 一 呢? p f 一, 你看这个 p f 二,譬如跟 f 二的作图坐标相同,所以说这个应该是个直角, 所以说,然后 f 一 f 二又是二,所以这是二分之三,然后这是二二,其实还是二分之四,对不对?二分之四,所以说 p f 一 可能求来就是二分之五啊,所以就二分之三,二分之四,二分之五,所以 p f 二就是二分之五。好,我写一下, p f 一 等于二分之五, p f 二等于二分之三,所以说 p f 一 加 p f 二怎么样?根据定义,首先它由数值算出来,等于二分之八,就是四,对不对?然后又定义它就是二, a 好, 所以 a 就 等于二, a 等于二, c 等于一,所以说 b 等于根号下 a 方加减 c 方等于根号三。好,所以整个的方程就是四分之 x 方加三分之外方 等于一啊。好,第一问就这么愉快的结束了,对不对?第一问还是比较简单的好看。第二位,第二位,他说如图存在斜率且不为零的直线, l 与 c 交于 ab 两点。好,我先把这个图拆掉 啊,交于 ab 两点了,然后有一个 f f 一, 然后 f 一 a f 一 b 的 斜率之和为零。好,求证 l 过定点 啊,这是个非常非常经典的模型啊。呃,其实这个东西二五届二五年的时候还没怎么考过,但是不知道为什么到了二六年就突然就开始考了啊,这个已经在去年的九十十一月份已经很多这个卷子考过这种类型了。这是什么呢?就是 如果这个是 f 一, 是负 c 到零的话,那么,呃,如果它们俩之和协力之和为呃定值的话,这个是过,我记得是负 c 分 之 a 方的。 对,负 c 分 之 a 方过。过。这个定点逗,零,这个是我在,我看一下是,呃,哪一天的视频,这个结论我是分享过的。 呃,我这个是在二五年的十一月十号的那个视频里面啊,我就有分享过这个结论,所以说大家如果不知道的可以去看一下,那个结论是很经典的。好,我们直接来证这个结论,这个这个题就是让我们证他过这个定点,对不对?好,我们首先 这个题我们肯定要设直线,设直线 ab, 关键是直线 ab 怎么设?我们我们有两种设法,就是 y 等于 k, x 加 m, 对 不对?还有一个什么 x 等于 m, y 加 t 啊,我们解释一下下面这种设法。下面这种设法是什么意思呢?就是说,比如说如果说你这个 y 轴上有个点二到零好过这条直线,那我们就可以设这条直线为 x 等于 m, y 加二。 为什么?你看,因为 y 等于零的时候, x 是 不是横等于二啊?哎,所以说这这种情况说法就是你如果有一个定点在 x 轴上,这用第二种说法会好一点。然后这个 y 等于 k, x 加 m 呢?是适用于有定点在 y 轴上的。 为啥?因为你 x 等于零的时候, y 就 横等于 m, 所以说你应该过零到 m 这个点,如果说你定点在外轴上,这样就很好表示啊,所以说我们这里就直接设。呃, l a b 是 什么? x 等于 m, y 加 t, 这样设啊,这样设。嗯,因为我们知道,其实我们提前已经知道它的,它的这个定点就是在 y 轴上。呃, x 轴上面的。 好,接下来跟他连立。好,连立,这里我再讲一个技巧啊,你不是四分之 x 方加三分之外方等于一吗?哎,这种分式就不要不要这个样子,我们干嘛?我们通通个分三, x 方加四,外方减十二等于零, 这是咋得到的呢?是因为这里有个四,这里有个三,看到没?四和三公倍,公最小公倍数是十二,所以说我们两边同乘十二,那就变成了三 x 方加四 y 方等于十二。好,化简来,就是这个东西。好,那我们就继续化解。所以说 三倍的 m y 加 t 的 平方加四, y 方减十二等于零。 好,这个时候我们再稍微化简一下,我们看哈,首先二次项,二次项,你看这是不是有个 m 的 平方外方啊?然后这还有个三,然后这还有个四,所以说外,那个二次项是三 m 方加四倍的外方。 好,你再看一次项,一次项,你看 m y 加 t 的 平方,是不是会产生一个二 m t y 二 m t y 同时要乘三,所以是加六 m t y。 好, 然后再看常数项,常数项你看 m y 加 t 是 不是会产生一个 t 方,然后 t 方这有个三,所以说三 t 方,然后后面有个十二, 好,等于零。好,这样就结束了,就我们把这个连立后的这个方程给写出来了。好,所以直接 y 一 加 y 二啊。尾答写一下, 这个尾答应该是很好写,对不对?三方加四。好, y 一 乘 y 二等于三, t 方减十二除以三 m 方加四。好, 我们就连累的部分就完成了。然后接下来就是表示斜率的问题了。好,嗯, 这里表示斜率,怎么表示啊?是不就是用呃, a 是 y 一 除以 x 一 加一,就是 a, 如果是 x 一 到 y 一 的话,然后 b 是 x 二到 y 二,对不对?然后再是 y 二除以 x 二加一, 然后因为 f 一 是负一到零嘛,它的斜率就这样表示的,然后呢,再把 x 一 等于 m, y 一 加 t, x 二等于 m, y 二加 t, 带到这个分母里面,就会成了一个值,行, 什么 y 一 y 二的式子,指行 y 一 y 二,那我们再通分怎么怎么样?是不是就可以用我们的尾答定理了呀?对不对?因为会出现 y 一 加 y 二和 y 一 乘 y 二这个东西,对不对?好,所以说 a 点我们就可以开始了, 都 y 一, b 点是 x 二,都 y 二好, f 一 点是负一,都零。 好,所以 k 一 等于 y 一 分之 x 一 加一, k 二等于 y 二分之 x 二加一。好, k 一 加 k 二等于 幺一除以 x 一 加一,加上幺二除以 x 二加一等于幺一分之 m 幺一加 t 加一,对不对?好,加上幺二分之 m 幺二加 t 加一。 好,那我们通分一下,首先底下就是它乘它,这个我就不用写了。然后上面应该是 y 一 乘 m 的, y 二加 t 加一, 然后加上 y 二乘 m, y 一 加 t 加一。因为这个题就通分嘛,就是因为你这两个, 相当于就是这两个就是底下的分母。然后呢,你由于这边是有 m y 一 加七加一的,所以说你要乘个它,然后你 y 二要乘个它,所以说这样好,它就等于零, 对不对?好,嗯,这个零我们放后面写,然后等于我,我过来一点, 好,我们再化简一下,好不好?我们再化简一下。好,底下分母就我不涂写了,我们来看啊,上面你看 这里是不是有,你看,首先这里有个 m 的 y 一 y 二,这里有个 m 的 y 一 y 二,所以说我们就化简一下就变成了两 m 的 y 一 乘 y 二,对不对?好,你再看这里, 你看 y 一, 这是不是有个 t 加一,这里出来 y 二,有个 t 加一,哎,你看,这也就是化简,最后化成 t 加一倍的 y 一, 加 t 加一倍的 y 二, 哎,那你看是不是这个时候就又可以干嘛?是不是就是加上我们 t 加一,提出来就是 y 一 加 y 二等于零, 对不对啊?哎,好了,这个时候你看它现在等于零,分母肯定不能为零嘛,所以只能分子为零,所以两 m 的 y 一 y 二加上 t 加一倍的 y 一 加 y 二等于零,到这里了。 好,然后呢,再我们代入回答,对不对?回答在这里,所以两 m 倍的三 m 方加四乘三, t 方减十二,加上 t 加一乘 负六 m t, 三 m 方加四等于零,哎,对不对?我们就有这个式子了。 好,这个是怎么再怎么处理呢?再怎么处理呢?你看哈,我们这里是不是,你看他们两个都有三 m 方加四啊?这个东西对不对?三方加四, 所以说干嘛?我们是不是就可以不要他了呀?因为他也是恒大于零的,我们要等于零五,相当于同乘个三 m 方加四,那是不是就变成了两 m 乘三 t 方减十二,加上 t 加一乘负六 m t 等于零,对不对?也就说这个三 m 方加四我们是不需要考虑的。好,最后化解,六 m t 方减二十四 m, 加上这里就减去了六 m t 方减六 m t 等于零。好,我们来看一下, 嗯,这里有点小,那个啊,好看,你看这个六 m t 负六啊,六 m t 方和这个负六 m t 方是不是消掉了?只剩了一个负二十四 m 减六 m t 等于零,哎,我们这时候发现是不是 m 也可以消掉啊,对不对?好, m 可以 消掉,所以说就是,呃,六 t 等于负二十四啊, t 等于负四, 哎,我们也就说通过我们这个 k 加 k 二等于零,我们求出来了, t 是 等于负四的,好,再看一下这个直线 l a b x 等于 m y 减四啊, 是不是?如果我们另外等于零的话, x 是 不是横等于负四啊?对不对?那所以意味着什么?它就横过零,负四到零 啊,这就是过定点的一个写法,因为你看这里,另外等于零的话, x 是 横等于负四的,不管 m 怎么变,所以说 这个是减 a b 就 过负四到零啊,然后这个第二问就这么解决了。那其实这个还是 很很常规的啊,很常规的。嗯,我们来看一下,再再来梳理一下。首先我们是射直线是 x m y 加 t, 这样射是为了后面表示那个,呃,那个定点表示的好,表示一点,然后连力好。首先第一个连力的细节就是这个 这个圆锥曲线的方程要把它整数化,不要用这种分式的写进去好,然后最后化简出来这个二一二元次方程,然后一元次方程,然后写出尾答。 写出尾答之后呢,我们就可以表示题目的条件了,题目条件是什么呢? k 加 k 二等于零,所以说我就把 k 一 和 k 二写出来好, k 一 加 k 二 好,然后呢,这里有个 x x 一 x 二,我不想看到 x x 二,因为我回答只有 y 一 和 y 二的关系,所以说我们就先把用直线 x 一 等于 m y 一 加 t, 也就说用这个直线 m y 一 加 t 给它表示出来哦,然后再加加加加 好,随后就通分,通分之后就变成这个东西了,然后,呃,另分子为零,然后最后再化解一下,这个基本上就差不多了。好也,这个就是这个题啊啊,其实你如果遇到复习复习的好的话,这块还是很轻松的,说实话,因为这个东西其实算是基本功了啊。基本功了好, 嗯,好,应该没有什么大问题啊,应该没什么大问题,关键就是这个 x 一 怎么消除这个 x 一 用 x 等于 m y 加 t 去消啊。 好,我们来看第二小问哈。第二小问,他说 f 一 b f 二 a 相加于 m, 要求证 m f 二减 m f 一 为定值。 有些人一拿到这个东西就有点呃,无从下手。他说这个 m f 二加 m f 一 为定值, 这个条件怎么翻译呢?对不对?好,我们就假设哈,我们假设它是个定值,比如说假如定值是二的话,哎, m f 二减 m f 一 等于二,这个条件我们熟不熟悉啊? 那么熟悉啊,为什么?这是不是就是双曲线的定义啊? 为什么?因为 f 一 f 二是定点,然后 m 到这个一个定点的距离减去 m 到另一个定点的距离是定值,这不就是双曲线的定义吗? 对不对?所以说,也就是说题目他告诉我们了,其实这个 m 的 轨迹是个双曲线哦,那你说他,他要求这个东西为定值,也就是说,也就是让我们解释他 m 的 轨迹是个双曲线 对不对?那 m 轨迹是双曲线,我们是不是要求出 m 的 轨迹来啊? 对不对?好,也就是说这个题从我们要证明 f f 二减 f f 一 为定值,最后就变成了什么东西,变成了让我们求 m 点轨迹的问题 啊? m 点轨迹的问题?好,嗯,接下来我们就可以做了嘛?好,我们来看这个 m 是 怎么生成的?这个 m 的 轨迹,你看它是 a f 二 b f 一 相交变成的,所以说,我们如果要求这个 m 的 轨迹,我们应该是怎么样?应该是连立 l a f 二和 l b f 一 这两条直线,对不对啊? 好,那我们来看一下啊。我们先打个小小的草稿, l b f 一, 我们,呃,其实第一问有错, y 等于什么? y 二分之 x 二加一,这是它的斜率对吧?然后它还过 f 一, x 加一,对不对?好,然后 l a f 二呢?那首先它的斜率是多少? y 一 除以 x 一 减一啊? x 减一对不对? 因为它过 f 二一到零嘛,所以就是这个样子的。然后呢,然后我发现一个什么问题啊?如果把这两个连立的话, 这个 y 二有,还有 y 二和 x 二, y 一 和 y x 一 这个变量太多了,对不对?那我有没有什么办法要就把它们统一呢?就是要么就只留 x 一 和 y 一, 要么只留 x 二和 y 二呢?啊,很显然这是有的, 因为这个题的第一问提示了我们 k 一 加 k 二的,你看我们是不是写了 b f 一 的条件, b f 一 的直线啊,就是这个 y 二除以 x 二 y 加一。哎,它是不是跟 fa 一 的斜率是相反的呀? 所以说我们 b y 一 这个 b f 一 的直线不仅能写成 y 二的条件,它还有一个方法,就是 y 等于负的 y 一 除以 x 一 加一倍的 x 加一。 哎,这样也来,如果我用这个形式跟 b a f 二这条直线连的,你看是不是就相当于轻松多了,对不对?哦,好的,那我们这样就我们就可以开始做了。 好,就可以开始做了。设 l a f 二, y 等于 y e 除以 x 一 减一, x 减一。 l b f e y 等于负 y e x e 加一除以 x 加一。好,接下来就是要连立,对不对? 连利有好,我们来看一下啊。首先,那我们连利怎么连利呢?有的人就直接 y 一 除以 x 一 减一,正 x 减一 等于负 y 一 除以 x 一 加一,被的 x 加一。啊,这个,这个消息还没关啊大家,呃,见谅一下,你这样连利也是可以的。然后呢, 我们再怎么求这个 x 好 一点啊,我们是不是把它做个比值啊?就是把这个 x 一 减一移到这边来。 x 一, 其实这样也可以吧? 嗯,然后就是,哎,其实这样有有有点,那个我们可以直接做比值。怎么做比值就是把这个东西移到这边来,这个东西移到这边来,那就是 什么 x 加一除以 x 减一等于 y 一 除以 x 一 减一乘负 y 一 x 一 加一等于什么?哎,你看这个 y 一 和负 y 一 是不是约掉了?就是一减 x 一 除以 x 一 加一,对不对? 好,那也就说 x 加一除以 x 减一,就是这个东西了。好,那么这个就好做了嘛。就是,那就是怎么做?再直接减一加二,就把它分一下,一加上 x 减一分之二等于 一减 x 一 分之 x 一 加一。好, x 一 减一分之二等于一减 x 一 分之 x 一 加一减一等于一减 x 一 分之 两 x 一 啊,所以这个这个就可以约掉了。那再翻过来, x 一 减一等于 x 一 分之一减 x 一 等于 x 一 分之一减一。哎,我们就发现 x 一 就等于,哎,这不是 x 一 减一啊,这是 x x x 是 不就等于 x 一 分之一啊?哎,把它解出来了, 大家可以看一下我这个呃演算的这个过程啊,看,请你看一下。好,那算,算出来之后呢? 是不是 x m 等于 x 一 分之一,那把它带进去 y m 是 不是就好说了? y m 我 就带到,随便带哪一个都可以啊,我就带第一个 x 一 减一乘 x 一 分之一减一等于 x 一 减一乘 x 一, 一减 x 一。 哎,你看,这可以消掉有一个负一就是负的 x 一 分之 y 一, 对不对?哎,这样,所以说我们的 m 点就表示出来了, x 一 分之一都负 x 一 分之 y。 好, 那接下来怎么样通过这个设置求出 m 的 轨迹呢?啊?其实,其实标答标答是怎么样的?到这里之后,它用这个设置去求 m f 一 和 m f 二,然后一减 啊,那样我觉得也是可以的。但是我还是想用求轨迹的方法去写好这个地方求轨迹,我们有个方法叫做反表示。 什么叫反表示?就是比如说你看 x m 不是, 那我就 x m, 假设为 x 零的话啊, x 零等于负的 x 一 分之 y 一, 我们想求 x 零和 y 零这个点的轨迹, 我们要,但是我们知道了 x 一 和 y 一 的轨迹,就是这个题,我们知道 x 一 到 y 一 的轨迹,我们想求 x 零和 y 零的轨迹,但是这里呢,又给了 x 零 y 零和 x 一 y 一 的关系,我们怎么样去 求 x 零和 y 零的轨迹呢?什么?就是用反表示?就是用 x 零 y 零去表示 x 一 和 y 一, 然后呢再把。呃,我们先这样求下啊,你看我们如果这样的话,你看这个 x 零等于 x 一 分之一嘛,所以说 x 一 是不是等于 x 零分之一啊?对不对?然后再把这个 x 一 等于 x 零分之一带到 y 里面去。 y, 呃,就是 y 一, y 一 不是等于负的 y 零 x 一 吗?那就等于负的 x 零分之 y 零。 哎,我们也就说我们用 x 零和 y 表示出了 x 一 和 y, 接下来怎么办?是不是又由于 x 一 y 满足这个式子呀? 是不是?那我们就代进去嘛,故四 x 零方分之一加上三 x 零方分之 y 零方等于一呀。 哎,你可以亲切的发现,这样我们就表示出来了 x 零和 y 零的轨迹了。好,我们再来化解一下这个地方,由于分母有 x 零方同时乘一下,所以四分之一加上三分之 y 零方等于 x 零方。 好, x 零方减三分之, y 零方等于四分之一。哎,四分之一,那我们所以说四 x 零方减三分之四, y 零方等于一。 哎,这个时候我们就惊奇的发现,我们求出了 x 零的轨迹,也就是 m 的 轨迹,就是这个。 好,这样以后呢,那么是不是就可以解了,那它的 a 是 多少? a 其实是四分之一开根号啊,因为这里是四 x 方,其实就是 x 零方, x 零方除以四分之一,对不对?好,所以说 a 就是 等于二分之一, 所以说 m f 二减 m f 一 就是等于二, a 就 等于一,哎,这样来,我们就把 m 的 轨迹 m m f 二减 m f 一 求出来了啊,好,这个就是整个的第二问的一个思路啊。好,关键就是这个反表示啊。首先,呃, 等一会,呃,我们最后再来把这个题梳理一下啊。梳理一下, 首先我们第二问,我们知道,我们首先通过这个 m f 二加 m f 一 为定值,我们知道它是个双曲线,通过双曲线我们就从定值问题转化成了求轨迹的问题。 求轨迹问题怎么办?我们是不是要先把 m 解出来呀?好, m 怎么解? m 由于是 a f 二和 b f 一 的交点,所以说把它们俩连立就可以得到 m, 然后我们连一的时候发现它会有一个 y 二 x 二 x 二的问题,那我们怎么样下去 y 二和 x 二呢?就是用 k 一 加 k 二等于零, b f 一 的斜率是负的, a f 一 的斜率。好,这样以来我们就可以把 m 用 x 一 和 y 一 表示出来了。 然后呢,这个时候我们发现它是带 x 一 和 y 一 的,我们怎么减回去?加,这个叫做反表示,我们用 x 零和 y 一 反表示出 x 一 和 y 一, 再利用 x 零和 y 一 在这个 x 一 和 y 一 在这个曲线这个曲线上解得 x 零和 y 零的关系,所以我发现它是个双曲线,解得双曲线的 a 好, 然后就没有问题了。好,整体就是这个样子啊。嗯, 所以说整体说实话啊,如果说这个基本上就议论复习的内容啊,如果说你复习的很扎实,这两个问是能够坐满的啊。这个,其实,呃,已已经是, 他是已经考过很多回很多回的了啊,好,这个是个经典的题啊,各位稍微看一下。
62欧皇许大仙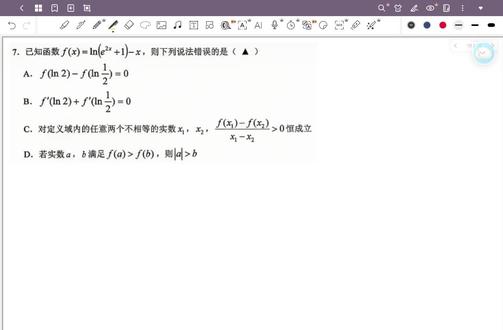 28:22查看AI文稿AI文稿
28:22查看AI文稿AI文稿好,我们来看下第七题,第七题他说已知有给了一个这个函数,然后让我们判断下列哪个是错的 啊?这个第七题的考点呢,其实是一个很经典的考点啊,这个函数啊,其实,嗯,它是一个很经典的函数啊。呃,我们首先来说一下这个题的考点是什么?它的考点是 单调性加奇偶性。 好,为什么这样说呢?因为这个函数啊,它是有这个函数,它是有个很奇妙的性质的,它是有奇偶性的啊,我们首先来看一下它到底是奇函数还是偶函数。首先 f x 等于 long 的 e 的 二 x 方加一减 x, 然后我们写下负 x 等于 long 的 e 的 负二 x 加一次方减加 x, 因为这是减负 x, 就 变成加 x 了。好,然后再把这个干嘛? 再把这个 e 的 负二 x 次方,是不是就是 e 的 二 x 分 之一次方啊?加一加 x, 因为它是负一,是指数,指数上面嘛。好,然后这个时候再通分一下 e 的 二 x 次方, e 的 二 x 次方加一,对吧,加 x, 哎,这个时候我们看一下 运用一个对数的一个性质,就是对数的减法, line 的 a 分 之 b 等于 line 的 b 减 line a, 所以 就分成了 line 的 e 的 二 x 四方加一减 line 的 e 的 二 x 四方加 x。 哎,你再看一下这个 long e 的 二 x 四方加一,还是不变的。好,这里就变成减二 x 加 x, 对 不对啊?我们看一下,就变成 long e 的 二 x 四方加一减 x。 哎,发现一个事情没有,它就是等于 f x 的, 也就什么意思啊,它 f x 等于 f 负 x, 它是偶函数啊,它是偶函数。好,其实做到这里呢,其实这个题就不用做了,就是如果你在考场上的话,因为 c 就 肯定错了。 为啥?我们来看下 c 是 什么意思啊?定义域内任意两个不相等的时数 x 一 x 二,有这个式子大于零成立啊,这个我们应该是在高一都很熟练了,这个大于零意味着它的意思就是 f x 横单增 啊,它是这个意思,但是你都是个偶函数了,你可能横单调吗? 大家想想,偶函数是不是有个对称轴?对称呐,所以他可能是这样画对不对?或者是这样画,也就是说他要么是单调,先递增后递减,要么先递减后递增,他不可能一直单调,偶函数是不可能一直单调的啊。所以说,其实到这里 c 就 错了 啊, c 就 错了,好,也就是说偶函数它是不可能单调的。好,所以 c 就 错了。好, c 就 错了。之后呢,我们 再来看一下啊 a 和其他选项吧。好,其他选项就是,呃, f 二分之一。我们先来看 a 啊, f 二浪引二减 f 浪引二分之一,这是什么东西啊? f 浪引二, 这是 a 选项啊,减 f 的 浪移二分之一就是负浪移二,对不对?那你看这是不是 f x 减 f 负 x 啊,对不对?那你说它是不是零吗?那肯定是零吗?因为偶函数的性质就是 f x 等于 f 负 x, 所以 a 就 对了 啊。然后 c 选项呢? c 选项考了一个知识。什么知识?就是如果说你 f x 是 偶函数的话,那么 f 撇 x 就是 奇函数, 这是啥意思呢?就是说如果你 f x 是 偶函数,那你求导之后那个函数就是奇函数啊。这个其实也很好整,因为我们偶函数不是 f x 等于 f 负 x 吗? 对不对?我们求个导,是不是就是 f x? 然后,呃,这里有个 f 负 x 求导,复合函数求导是不是有个负一乘 f 负 x, 哎,可以看可以看到,这就是我们 g 函数的定义,对不对?所以说 f x 就是 g 函数,所以 b 选项显然也是对的,对不对?哎,这写成 c 选项是 b 选项, 因为 f 二分之浪沿二和浪沿二分之一,它们是关于原点对称的两个,因为两个加起来等于零,所以说它们函数值加起来也肯定是零,因为奇函数啊,所以说 b 也就是对的了。 好, a 和 b 就 比较好换了。然后 d 选项 d 选项 f a 大 于 f b, 让你让你知道 a 和 b 的 关系,这考的是什么呢?这个其实考的就是它的单调性,因为你想啊,它如果有单调性的话,那是不是 f a 大 于 f, 不 就可以直接推出 a 大 于 b 啊?如果单调递增的时候,如果单调递减,就是 a 小 于 b 这个样子。 所以说我们看到这个,其实我们就需要研究函数的单调性啊。单调性怎么研究呢?呃,其实求导就行了啊,求导就行了,这个,呃,也不必多说,对吧?我直接求导好。首先 e 的 line 的 e 的 二 x 方加一,求导是 e 的 二 x 方加一好,然后上面是 e 的 二 x 四方求导二倍 e 的 二 x 四方减一。 我们来看一下啊,我们 e 的 二 x 方减一,除以两倍 e 的 二 x 方减, e 的 二 x 方加一,就等于 e 的 二 x 方加一啊,这是减一啊,这是减一, 减一,那就是 e 的 二 x 方减一。哎,我们看一下,这个底下这一块肯定是大于零的,我们就不用看了。那上面这一块呢?上面这块很明显它相当于是这个样子的嘛, 并且什么时候是零点啊?应该是零的时候是零点,而且然后他又是单调递增,所以说他就这样画的,所以说他相当于在零到正无穷,单调递增富无穷。呃,到零是单调季节啊,他的单调性就研究出来了,大概就是这个样子。画一下 零,零的时候是多少,零的时候是浪幺二,大概就是这个样子,就这个样子。所以说,呃,那既然 f a 大 于 f b, 那 这个数就是很经典的偶函数, f a 要大于 f b, 那 一定是 a 的 绝对值大于 b。 为啥?因为假如他们俩在同侧的话,比如说都在零到正无穷,那肯定是要 a 大 于 b, 对 不对?比如说 a 和 b 都大于零,他们都需要,所以叫 a 大 于 b。 如果 a 和 b 都小于零呢?那就是要 a 小 于 b, 对 不对?也就说 a 要在这边, 那如果 a b 一个大于零,一个小于零呢?那就是到零的距离要比,呃, a 到零的距离要比 b 到零的距离大。所以说总结起来其实就是 a 的 绝对值大于 b 啊,所以 d 也是对的。好,整个题就这么讲完了啊,其实在考场上选出来还是很容易的,如果你知道这个函数它是个偶函数,那你就秒出 c 是 错的, 但是讲我们还是要把它讲完。这个题考的就是一个奇偶性加单调性的分析啊。首先我们知道这个含判断这个函数是个奇函数,然后通过奇函数我们知道 a 是 对的,然后求导发现是偶,那奇函数,求偶函数,哎,刚才好像说错了, f x 是 一个偶函数,所以说 a 就 对了。然后在求导发现求导之后的函数就是奇函数,那 b 也对了。然后 c 就是 由于偶函数的单调性是不可能单调的,所以说 c 也是错的。然后 d 选项就是在研究一个单调性,发现它在零到正无穷是单调递增的,所以说,对呀, a 的 绝对是大于 b 啊,这是涉及到一个求导 好,这个题大概就是这个样子的。好,第七题讲完,我们再来讲第八题,第八题是什么呢?呃,我们来稍微选一下题啊。然后第八题说,已知正方体的棱长为四好,有个棱长 a 一 满足 a、 e、 e 等于一 好,然后 a、 c 与 b、 d 的 交点为点 o。 好 如如果有一个 r 法经过点 e 且与 o、 c、 e 垂直,则平面 r 法结的结面面积啊,这个题考的是个什么?是不是结面问题啊? 结面问题,我们的关键是什么?是不是就是要找出这个结面啊, 对不对?所以说我们现在就是要把这个前面找一下啊,找一下。好,然后我们首先来看一下题目条件啊,他说 a、 e、 e 等于一,一是四分之一哈,就是那个棱长的,所以说 e 应该在这里, 对不对?大家看这个这个图,然后 o, a, c 与 b 交于 o, 就是 底面的对角线。好,然后现在说阿尔法经过点 e 与 o、 c, e 垂直,然后则吧啦吧啦什么?好,那接下来我们就是要找到这个阿尔法,那怎么找这个阿尔法呢 啊?这里我给出一个思路,但是我其实,嗯,有点难解这个思路,我为什么是这样想的?就是我们首先要在这个结,这个面 a c e c a 找到,应该说是 a c 上面, a c 上面找到一个点,找到一个点,假设为 t 点, 使得 e t 垂直于 ceo, 好, 然后找到这个点以后呢?假如这个是 t 点哈,我再过 t 点做 b e 的 垂线,平行线。 好,做完这个,然后会交于两个点,对吧?那这两个点就是那个平面的就一部分, 就是这样找,就是首先找一个点 t, 使得 e t 垂直于 o c 这俩垂直,然后过 t 点做平行线, 好,首先来解释一下为什么这样就是这个结面,因为他这个结面他的唯一要求就是什么?就是与 oce 垂直,对不对?相当于是以 oce 为法向量的,那我们咋办?首先我们做了一个 e t 垂直于 oce, 那 是不是就是有第一条垂线了, 对不对?然后我又做了一个 b d 的 一个平行线,大家想 b d 和 o c 是 什么关系啊? o b d 与 o c e 是 不是垂直啊?然后我所以说我做了一个平行线,相当这条平行线也跟 o c e 垂直,也就是说我通过这个点找到了两条线,这两条线都是跟 o c e 垂直的,所以说由于我们的线面垂直判定的性质,那这个面就是跟这条线垂直了 啊,所以说找的就是这个样子。好,那我们接下来就是主要是找这个点 t, 这个点 t 到底在哪啊?好,那我们首先,呃,我们是不是要首先要把这个 a a, e c, e c 这个平面画出来, 因为 ac 在 上面嘛,然后 ceo 又在这个平面里面,所以我们要来画出来有点小歪, 根号二啊,这四四倍根二,根二,大概是五点六,要画长一点,嗯,一点五倍,哈,一点四一四,一点五倍,大概是这个样子的, 粗略的画了一下,啊,粗略的画了一下,画的有点小,小不准。 好,这是 a, 这是 a, 这是 c, 这是 c, 好, o 在 这里 o 是 中点,对不对?好,这有个 c, o, 好, 这里有一个四等分点 a e, 现在要找到一点 t, 使得 e t 垂直于 o c o c e, 这个咋找呢?其实这个跟十三题那个一样,就是要找那个相似,怎么找?你看 o c 是 不是二倍根号二,因为整个是四倍根号二吗? 对不对?然后二倍根号四加一是四,所以这个三角形的相似比是什么?二倍根号二比四,那就是根号二比二,就是一比根号二, 对不对?所以相当于 o c 是 一份 c, c 一 是根号二分,那我们要这样要再找一点,如果它垂直的话,那也就是说要什么?就是这个边是一份,这个边是根号二分,因为只有这样,这这两个才相似,相似完以后才有垂直。 好,那我们就看 a e a e 是 三三吧,对不对?所以说我们只需要找个根号二倍,那就是这里是三倍根号二,那很明显其实是中点嘛, oc 的 中点,对不对?所以,所以点 t, 其实就在这里把这 e t 一 连, 你就知道这就是个垂直的啊。当然如果说你不理解,你可以直接设点坐标,就呃, 你建个系嘛,然后设这个点 t, 因为点 t 在 a c 上面,可以设点 t 为 a 到 a 到零,然后把 a t, e t 向量和 o c 一 向量表示出来,数量积用 e t 向量乘 o c, 一 向量等于零,解出 a 好, 解出 a, 其实发现还是在这个位置 啊,所以说这这个就是找到 t 点的方法。好,那么我们这样的这样以来,我们就找到 t 点位置了啊,也就是说我们通过这个图就找到 t 点位置了,然后呢,我再给我 t 做一个 假如这是 t 点啊, t 点大概在这里再给我 t 点做一个 b d 平行线,哎,对,假如这是 e 和 f, 呃,还不能用 e 哦, 加上 g, 好 吧,那我们是不是连一个 eg, 连一个 e f, 那 这个面就是相当于就是面阿尔法的一部分,对不对?为什么是一部分呢?就首先它肯定是在面阿尔法里面,那它到底是不是面阿尔法呢?这个时候我们就要看结面的一个,呃,结面的一个 性质,就是结面的所有他的所有的点顶点都是要在这正方形的棱上面的 啊,我们看,呃,所有的线都要在这个正方形的面上面,就,也就说什么就是,嗯,我怎么解释啊?就是所有线要在正方体的面上面, 比如说我们看这个题, g f g f 是 不是相当于就在这个面上面,就在 a b c d 这个面上面,对不对?那这个这条线就不需要管了。但是呢,我们的 ef, 你 看 ef, 它是不在这个面上面的, ef 是 不在这个面上,不在面 a b a a b b 一 a 一 这个面上面的,所以说我们要就又要在这个面里面找一个点,然后也在这个平面里面啊,这是,这是这个洁面,所以说也就说我们现在找到其实只是洁面的一部分 啊,前面的一部分,所以我们还要把它扩一下啊,扩一下,所以其实这个题还是有一定难度的。有一定难度好,关键是怎么扩的问题的。好,这个我就又画了一个图,好,只要这个是 c 点。 嗯,大概这样扩了一下,关键就是怎么找,怎么找呢啊?首先,呃,这个就是找前面的方法了,就是首先我们离我们延长一下,跟 a b 交于一点,这个点叫做, 哎呀,画的有点,那个, 这画的太短了哈。 哦,他其实 是终点的位置,大概是这个样子的。嗯,对,大概是这个样子。首先我们要延长到这里来啊,画的有点丑,画的有点小,丑 点 s, 然后连接 a s, a e s。 啊, a e s, 哎,这里有个焦点,这里有个点, 这个点其实就是我们前面另一个扩展的一个点啊,这个就是扩展那个平面的方法。为什么是这样扩展啊?因为你想啊, 这条这条直线,我刚才算的这条直线是,他是不是在这个平面里面啊?在这个阿尔法平面里面,那我延长一下,他是不是相当于这条线也在阿尔法里面啊?然后我一交这条,这个点是不是也在阿尔法里面啊?然后竟然 a 一 点,呃,不不不,不不不,我连错了,应该是一点啊,一点, 我再连个 e s 点,既然 s 点在那个平面里面,那这个 e 点是不是也在这个 e 点也在这个平面里面,那你说是不是这这个焦点是不是也在平面里面? 哎,这样就找到了他的相当于他的延长另一个交点,然后另那个交点对面也是同理的,他其实是个对称的一个图形,所以说,呃,我们只要找到这一个点就够了。好,然后我们此时再连一下,连这里,然后 再连这里,最后再连这里。哎,算画的有点,那个相当于我们洁面就找到了啊,找到了,但是我这个图画的有点小丑哈, 那接下来我们就是要确定这个点的位置,确定这个点的位置,就是这个 b b 一 上面这个点到底是在哪里?那么首先要来看这个 g 和 f, 看上面这个 g 和 f 这个点在哪里?那我们画一个底面图, a b c d t 点在哪里? t 点是 o c 的 中点,对不对?现在这是 t 点,那我观察做 b 的 一个垂线,很明显这个这两点 g 和 f 应该是什么?应该是二终点的位置,因为这 c t 是 根号二嘛,所以说又是垂直,所以这是二,这是终点的位置。所以说你看啊,我们再过这个,我们刚才延长了一下, 交了一个这个点,这个点 s, 那 你看,由于我们这是个中点,对不对?接下来就是要找这个点的位置了。中点,所以说 这个 b s 其实也是二,因为这个 f b f s 其实跟呃 c f g 它是全等,所以 b s 也是二, b s 也是二了。之后呢?我们还要看哪个图啊? 我们还要看这个侧面,就是 a b b e a e 啊,其实这个是很复杂的,这这种找结面的方法是很复杂的, a b b e a e 好, 现在有个 s 点是一半, 相当于是 s 点,然后我 e 又一连。 好,假如这个点,这个点就是我们的那个结面的一个,那个顶点就是。假如是 y 点哈 y, 所以 说这个 b s 就是 二, ab 就是 四,那很明显,这个 我们想知道 b y 是 多少的话,那很明显 a e 它是六。呃三的话,由于你 b y 和 a e 是 这个相当于是相似三角形,这里有个相似三角形, 所以说是一比三的关系,所以 b y 就是 一,那 y 点就出来了,对不对?然后在那个面其实也 y 点,另一个面的点也是一样的,因为我们还过 g 点做一个那个呃结面的一个延拓,这里这个点,然后一连 这里这里有个 x 点,哈,这个 x 点也就是 d x 也是一,因为它其实跟这个 y 点的找法是完全一样的啊,所以说整个的图形就出来了,它其实是个五边形,是个五边形。我来画一下啊, 这里一二三四五,它大概是个五边形,然后这个五边形就可以求面积了嘛。 啊?求面积,但其实这种方法就很其实很复杂的啊,后面怎么求面积?就是只,那你就可以求了吗?因为他顶点各个顶点的位置都知道,我们就可以求了,所以说这个就是传统的方法,就是这样找结面啊,其实这个是很复杂的啊,说实话很复杂。 嗯,有简单的方法,有简单的方法就是要,但是要知道平面的方程就是平面的方程,嗯, 就是它平面方式是什么呢? a x 加 b, y 加 c, g 加 d 等于零,这个是平面的方程啊,这个就是一个平面的方程,并且这个 a 逗 b 逗 c 是发限量 啊。然后,嗯,那我就先把这个擦了啊,不擦,不擦,不擦,我换一面讲,嗯,这这种传统的方法是比较复杂,那我们接下来再介绍一下这个平面方程的方法 图,还是放这里?平面方程 就是什么呢?就是一个平面的方程啊,它是这样写的,是 a x 加 b, y 加 c, g 等于加 d 等于零,这是它的平面方程。然后呢,它的法向量 n 是 a 到 b 到 c, 也就说 x y 这前面的系数就是它的法向量。好,这个我我这里先不做证明哈,大家直接用就行了。好,那到这个题来是什么意思呢?你看啊, 这个点是一点的话,你看他说这个平面 r 法过一点,并且与 ceo 垂直,那我们想,既然跟 o、 c e 垂直,是不是就说明 o c e 是 法向量啊? 对不对?那这样我们是不是就可以解决 a b c, 对 不对?但是呢,他题目里面,呃,又说了过零斗过亿这个点,那是不是这个平面方程就可以写出来了,对不对? 平面方程就可以写出来了,然后就可以用用,用那个平面过亿点 可以写出来。什么地点?把把地给写出来啊?这应该是大写啊,这应该是大写,把地点给写出来, 那就是地求出来,地求出来以后,这个平面方是不是就知道了?这个平面的方程都知道,那我们想求这个结面是不是就好?很好说了。 就是,呃,比如说我们看他跟这个哪个面有交点啊?是不是就是直接用这个面的平面方程跟那个面的平面一相交,然后看交点不就行了吗? 对不对?好,我们再来写一下哈。首先我们先间隙吗?以 a 点的这个间隙,我就这个,这个我就不多说了,那就是 o 点,我直接写了二到二到零,对不对? c, 一 是四到四到四, 那么 o c 等于什么?二到二到四,对不对啊?二到二到四, 所以说 a 等于二, b 等于,嗯,其实这个可以缩小一点啊,就是一到一到一到二, a 等于一, b 等于一, c 等于二,这个等比缩小应该没什么问题。好,那么所以说这个方程就变成什么了, x, y 加二, g 加 d 等于零,对不对?好,那接下来又又又又,它是过这个平面过什么?一点一点是零到三,对不对?所以说什么就是, 哎,不不不,零斗零斗三,零斗零斗三,零斗零斗三,直接把它带进去,所以零加零加二乘三加 d 等于零好, d 就 等于负六,所以这个平面方程就写出来了, x 加 y 加二, g 减六等于零。那接下来就好说了嘛,就把它在各个面上面的这个点求出来就行了。比如说, 嗯,这个我看一下,比如说它 我们想一想,它应该是 a a 一 b, e, b 这个这个面上面有,然后呢? a, a, d, e, d 这个面上有,然后后面的这个 c, d, d, e, c, e 这个面上有,然后 这个 b, c, c, b, e 也有。把它们四个平面方上写出来,然后一解也是可以的啊,也是可以的 啊,然后我这里就不多展示了,这个就基本方法就是这个样子,然后,嗯,大概就是这个样子啊。所以说这个第八题,其实我个人认为是,就是整个单选加多选里面最难的一个啊,整个单选加多选里面最难的一个,最后答案算出来好像是七倍根号六,我记得是 因为他自己算一下就可以了啊,他,所以这个题就我觉得就有点难度啊,有点难度。他不管是算的方法还是传统方法,他要都要很复杂去做的话,确实有点有点小麻烦啊,有点小麻烦。
39欧皇许大仙 03:50
03:50 05:17查看AI文稿AI文稿
05:17查看AI文稿AI文稿好,我们来讲一下本次考试的一波卷子完成的闭卷啊,先看到五十六孔,这里呢有一个 art, 那 它是一个什么词性的词呢?是一个名词啊,后面我们看 combines, chinese and cambodian culture, 结合了中国和这个地方的文化。好,那你可以看出来它是一句什么呢? 用后面这一句话来形容或者修饰前面这个 art 这个名词,对不对?好,那它是一个什么?是一个典型的定语从句, 那我们说定语从句,你要往前看,对吧?它是指人呢?还是植物呢?植物就用什么,就用 that 或者是 which 都可以。好,再看这一句,我们首先是看选项哈,看选项看 leave, 那它是一个动词,那我们说看到动词的时候,你就要干嘛?首先判断出来它是谓语呢?还是非谓语? 你看这一句霖怡的 deep connection to calligraphy, 它和书法之间深刻的连接,你发现没,这一句话它其实是一个名词哈。好,那所以这个动词怎么样?它只能够充当谓语了,因为这一句话 它已经没有动词可以当谓语了。啊,所以它干嘛加 s? 那 为什么这里面一般现在是呢?因为你往前看 combines 是 不是也加了 s, 对 吧?所以它一整个段落哈,后面这两句都是在表述一个一般性的情况, 在描述一个客观事实。好,所以一般现在是加 s。 好, 再看到我是把控好 add, 对 吧?那我们会想起来一个句型叫 add something to something, 把什么东西加进去啊,所以这里填一个介词 to。 好, 我是九,看,这里。好,这里你是不是看到一个 before 呢?再往后看有一个 now, 对 不对? 再看意思哈,他说 before i loved the melody and the emotions behind it。 哦,我以前是喜欢这个歌词的旋律跟情绪的,现在呢?对不对? 有过去,有现在,表什么?表转折嘛?哦,但是现在我看到了什么?什么,对吧? ten but 表转折哈。好看。第六十题, 我们往前看一下啊,这个歌词对不对啊?一个东西啊, cross 你 发现没啊,是个动词对不对啊?穿过了田野和这个路对吧?都不用管啊,歌词穿过了什么地方那所以 cross 是 什么?是谓语? 那后面这个词怎么样?只能是非谓语。好,那我们又说非谓语呢?只需要考虑三个,对不对?他是目的还是主动还是被动好?他揭露了这个民族歌曲,你看一下啊,揭露民族歌曲 的根,对吧?的根。那是主动呢还是被动呢还是目的呢? 是主动对吧?所以干嘛加 i n g 啊?加 i n g。 好, 再往后看, right 是 一个动词对吧?还是一样?看到动词,我们先判断它是谓语还是非谓语,你看这里,在临沂写将近半个世纪以前, 这一句话是一样的哈,它也没有其余动词,所以这个 right 只能是当谓语哈。当谓语?那当谓语你要干嘛?你要判断语态?判断时态哈,它自己会写吗?这个歌那肯定不会是吧,不要被动啊,看时间。 时间是什么?是半个世纪以前对吧?哦,原来是被动语态下的一般过去式哈。 was written 这里要特别注意哈, written 是 双写 t 加 e n 的 哈, written。 好, 六十二题,那这个就简单对不对?名词 melody 前面用什么?用一个形容词去修饰名词 powerful 好 看,这里 这空哈,它跟这个 long 没什么关系哈,是另一个词。其实啊, lonely 表示渴望的意思啊,他们内心深处对于更好生活的渴望啊。 lonely 好, 再看这个哈,他说 princess janice jenny 去临沂啊,这个吉娜公主来到临沂的这场旅行对不对?像什么呢?两个文化之间的对话 是不是像一个对话?好像一场对话对吧?所以这一空填什么?填二哈,填二好,再看这一空, 你根本就不用往前看对吧?看这个词就好。 melody 名词好,名词前面一般什么?一般是用形容词来修饰名词啊?用什么?用一个动词的过去分词表示用词哈。 shade。
12上饶英语郑老师 01:08:49查看AI文稿AI文稿
01:08:49查看AI文稿AI文稿各位同学你们好,今天我们讲一下上老师二零二六届高三第一次模拟考数学四题,这份题目还是质量比较高,题目都非常的好。好,我们来一个一个讲一下。 第一题是集合的交集合,集合的并集是吧?并集就是这两个集合中的元素合到一起嘛,所以至少有负零一,然后 b 的 元素里面的元素 x 肯定有一个是负一, 那并起来就是这四个数了,所以这个题目选 c。 好, 再看下第二题, z 等于一加 i, 那 么 z 加一的 z 加一分之一的虚部,就一加 i 再加一分之一的虚部,那就是二加 i 分 之一。我们分母有理化嘛, 就分子分母同时乘一个二减 a 是 吧?那这里也乘一,那分子也乘个二减 a, 所以 分母是二四减 a, 一 方之五啊,就五分之二减五分之一 a, 所以 虚部是这个负五分之一,所以这个题目是选 d。 第三题, f 三 x 加一等于 x 加五的平方, f f 负二等于几?那我我们是直接令 x 等于负一啊,左边就是 f 负二,右边就是四的负一加五的平方,四的平方等于十六嘛,所以这个题目选 c。 第四题,这两个向量平行,那我们知道,就是这两个向量竟然都是 a 向量 b 向量的线型组合,那 a 向量和 b 向量前面的系数比肯定要相等了,就是一 除以 a 项前面系数一,要等于 b 项前面系数 m 大, 除以 b 项前面系数负一啊,所以 m 大 它就等于负一,所以第四题选 b 都非常的快。 第五题,将六个相同的小球全部放入三个,一定要是相同的小球放入三个不同的盒子里面,每个盒子都要有一个小球,那就至少一个是吧? 至少一个,那么不同的方法有多少种?这个叫这种排列组合。有是一个经典的方法,叫隔板法,是吧?就相当于这六个小球啊。一个六个相同的小球是吧?放入三个不同的盒子里面,你就隔两块板子嘛,你看下怎么隔? 隔两块板子就可以分成三组,每一组放到这个盒子里面去就可以了。比如说我这样隔也可以嘛?所以几种隔法呢?所以其实这个问题就是在 六个相同的小球里面隔两块板子,你不能在这里隔,在这里隔的话,那第一个盒子里面就没有球可以脏了,是不是啊?这格式就第一种隔法是什么? 是什么意思呢?就是在第一个盒子里面放两个小球,在第一个隔板和第二个隔板里面之间的球放在第二个盒子里面,然后第二个隔板右边的球放在第三个格子里面,是吧? 所以几种隔法呢?总共有几个空隙呢?这里一个空隙两个,三个,四个,五个空隙。隔两块板子有几种隔法就 c 五二,所以算下来就五乘四除以二就十种嘛。这是一种经典的隔板法,就是把两块板,把两块板子,是吧?把这六个小球隔 开来,有几种隔法呢?你随便都可以,怎么隔?隔成三份就可以嘛?好,这是第五题,所以选 c 第六题。 呃,这个是考指数跟对数吧,二的幺给四九等于 a, 我 们知道这个四可以写成二的平方九,然后这个底数的指数可以往前面提,变成什么?变成 倒数,是不是?所以等于二的二分之一,洛给二九,然后这个系数又可以放到真数的指数上来,是吧?是二的洛给二九的二分之一,是吧?就刚好九嘛,所以是二的洛给二三,这个底下了就是三嘛,所以这个 a 就是 三, 然后二的 m 次方等于九的 m 次方等于六,我们把这个指数改成对数,所以 m 是 等于 n 是 等于 n 九六,是不是?然后 m 分 之一加二, n 分 之一等于 b, 我 们利用那个换底公式, m 分 之一,它就等于 就把这个底数跟到真数换个位置嘛。落给六二,是不是同样 n 分 之一呢?它就等于落给六九 啊?就是对数倒一下,那他的增数跟底数就要换个位置嘛。好,所以 m 分 之一加二, n 分 之一,它等于什么? m 分 之一是若干, 呃,若干六二,是不是二? n 分 之一就是二分之一乘以 n 分 之一, n 是 若干六九,然后这个系数放到这个九的上面来,所以是若干六二加若干六三,所以是对数。加是等于增数乘,是不是 就落给六六?落给六六是一嘛?所以这个 b 是 一,所以 a 是 三, b 是 一,加起来就是四。所以第六题选 a, 这都是基础题,应该快速的把它做出来。 好,我们来看一下第七题啊。第七题 f s 等于洛音一的二, s 方加一减 x, 下面说法错误的是 a 选项。那你要知道 f 洛音二减 f 洛音二分之一是不等于零呢?我们知道洛音二跟到洛音二分之一,它是相反数的关系吧。 因为二分之一可以写成二的负一次方,这个负一又可以提到前面去,是负的任意二,所以这个 任意二跟到任意二分之一是负的关系,也就是你把它当,把任意 x 当 x, 把任意二当 x, 任意二分之一是负的 x, 所以 这个题目是看 f x 与 f x 的 关系,那就是看这个函数的什么性叫奇偶性。所以我们把 f x 写一下,看它跟 f x 是 不是相等嘛。 o 负 s 等于一的,呃,就是啰,隐一的负二 s 方加一, 嗯,加 x, 然后这两个相来相法呢?你一眼看不出来,看不出来我们就做减法,做叉是不是?做叉看它等不等于零嘛?做叉的话,对数减对数,那就等于正数相除,是不是? 然后这个负 x 减 s 就 减二 x 啊?然后我们把这个对数的增数分子分母同时乘以一个一的二 s 方, 把那个增数分母的分母把它去掉嘛,是吧?这个一的负二 s 方乘以二一的二 s 方,就是一的零,上就一啊, 这个底下了,是吧?若以一的二 x 方,就二 x 减二 x 等于零嘛?说明什么?说明这个函数的 f x 等于 f 负 x, 所以 这个函数 f x 是 不是偶函数? 它既然是偶函数,那 a 选项就对了,就 f x 减去 f x, 肯定会等于几啊?等于零,所以 a 是 对的好,那 b 呢?是导数,那我们知道偶函数,你要知道一个结论,是吧?就偶函数,你去求个导, 它就会等于奇函数。同样的,奇函数求可导,这是结论嘛?奇函数也就求可导,它就等于偶函数, 是这样的吧。对,好,那说明这个 f p x 它是什么函数? 它是奇函数啊,是不是?所以这个 f 撇 x 加上 f 撇负 x 就 会等于零呐,这个是 x, 那 这个就负 x, 那 所以这个 b 肯定也是对的。 c 对 于定义里面那两个不相等的数, x 一 x 二,这个东西大一点,我们知道这个分式一旦出现,就说明 f x 它在 r 上是正函数,是吧?这个东西就等价于 f x 在 r 上是正函数嘛。然后我们根据 这个函数 a 选项,根据这个函数单,它是偶函数,偶函数。图像关于 y 轴对称嘛,如果左边,如果 y 轴的左边是减的,右边肯定是真的, 或者如果 y 轴的左边是真的,那右边就是减的。也就总之这个 f x 是 偶函数,它就不可能在 r 上单调,是不是?所以这个 c 选项肯定是错的嘛,所以这个 c 选项肯定是错的嘛,所以这个 c 选项肯定是错的。 好,那 d 选项我们也来看一下了, d 选项它其实是考了这个函数的单调性,我们知道这个 f x 啊,它你看一下它单调单调性,你去求个导就可以了。导数等于什么?等于一到二 s 方加一分之, 这是对任意求导,还有对里面求导是两倍的一到二 s 方再减一,是不是?我们去分了一个常数嘛? 分离一个常数出来,那这里减二,是吧?再减一,这个除以,这个就是二,再减去两倍的一的二 x 方加一,再减一,当 x 大 于零的时候, 这个一到二 s 方是大于一的,所以这个分母是大于二的,那整个就会小于一。二减去一个小于的时候再减一,那肯定要大于零。所以这个函数它在零到正无穷是单调递增的。就这样发 啊,这样发,那在负无穷零是单调递减的,所以这个函数 f 图像应该是这样吧,是不是他现在说 fa 大 于 f b? 呃,比如说 b 在 这里啊,比如说,比如说 b 在 这里,那负 b 的 函数值跟它是一样的,是吧?那负 b 就 在这里,是吧?现在 f a 要大于 f b, 说明 a 要在 b 的 右边, 或者 a 要在负 b 的 左边,那不管在哪边,对 a 的 绝对值一定会大于 b, 是 吧?所以这个 d 是 对的。所以这个第七题选 c, 做题的时候选完 c 就 走人。第八题第八题是这个。 呃,结面,正方体结面的问题,正方体结面一定要把这个结面画出来,是吧?正方体 a、 b c d a b c d 临常式是能 a a、 e 上找一个点 a, e a, c, b, d 将有 o 点, 然后平面 r 法经过点 e, 而且以 o、 c、 e 垂直,那么平面 r 法截这个正方体所得的结面,这个我们就要把这个正方体去画一下啊。把这个正方体去画一下嘛。 假设这是 a 点,好吧? b 点 c 点 d 点 a 点 b 点 c 点 d 点,是吧?然后人长是四的, 在 a a 一 上,我们找一个点一点,使得 a 一 等于,使得 a 一 等于一,那么就要找四等分点了,大概在这里啊,我随便找的四等分点, a 一 在这里嘛。然后 a、 c、 b、 d 的 焦点是 o 点,然后把 a、 c、 b、 d 的 焦点画出来, 是 o 点,是这样画,是吧?然后平面阿法经过一点,而且跟 o、 c 一 要垂直,而且跟这个 o、 c 一 这条线要垂直,那我们就把以 o、 c 一 垂直的面找出来。先找,先找一条显而易见的以 o c 一 垂直的面是哪个面?以 o c 一 垂直的面,我们把这个 a e 的 终点 f 找出来,是吧? 以 o c 一 垂直的线,有一条明显的是这个 b d, 这个 b d 是 明显跟 o c 一 垂直的,然后我们把这个 b f 连起来,这个 d f 也连起来,这个绿色的面,它就跟 o c 一 垂直。为什么呀? 因为 o c 一 在左边这个面的摄影,摄影是谁?是 在这个点是 a b c d e f 点吧?这是 f f b e, 是 不是就这个 o c e 在 左正方体左边这个面的射影是, 是 f b f b e 跟 f b e。 哎,这个是 g 吧? g b e 跟到 b f 是 垂直的,跟射影垂直,就跟这条线垂直, 是这样的吧,所以 o c 一 还会跟这个 b f 垂直,所以这个 o c 一 啊,他就会把它擦掉去啊,就这条线,这条线我不要把它擦掉去了啊。 好吧,所以这个 o c 一 明显会跟这个绿色的面垂直,但是这个绿色的面并不是我们要找的平面 r 法,我们找的平面 r 法也要跟 o c 一 垂直, 但是他要过点一嘛,那我们就把这个平面 b d e b d f 把这个绿色的面移到过一点嘛,那就往上移一个单位就可以了,是不是?你去把这个呃绿色的面往上移, 移一个单位就可以嘛?移一下,所以这个 f 点移到了这个 e 点,然后 b 点往上移一个单位,嗯,往上移一个单位,就大概移到这里来了,是不是这个点是 g 点,相当于这个 b f 就 移到了这个 g 这里来,这是平面算法的一条线,是吧?然后这个 f d 也要往上移一个单位嘛,就移一下嘛。 好,所以这两条紫色的面就是面阿法啊,这两条紫色的面就是面阿法,那我们要把这个结面找找,找全了呀。好吧,那这个面阿法跟到什么? 那这个面阿法跟到前面这个面的交线在哪里?它要和这个 df 平行,是不是它要和 df 平行? d f 是 哪条线?我来画一下吧。 d f 相当于 d, f 相当于 d, f 相当于,嗯, 相当于这条线,是吧? d f 相当于这个是 z 吧? d f 相当于这个 c z 这条线,是吧?那我们要在这个前面这个面里面找一个过 g 点,还要和这个 c j 平行的线, 那我们是不是找 b c 的 中点成了中线,是吧?在这个三角形 b c 里面找个中线,我们假设这个是 m 点,好,这里一点, 这就把这个面阿法和前面这个面的交线找出来了,然后和右边这个面的交线呢?那就要跟 b f 平行,那是不是也要找这个 c d 的 中点?我们讲的这个点是 h 点嘛?找这个 c 的 中点 k 点,那把 h k 一 点这个 h k, 它就会跟, 它就会跟这个 g 平行嘛,是吧? 对,然后把这个 m k 一 连, m k 一 连,这个面阿法和这个正方体的结面,所以这个结面就是 g e, 呃, e h g e h k m 嘛?那我们求算它的面积啊,算这个紫色的结面的面积,那你把这个 g h 一 连就可以了。这个 g h, 它是,这个就相当于这个 b d 嘛。它是四四啊,它就四根号二,所以这条是四根号二,然后这一条我们算得出来是几啊?这里一连嘛,这就是四, 这里是二,所以是十六加四,二根号五,所以这条也是二根号五,是不是?那这个 mk 呢?是对角线的一半,是二根号二,然后这一条是几呢?是一,一是根号二,然后这里也是一啊一,二根号五啊,这里, 这里是一,这里是二,根号五,那这里也是一,这里也是二,也是根号五,所以这个五边形我们就把它编好了,二根号五,二根号五,然后这一条是 四根号二,然后下面是一个等腰梯形,是不是?等腰梯形,这里是根号五,根号五,然后这里是 二根二,是吧?然后你就可以把它算了出来嘛,我们做一条高,这里做一条高,是不是? 这里是二根二二,然后有个固定的,这里是平方,是二十,这里是八,就十二,所以这里是二根二三,所以上面这个三角形的面积是二分之一乘四,根二乘以二,根号三,这里约掉了嘛,是吧?所以是四根号六, 所以他答案其实已经出来了,肯定跟根号率有关了,而且不是是根号率,所以这个答案其实做题的时候就也就猜的出来。选 b, 但是我们还是把这个 下面这个梯形的面积也算出来吧,我们做一条垂线,是吧?做一条垂线,所以这里这一条是啊,根号,那,这条也是啊根号, 那,这里是根号五,那这一条用勾股定力,就是根号三嘛,所以下面这个梯形的面积二分之一,上底加下底就是六根号二,再乘以高根号三,所以算一下是三根号六,所以加起来就是这个结面的面积,是吧? 就是七根号六,所以这个题目选 b, 就 这个题目稍微难一点,因为这个结面好像比较难做出来,你要利用面面平行的性质,是吧?两个面啊,一个面同时跟两个面,跟两个平行的面相交交,线就平行。好,再看一下,多选第第九 d。 这个函数,我们用辅助角公式把它画一下,是根号一下 a 方加 b 方,根号一加一三 x 加 f, 这里 f 是 四分之一,所以 f x, 它就等于根号二三 x 加四分之一, 然后它是关于这个函数的说法。正确的是 y 等于 f x 加四分之 pi, 你 就把 s 加四分之 pi 带到这里来嘛,所以就等于根二三 x 加二分之 pi 等于根二 cosine x, 我们要考虑这个函数的单调性,是吧?啊,性质啊,最小正周期就是二派除以一啊,是二派,所以 a 错了。偶函数 cos x 是 不是偶函数啊?是偶函数,它这个根二呢?还是偶函数?所以 b 也是对的。 c 二分之三派零是不定于中信呢? 是不是这个函数过,它是过二分之三派零吗?而且这个点在 s 轴上,那就是对称中心吗?所以 b、 c 是 对的。 d 呢?在四分之派到四分五派是不是单调 d 减呢? 我们知道余弦函数,它的图像怎么画?余弦函数它是偶函数,它是这样画的,是吧?它在零到派上是单调递减的,然后派过去一点,它就是单调递增,是吧?从派到 二分之三派都是减的,你看这个四分之五派超过了派,所以啊,这个四分之派在这边呢啊,这里是四分之派,我们知道四分之派到派上是单调递增,所以这个 d 是 错的。所以第九题选 b c。 第十题, 这是三次函数是吧?这是三次函数,那么这个三次函数我们看一下这个函数再减二, a 减四,说明 f 二,它就等于 a 减四,你算一下,它确实是 a 减四,是吧? 对,那我们就要对加 a 选项,我们对加求和导导数等于什么?等于三 s 平方减六, x 加 a, 所以 f p 二就是导数的斜率,就切线的斜率嘛,就是十二减十二加 a, 所以 切线的斜率是 a, 所以 这个切方程我们套公式是, y 减去 f 二 等于斜率是 f 撇二乘上 x 减二,是吧?带进去嘛? f 二是 a 减四是吧?带移到右边来, f 撇二是 a 乘以 x 减二,再加上 a 减四,所以是 a x 减 a 减四吧,所以 a 是 对的,是吧?所以 a 是 对的, b 呢? b 它说 f x 有 两个极值点,那么 a 是 不是小于三? f x 有 两个极值点,说明它导数等于三 x 平方减六, x 加 a, 它等于零,说明它至少有两个根吧。 这两个根,而且是两个叫编号的根嘛。说明得大要干什么?要大一点嘛?得大等于 b 方, b 方是三十六减四, a, c 就 减十二, a 要大于零,那说明 a 要小于三,所以这个 b 也是对的。 好, c 形一样。呃,当 a 小 于零的时候, f s 是 不是有两个零点呢? 好,那我们把这两根假设是 x 一 x 二,我们把它极值点算出来,是吧?所以极两根之和是等于负的, a 分 之 b 等于二,两根之积等于 a 分 之 c 等于三分之 a 嘛? 两根之积等于二,两根两根之等于二,两根之积等于三分之 a, 这个是负的,是不是? a 是 小于零的嘛?说明一个根,他们这这两个根是一号的,是不是?我们假设 x 一 是是小的根,那他肯定小于零。零小于二, x 肯定要大于二,两根之合加起来等于二嘛,所以一个肯定要大于一个小于二, 是这样的吧。好,那图像怎么画呢?那你,那你算一下 f 零吗? f 零等于几? f 零是等于负 a, 它是小于零的,是不是说明 说明 x 一 是个极值点,而且这个三次函数图像是 n 字形,你要记得三次函数图像是 n 字形,所以这边是 f 零 f 零,这零的函数值负的吧?零的函数值是负 a, 负 a 是 负,负 a 是 正负的负 a 是 小零,负 a 是 正的啊,零的函数值是负 a, 负 a 是 正的嘛,所以它 它肯定是这样画,是不是?它肯定是 a, 它肯定是这样画,然后从在负无穷到 x 一 是增的嘛?而且它它零的函数负 a 是 正的,是不是? 那我们再算下 f 二 f 二值呢?负的 f 二是等于,根据 a 选项, f 二等于 a 减四,既然 a 小 于零,那 a 减四肯定是小于零的,就是二的函数值,它到下面来了,是不是?然后在, 然后它一直减到 x 二 x 二是几小数吗?对, x 二,看 x 二在这里是吧?在负无穷到 x 一 是真的,然后 x 一 到 x 二是减的,那 x 一 x 二就是极值点嘛,然后这边是真的 n 字形嘛?那它是不是有有几个零点,所以它是有三个零点,所以这个 c 是 错的啊? d 选项,当 a 小 于三的时候,这个直线与 f 图像是不是,是不是有三个不同的交点呢? 是不是有三个不同的焦点?我们看一下 这个这条直线过哪个点,有个参数 k, 那 我们就要找它过的定点,是吧?它过哪个定点,这条直线过定点到 x 等于一的时候,这个 k x 减 k 就 没有了,那 y 就 等于负二,而这条 而这个三乘函数 f x 等于 x 立方减三, x 平方加 a, x 减 a, 当 x 等于一的时候,这个 a 减 a 也没有了,他好像也是过,把一带上去,一减三也过一,负二 也是这个 n 字形也过,呃,比如说一负二这个点,然后这条直线也过一负二这个点,而且这条直线的斜率大零,那这条直线不管怎样画啊,他画一条直线, 他过这个三次函数的这个点啊,你不管怎样发,你不管怎样发,他都会和,在他斜率大于零的前提下,他都会和这个三次函数有三个交点,所以这个题目 d 也是对的。 abd, 我 们就这样定量的分析一下,就 d 选项定量的分析一下就可以了,看得出来这个 d 也是正确的嘛。 好,我们再来看一下这个十一题啊。十一题 他说时速对 ab 存在过一的直线和这条直线是交于 ab 两点的,而且 p 点是 ab 的 终点,就是 p 点是 ab 的 终点,是吧? 那我们就用钟点型公式了。还记得这个钟点型公式吗?钟点在圆锥曲线里面,椭圆三曲线、抛物线,它都有一个钟点型公式。什么叫钟点型公式呢?就是 o p 的 斜率乘上这个 ab 的 斜率,它是等于 椭圆是负的, a 方分之 b 方,商曲线是 a 方分之 b 方, o p 的 斜率, p 点是一嘛? o p 的 斜率就是 p 点跟 o 点的纵坐标之差,除以横坐标之差就是一啊,所以这个是一啊,这个一就没有写了,说明这个 ab 的 斜率,它就等于 a 方分之 b 方。 好吧,那接下来怎么办呢?我们就假设,那我们就可以假设直线 ab 的 方程,是吧?我们画一下商曲线吧, 上曲线这样画,是不是?所以我们可以画一条上曲线,它和这个交于 ab 两点是吧?一是它的终点嘛,所以我们可以设 ab 的 方程是什么? 我们可以设 ab 的 方程,是它过一一嘛。那就 y 减一,等于斜的 a 方分之 b 方乘上 x 减一,可以这样假设吧。 好,那我们把它化简一下,就是 a 方分之 b 方啊,我们两边乘个 a 方吧,就 a 方 y 方减 a 方等于 b 方, s 方减 b 方,所以就是 b 方, s 方减 a 方, y 方 加上 a 方减 b 方等于几啊?等于零。然后我们要确保这条直线和三角线有两个交点嘛,所以要连方程, s 方除以 a 方减 y 方除以 b 方等于一连方程, b 方 s 方减 a 方 啊,这里没有平方。直线的方程没有平方啊,这里没有平方。 y 再加上 a 方减 b 方等于零,是吧?那说明他的得量要大一点,是吧?然后我们可以用那个,那个公式叫等效判别式的公式嘛, 当然你可以直接运算,你用公式去套的话就很简单,套的话就是就是负的 a 方乘上 b 方的平方,加上 加上一个 b 方,乘上一个 a 方的平方,然后减去加上 c 方,加上 a 方减 b 方,这是平方是吧?还有大于零就可以嘛。 所以就是我们把它化解,就是负的 a 方 b 的 四次方,是吧?加上 b 的 平方, a 的 四次方,然后再加上 a 方减 b 方要大于零啊。然后这里我们可以提一个 a 方, b 方出来,就剩下 a 方减 b 方,是吧? 这是不是哪里写? 呃,再加上一个的这个平方啊, a 方减 b 方要大于零,是吧?我们提一个 a 方减 b 方出来嘛,就剩下一个什么?就剩下一个 a 方, 就剩下一个 a 方减 b 方加 a 方, b 方要大于零,是这样的吧。 那 abc 的 哪个正确呢?我们就带进去嘛。第一, a 选项,如果,如果 a 等于二, b 等于一,带进去行不行呢?那这里就是几啊? a 选项带进去就是,这里就是四减一嘛,然后这里是四减一,再加上一个 四,那肯定带进去,所以 a 是 可以的,是吧?所以 a 是 可以的。然后 b 你 把 b 选项带进去行不行呢? 你把 b 选项代入去,就 a 等于 a 和 b 等于四,那四减四等于零,那就等于零了,所以 b 这里就是零,所以 b 肯定不可以。 c 选项呢?你把 c 选项代入去就一样,那这里就是一减四,是复数,是不是?这边是一减四加 a 方, b 方再加上一个 一乘四,但是小一点不行吧,所以 c 也不行,那 d 肯定行了, d 自己弹一下肯定是可以的。所以十一题选 a d。 所以 这个就是考一个叫做钟点弦公式的啊。考一个钟点弦公式的, 然后记住一个等效判别式。等效判别是什么呢?就商学线的等效判别啊。椭圆的等效判别式是 a 方, a 方加 b 方。 我还是讲一下吧。就是就是一条直线和椭圆相交吗? s 方除以 a 方加 y 方除以 b 方等于。还有一条直线是 a 乘以 x 加 b 乘上 y 加 c 等于零,如果相交的话, 它的得答交大一点,那就等于什么?等于 a 方, a 方就是 a 方, a 方加上 b 方, b 方要减, c 方要大一点,是吧?如果是商曲线,就 s 方除以 a 方减 y 方除以 b 方等于一,然后这里是 a, x 加 b, y 加 c 等于零。如果相交的话, 它得大也要大于零,那就等于什么?等于加一,你就把这个符号提到这边来就可以了,就负的 a 方 a 方加 b 方, b 方加 c 方要大于零,这个叫什么?这个叫等效得大。好吧, 好,我们再看十二题,这个抛线的顶点到焦点的距离,抛线顶点到焦点的距离,我们知道是多少吧? 是这个系数的四分之一吧?是系数的四分之一,是不是?所以四分之 m 等于三,那 m 等于几啊?等于十二,所以十二题就是十二,这是送分的是吧?好,我们再来看一下第十三题,在边长为三的正方形,我们画个正方形吧。 正方形 a、 b、 c、 d 中 e、 f、 g 分 别在 a、 b、 a、 d 和 b、 c 上, a 一 等于两倍的 e、 b 对 一点,是三的分点了, a 一 等于两个 e、 b, 然后 e、 f 垂直。什么垂直 e、 g 啊?这是垂直的吗? 那么这个四边形 e、 f、 d、 c、 g 这个五边形的面积的最大值,我们在这个五边形面积最大值面积,它就等于这个正方形的面积。减去这两个小三角形的面积吧, 是不是正方形的面积是九,那我们减这两个小三角形的面积, 我们要求它的最大值,那我们就是求这两个小三角形的面积加起来的最小值嘛。好吧,然后我们看一下, 就这个三角形跟这个三角形是不是相似的?那肯定相似的,这是二,这是一。根据相似比,是吧?这个 a、 f 比上 a 一, 它会等于什么? 它会等于 b 一 比上 b 句,是不是说明这个 a、 f 乘上,对, a、 f 乘上加它相乘吗?乘上这个 b 句是等于 a, 一 是二, b 是 一,乘二等于二,是吧?我们假设这段是 x, 那 这段就是 x 除以二嘛,是吧?这个上角 a、 e、 f 的 面积呢?是二分之一乘以 二。底层高嘛?这个三角形 e、 b、 c 的 面积呢?是二分之一乘以二分之 x 嘛,是吧?所以等于九减去这里是 x 加上 四分之 x 嘛。好吧,然后这个,那我们, 哦,这里写反了呀,这两段乘起要等于二吗?你假设这一段是 x, 这一段就是 x 分 之二了,哎呀,写反了啊, x 分 之二,所以这里是, 呃, x 分 之一,是不是?然后这两段用积木来是大于等于两倍的两个相加大一等于两倍的根号下相乘呢?相乘就是一了,就是二,所以上面是大,这个跨里面是大于等于二,那九减去一个大于等于二的数是不是小于七啊?所以最大值是七,什么时候去等二啊? 当 s 等于一的时候去等号吧,是吧?当 s 等于一的时候去等号,就这里是一,这里是二,那这两个三角形的面积呢?都是一, 那就九减去二等于七嘛,所以等号是取得到的,所以第十三题是七。好,十四题呢?这个整数解的问题,整数解的问题,我们就把它去 去配方,是吧?要不然没法没法算。这个二 y 方减去二 x, y 减去一个二 y 加 s 方减二十四等于零,这个 s 方二 x y 和一个 y 方配成 x 减 y 的 平方,是吧?然后还剩下一个 y 方跟这个负 y 配配成 y 减一的平方,这边就要等于几呢?这边就要等于 多了,等于二十五,是不是等于五的平方啊?等于二十五,对,等于二十五。好,所以我们就分几几种呢?第一种情况是,是这个等于零啊,是这个等于零,这个就等于 正负五,是吧?第二种情况是,这个这个等于正负五,前面这个等于五,那这个就等于零,是吧?第三种情况是, 前面这个是等于正负三,那后面这个等于正负四,三的平方加四的平方等于二十五吗?第四种情况是,前面等于正负四,后面等于正负三就可以了。 好,那我们看有几个解呢?这个是两个解吧,是吧?两两个解。然后这里呢,也是两个解,就是 x 减 y 等于正五一个解, x 减 y 等于负一个解,是吧?然后这里是 x 有 两个, y 有 两个加,减就四个解, 同样下面的有四个解,这个 x 减 y 等于正负四两个解, x y 减一等于正负三两个解,二等于四个解,所以加起来是,呃,八加四十二个解,加起来是十二个解,所以这个十四题选的是十二十二个解。好吧, 好,我们再来看一下这个十五题。十五题是什么呢?是限性回归方程的题目是吧? 他说上饶市文旅局第五大热门景区,三清山婺源圩峰葛仙村望仙谷。哎,望仙谷还是比较漂亮的,我上次到了那里玩了一下。呃,风景比较漂亮,如果你们有时间的话去看一看。 呃。已知前五日每日的总游客接待量 x 和收入 y 的 相关数据,这里有五个数据是吧?建立第一问,建立 y 关于 x 的 限流方程, 并预测第六日三十万人次的时候输入,然后他这里给了限信回归方程的方程以及他的系数的计算方法。那我们套套就可以了,就套哪个公司呢?他给了这个数据,那就套这个公司是吧?等于 x i y 的 铝合这里都不给了吗?是一零三五吗?减去 n, n 是 五吗? s 的 平均数是几呢? s 的 平均数就是所有的 x 加起来是一百五十五,那 s 的 平均数就是一百五十五除以五吗?就是三十一,所以是三十一。 y 的 平均数呢? y 的 平均数你自己算一下就六七八六点五五点五的平均数嘛,加起来是几嘛?这里加起来是十二,加八就是二十,这里三十三,所以 y 所以 的 y 加起来是三十三,那 y 的 平均数就是三十三除以五。是, 是六点六是吧?六六点六吧。既然是六点六的话,那我们就可以把它算一下等于几 大一些嘛,所以这里是六点六除以。这个也告诉你了,是四八四五减去五 s 平均数的平方,那就三十一的平方,你自己去算一下,算出来就是 零点三啊。这个数字你自己去加减乘除一下嘛。那 a 是 等于 y 的 平均数,这里给了吗?减去 b x 的 平均数嘛? y 的 平均数我们算出来是六点六,减去 b, b 是 零点三, x 的 平均数是三十一,所以算出来是多少呢?是负的二点七。 所以这个第一问 y 关于 x 的 回归方程就是 y 等于呃,负二点七加上零点三, x 好,到 x 等于三十八的时候,你去估计一下嘛。当 x 等于三十八的时候,代取这个 y 等于几呢?负二点七加上零点三,乘以三十八,大概算一下是八点七。好吧, 就是第一问就算完了,比较简单嘛。第二问我们要算这个第二问, 他说这个望仙谷承载上限是五万人的概率是每天啊,每日的上限是概率是零点四,他说七天里面抽三天 既客客流量超过上限 s 的 天数,就 s 的 分不了期吧。那你就要把这个分布列划一下,是吧? 就是三天里面有几天有 x 天是流量客流量超过上限的,那可能 x 可能是零,就是一天都没有,也可能是一,也可能是二, 也可能是三,是零的概率是几?它每天超过上限的概率是零点四。码就是 c 三零 超过的概率是零点四,没有一天,那就零次方啊,那没超过的概率是零点六,几天呐?三天嘛,那这里就是 c 三一超过零点四超过一天嘛,那零点六就是平方啊,这就是 c 三二零点六没有超过一次,零点四超过两次嘛, 那这里就是 c 三三零点四的立方嘛。这个 x 是 不是超级要分布,是吧?超级要分布相当于做 呃,不是超级样本,这是二项分布吧,是吧?二项分布啊,这个 s 服从二项分布,相当于做三十多次重复试验,每次试验成功的概率是零点四嘛。那期望呢?我们知道期望服从二项分布的期望是等于 n 乘上 p, 就 试验的次数乘上每次试验成功的概率,所以等于一点二。 所以 x 的 分布列数学期望就是一点二嘛,相当于这个二项分布。这是十五题。好,十六题啊,十六题,让我看下十六题啊。第一问,它平面四边形 ab 等于 ac, 等于 cd, 等于二角 a、 d、 c 等于三十度,那这个角就是一百二十度是吧? g、 s 三是吧?角 d, a、 b 是 一百二十度,那说明这个角是直角九十度是吧?好,第一问,呃,将三角形 a、 c、 d 翻折,沿着 a、 c 翻折到 a、 c、 k 满足 k、 c 垂直 ab。 求证,平面 k, a、 c 垂直,平面 abc 要正面,面垂直,那根据判定力也要正到一个面,经过另外一个面的垂线吗?哪个面有垂线?我们现在知道 ab 是 垂直 ac 的, 因为这个角是九十度,是不是?然后他又告诉你这个 ab 是 垂直 k、 c 的, 根据这两条,那就可以推出 ab, 他 就会垂直过 ac 和 k、 c 的 面,那就是垂直于面 a、 c、 k 是 不是?那 ab 在 这个面 a、 b、 c 里面,所以就可以推出来面 abc 就 会垂直面 a、 c、 k。 好, 第一位就算出来了是吧?第二位呢? 第二问,求面 a、 b、 k 和面 c、 b、 k 它夹角的一个圈圈,那这个我们间系去做就可以嘛,是吧?我们这里做一个 c 组嘛,然后这里做一个 s 组嘛?这里,这里做一个 y 组,这些 这些坐标都很好写吧,是吧?然后这个简单题我就不算了啊,这个非常的简单,自己建个细去写一写就可以算出这个 答案嘞。我就不算了啊,就等于七分之二十一,这个非常简单,我就 pass 了。好,我们看十七题吧。 第一问,递增的等式列满足 a 一 加 a, 二加 a 三等于九, a 一 乘 a 二乘 a 三等于十五,那不就是一三五吗?是吧?所以这个 a n 就 算出来了,是一三五,那就是公差,是二嘛,那就是二 n 减一嘛,这不就做出来了吗?非常简单。第二问, b n 是 正数, b 等于二,而且满足这样一个递推关系吧。那我们就可以提一个,就前面两串,我们可以提一个 b n 出来,就剩下两倍的 b n 减去 b n 加一, 右边加上两倍的 b n 减去 b n 加一,等于几啊?等于零。我们再提一个两倍的 b n 减去 b n 加一出来。 呃,那还剩下 b n 加一等于零吗?这个是因为 b n 是 正数,这个是不为零,那就它等于零,是吧?所以 b n 加一,就会等于两个 b n, 也就是 b n 加一,除以 b n 等于二, 这是个常数嘛。那就说明什么?说明这个向量 b n 是 等比吧,说明向量 b n 是 以公比为二的等比数列了,是吧?然后 b 等于二,那就可以把 b n 算在 b n 等于二的 n 次方嘛,就算出来了,是吧?好,第一问,第一问,就是套公式,把它套出来就可以了。看第二问, c n 等于什么呢?等于 b n, b n 是 二的 n 次方, n 是 基数的时候,是吧?然后 c n 等于 a n 减一,乘上 a n 加一, a n 减一,那 a n 减一就是二, n 减三嘛, 乘上 a n 加一就是二, n 加一嘛,分之一嘛, n 是 什么? n 是 偶数,是不是?我们把它化简一下吧,二的 n 次方就不用化简了。 n 是 奇数,这个可以化简成列项,这个可以列项,是吧?分母相差四,那列项就成个四分之一啊, 就变成二 n 减三分之一减去二 n 加一分之一。 n 是 什么数? n 是 偶数,是不是我们要求 c 二 n 的 前二、前二 n 项和 t 二 n 嘛?那你写一下吧, t 二 n 等于什么?我们把这个基数项放一起,偶数项放在一起,是吧?就 c 一 加 c 三,一直加到 c。 什么二 n 减一嘛, 然后右边呢?是呃,把偶数放在一起, c 二加 c 四一直加加到 c 二 m 嘛,是吧?然后这个,这个是什么?这个是带哪个公式?带这个公式基数嘛,是吧?但是 c 一 c 三 c 五嘛,这是公比为四的单位数点,是吧?这是公比为四,因为它中间隔了一项是一减公比分之首项是 c 一, c 一 是二,然后一减四的 n 值方就可以了。然后这里是列项嘛,列成 提个四分之一出来, c 二,你就把二减去嘛,就是一分之一减去五分之一, c 四把四减去五分之一减去 九分之一,是吧?一直写写到 c 二 n, c 二 n 是 几呢? c 二 n 是 四, n 减三分之一减去四 n 加一分之一嘛,然后中间都抵消了,是吧?列向的目的不就是为了抵消吗?所以这是三分之二乘上四的 n 次方减一, 然后后面是加上呃,四分之一,然后一减去,它就是四 n 加一分之四 n 约掉去,就答案嘛,所以答案是三分之二乘上四的 n 次方减一,加上四 n 加一分之 n, 这不就做完了吗?好,这是十七题,我们就讲到这里啊。 好,我们再来看十八题啊。这个圆锥曲线的,你看一下,这个椭圆的焦距是二,焦距是二, c 等于二,说明 c 等于一,是吧?然后 p 点在椭圆上代入去,就 a 方分之一,加上 九除以四, b 方等于一,然后 a 方减 b 方等于 c 方等于一。就看得出来, a 方他就等于四, b 方他就等于三。所以这个商学的方值是 s 方除以四加 y 方除以三等于二。第一位我就做出来了吗?第二位, 斜力存在且不为零的直线二,这条是直线二,以椭圆交于 ab 两个点, f 一、 f 二分别是左右焦点 f 一 a 的 斜力和 f 二 b 的 斜力是 k, k 加 k 等于零,说明这个斜力是负于相反数,说明这两条直线的切角是互补的,是吧?第一,半正直线二过定点。 这种题目,我们为了简化运算,可以叫平移其次化,是吧?叫平移其次化。我们把,呃就是平移,把谁当做变量? 既然他是 f 一 a, f 二 f 一 b, 他 共了个 f 一 点,我们把 f 一 平移成什么?平移为作变量,这样的话就可以 简化运算,是不是就是这样的?是吧?这个 f 一 点原来是几啊?原来是负一零,经过平移之后变成了什么? 变成了 f 一 撇点,它就变成零零。所以原来的 x y 跟现在的 x y 有 什么? x y 撇有什么关系?原来的 x 是 等于现在的 x 撇减一,原来的 y 就是 现在的 y 撇,是吧?所以这个椭圆的方程呢?是不是也变了?所以在什么呢? 在新的坐标系下,在新系下,这个椭圆的方程就不是 s 方除以四加 y 方除以三等一了。这个椭圆的方程是 s 撇,减一的平方除以四,加上 y 撇的平方除以三等一。 好吧,同样,我们再先下假设这个直线 ab 的 方程 是 mx 加 mx 撇加 ny 撇等于一,这样话好,算一点,好吧, 我这个撇我后面就不写了啊,我们后面就不写这个撇了,我们去连方程,是吧?连方程就是四分之,我们把分母去掉吧,就是三倍的 x 减一的平方。我把这个撇不写了啊, 好,这个 m x 加 n y 等于一。好吧,我们把它算一下,得到什么?就三 s 方加四 y 方,然后这里是 减六 x 是 吧?再减九等于零。我们其次话嘛,就三 s 方还是三 s 方,四 y 方还是四 y 方,减六 x 就 乘以 mx 加 ny 嘛,九就减去九倍的 mx 加 ny 嘛,平方嘛。因为这里都是一嘛, 就乘个一乘个一的平方,数值是不会变的,是不是?然后我们就可以写成四 y 方,是吧?四 y 方加几 y 方呢?加一个,这里长个,这里长个,还一个 y 方,就是九 n 方 y 方,是吧? 嗯,就是这样的。再加上什么呢?再加几倍的 x y 呢?这里有六 x 乘以 n y 就是 六 n y, 六 n s y, 然后这里再加上一个什么,这里展开来有一个二 m n y, 就 加上十八 m n x 乘以 y, 后面就是加 s 的 平方啊,等于零,是吧?然后我们两边同时去除一个, 我们再画点一下,就九 n 方加四 啊,减四啊,这里是减了,这里是减去九倍的 n 方 a 方。哎呀,这里是减,哎呀,减,这里是减啊,不要写错了,减。 呃,那这里也是减嘛,这里也是减了,是吧?所以把它写成四减去九 n 方 y 方再加上一个。呃啊,这里也是减。哇呀,这里也是减,这里也是减,减去一个,加上一个。负六 n 减十八 m n x y 再加上多少倍的 x 的 平方等于零,是吧? 对,我们两边同时去除一个 s 平方吧,这就约掉了,是吧? 这,这,这就没有了吗?就是一吗?好吧。然后我们他的,他的根,他的根就是这个 s y s x 分 之 y 的 根吗?他不就是他的根,不就是那个 k 一 k 二吗?所以我们用两根之和,是吧?两根之和等于零吗?两根之和等于负的 a 分 之 b 就是 四减九 n 方分之六 n 加十八 m n 又等于零,是吧?说明这个六 n 加十八 m n 等于零。 我们可以约掉一个 n 去,就是六加十八 m 等于零,所以 m 等于负的三分之一,所以这条直线的 m 等于负三分之一,是吧?就负三分之一 x 加 ny 撇等于一,所以他过哪个点到 x 等于到 y 等于零的时候, x 等于负三,他过负三零这个点,这是在新坐标系下,是吧?那么在老的坐标系下,他过几 就是 x 等于 x 撇减一嘛,负三减一就是负四,所以在老的那个坐标系下,它是过负四零,这就算出来了。所以直线二过定点,这个定点是负四零。好,我就讲完了啊,这个,这,这个求过定点呢?我们 就协力之额,关于有协力之额,协力之积的这样的问题啊,我们一般用平移奇次化就很容易算了啊。好,我们再来看一下第三问吧,它的直线 f 一 b 和 fa 焦点是 m 点 m 点,求 m f 一 减 m f 二是个定值。好,那我们就直接算了,这个就没有办法。我们假设直线,我们假设直线 f 一 b, 它的方程它过这个负一零,是吧?那就是 y f 一 b, f 一 b 的 斜率是 k 二,是吧?就 y 等于 k 二乘上 x 减负一加一,然后 k 二等于负的 k 一 啊,也就 y 等于负的 k 一 乘上 x 加一, 是吧?直,这是直线 f 一 b, 然后直线 f 二 a 呢? f 二 a, 它的方程怎么写?直线 f 二 a 的 方程怎么写? f 二 a, 我 们假设 a 点的坐标是 x 一 y 一, 可以吧?它的方程是 y 等于什么?这个 f 二点的坐标是一零, 是吧?所以这些 f 二 a 的 这个 k 等于什么? f 一 b, 这 k 一 等于什么? k 一 是 f 一 a 的 斜率嘛?是吧?它是等于负的 k 一 k 一 是 f 一 a 的 斜率, f 一 a 的 斜率等于什么?就这个 k 一 啊,是等于 f 一 a, f 一 a 就是 y 一 加一除以 x, 这个是负一零嘛?好像 y 一 就是 y 一 除以 x 一 加一,所以这就是等于负的 y 一 除以 x 一 加一,乘上 x 加一。好,这是直线 f 一 b 的 方程。 好,同样的道理,我们去写直线,是吧?同样的道理,我们去写直线 f 二 a 的 方程。 f 二 a 的 方程就是 y, 它的斜率是这两点的重坐标之差 除以横坐标之差,然后 x 减一,是吧?然后连这两个方程,我们就可以算出 m 点的坐标,是吧?去连立一下,把这个 m 点的坐标算出来,可以吧?你去连,我就不连了啊。这个就直接算一下,算出来 m 点的坐标是 x 一分之一,然后负的 x 一 分之 y, 是 吧?那你就可以算 m f 一 的长度啊,用两点间的距离公式算 m f 二的长度啊, 就很容易算的啊。算出来是四,我就不算了,你自己算一下啊,四加 x 一 除以二 x 一 的绝对值, m f 二的长度呢?就是四减 x 一。 哎,就是点到,就是用点到点的距离公式去去算一下嘛。好吧, 用点到点的距离公式,你去算一下就算得出来嘛。这就是四减 x 一 除以二 x 一 的绝对值。所以 m f 一 m f 二减 m f 一 等于什么? 就等于二 x 一 的绝对值,是吧?就它减它嘛,因为 x 一 肯定不会超过四,就四减 x 一, 再减四,再减 x 一 x 一 是负的嘛,是吧?所以这个四根是约掉了嘛,是吧? 就是负二 x 一下面也是负二 x 一 x 一 是个负数嘛,看图嘛,所以它等于一,所以这个定值是一。 好,这是第二问。我们就这么简单的讲一下这个连力的过程,这个计算的过程我就没有去算了,你自己去算一下就可以了。好吧, 好,这是这个十八题,然后这个压轴题,十九题呢?那我们来算一下吧。这十九题稍微复杂一点啊,就是 你可以自愿性的选择放弃啊,会做第一问就可以了,第二问,第三问不会做。嗯,影响不会很大,除非你考清华北大,你就把它做出来,你考一般的,一般可以自愿性的把第二问,第三问放弃,是吧? 好, f x 等于什么呢?等于三 x, 第一问呢,就零到九十度的时候, f x 等于三 x 加 tangent x。 tangent x 是 什么?是三 x 除以 cos x 是 吧?好,那第一问呢,我们就减,把右边的移过来嘛。我们假设一个函数, g x, 可以 吧?等于这个 sin x 加 sin x 除以 cos x, 再减二 x, 你 求导是吧?导数等于什么?呃,三 x 导数是 cos x 吧,然后这个分母线平方上导下不导就是 cos x, 减去上不导下导就加 cos x, 是 吧?再减二就是 cos x 加上 cos x 平方 x 分 之一, 再减二,然后去通一下分嘛,通成 cosine 平方 x, 那 这里就 cosine 立方 x 减二, cosine 平方 x 再加一啊,这个通分正负的呢? 呃,我们可以把它化解一下,这里要注意分式因式分解的步骤。好吧,我们把减两个 cosine 平方 x 写成减一个 cosine 平方 x, 再加上一,再减一个 cosine 平方 x, 可以 吧?呃,这样写会不会好一点呢? 好,这里提一个扩散屏幕 x 出来,就剩下扩散 x 减一,是吧?然后这里加上用平方它公式一加扩散 x, 再乘上一减扩散 x 嘛,就可以了。我们再提一个,呃,一减扩散 x 出来,好吧, 那这里就剩下个一加扩散 x, 再减去扩散屏幕 x 吧, 是吧?再除以 cosine 平方 x, 你 就发现都是正的吧。你就发现这些这个是正的, 一减 cosine x 也是正的,这个一减 cosine x 也是正的。就这两个相减是正的。 cosine x 是 正的,所以加起来是正的,所以它大于零。所以这个 g x 在 哪里?在零到二分之派是单调递增的,然后你算下 g 零, g 零等于三以零,呃,加上 tangent 零, 再减个零等于零,是吧。所以一开始它的函数值等于零,然后又是这样递增的,说明了 g x 一 开始是零,但要递增,那大于零是不是还是零?所以就证到了 f x 大 于二 x。 好, 第二问, 第二问,就第二问,就稍微复杂一点了。 好,我们来看下第二本啊。 第二问的话,那我们还是算。呃,算一下吧。就 g x 等于什么?等于 f x 的 三 x 加 tangent x 减去 x 平方分之一,是吧? 那我们 x 属于这个区间,我们求个导嘛,导数等于什么?等于扩散 x 的 绝对值,是吧?然后加上这里是扩散平方 x 分 之一嘛?然后这里是加上 x 立方分之 二,是不是这是正的,这也是正的,这也是正的,那大一点说明这个 g x 是 不是单调递增的,是吧? 好,他问你在这个区间上有没有唯一的零点?那我们算下 g k 派嘛,就等于三引 k 派加个绝对值,是不是加 tangent 里 k 派再减去 k 派的平方分之一,这里是零,这里也是零,减去一个数,那肯定小于零,说明 g k 派也小于零,是吧? 那我还要算一下 g k pi 加二分之 pi, 看它大一点还是小一点吧。等于三 in k pi 加二分之 pi 加个绝对值,是吧? 呃,再加上一个 ten 角呢? k pi 不要了, k pi 这个代入就是就是二分子派,是吧?我们知道二分子派是没有添加二分子派是没有意义的,但是你可以把它看成你可以把它看作是正无穷,是不是看作是正无穷,你把也可以把它看成正无穷,是吧?再减去一个 k 派加四分之加二分之派的平方分之一,这个正无穷,这里是个平方,它肯定大于零,是吧?说明这个在这个区间 k 派到二分之派加 k 派上,它肯定有唯一的零点, x k 是 这了吧?啊,这个,这个第三位的这一部分我们就挣到了嘛, 那,那还要挣这个是不是?那,那我就写个同理就可以了,是吧?同理在这个区间, 哪个区间?就 k 加一派到二分之派加上 k 加一派,那是不是也有唯一的零点,也有唯一的零点,是吧?唯一的零点 x k 加一。但是我们是要证这个减,这个小于派啊,我们是要证这个零点减就这两个零点的距离啊,它不会超过派,它是小于派的,是不是?怎么证? 那我们就,呃,我们就,那我们就算一个距 x k 加一 减派就可以,是吧?它是等于什么?等于 sin, 呃,等于 sin x k 加一 它的键嘛?减个派加个绝对值,是不是再减去,再加上它这里 x k 加一,再减个派,再减去 x k 加一减派的 平方分之一,好,这个 pi 就 不要了,就就除以 x k 加一的绝对值,是吧?这个 pi 也不要再加上它的绝对 x k 加一嘛,是吧?再减去 x k 加一减 pi 的 平方分之一嘛,而这个 它就等于什么?根据 x k 加一是个零点嘛,它就等于 x k 加一的平方分之一,是吧?减去 x k 加一减派的平方分之一,这个分母要大嘛?这个减了一个分母要小嘛,所以它是小于零的,是不是说明 g 它是小于零的, 而零是谁啊? 而零是 就是 x k 加一减派,所以 x 加一减减派,它是在哪个区间上?它是在这个区间上,是吧?而这个零可以写成 g x k 嘛, 是吧?然后把这个 g 去掉嘛,说明 x k 加一减派要小于 x k 嘛?说明 x k 加一减去 x k, 它是不是小于派就得正了?所以第二位我们就正出来了,是吧?第二位我们就正出来了。那再看第 第三问,就第三问。好,我,我请个朋友也来讲一下吧。好,第三问,第三问。二的话,在二的条件下,我们证明这个四个码就 y 一 加 y 二,一直加到 y k, 是吧?我们挣它小于派方分之一嘛。好,我们来看一下 y k, 它说了是等于 x k 减 k 派,是吧?那我们根据 根据第一问嘛。我们它是二 x, 我 们乘一个二,两边乘一个二,好吧,我们两边乘一个二,就两倍的 y k, 它就会等于两倍的 x k 减去 k 派, 是这样的吧?然后根据这个 s k 减去一个 k 派,它会小于什么? 这个 x 两倍的 x k 减去 k 派,它就会小于什么?根据第一问的结论,二,二 x 是 小于 sin x 的 绝对值,加 tangent x 吧。所以两倍的它把它带到这里来,它就会小于。呃, sin x k 减 k 派,是吧?再加上一个绝对值,再加上一个 tangent x k 减 k 派嘛? 好,这 k 派我们不要了,它就会等于什么?这个它就会等于 sine x k 的 绝对值,是吧?再加上 tangent x k, 是 这样的吧? 好,它会等于这个。 那这个呢? 我们根据第二问的结论这个东西啊, 根据第二问的结论,这个东西在第二问的条件下,是吧?根据第二这个东西等于什么? 这个东西就会等于 s, 因为这个相减等于零,是零点吗?是这个这个 x k 吗?是这个函数零点,是吧?说明这个这个就会等于 x k 的 平方分之一是不等于它,然后 s k 呢? s k 我 们知道它是大于 k pi 小 于二分之 pi 加 k pi 的,是吧?我们要知道它是大于 k pi 小 于二分之 pi 的 平方分之一, 所以我们要证的这个二 y k 它就会小于小于。这里展开来就是展开来就是 k 的 平方乘以 pi 的 平方分之一嘛,是吧?提一个 pi 的 平方分之一出来就是 k 方分之一嘛, 然后我们再来放缩,它是小于什么的? pad 平方分之一乘上 k 分, 乘上一个 k 分 之一,减去一个 k 加一分之一嘛?对,把它放 啊,把它放小放小,对吧?这 k 减一啊,这个 k 就 这样的小于它,然后我们把它算一下啊,就两倍的 y 一 加两倍的 y, 二一直加,加,加到两倍的 y k 它就小于。什么呢? y 一 就不要动了, y 一 就是 y, 一 就是两倍的 y 一 就是 把一带进去,这个就两边的 y 不要放缩,它就是派方分之一,是派方分之一啊,一不要缩,然后从第二项开始放缩,呃,再加上一个, 再加上一个。嗯, 呃,从二第二项开始放出来,就是加上一个派方分之一,然后二的话带进去, 把二带去一分之一,减去二分之一,是吧?然后第二项把二把三带第三项把三就二分之一减去三分之一嘛?一直加加到一个 k, 减一分之一,减成 k 分 之一,是吧?然后这里都底下了嘛, 就剩下一个什么派方分之一加派方分之一,就派方分之二减去一个, 呃, k 分 之一乘到派分之一,那肯定要小于派方分之二,这是两倍的,是不是?那把二除过去是一个嘛? k 等于一到 nyk, 把二除过去嘛,就会小于派方。分之一就挣到了啊。所以这个第三问要用到放缩,这个放缩就很难想得到。好,我就讲到这里。
32高中数学风清扬
猜你喜欢
- 2314PG物理
