圆柱和圆锥的立体图怎么做
粉丝278.1万获赞1403.3万
相关视频
 01:40查看AI文稿AI文稿
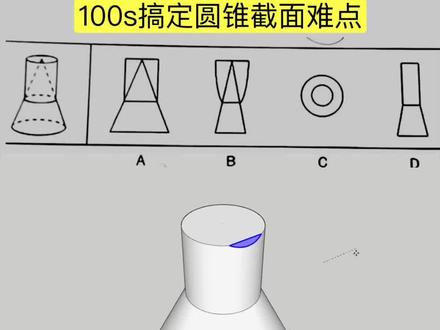
01:40查看AI文稿AI文稿我要是出题人,这洁面不是手到擒来吗?双椭圆叠加洁面首先感谢这位同学的提问,这是一道非常好的例题,下方是一个圆锥,上方是一个圆柱,它们重叠的部分呢,是掏空的。我们先看简单的洁面 c 选项,直接横切上半部分就行了,同心圆。 其次比较简单的 a 选项,直接竖着切,切到最中间就行了,竖切圆柱上方是矩形,并且过了圆锥的顶点,竖切他是三角形,所以 a 选项是正确的。然后昨天这位同学说选二 b, 大家看我沿着顶点这个水平线为轴去转动的时候,我得到的就是三角形。 这就暴露出来一个问题,大家还是对圆锥圆台不是那么的熟悉,老师之前总结的基础界面里面,斜切圆锥顶点,他得到的是三角形。 这道题,这个洁面把圆柱、圆锥难点全部囊括了,非常值得我们结合起来学习。我把洁面斜切的角度压大一点,我们来看一下现在这个洁面。首先斜切完整的圆柱侧面,我们看这两个椭圆不是同心的斜切圆锥得到的,椭圆会靠下一点 洁面继续往下走,大家仔细观察它的变化。当洁面横穿圆柱下底直径的时候,我们看上半部分椭圆是斜切圆柱得到的,下半部分椭圆加上中间的那个空心的椭圆,组成一个完整的椭圆,这个椭圆是斜切完整的圆锥侧面得到的。 虽然讲的这个洁面和我们的体里面没有任何关系,但是这是非常重要的要点,洁面角度继续压大,我们可以看到刚才讲的更为明显, 此时洁面穿过单独的下方圆台,洁面继续往上提,我们看这两个椭圆并不是同心的,内部的会靠下,因为是斜切圆锥得到的。老师反复强调的东西大家要熟记,上了考场直接做个秒选。
3264公考志远(立体图推数资分享) 02:12查看AI文稿AI文稿
02:12查看AI文稿AI文稿圆柱和圆锥垂直相贯,切换到左视图看投影形状。左视图圆柱与圆锥相切,切换到主视图看投影形状。相贯线积聚成两相交直线。第一步,找四个特殊点,在左视图标出四个特殊点。 主视图圆柱与圆锥的交点就是一点和三点。长队正在俯视图,找到一点和三点, 取两点和四点所在截屏面处的结交线半径,画圆弧, 延长圆柱轮廓线与圆弧交点就是两点和四点。 第二步,找四个一般点,找到圆柱与圆锥的切点,过切点做辅助线,并在主视图找到一点,标上五点和六点。 主视图相贯线积聚成两相交直线,连接得到两相交直线。取五点六点处的圆锥半径,再俯视图画圆弧, 圆弧与中心线交点就是五点和六点,做四十五度辅助线。辅助线与圆弧的交点处标上七点和八点。 取七点和八点处圆锥的半径,再俯视图画圆弧,取七点和八点的宽度尺寸平移,过点做辅助线,辅助线与圆弧交点就是七点和八点。 第三步,用光滑曲线连接各点,两点和四点右侧看得见,画成粗实线。两点和四点左侧看不见,画成虚线。 为了便于大家理解本题不擦辅助线,感谢观看!
91手把手教机械制图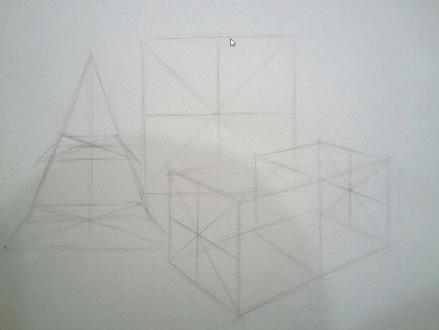 09:33
09:33 02:03查看AI文稿AI文稿
02:03查看AI文稿AI文稿这个视频呢,不讲题,我们再来总结一遍圆柱圆锥的洁面,之前有看过的同学呢,再来复习一次。首先,什么是双曲线?双曲线得是竖着切圆锥或圆台,其他角度的洁面洁得的都是圆锥曲线,就不是双曲线了。当然,双曲线是圆锥曲线的一种, 当洁面经过圆锥的顶点的时候,这个时候两侧变成直线,等腰三角形,圆台呢,就变成了等腰梯形。这里还有一个容易错的点,我把洁面稍微往外拉一点点。 这个时候我们看圆台两侧的它是直线吗?它还是双曲线的一部分,我们可以对比左侧的圆锥去看,大家不要看着它像直线,就以为它是等腰梯形。 ok, 这是双曲线。我们继续看圆锥上方有个小面,对吧?我做的这个小面是平行于圆锥的某一条母线的, 我以这个小面的角度去切割模型,这个时候捷德的曲线它就是抛物线,抛物线也属于圆锥曲线的一种。 当然,这两条线的考点在公考的考场上是不可能会考到的。我们继续往下看。关于圆锥圆台的另一个考点也是难点, 洁面角度继续压大,使得洁面穿过完整的圆柱,圆锥圆台的侧面也就是现在这个样子。我们可以观察到,同底同高的圆柱和圆锥捷德的椭圆洁面是不一样的,圆锥捷德的椭圆会更靠下一点,这个考点被设置成干扰选项,考过不下三次。 好,这是关于椭圆的洁面,我们继续往下看。我记得老师之前讲过,圆柱斜切两侧一定是曲线,可以做到秒选和排除,但是大家不要记混了呀,圆锥和圆台斜切两侧是可以有直线的,这个条件比较特殊。 什么条件呢?就是这个洁面必须经过圆锥的顶点,圆台呢,经过两条母线的延长线交于一点,那还不就是完整圆锥的顶点吗?一个意思啊, 这个时候斜切圆锥所截得等腰三角形,圆台所截得等腰梯形,必须洁面经过顶点。如果不经过顶点,哪怕洁面向上或向下移动了一丁点也不行,他两侧立马会变成曲线。好了,这就是关于圆锥圆台所有重难点考点,大家注意归纳总结。
 03:06查看AI文稿AI文稿
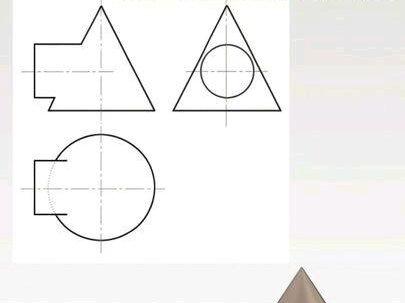
03:06查看AI文稿AI文稿圆柱与圆锥垂直相贯,相贯线是复杂的空间曲线,本题利用取点法作相贯线。第一步,找四个特殊点。 左式图标上四个特殊点。主式图可以直接找到一和四两个特殊点,长对正,找到俯视图一点, 长对正,找到俯视图四点。接下来找二点和三点,取两点和三点所在圆锥处半径在俯视图画圆弧 延长,圆柱轮廓线与圆弧的交点就是两点和三点。 长队正在主视图水平中心线上找到两点和三点。 第二步,做四个一般点,左试图过圆心做圆锥素线的垂线,找到垂足, 垂足所在的高度做水平线与圆的焦点就是两个一般点。标上五点,六点, 取五点和六点所在圆锥处的半径,再俯视图画圆弧, 取五点。六点的宽度尺寸,在俯视图找到两点 平移过点做辅助线,辅助线与圆弧交点就是五点和六点。 高频齐在主视图辅助线上找到五点和六点。五点和六点是主视图相贯线,最右侧点做四十五度,辅助线与圆交于一点, 过点做水平辅助线,交点就是七点和八点。 过七点和八点做截平面辅助线 取结交线半径,在俯视图画圆弧, 取七点。八点的宽度尺寸在俯视图找到两点,过两点做辅助线与圆弧交于两点,两点就是七点和八点。 长队正在主视角辅助线上找到七点和八点。 第三步,用光滑曲线连接各点,得到相关线曲线。 圆柱下方的曲线看不见,画成虚线。 本题为了便于大家理解,辅助线没有擦除,感谢观看!
273手把手教机械制图 03:57查看AI文稿AI文稿
03:57查看AI文稿AI文稿同学们,今天我们来学习人教版小学数学六下第三单元,圆柱与圆锥,圆柱的体积立五。联想到圆的面积计算公式的推导过程,我们把圆柱的底面分成许多相等的扇形,把圆柱切开, 再像这样拼起来,得到一个近似的长方形。分成的上行越多,拼成的立体图形就越接近长方形。这个长方形的底面积 等于圆柱的高,长方形的体积等于底面积层高。长方形的高 和圆柱的高相等,所以圆柱的体积就等于圆柱的底面积乘圆柱的高,这样我们就得到了圆柱体积的计算公式。体积我们通常用大写的 v 来表示, 底面积我们用大写的 s 来表示,高,用小写的 h 表示,所以 v 就 等于 s h。 这里同学们发现了没有,不管是圆柱还是长方体,其实它的公式都是底面积乘高。对于所有的 柱状的几何体,它的体积都是底面积层高,比如说三棱柱,它的体积 v 也是等于 s h。 那 我们知道这圆柱的底面积计算公式是派 r 的 平方,我们把它带进去, 就得到了另一条计算体积的公式 v 等于派二的平方 h。 这样我们就得到了圆柱体积的两条计算公式。已知条件告诉我们哪些信息,我们就用相应的公式计算。 接下来我们来看两个题目,接下来我们看两个练习。一、一根圆柱形木料,底面积为七十五平方厘米,长为九十厘米,他的体积是多少?这道题目告诉了我们底面积是七十五 平方厘米,长为九十厘米。那么同学们思考一下,这里的长指的是什么呢?通过图我们也可以发现,布料的长其实就是圆柱的高,所以这里是高,是九十厘米。那我们根据圆柱的 体积公式, v 等于 s, h 就 等于七十五乘九十等于六千七百五十立方厘米。下来再看一题,挖一口圆柱形水井,地面以下的井深为十米, 底面直径为一米,挖出的图有多少立方米?我们也先来画个图,这是地面往下挖一个圆柱形的井,那挖出的 泥土的体积就是这个井的容积,告诉我们底面直径为一米,井深为十米,这里的井深十米, 也就是这个圆柱的高是十米。同学们一定要注意,有时候远处的高他可能 叫长,也有可能叫深,我们要灵活的去思考。 v 等于派二的平方, h 就 等于三点一四乘,直径是一,所以半径是一除以二,它的平方乘 h 十 三点一四乘,这里是零点五的平方,零点二五乘十二点五就等于七点八五平方米。答,挖出的图有七点八五平方米。这节课我们就上到这里。
17小数轻松学 01:45查看AI文稿AI文稿
01:45查看AI文稿AI文稿这是一款小学生使用的圆柱与圆锥体积演示器,还原课本推导过程,包含了圆柱和长方体之间的转换,等底等高的圆柱。这是一款小学生使用的圆柱与圆锥体积演示器,还原课本推导过程,包含了圆柱和长方体之间的转换,等底等高的圆柱。 圆柱圆锥六合一演示器辅助学习六年级圆柱圆锥单元,学习圆柱的体积还原公式。推导过程立体呈现圆柱与长方体的相互转换,学习面动成体。
 00:54查看AI文稿AI文稿
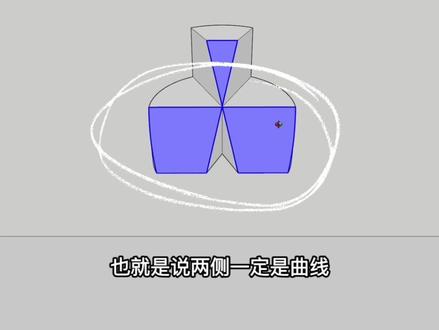
00:54查看AI文稿AI文稿我要是出题人,我会出这样的洁面作为斜切圆柱来考察这道题呢,之前讲过一次,讲的不太好,我们再来看一遍。 首先 c 选项竖着切就行了, c 和四 d 选项很相像,那么四 d 它大概率也是可以的,我们来看,只需要给 c 选项的洁面基础之上旋转一下就行了。我建的这个模型呢,每一层的高度有点高,看的比例不太对,但是它形状是满足的,为什么要做这么高呢?因为我要给二 b 选项做一个更直观的解析, a 选项正是视角竖切,这个没什么好说的。接下来我们看老师开头说的没讲好的就是这个二 b 选项,因为上一次的建模每一层都有点矮了,所以斜切之后看的两侧不像是曲线。来,我们这次再看很明显的两侧的曲线, 斜切圆柱的侧面得到的必定是椭圆或者是椭圆的部分,也就是说两侧一定是曲线。我们看二 b 选项,它下方两侧它是一个竖着的直线,所以直接就选了百分之三十的正确率又何妨呢?多简单呀!









