200新高考一卷立体几何答案
粉丝314.4万获赞2640.1万
相关视频
 05:14查看AI文稿AI文稿
05:14查看AI文稿AI文稿这是刚结束的二零二四年新高考一卷的立体几和解答题,我们一起看一下这道题难不难。首先看一下题目四人追 p a、 b、 c, d 中 p a 垂直于底面 a、 b、 c d, p a 等于 a, c 等于二, b, c 等于一, a, b 等于根。三、 我把条件标在题目上,可以看出角 a、 b、 c 为一个直角。接下来我们看一下第一问。若 a 的垂直与 p b 证明 a 的平行与 p b、 c, 这是 a 的,它是垂直与 p b 的 证明。因为 p、 a 垂直于底面 a、 b、 c, 所以 p a 是垂直于 b、 c 的。 又因为 a、 b 方加上 b, c 方等于 a、 c 方,所以 a、 b 垂直于 b, c, 又因为 p a 交 a, b 等于 a, 那么 b、 c 就垂直于平面 a、 p、 b 同样,我们证明一下 a 的 p a 是垂直于 a 的, p b 也是垂直于 a 的。 p a 交 p b 等于 p 点,所以 a 的垂直于平面 a p、 b 因为 b、 c 也垂直于平面 a、 p、 b 垂直于同一个平面,两条直线平行,所以 b、 c 是平行于 a 的。又因为 b、 c 是属于平面 p、 b、 c, 所以 a 的平行与平面 p、 b、 c。 这是第一问。接下来我们看一下第二问。在题干中的条件下,这里又给出了 a 的垂直与的 c, 这里是一个直角且二面角 a 杠 c、 p 杠灯的正弦值为七分之,根号四十二,求 a 灯。我们先建立坐标系,如图所示,建立 a 杠 x y z 空间坐标系。 我们先过 der 点做 a、 c 的垂线垂足为一。我把三角形 a、 d、 c 的平面图画在下面,过 der 点 做 a、 c 的垂线垂足为一,并设 a 的等于 t。 我们可以从这个平 前面图形看一下,这一个边为 tac 是等于二的,这里又是直角。根据摄影定理, a 的方式等于 ae 乘以 ac 的,所以这里的 t 方等于 ae 乘以二, 所以可以得到 a, e 四等于二分之 t 方。勾固定理可以得到 a, e 四等于根号下 t 方减去四分之一倍 t 的四次方的。所以这时我们就可以找点的坐标 p 点的坐标零零二, c 点的坐标零二零 de 点的坐标 x 是负的,得一长度, y 的坐标是 a 一的长度二分之梯方, z 轴是等于零的, p, c 向量是等于零二负二 二 d c 向量根号下 t 方减去四分之一 t 的四次方,二减去二分之 t 方零,然后射出平面 d、 c, p 的法向量。 根据发销量垂直于 p, c 都是建立方程组 减得法销量 n 一是等于, 同理,我们可以得到平面 p a、 c 的发香量, 四为一零零。因为我们由法销量得到二面角的余弦值,所以我们先根据正弦值算出余弦值。因为三 inset 是等于七分之根号下四十二,这里可以看出这一个二面角为锐角, 所以扩散 inset 等于根号下一减。 say inset 方等于七分之根号七。那接下来我们可以用两个法相量表示它的二面角了。 所以扩散与 c 塔等于 n 一乘以 n 二的数量级,除以 n 一的模和 n 二的模等于七分之根七代入 n 一, n 二项量可化减的 t 的四次方减去七倍 t 方加上十二等于零。可以选择 t 方等于三或者 t 方等于四及 t 等于 根,三或者 t 等于二。但是 a 都是直角边, ac 是斜边等于二,要舍去最终 a 都是等于根三的,这是这一道题目。
1350我是小余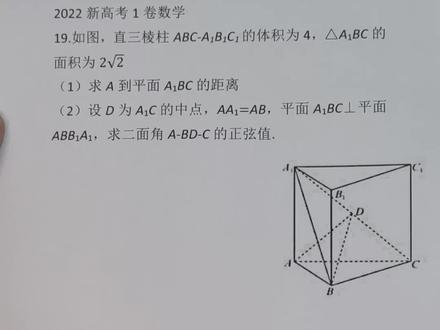 11:48查看AI文稿AI文稿
11:48查看AI文稿AI文稿好,今天咱们讲一下新高考一卷数学的第十九题,说有一个值,三棱柱在这,对吧?他的体积是四,然后他还告诉我,三角形 a 一 b、 c, 他的面积是一个二倍的根号二。然后第一问,让我们求点 a 到平面 a 一 b、 c 的距离, 那么看到这个,他告诉我体积的话,又告诉我这个面的一个面积,我是不是可以考虑用一个等体积法求高的方法,把这个面距离给求出来,对不对?好,所以说第一步我们先把这个大的一个三龙柱的体积表示一下。 好,它的体积是不是等于底面积乘以高啊?最后得到的结果应该是四,对不对?因为题中告诉我了。好,接下来我再把这个三棱锥 a 一 abc, 他的体积也表示出来。好,很明显,我知道三角形 abc 的面积乘以 aa 等于四,那么这个三龙锥的体积我们是不是不是也可以直接表示出来等于三分之一乘以四,等于三分之四, 那么好,这时候我切换一下他的面积表达方式。好,此时我不以这个三角形 abc 为这个三棱锥的底面啊,我考虑用三角形 abc 做这个三棱锥的底面, 那么这时候这个三棱锥的高是不是就是点 a 到平面 abc 的距离?所以说我设一个未知数啊,设 a 到平面 a, e, b、 c 的距离是 d, 好,射出来这个距离以后, 我换一种方式来表达他的体积。好吧,好,我们来看题干中 a、 b、 c 的面积,是不是他已经告诉我了,是不是一个二倍的根号二啊?那么这样的话,我是不是可以通过这个公式把 d 给求出来,对不对?那这样的话我们就知道, 好,这样的话是不是 d 求出来了?也就是说 a 到平面 abc 的距离就求出来了?好,第一问我们就解决了。 好,接下来我们来做一下。第二问,说点 d 呢,是这个 a、 e、 c 的一个终点,然后还告诉我 a、 a 一和 a、 b 长度是一样的,然后他又告诉我这个面 a、 e, b, c 垂直于侧面 a, b, b, e, a 一,然后让我们来求这个二面角 a、 b, d, c 的一个正弦值。 那么想解决这道题的话,我们是不是考虑用间隙的方法来做,对吧?哎,所以说这道题我的这个思路大致是这样的啊,呃,我们首先我们来看 bc 这条线是不是面 a 一 bc 和 abc 的一个交线啊,对不对?而这两个面是不是都都垂直于这个侧面,所以说这个 bc 其实也垂直于这个侧面,对不对?所以说我考虑。哎,先把这个条件写出来,正出来, bc 和 ab 是垂直的。好,那么我来写一下啊, 好,这个 bc 垂直于 ab, 我们已经。呃,正出来了,那接下来我们应该可以这样间隙了。但是还有一个问题,就是这些点的这个坐标我们该怎么表示?因为他们都没 没有告诉我他们具体的长度,所以说这道题需要想办法引入一个量来求出他们个点的坐标,对吧?这时候我考虑怎么样呢?我可以考虑过 a 点向 a、 e、 b 做一条垂线,我们来看看会有什么效果。 好,我们在这做一条垂线,我设这个垂组为 h, 那么我们这就可以写做这个 ah 垂直于 aeb。 好呢,根据题,我们知道这个 a、 b、 c 啊,是和这个 a、 b b 一 a 一这两个面是互相垂直的,那么这个 a、 h 又垂直于他们的交线,那么我们是不是就可以通过这个条件来推出 a h 垂直于面 a e、 b c 啊?所以说我把它写一下, 好,我写出来以后我正出来了, ah 是垂直于平面 abc 的,那么这样的话,我们是不是就知道这个 ah 其实就相当于第一第一位中的这个 d 啊?所以说 ah 的长度是不是有了 啊?所以说 ah 就等于这个 d 呗,等于什么?根号二是吧? 那 a h 的长度有了,我们看还有这个条件没有用,对不对?我们知道这个三角形 a e a b 是一个直角三角形,而且 a e a 等于 a b, 所以说它是一个什么三角形啊? 等腰直角三角形对不对?那对于等腰直角三角形的话,我知道他这个 ah, 他这个斜边上的高的长度,那么是不是他任何一条边的长度我们就都可以求了,对不对啊? 我就可以写啊,因为在这个直角三角形啊,直角三角形这个 a e、 a b 中啊,我们知道这个 a e a 等于 a b, 还有就是 a h 垂直于 a e b, 并且这个 ah 还等于一个根号二,所以我是不是就可以得到 aea 等于 a b 就等于钢号二倍的他,对不对?等于几啊?等于二嘛,对吧?然后这个 a e、 b 这个斜边对不对? a e b 就等于多少?就等于个二倍的钢号二。 好,我们再来看上边,我们是不是推出 bc 垂直于这个平面 abba 呀?就是 bc 垂直于这个侧面, 所以说我是不是可以得到 bc 也垂直于谁啊? aeb 啊,对不对?我可以写,因为这个 bc 啊,是垂直于平面 abba, ae 的,所以我们就知道 bc 是垂直于谁啊?垂直于这个 aeb 的, 那么好呢,在这个直角三角形啊,这个 a 一 bc, 那么我们就可以知道这个三角形 a 一 bc, 他的面积就等于二分之一倍的 a 一 b 乘以 bc, 对不对?等于多少?等于一个题干中告诉我二倍的根号二, 那么 ab 的长度有没有? ab 的长度是不是在这?是不是二倍的更好?二,所以我就可以知道 bc 的长度就等于什么?就等于四倍 的根号二,去除一个 aeb, 然后代数,最后求出来 bc 的长度是几就是二,所以说求出来呢,这么多长度了,那么各个点的坐标我是不是间隙以后就能确定了?好,接下来我们开始间隙啊,因为地方有线,所以说我又换了一张纸, 那么我已经把刚才咱们求的结果,比如说 ab 等于二, bc 等于二,包括他们的这个侧棱 aaebb, ecc 一等于二,他们的长度都已经标出来了, 那么接下来我就可以以 b 为原点,以 bc 为 x 轴,以 ba 为外轴,以 bbe 为 z 轴,我们间隙啊,好,那么这个轴呢?它是一个 x 轴,对不对啊?然后这呢是一个外轴, 好,然后上方这是一个这种画一点歪啊,好,那么我把这个写一下 好,建完戏以后,那么他们各自点的这个坐标,我是不是就可以标一下了?比如说 c 点的坐标,他是不是就是一个二零零啊?然后这个 b 点坐标,当然他是远点了,对不对? 然后这个 a 点坐标,他相当于就是一个零二零,那么这道题这个 b 一点我用不到,对不对?那么我把 a 一点的坐标不要写 a 一点的坐标,呃,是一个零二二, 最后这儿这个地点我也要用到,对不对?题中告诉我,这个地点是一个 a、 e、 c 的终点,那么地点坐标是不是就是 a 一和 c, 他们坐标之何在?除以二啊,对不 对?那么就是他们相对应的坐标之和除以二,其实就是一一一。好,那么他们各自点的坐标我标出来啊,对吧?那接下来呢?我这个设设出这个两个平面的法项量,我们要求的这两个平面的一个法项量。好,我先设 这个平面 abd 啊,这个平面的发现量,好吧,设这个 n 为他的发现量, 同样道理,我设这个 m 项链啊,是另一个面的法项量,对吧?用 x 零 y 零 z 零来表示, 好射出反向内以后,我们把他们给求出来,对吧?呃,首先我们知道这个 n 项量,对不对?他应该是乘以这个 b a 项链等于零,还有一个是 n 项量去乘以一个 b d 项 项链,对吧?应该等于零。那么因为 b 点是原点,所以说 b a 项链和 b d 项链的这个值,其实就是他们的一个坐标的值,对吧?所以说我一乘就可以直接得出结果。呃,得到第一个,首先得到一个二 y 等于零, 对吧?第二个得到一个 x, 加上 y, 再加上一个 z 也等于零,那这样的话,我可以推出啊,得到一个就是 y 等于零,然后 x 等于负 z, 然后我另这个 x 等于一,那么我就可以得到这个 n 项量, 他相当于是一个一零负一,同样道理,这个 m 项链,对吧?他应该乘以谁啊?乘以 b c 项链等于零,对吧?还有一个 m 项链乘以一个 b d 项链也等于零,对吧?那么把数带进去以后, 可以得到,一个是 x 零等于零,另外一个是 x 零,加上 y 零,加上 z 零等于零,这样的话,我就可以得到啊,这个 x 零等于零,然后这边是一个 y 零等于负 z 零, 然后我让这个 y 零等于一,对吧,就可以得到这个 m 项量等于一个零一负一。 好,下一步我们求一下两个法项量夹角的鱼线值,对不对?那么我们求那个正的值吧,所以说就是一个扣赛啊,这样绝对值。这个 m m 项链和这个 n 项链的一个,呃,夹角的鱼线值,他等于什么呢?两个的项链的基对不对? 两个下量的机除以他们的膜啊,除以他们膜的机,对吧?好,然后等于什么呢?哎,我们来看 看一下,一乘零零,一乘零零负,一乘负一就就是一,好,下一边呢?呃,这个,他的这个魔长是不是一个根号二,对吧?呃,这边是一个根号二,然后这边也是一个根号二,所以说他的结果应该等于多少?等于二分之一, 对不对?好,那既然他们夹角的这个鱼线值啊,我们算的那个正值是二分之一,那么他们夹角的这个正线值对不对?我们是不是就得到了?应该等于多少?是不是应该是一个二分之一个号三呀? 好,那么我们知道啊,因为这个法项量啊,他的这个夹角与二面角互补,对不对? 好,所以我就可以知道这个二面角 abd c, 他的一个正弦值也等于多少二分之二十三。好,所以说这道题的结果就是这个。
1297小杨数理化 04:33查看AI文稿AI文稿
04:33查看AI文稿AI文稿二十题的第一问是立体几何的证明?看到交线这两个字呀,就要想到我们学的四大判定,四大性质当中涉及到交线的有什么定理?常考的能用到交线的就两个, 一个是关于平行的,如果直线 m 平行于平面,而法直线 m 又在平面背他内, 那么这个 m 啊,就平行于 r 法与贝塔的交线 l。 符号语言就是 m 平行于 r 法 m, 韩语贝塔,尔法交贝塔等于 l, 能推出 m 平行于 l。 另外一个是面面垂直的,如果尔法垂直于北塔,尔法交贝塔等于交线 l m, 韩语 r 法 m 呢,又垂直于交线 l, 能够推出 m 垂直于贝塔。但是这个定理啊,有一个非常关键的条件叫面面垂直,而这个题目当中并没有给我们面面垂直的条件,所以他肯定考察的是第一个定理。 怎么用呢?先看是哪两个面的交线,平面 p a d 和平面 p b c 的交线为 l, 那么这两个平面肯定就是一个是尔法,一个是北塔,交线是 l。 那还要找到一条直线 m, 证明 m 与一个平面平行。 这个题目的图中啊,底面是个正方形,那么 a d 和 b c 就是平行的, a d 平行于 b c, b c 又是 p b c 这个平面内的一条线,所以 a d 是可以证明出来它平行于这个平 平面 p b c 的,而 a d 呢,又韩语平面 p a d, 所以说 a d 应该平行于 p a d 和 p b c 他们两个的交线。 证明到这里呢,就可以证明 ad 平行于这个交线 l 了。但是要正的是垂直呀,我们要正 l 垂直于平面 pdc 哎, l 和 a d 是平行的,所以只需要证明 a、 d 垂直于平面 p, d, c。 一块写一下步骤,因为正方形 abcd 中 ad 平行于 bcbc, 韩语平面 pbc, ad 不含于平面 pbc, 所以 ad 平行于平面 pbc, 这样就正常 出来线面平行了。接下来我们用线面平行的性质,因为啊, a、 d 韩语平面 p a, d 平面 p a, d 交平面 p, b, c 等于 l, 所以得到 a、 d 平行于 l。 按照我们的思路呀,想证明 l 垂直于平面 pdc, 只需要证 a、 d 垂直于平面 pdc。 要证明线和面的垂直,只需要证明线垂直于这个面内的两条橡胶直线。 因为 p d 垂直于平面 a, b, c, d, a, d 呢?他有韩语底面 a, b, c, d, 所以 p d 垂直于 a, d。 又因为正方形中 a、 d 垂 至于 d, c, 这样就有两个垂直了,还需要写一个香蕉 p, d 交 d, c 等于 d, 所以说 a、 d 就垂直于平面 p, d, c。 前面证明了 ad 平面 l, 现在又证明了 ad 垂直于平面 pdc, 所以我们就可以得到 l 垂直于平面 pdc。 看一下评分标准啊,写出来 a、 d 平行 b, c 一分,证明出 a、 d 平行 p b, c。 线面平行得一分,累计两分。 如果这里的韩语和不韩语都没写这一份,扣掉证明出来 ad 平行 l 得一分,累计三分。如果没有写面面相交于一条交线,扣掉这一份,证明出 pd 垂直于 ad 的一份,累计四分。这里的这个韩语不写不扣分,证明除 ad 垂直于平面 pdc 得一分,累计五分。 但是如果没写 ad 垂锥 dc 或者是这个香蕉这两个哪个不写,都扣掉这一份。最后结论一份的六份,如果前面的证明都不沾边,直接下个结论,不给分。
681袁来有数(高中数学)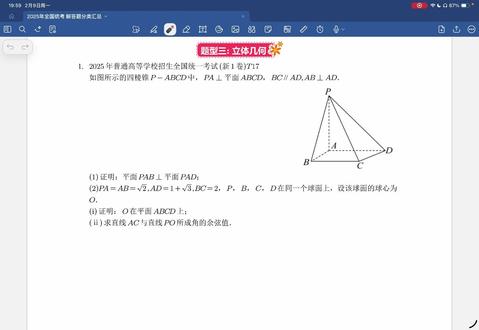 12:53查看AI文稿AI文稿
12:53查看AI文稿AI文稿ok, 今天来看二五年全国统考的解答题分类汇总的题型,三例题即可。第一道题是咱今年的二五年的高考真题一卷的十七题。看题如图,在三棱锥 a、 b、 c、 d 中,四棱锥的 p a 垂直底面。好,这一根线垂直底面 bc 平行 a、 d, 也就是 bc 是 平行 a、 d 的, ab 是 垂直 a、 d 的。 这还有个直角来看题,让我证明面面平行,证明面面平行,需要线面平行 来看题,他让我证明平面 p a、 d, 也就是说这个面和 p a d 和,和这个面和后面这个面是平行的,垂直的。那怎么办?一定要先找线面垂直来,咱先写第一问,正因为题目给了 p a 是 垂直底面的,那这个 p a 好 像就垂直它,对不对?因为它在底面,又因为题目确定给了我这个 a、 b 是 垂直 a、 d 的, 所以我这个 b a 又垂直于 p a, 这个 b a 又垂直于 a、 d, 所以 b a 垂直后边那个面,又因为 a、 b 属于我隔壁这个面,所以两个面相互垂直。这是大致思路,思路有了就可以写了。 但又提之,因为 p a 垂直平面 a、 b、 c、 d, 那 a、 b 那 属于平面 a、 b、 c、 d, 所以 p a 就垂直于 a、 b, 那 又因为题目告诉我了这个 a、 b 垂直 a、 d 的, 那这个 a、 b 垂直 a、 d, 你 这个 pa 还交 a d 等于点 a, 那 pa 和 a d 我 还属于哪个平面属于平面 p a、 d 就是 咱们都属于这个灰色的面,所以这五个条件你就可以推出来。我这个 a、 b 是 垂直于平面 p a、 d 的, 线面垂直,又因为这个 a、 b 是 属于哪个面属于平面 p a、 b 的, 所以你就挣出来了。那平面 p a, b 垂直于平面, p a d。 好, 这是第一本来看第二本,现在告诉我长度了。那 p a 等于 ab 等于根号二,这,这是根号二,这是根号二。 ad 等于一加根号三, ad 等于。哦,这长是一加根号三。这个数有点奇怪。 bc 等于二, 他说 p b、 c、 d 在 同一个球面上,球心为 o。 哎,球,球心是 o, 第一面让我证明点 o 在 平面上,他让我证明点 o 在 里面。这个面的球心有什么特点? 意思是球心到这四个点的距离应该是一样的?换个颜色,我把图中标起来。那屁在这里, b 在 这里, c 在 这里, d 在 这里。球心得到这四个点的距离一样,因为都是我的半径,他让我这么点 o 在 平面 abcd 上,你观察这三个点还正好都在这个平面上, 对不对?那它就能够成一个三角形,那这个球心对于这个底面三角形相当于相当于它的外心。 啥是外心?那啥是外心?有人说啥是不是外心?三角形的外心是三角形的外接圆的圆心。那外接圆心怎么找?你想想,外接圆的圆心到这三个点的距离是不一样,那就是三个中垂线的焦点,就叫做我的外心。 ok, 三个 写这三个中垂线的焦点就是外心,外心外接圆的圆心。 alright, ok, 那 思路有了就可以找了。那我们把底面看做一个三角形,我找到底面的这个 圆心,现在不叫球心的,因为我只关心这个底面,我找到这个圆心,假如找到了,不知道在哪了,反正假如在这了,只要证明在底面上呢?我求出来之后,它已经是到 o、 b、 o、 c、 o、 d 距离相等了,你再去验证一下,你这个 o 到不到点 p 的 距离相等, 如果到 p 的 距离也相等,你就满足这个条件了,他们确实在一个球面上,你就把这个点 o 给求出来。好,那现在咱们写,我们是不是把底面 abcd 看作一个 平面的?现在不在立体几何里面看做平面了,我们在这进行解析,这是 x 轴,这是 y 轴,我们相对于点进行解析,那 b 是 就差不多这么长。 ab, 这个 ab 有 长度没? 看看, ab 没给我长度,那给我 ad 的 长度, ad 差不多在这给我 ad 的 长度吧,这是 x, 这是 y, 还给我 bc 的 长度,那这是差不多,这是二二,比 这短一点,这里就是 c, 这里就是 d。 好, 为啥我画 c 画这不画这?因为 a、 d 是 一加根号三,根号三约等于一点七,那一点七再加一等于二点七,二点七比这个二长,所以 a、 d 在 它右边一点。我们要的是哪三个点?我标蓝 这个点,这个点和这个点,它找三角形的外接圆的外心 外星。刚开始咱说怎么找?就是垂直平分线的交界,那这个垂直平分线嘚嘚嘚嘚,那这条垂直平分线嘚嘚嘚嘚。只要两条线球来,他们一定有个焦点,这个焦点假设为 o, 以球来焦点,等会再验证一下这个 o 到 p 的 距离跟他们距离是不是一样的, 那就能证明他确实是我的球心呢?好,那如果说一平面间隙,我这个点 a 就是 圆心,那我就设 a, a 是 零到零点, b 点 b, 我 看看 ab 多长。 ab 等于根号二,这是根号二,所以 b 点坐标等于根号二到零, c 点坐标是根号二到 c 点 c 在 这里, x 轴走根号二,这是 b, c 等于二啊,所以这就是二,所以根号二到二,那 d 点 d 点在这里, d 点 x 是 零,这是一加根号三, 这是零到一加根号三。好,现在把它当做平面了。平面如何求线的方程?这个这里就是直角,这就是直角了。 垂直是垂直,平分是平分两个条件,现在垂直又平分,所以我这条绿线应该过 bc 的 终点,对不对?好,那我设 bc 终点,比如说 a、 b, c、 d 设为 e 吧。设 e 为 a, d 终点, e 为 bc 终点,那 e 点坐标是几?用?终点坐标等于它加它除以二,那还是根号,它加它除以二是 e。 好, 那是垂直。那这根线的方程如何表示?这里是 x 轴,这里是 y 轴,它的 y 是 不变的,它的 y 不 变,那就是肯定方程等于什么东西?这个点的 y 值你求出来是一,所以这根线的方程就是 y 等于一, 所以你求出来一个直线,直线 l e 方程是 y 等于一,来,你求这个直线 l 二的 l 二就这个方程。那我是不是也需要 c 跟 d 的 中点来设 c, d 中点就 abcdf 吧。 f 为 c, d 中点,那 f 是 多少嘞? c 在 这里, d 在 这里,那相加除以二, 根号二加零除以二是二分之根号二,二分之根号二。逗号外至二加上一倍根号三,再除以二,那就是二分之三加根号三。那 kcd 呢?你垂直平分,这根线与它的斜率之间应该是负一,那 kcd 怎么求? 那就是坐标型减相除喽。 c 在 这里, d 在 这里,它减它分母是根号二, 分子等于二减去一减根号三,等于一减根号三。所以我 k l 二的斜率呢?应该是几?是不是相乘是负一?首先分母倒过来,再填负号等于根号三,减一分之根号二。所以 我就知道了。那直线 l 二的斜率呢?减二方程了,用点斜式方程, y 减去二分之三加根号三, y 减外零等于 k 倍的 x 减去二分之根号二。咱们两个方程,一个是这个是 y 等于一,一个是我刚刚求出来这个方程,两个之间交一点进行连力,刚刚那个方程是 y 等于一内,所以另用这个方程, y 等于另外的一,求出来 x 等于几。 剩下是在草稿纸上写的,答卷卡上直接写另外的一解,得 x 等于几就够了。验算过程不要写它 卡上好, y 点一, y 点一完比赛。那就是一减去。我先抄一遍,一减去二分之三加根号三 等于根号三减一根号二, x 减去二分之根号。好,现在算 x 等于几。来,这里先变成通分加等于二分之二减二减三减高三等于负一减高三,负一减高三。这个我就擦掉,这个玩意要乘过来,那等于根号二的根号三减一。 这里又干掉了。这里你看我把这个符号扔前面去这里变加号没问题吧?那这里发现分母啊,分子,分子可以用平方差公式,等于根号三加一乘根号三减 a 一 方减 b 方等于三减一,是二对不对?所以上面变成二,二跟二约 等于负的根号二分之一,那你就得出来了,那左边是负的根号二分之一,等于右边 x 减去二分之根号二,那你发现啥?所以这个 x 应该等于零,是不是把它分解一下,它也是负的二分之根号,所以它肯定等于零,解得 x 等于零, x 零,所以你就找到了三角形,你就可以说三角形 b、 c、 d 的 外心起个名字吧,比如说是 o 片。 英语不能起 o 啊,题目告诉你有 o 了,你换个名字起个 o 片呗。记零都一。现在你要验证一下它到点 p 的 距离跟它们的距离是不是一样的。 你先看底面距离,你点 o 是 零到一,那你 r 觉得这个点是零到一,这里是一加根号三是一,这里是一加根号三,所以你的 r 是 不是等于根号三?你可以写三角形 b、 c、 d 外接圆半径小二等于根号三。 你是不是要验证一下我底面的外角圆跟不跟我这个球是一样的?现在转化成立即三维几何坐标的圆,那我外心坐标也可以写的出来。 o 片片,那就变成了零都一,零都一都零,因为这都是零。 p 点坐标是几啊? p p p p p 在 哪了?我看 p a 是 根号二,那所以 p 点就是零都零都根号二, p 点是零的 o, 零的根号二。验证一下 o 片片 p 的 值等于几?等于根号下作为标相减零减零一,减零是一,加上二,是不是也是根号三,等于二? 经验证,所以这个点 o 就是 我的球心,所以你就可以说球心 o 的 坐标了。因为是在立即集合,所以你要给它改成把这个改成三位的,就零斗一斗,那也就是说在我的平面,所以说这个点 o 在 平面 a、 b、 c、 d 上。 好,这第二位,那第三位,求这两条线的夹角的一线值。首先你看见求两条线一定要有个脑子,两条,三个角,四角, 两条线的夹角永远是选小的这个角,所以这个余弦值一定是大于零的,所以你等会算的时候一定要带上绝对值。明白,好,那求他们坐标 a, 我 写这里,标上 标上一,我把这个一拖到下面去,把这个缩小一下,放到这里泡。现在咱们写第二个, 第二个就更简单了, a 点坐标多少? a 点坐标就是零零零 c 点 c 点 c 点, 根号二逗二逗零。看这里,你 c 点刚刚用平面来写的,你只要把它的 z 轴零表示出来就行了。那 p 点 p 点是 零逗零逗 p a 多高?根号二零逗零逗根号,那球心呢? o 呢? o 你 第二问求了,零幺零零逗幺逗零。好,没地方了,我给他写成横着的形式, all right。 这几周了,无所谓了, a c 相样,把它转换成相样。 a c 相样怎么写? 后减前就是根号二得二得零。好,那 p o 向量呢?等于 o 减 p 是 零到一到负根号二 设,你要设设直线 a c 与直线 p o 所乘角为 c 大, 所以口径 c 大。 带上绝对值,等于 再导上面 a c 向量内积 p o 向量去上它们各自的某长。 right, 然后往里代值等于用眼睛看,根号二乘它是零,二乘一是一,二乘二是二啊,平乘它是零,所以上面正好就是二, 即使算了是算是正的,你最好养成习惯,你要带成带上这个绝对值继续算分是 a c 的 魔, a c 的 魔, a c 在 这里,那就根号加二加四,再乘上根号加 p o 的 魔, p o 在 这里,一加二,快点一下等解,这是六, 这里是根号六,这是根号三。那这个根号六可以分我写这里看我的思路,这边是根号六,这是根号三乘根号二, 对不对?这个根号三跟这个根号三一抵消,就变成了一个三,这个根号二跟上面一抵消,上面就变成了根号三,就等于三分之根号二。学一下,我画点思路,三分之根号,那这题就 over 了。所以你要写卷,所以直线就是抄遍题目,直线 a c 与 直线 b o 错成角,余线至为三个就更好。 nice, 好, 这道题就讲完了,如果不会了,你再往下面丢点,关注老师一下,老师带你飞。数学考一百二十五,很轻松。 let's go! 再见!下节课见!
 12:12查看AI文稿AI文稿
12:12查看AI文稿AI文稿我们来讲解一下二零二三年新高考数学全国一卷立体几何这道大题。立体几何考了这么多年,每年都是间隙设点,毫无新意。在一个四轮座,其实就是说底面呢,是一个正方形,那么它的边长呢?是二, 然后他的侧棱长是四。好,有这两个条件,我们可以直接间隙设点,建立如图所示的坐标系,对吧? x、 y、 z 这三个方向。然后呢,又告诉一些边长, 好,他,他和他,而这三个长度呢,方便我们去描述点的坐标。其中啊,这一段他的长度是一个一,然后呢,这个这个的长度是二,等于这段长度 也是二。好,还有一个长度是这个, ok, 那么这个长度是三啊。大家想一下,有了他,他和他,那么其中这个点,这个点,这个点和这个点,他们的坐标是不是直接可以写出来了? 好,根据我们建立的坐标系啊,我们把第一问用到的这些点的坐标全部给他描述出来。好,首先 b 二是零二二,其次 c 二是零零三。再来啊, a 二是二二幺 d 二二零二,这一步不要出错,这一步出错就全完了,后边都不用做了啊。好,接下来我们把这两项量算一下, b 二、 c 二这个项量,他等 于 c 二的坐标减去 b 二的坐标零负二一。好,同样的道理,我们再来算一下, a 二、 d 二这个项量也是零负而已,那么这两个项量是平行的, 所以呢,我们就直接证明出来了, b 二和 c 二,他们在和直线的是互相平行的。好,这是第一问,第二问呢,难度不大,但是计算量非常大,当然这个计算不要笨,算他也是有技巧的。 a, 那么接下来呢,我们来做一下这个第二问号,看一下第二问,首先注意题目,他说的是哪个二面角呢? p a 二 c 二 d 二好,是这个二面角,那么他涉及到一个新 的点,这个点呢,在 bb 一上面运动,所以我们可以直接把这个点的坐标给他设出来。好,假设点 p 的坐标就是一个零二 b, 因为这个是未知的,所以他就可以在 bb 一上面去运动了。 好,然后呢,我们要去求这个二明角,就要去求把项链,求法项链,看一下需要用到哪些项链 好,通过二面角找我需要的项料有两个平面啊,那么在第一个平面当中,我们可能会用到 c 二 a 二项料, 还会用到 c 二 p 香料好至第一个平面,那么第二个平面也是同 通过二面角,直接通过这些角标去找,可能会用到项料, c 二 a 二项料啊,以及 c 二,他这个项料和这个项料。 c 二 d 二项料。好,刚才那个可能会用到这个项料和这个项料。 那么接下来呢,我们电梯的坐标知道了,那么通过第一问呢,我们已经把 c 二、 d 二、 a 二这三个点的坐标啊,这是 c 二、 d 二、 a 二,他们的坐标全部都写出来了。 好,那么这样的话,我们就可以直接把这三个项链与它表示出来。好,我们来表示一下,首先 c 二 a 二项料,它等于 二二负二,好,再来 c 二 d 二项量,他等于二零负一, ok, 继续 c 二 p 项量啊,他等于零二 b 减三, ok, 接下来我们来表示一下法项量,假设第一个平面 a 二 c 二 d 二,那他的法项量如果是一个 m 项量是 x one z 法向量有一个很重要的性质,法向量是垂直于平面内的任何一条直线,那么它就垂直于我们用平面内的点表示的向量,所以我们就可以得到 m 向量, 点乘上 c 二 a 二项量,这个值是等于零的, m 项量再点乘上 c 二 d 二项量,这个也是等于零的。然后呢,就是项量之间的坐标,用算把他们给他算一下,就可以 得到二 x 加上二 y 减去二 y 等于零,好,其次,二 x 减去 y 等于零,好,根据这个和这个 三个未知数只有两个方程啊,那其实是算不出来的,但是我们可以复直去表示他们之间的一个关系。 好比如说第二式子得到二 x 等于 z 啊,那我其实可以假设 x 的于一,那么 z 就是等于二,再把它们带到第一个式子里边,算出 y 等于一,所以 m 项量等于一。一二, 好,同样的道理啊,同样的道理,我们假设呢?第二个的平面 a 二 p c 二,那么它的法项量 假设是一个 n 项量啊,我们用完全相同的做法,那其实 n 项量他是点乘上我的 c 二 a 二项量是等于零的。其次, n 项量在点乘上 c 二 p 项量也是等于零的,对吧?好,这个具体我们就 不写了,直接给大家。结论。 m n 项量呢,是等于一个二除以三减 b 减一,一,再来一个二除以三减 b。 好,两个项量,两个法项量,确切 的说都求出来了。接下来呢,根据二面角,那么题目呢?看一下题,题目说这个二面角的大小是一百五十度,对吧?好,我们能不能把这个 b 给他求出来了?当然是可以的,在这里呢,涉及到一个简单的几何知识啊, 那么现在我们知道这两个平面夹角呢,是一个冻脚,对吧?一百五十度,好,这是他的发现料,这是他的发现料,这垂直,这垂直,这一百五十度,那么他们的夹角的和这个一百五十是互补的,那么这个角应该是一个三十度。 好,也就说两个限量的假酒使三十度,那么他们的余弦值两个法向量,他们的余弦值应该是一个三十度的余弦值,就是二分之根号三。好,那道理是比较简单 的,这个项链点上这个项链,除以他的膜乘以他的膜,好,那么他这个结果就是一个刚才我们说的,哎,三十度的余先值二分之多少三, ok, 这是算式啊,接下来主要是计算。呃,那么用算量还是比较大的,首先 m 项量点上 n 项量, 用它去乘以它啊,横坐标,纵坐标,竖坐标分别相乘,再相加,你就得到了 二除以三减 b 减一加上一个一,再加上四除以三减 b。 好,这是向量的点乘。然后呢,再除以他们各自的模长, m 向量模长使根号六,然后再乘以这个啊,这个其实如果 通风的话,我们会发现分母都是三减 b, 对吧?好,刚好下,每一个都给他平小方。好,这一呢,我们简单了合并一下, 三减 b 分之二减三加 b, 那就是三减 b 分之 b 减一,对吧?好,他呢就是三减 b 分之 b 减一括号的平方加上一的平方,再加上二的平方除以三减 b 括号的平方。好,这个结果等于根号三比二, 注意到这个地方不要死算啊,看看有没有可以化解的地方,比如说加一减一是不是没有了?好,然后分母同为三解 b, 三解 b 分之六,那么下边这个,下边这个,我如果我们再多写一步啊,这是六除以三解 b, 对吧?然后呢,除以这边是根号六, 六乘以好,他根号下,这是平方,我们把分母全部通分,我们发现这是一个三角 b 的平方,如果给他开根,那开出来就是一个三角 b, 好,接地方,不用担心符号的问题啊,因为呢,我们已经推出来了这两个像量的夹角,一定是他的余弦值,一定是正的,是大于零的,而分母是大于零的,所以分子肯定大于零和三节臂就是大于零的, 那这样的话就可以大大解化我的运算。那开出来这分母是一个三解 b 这分子了,是一个 b 减一的平方,再加上,注意,这是一啊一的话,是不是三解 b 的平方,分之三解 b 的平方,所以这地方特别容易 错,注意,这不是一,这是三角 b 的平方, ok, 然后呢,再加上一个四啊,那么他输等于根号三比二, 然后注意三节臂和三节臂约掉根号六,除以根号六,剩一个根号六,根号六和根号三越下剩余根号二,然后左右两边同时给他平方 平方之后这根花儿变成了二,二变成了四,给他交叉相乘好,这是二,这是四,二,四得八,我们就得到了八,等于他的平方哦,乘以一个一, 他的平方就是 b 方减二, b 加一,再加上九减六, b 加上一个 b 方加上一个四,好,合并一下,这边是二, b 方减去一个八, b 这边是加十加八约一个,剩高二加串六等于零,就得到了 b 方减四, b 加三等于零。好,那这样因式分解, b 减一乘以 b 减三等于零,我们得到 b 有两个值,第第一个答案是一,第二个答案是三。 好,必算出来。注意看下题,题要我们求什么题?让我们求的是 brp brp 的长度,对吧?那 brp 怎么来求呢?注意, br 到 b 的距离是不是二,而我现在 p 啊,我们算出来了,小 b 是等于一或者三的。好,那小 p 的位置呢?在哪里?它的位置一个是倒点 b 的距离是一,一个是倒点 b 的距离是三,这段长度是三。那不管是一还是三,我 b 二 p 的长度 这一段,或者说这一段,要不呢就是三减二等于一,要不就是二减一等于一,不管是一还是三, b 二 p 的长度都是一,所以我们就得到了 b 二 p 长度等于一。 ok, 那么这道题我们就做完了。立体几何这道题思路很简单啊,有一定的计算量,难度呢,不大,只能说是一道比较常规的题目。好,今天分享就到这里,你做对了吗?
1296北京初高中数学李老师 01:51查看AI文稿AI文稿
01:51查看AI文稿AI文稿立体几何怕不怕?大家千万不要怂哦,我们一起来挑战一下。这是二零二五年全国一卷数学试卷当中第九道选择题,也就是多选的第一道。好,请看题目。在正三棱柱 a、 b、 c、 a、 b、 c 中, d 为 b、 c 的 中点,则 a 选项 a、 d 垂直于 a、 c、 b 选项 b、 c 垂直平面 a、 a、 d、 c 选项 a、 d 平行于 a、 b、 d 选项 c、 c 平行于平面 a、 a、 d。 那么该题目我们可以用到两个方法,一个是传统的立体几何的方法,但是呢,针对考试的话,他别浪费时间,所以我不建议推荐我们。第二个方法是建立空间直角坐标系。首先呢,我们先假设该正三棱柱的底边为二,高为 h, 先选定圆点 d 是 零零零,那这样的话,我们会得到, a 是 根号三零零, a 是 根号三零 c 的 话是零负一 h, b 的 话是零一,零一的话是零一 h。 注意选项,向量 a、 d 的 话等于负,根号三零零 a、 e、 c 的 话等于负,根号三负一负 h, 所以我们会得到向量 a、 d 乘以向量 a、 e、 c 等于负,根号三乘以负,根号三加上零等于三,所以它不等于零,那么这样的话, a、 d 跟 a、 e、 c 就 不可能垂直,所以 a 选项错了。那么对于 b 和 c 来说的话,向量 b、 c 等于零负二,零向量 c、 c 一 的话等于零零 h。 向量 a、 a、 e 等于零零 h。 向量 a、 e 的 话等于负,根号三零零。 首先,我们先假设平面 a、 a、 e、 d 的 反向量为,向量 n 等于 x、 y、 z, 那 么这样的话,通过 b、 c 的 选项,我们会得到向量 a、 a、 e 乘以向量 n 等于 h, j 等于零,向量 a, d 乘以向量 n 等于负根号三 x 等于零,那么这样的话会得到 x 等于 j 等于零,那么再令 y 等于一,因为它是法向量,所以呢,向量 n 等于零一零,那么这样的话会得到 b, c 的 向量会等于零,负二零等于负二向量 n, 那 么这样的话,向量 c c 一 乘以向量 n 等于零, 所以我们会得到 b 和 d 都是正确的。那么对于 c 选项的话,向量 a 的 话等于负,根号三零零。向量 a 一 b 一 等于负,根号三一零,那么这样的话会得到负根号三,除以负根号三,它等于一不等于零。显然 a d 平行于 a, b 一 不成立,所以呢, c 肯定错了,所以最后答案是选择 b 和 d。 好, 我是学科王语说物化生,那么听过亲自老师,如果有问,建议反复观看或私信我。最后,喜欢本期视频的话,请点赞、收藏加关注我,我在福州,福清等你哦!
猜你喜欢
最新视频
- 1163久晨ovo











