2022黄冈中考数学标准答案

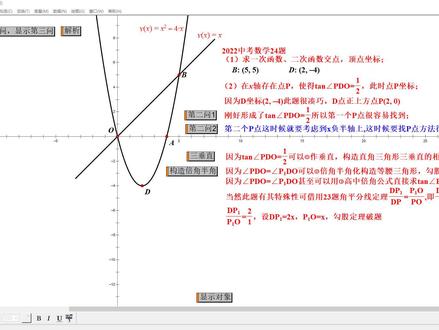
好，各位同学，大家晚上好啊，今天呢，简单的做一下我们今年中考的数学二十四题 啊，关于数学的二十四题呢，他考点呢？还是一个二次函数的几何综合，然后总共有三问，第一问是一个常规题型啊，求一个焦点， 这条一次函数和这个二次函数 y 等于 x 和 y 等于 x 平方减四， x 的焦点啊。第二个求这个二次函数的顶点，顶点，那么这个还是比较好做的，连力求减 以及配方法求顶点式，或者说用对称轴求横坐标，然后带入求中坐标都可以。那么第一问是送分题，第二问呢，我们考察的是什么呢？第二问 是一个稍微开放一点的啊，他这时候是一个运动的点，在 x 轴上存在点 p， 他说一个 p 点在 x 轴上， 然后使得摊进 pdo， pdo 就是 pdo 这个角啊的正切值，它等于二分之一，其实就是求一个定角的问题，对应的点在哪里，而此时点 p 的坐标啊。这题你首先要考虑的 p 点到底会在哪， 是不是 pdo， 有可能，有可能，有可能，是不是在左边这边呢？ pdo 啊，这是右边， xo 正慢走，当然也可以在 xo 的副慢走。 pdo 正确字， 这个正确值。二分之一大概是多少度呢？你可以想啊。呃，贪的三十度等于三分之四，刚好三，这个就比 二分之一要大一点点，所以他应该是二十几度，所以你大概知道他应该是一个瑞桥左右一个瑞桥啊， 那么这一题有些特殊性。为什么说有些特殊性呢？因为第一点坐标啊，这个顶点坐标我们在第一位已经求出来了，他是二负四，如果你机智的去画了这个图啊，你机智去画这个图，你会发现一个问题啊， 当你这个低点往 x 做一个垂线，这个焦点 p 点啊，就会形成了， op 长度是二， pd 长度是 四，刚好是一个直角三角形，正确值就是二分之一，所以这个第一个批点是很容易找到的。那么 x 正正版轴找到了，我们同时要考虑，那第二个批点复古版 的皮点呢？我们该如何去找找副班主的这个皮点啊？说白了就是 odp 这个角的正确值啊， pe 这个角的正确值还是等于二分之一， 他告诉你正确指我们常规的思路呢？常规的思路应该是做一个垂线，因为做垂线我们就可以利用他的正确指得到一个线段之比。当你做垂线了之后，会形成一个什么状态呢？比如说我过欧典往这里做一个垂线，做完垂线了之后， 这里就会形成一个直角三角形，那么直角三角形有什么用呢？我们知道直角三角形啊，他不是等要直角的，他一定可以构造一个三三垂直的相相似。所以这个时候常规的做法，我们会做一个三垂直出来， 比如说做一个垂线，构造三腿直的相似，构造了三腿直相似之后，利用坐标之间的关系啊，他之笔，因为这个斜边和斜边之笔啊，当然在这个大直角三角形里面，我们认为是直角边和直角边之笔是一个正确的一比二， 所以到这两个小三角形上面这个小三角形和下面这个小的直角三角形，他的比例啊，这个相似比也是一比二，从而我们可以利用设为的数啊对应去求解，也可以勾到黄灯去求解，这是一个常规思路， 那这个思路稍微显得复杂一点啊，复杂一点，好，这里我就只说一下思路，那么有了这两个角， pdo 和 pedo 这两个角，因为我们知道这个角和这个角是相等的啊，相等的， 因为我们做出来嘛，右边一个角，左边一个角相等的，他们正确值才相等，所以这个时候我们会想到什么呢？这是一个二倍角的关系，我们可以通过背角和绊角之间的转化的思路来做这一题，那么这个时候我们就会有第二种思路啊，第二种思路 啊，构造一个等腰三角形。等腰三角形这两个两个角是不是两个角，那么就转化成这两个角相等的角，然后这个角啊跟这个角是相等的，正确值也是二分之一。 因为脚相等正确之相的，所以对应得到 pep 这个边，比上 pa 这个边，他也是一个一比二的关系。既然是一比二的关系，我可以通过社会之处，比如说我是 op， op 一我也 x， 因为这里是 二，这里是四，是吧？这这个 p 一 p 一，这个边是二加 x， 那么代表着 p 一 a 二就是四加二 x 既然是四加二 x， 那代表着下面的 呃， dl 呢？就是二， xdl 是二 s， 那么 dp 一的也是二 x， 这里我们就出现一个直角三角形，直角三角形就可以利用什么定理呢？ 勾股定理啊，勾股定理啊，勾股定理，勾到等腰三角形，利用勾股定理去把这个题目做出来，那么求出线段长度对应的皮衣，这个坐标就很好求了，是吧？好，这是第二种事。 第二种思路呢，他实际上告诉我们的啊，这里有被角的关系，是不是 被角和绊脚的关系，所以我们又会想到一个什么呢？呃，如果有大家学了一些，有同学部分同学学到高中的被角公式，他可以直接把这个 pdpe 啊这个正确纸给求出来。 那利用一个背景公司啊，这里就不做拓展，如果知道的，其实也是可以做的啊。好，嗯，其实最特殊的并不是这个地方最特殊，是吧？此题有些特殊性， 为什么特殊呢？因为我们倒数第二题那个几何综合那一题呢？他考察的是什么呢？考察是一个三角形的角平分线的问题， 而这个搅平片是有一个搅平片定理，其实是通过相似推倒的。而在这里，我因为我们知道我们做出来的两个角刚好相耐，这相当于出现一个搅平分线，所以我们可以利用搅平 天地里第一 p 一比第一 p 等于 p 一 o b o p 这个关系，而同儿往里面去，带得到这个第一 p 一，第一 p 一和 o p p 一之比是二比一，还是一样的思维之术 啊，就像前面一样，我们知道这里是 x， 这里是 rx 啊，那么购物定理就可以破提了啊， 这实际上是利用上一文的思路啊，这张试卷里面有三题可以利用那个搅平片定理去做题啊，哪三题呢？一个是铁木泥的最后一题， 他就是一个搅平面定理，当然用确定三角形做垂线也可以做，也可以做啊。我们的倒数第二题，他纯粹就是搅平面定理，我们的最后一题的第二纹也可以用的搅平面定理去做。 思路一样，如果你的填空题的最后一题会做的话，那么这一题你做起来轻轻松松。好，这就是我们的第二问。呃，具体答案我就不解，不解出来了，那么接下来是我们第三问，第二问，他们考察的内容呢？ 实际上是将我们的二次函数跟到我们的三角函数进行一个小结合，是吧？用到了一点点三角函数的知识，然后去破题啊。那么第三问， 第三问是什么样的？第三问，他是存在一点扣点 q， 点 q 啊，这个点 q 是在这个 odb 这个弧线段上运动， 运动的过程中，我们连接这个 mq， 这个 m 点是什么来的？是 b 点，关于对称的对称点 到一个 m 点，是吧？连接 qm 一连之后与依次函数交于一点，那么这个焦点一形成，就会形成两个三角形，上面一个三角形和下面一个三角形，他问你的是这两个三角形， 就是下面这个三角形 b q 与上面这个三角形 b m 一的面积之比的最大值，他并不是求面积之比，他是面积之比的最大值。你从这个结果来看啊，问题的结果来看，既然是面积之比的最大值，初中学的最大值啊，我们一般来说 就是出现什么呢？要么有范围，要么有范围，一次函数的话，有范围的话，你可以求助最大值啊，你是一个确定的范围，要么呢就是最常见的二次函数啊，顶点是是不是有个最大值，有个最小值， 如果不出意外的话，他应该这两个比出来啊，如果我们将几何比成那个代数的形式的话，比成一个具体的计算题上应该是一个二次的失子，然后我们可以通过配方法求零点四，而且是开口向下的， 也说他也是富人，就是我们摄像的话啊，最后我们可以去做一做，看一下是不是这个摄像，然后求出最大值，是吧？好，嗯，那么想是这样想的，接下来怎么做呢啊？做题我们来具体来说一下 啊。第一，我们知道一点是五五， m 点是负一五，这个可以快速去做， q 点是一个动态的点，是吧？一点，所以导致了一点的运动啊，我们接着看本题的破解方法，我们还是转化思想，将复杂问题呢简单化。面积之笔呢，我们可以转化成线段之笔， 因为这两个三角形呢，他会出现一个什么呢？出现一个高线，这是什么？是一个底不同，高相同的，那么既然他们高相同，所以面积之比就是底之比，所以我们面积经过转化了，面积经过转化之后呈线段之比 这两条线段，这两条线段虽然不是特别好求啊，所以我们有进一步的不好求的线段，我们可以转成好球的线段，那么接下来能用定制的，我们绝对不用辫子这句话是什么意思？等一下会解释啊。最后求出最值的问题啊，几何问题，我们答应说，说白了就是把 啊这种线段之笔变成一个最后一个四字来求最直。好啊，接下来具体的过程，首先我们利用高相同做第一次转化，那么三角形 b 一 q u 这个三角形和上面的 b e m， 他是面积之比，刚说了高线相同，所以等于，哎，等于什么呢？线段之中就是 q e b e m， 而斜线呢，是不好求的，斜线呢，不好求，这里我们在坐标系里面就有一个大原则，因为斜线呢，你要去求的话，往往运用勾股定力，勾股定力就出现二次的事，或者会开二次，是吧？根号比较复杂，那么之后我们就会利用一个什么原则呢？横平竖直原则， 横平竖直，因为我们线段啊，坐标啊，都是横向的，很纵向的，只要你利用这个横平竖直线原则的话，那么我们斜的的东西啊，就会更好的处理一点，是吧？这时候我们可以构造一些纵向的线段，或者是一些横向的线段，我们想到线段之比比 笔的问题，是不是可以转化成另外两组线段之笔啊，说白了，这就是一个简单的相似，是吧？好，这时候横向线段会更好求一点。来，我把辅助线展示一下横向线段，比如说我做了一个横向的线段，横向线段做出来了之后，我们可以轻而易举得到了 bm 平行 qn， 所以 m q e b m e 就等于什么呢？ q n b m 啊，这里啊， q n b b m， 而这个 b m 是特别好求的， b m 是特别好求的，为什么说这个 b m 好求呢？因为两个点坐标都知道了，好， b m 等于几呢？六、 唯一难复杂一点的就是这个 qn， 而 qn， 其实到横向线呢，就很简单了，我们只要把坐标找出来，然后坐标相减，横向线呢，很多标 相减必然可以求出来。好，我们写出 q 点坐标， q 点的很多标是 m， 重坐标是 m， 方寝是 m， 那从而得到 n 点的坐标，因为 n 点的 n 点的重坐标和 q 点重坐标一样，他又在 y 点 x 上，所以他横中坐标都一样。最后我们就求助 qn， 得到一个四字，从而得到 qn 比比六，得到了一个 a， 这次虽然是一个二次的四字，二次次是我们典型的二次函数思想， 是吧？好，配出顶点式，这个顶点式一配出来，我们毫无疑问开口向下，所以最大值就是 m， 取二分之五，而告诉我们 m 范围呢？领导，五之间，嗯，是可以取的， 得到的是最大值二次十分的二数，所以这题就做出来了。好，这题考察的是相当于是二次函数跟我们的三角形的面积， 然后涉及到了呃，面积的转化，变成线段比，最后将线段比，通过一些相似的指数或者说平线分线段成比例的，是吧？就是 啊，得到另外好球的线段之比。最后利用利用啊，函数思想，函数思想求出他的机制 啊，今天的题目就讲到这里啊。

黄冈九年级新课，大多学校都学到相似的，那很多家长就问杨老师有没有往年的中考答题卷，给孩子练练手。我最近也是花了很多时间，把湖北省二一到二五年的中考答题全部整理了一遍， 专门针对黄冈市的考生整理了一套中考真题，会编和解析，有需要的都可以回复真题领取。 其中二一到二三年黄冈市是单独命题的，可以看看以前黄冈的考试模式和难度。 二四年和二五年统考放在后面，这个是必须要去做的，就是这两年统考的试卷模式、考点和题型，值得做完再研究一下。中间二二年和二三年的襄阳、宜昌、恩施实验这几套很有代表性的试卷我也放在里面了。 为什么要放这些试卷呢？大家可以看看这两年统考命题老师是从哪里出来的，我觉得还是有必要去练习一下的。最后两套试卷是二四和二五年的武汉卷，这两套试卷难度是大一些的，有些难题没做出来也没有关系， 可以先熟悉下武汉卷的考题类型，说不定哪年就全生统一了，到时候武汉的试卷还是有一定的倾向性的，提早练习，有备无患。