tan(α-β)诱导公式推导
粉丝6440获赞2.4万
相关视频
 02:02查看AI文稿AI文稿
02:02查看AI文稿AI文稿大家好,我是罗老师,贪奸 t 括号 a 减 b 的公式是什么?贪 j t 括号 a 减 b 的公式如下,贪 j t 括号 a 减 b 等于贪 j 的 a 减去贪 j 的 b 除以一,加上贪 j 的 a 乘贪 j 的 b。 好,我们来讲解下这道题。咱们都知道有一个上述关系是摊间的 r 发等于三, e r 发除以口三 e r 发,所以摊间 t 括号 a 减 b 就等于了三 y 括号 a 减 b 除以口三引括号 a 减 b, 而又因为三引括号 a 减 b, 它等于三引 a 乘 乘以口三以 b 减去口三以 a 乘以三以 b, 而口三以括号 a 减 b, 它又等于口三以 a, 口三以 b 加上三以 a, 三以 b。 所以我们把这两个公式啊,带入这个式子,咱们就得到摊间题,括号 a 减 b 等于 c 影 a 乘口三影 b 减去口三引 a 乘三引 b, 然后再除以口三引 a 乘口三引 b, 加上三引 a, 再乘以 散引 b。 那我们要出现的是摊间 ta 摊间币,所以我们要利用这个商数关系来化解,也就是分子分母同处。以 口三以 a, 口三以 b, 咱们就得到一加上摊间题 a 乘以摊间题 b, 再分之摊间题 a 减去摊间题 b。 那这个呢?就是潘建立括号 a 减 b 公式的一个推倒过程,有看懂吗?我是老师,关注我,咱们下期再见!
22罗姐数学 01:28查看AI文稿AI文稿
01:28查看AI文稿AI文稿大家好,我是罗老师。摊间梯括号 a 加 b 的公式等于多少?摊间梯括号 a 加 b 的公式如下, 摊间题,括号 a 加 b 等于一减摊间题 a 乘摊间的 b, 再分之摊间题 a 加上摊间的 b。 好,我们来讲解下这道题。 摊间梯括号 a 加上 b, 它等于餐饮,括号 a 加 b, 除以口塞饮,括号 a 加 b。 然后根据正弦和与弦合的公式,我们拆开就有三引 a 乘以口三引 b 加上口塞引 a 乘以三引 b, 再除以口塞引 a, 口三引 b, 减去三引 a 乘以三引 b。 好,我们分子分母同时除一个口三引 a, 口三引 b, 那么就得到了一减去摊间 ta 摊间 tb 啊,再分针 贪奸 ta 加上啊,贪奸 tb。 所以贪奸的括号 a 加 b, 他就等于 一减摊间的 a 乘摊间的 b, 再分支摊间的 a 加摊间的 b。 这就是这个公式的一个推倒过程。有看懂吗?我是罗老师,关注我,咱们下期再见!
83罗姐数学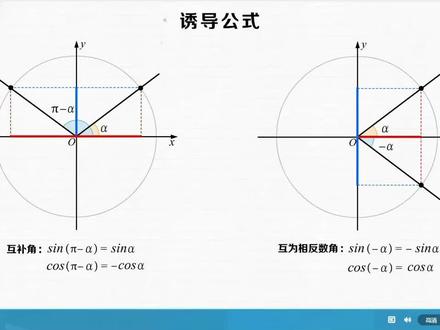 05:02查看AI文稿AI文稿
05:02查看AI文稿AI文稿所谓诱导公式,就是利用角的周期性,把角度比较大的三角函数转换为角度比较小的三角函数的公式。诱导公式有六组, 第一组公式是关于尔法和 k 乘以二拍加尔法的,由于他们的中边相同,所以对应的三角函数值相等。再以 k 乘以二拍加尔法等于相应尔法。 cosine k 乘以二拍加尔法等于 cosine 尔法。 cantone 的 k 乘以二派加尔法等于 cantone 的尔法。可见二派是三种函数的周期。 第二组公式是关于尔法和派家尔法的,由于他们的中间关于圆点对称,所以和单位圆的焦点也就关于圆点对称,即余弦值瞬间值 互为相反数。萨引派加尔法等于负的萨引尔法。抠萨引派加尔法等于负的抠萨引尔法。至于正切负号抵消,所以正切值相等。 tangent 派加尔法等于 tangent 尔法。 第三组公式是关于阿尔法和副阿尔法的,由于他们的中标关于 x 轴对称,所以和单位员的焦点横坐标相同,即直线值相同。 cosine 副尔法等于 cosine 尔法。 纵左标互为相反数,即正弦值互为相反数。散与负而法等于负的散引而法显然正切值与互为相反数。 tanjin 的负而法等于负的 tanjin 的而法。 第四个公式是关于尔法和派减尔法的,由于他们的中边 与歪轴对称,所以和单位圆的焦点纵坐标相同,即正弦值相同。萨引太减,而法等于萨引,而法长坐标互为相反数,即余显值互为相反数。抠萨引太减,而法等于负的抠萨引,而法 显然正切值也互为相反数。 tangent 派减尔法等于负的 tangentr 法。 我们再来回顾一遍这四组公式。第一组说的是二派,是三种函数共同的周期,函数值都不变。 第二组说的是派是正弦和余弦的半周期函数值,符号会改变,但派是正确的周期,所以函数值不变。第三组说的是互为相反数的一对角,他们关于 x 轴对称, 所以余弦值相同,正弦值相反,正切值也就相反。第四组说的是一对互补角,他们关于外轴对称,所以正弦值相同,余弦值相反,正切值也就相反。 那么怎么记住这四组公式呢?我们发现所有这些等式都有两边的三角填数名都是一样的, 唯一要注意的就是函数值虚伪票加负号,也就是符号问题。那什么时候加负号,什么时候不加负号呢? 我们可以把尔法默认为第一象限的锐角,根据 k 乘以二派加尔法、派加尔法、负尔法、派减尔法这些角所在的象限来判断相应函数值的符号。 比如,对于派加尔法,由于默认尔法是锐角,那派加尔法就是第三项线角,于是马上知道他的正弦值要加负号,余弦值也要加负号,正切值不变。 再比如,对于负尔法,由于莫言尔法是锐角,那负尔法就是第四项线角,于是马上知道他的余弦值不变,正弦值要加负号,正贴纸也要加负号。 再比如,由于派减阿法,由于默认阿法是锐角,那派减阿尔法就是第二项线角,于是马上知道他的正弦值不变,余弦值要加负号, 正确值也要加符号。所以总结成一句口诀,就是函数明不变,符号看象限。 不过要注意的是,虽然我们在记忆公式的时候默认角阿法为锐角,但实际上这些公式适用于任意角。比如就算阿法是钝角, cosine 拍加尔法依然等于负的 cosine 尔法,此时的复 cosine 尔法反而是证据。 所以我们默认阿法为锐角只是一种使用特例来记忆公式的方法。 利用这四组诱导公式,就能把任意角的三角函数转化为我们最熟悉的未角三角函数。
1223松果说数学 02:41查看AI文稿AI文稿
02:41查看AI文稿AI文稿有同学跟我说,老师,三角函数的诱导公式,这也太多了,我记不住呀。然后我就说呀,三角函数的老公式不用每一个都记呀,他有口诀呀。同学说,我知道呀,他叫即便偶不便符号看相线嘛, 但是我不会用呀,我不知道什么意思呀。不要怕,孙老师,今天呢,就用两个小工具来帮助大家迅速的理解这句话。首先呀,我们要先做好我们的准备,第一个工具是我们的都是天才坐标系, 第二个工具就是你的手。那我们现在先来看第一个撒印,二分之派加二法。首先要看鸡变藕不变,那什么是鸡,什么是藕呢?他们是二 分支派的系数。那变和不变指的是什么呢?指的是我们函数的名字。 那我们看啊,对于三眼二分之派加阿发来说,二分之派是二分之派的一倍,那一是基数,所以我们函数的名字需要发生改变,变成抠散。阿发, 那符号看信号线,请说,把你的手伸出来。哎,阿尔分支派是不是在我们中间的这个位置, 他加上了一个阿法,加上了一个比九十度小的角,是不是去了第二象限?三也在第二象限,通过我们都是天才看出他是正的,哎,好,符号就为正。再来看一个,比如说 三引,二派加 f, 我们说二派,他是二分之派的四倍,对不对?那四他是一个偶数,我们说函数的名字不变,就写上三引 r 范。 那这个时候我们来看二派呢,他在这个位置,你加上一个比九十度小的脚,他去了第一象限,第一象限三引为证,所以他是正的。 学会了吗?那你用这种方法呀,快速的算一下我们的三音复阿法是不是就是我们的负的三音阿法? 我们的三印派加阿发派加上一个阿发是不是就是我们的第三项线负三印阿发?哎,如果学会了的话呢,你就会知道他 不仅仅对于我们三也好用,他对我们口算同样好用。如果学会了,那就快去试一试吧。
6951讲数学的暴躁孙













