频率概率题型及解题方法
hi, 同学,今天呢,跟着老师一起来学习第三章概率的,进一步认识第二小节的内容,用频率去估计概率。 我们第三章呀,总共就是两小节的内容啊,用频率去估计概率。这一部分的内容其实在我们北师版七年级下册当中就学习过,我们就是用频率来估计概率的, 在这里呢,我们把它拿出来之后呢,再重复的去理解一下,深化一下,深化一下。好, 本节课的重点知识内容大纲呢有两条,第一,通过大量的重复实验可以用频率来估计概率。我们在七年级下册学习的时候呢,就是用这样。首先呢,一般的是吧,必须通过大量的重复实验 啊,重复实验啊,重复实验可以用频率来估计概率啊,那么频率和概率之间是一回事吗?为什么用频率来估计概率?怎么估计?对不对?这个呢,都是需要大家去思考的问题。 带着这些疑问呢,我们一会一起去复习加。呃,这个新授啊,加这样的一个内容,我们再来理解一下用频率去估计概率的这样一个内容。第二点呢,就是说 理解模拟试验的操作与意义,这个呢在我们课本的七十页呀。呃,我拿的这个课本呢是七十页哈。呃,同学们注意可以自己去看一下啊,他有个读一读写的模拟试验,就是说在一定的条件下,你比如说现实当中,呃, 很复杂是吧?我要是去现实当中去做这个事件,做这个试验太复杂,呃,费时费力或者限制很多条件限制不能去做,那么我们就相对应的找一个模拟试验, 模拟试验呢,他就是利用替代物模拟实际事物而进行的试验。 这个内容呀,在我们的啊习题三点四里面会有使用到啊,所以说到时候呢会再进一步的去理解啊,去理解。同学们,在这里呢,要求同学们去看一下模拟实验的,读一读也很容易理解, 就是说我做一个实验他比较复杂啊,东西很多或者是很不方便,那么我你比如说了我,呃弄一些 小球啊,把它编成号码,然后呢从中呢去做这个重复实验去,呃求到某一些事件的概率,就是这个意思哈,就是替代一下,利用替代物啊,利用替代物去模拟实际事物而进行的实验。 好在这里呢,嗯,我们七年级下册的时候呢,就是通过抛制硬币啊,抛制硬币 得到的这个是这个用频率来估计概率啊,频率和概率之间的一些问题,我们在这里呢还是采用同样的,我们没有采用课本上的生日的那个问题,还是采用这个啊,我觉得更容易理解啊,更容易唤醒 大家的记忆。这因为硬币四百次,每隔五十次记录呃正面朝上的次数,并计算正面 毫升的这个频率,你看下面的都是这样,五十、一百、一百五两百,一直做四百次试验啊,五十次的时候呢我就,呃计算一下啊,计算一下,通过这个计算呀, 通过这些大量的实验啊,我们可以转到下面的这个,这个这个叫什么?呃,这个折线图上啊,这是这这种这种坐标图上,那我们来看一下,看一下之后呢,我们会发现啊,他的这个正面朝上的这个频率,他就是稳定在零点五附近。 李维,呃,然后呢,我们用这样的一个呃频率去估计了他的概率,是吧?这里是四百次,是不是在我们七年级下册的时候,如果同学们还能想起来,我们还有国内外的很多科学家,他做了大量的实验,是不是不仅仅是四百次,四万次都不止, 得出来的结果呢?和这是一样的啊,就是硬币正面朝上,或者是呃,这个反面朝上,他的概率,他的频率呢?都稳定在零点五附近。所以说呢,我们用零点五作为了他的概率,作为了他的概率。好, 这个内容呢,都是咱们先前的,我就是帮助大家回忆一下,回忆一下哈。抛出一枚均匀的硬币,硬币落地后会出现哪些可能的结果?问题一啊,问题一,会出现哪些可能的结果?只有两种结果吗? 对不对啊?只有两种结果,正面朝上或反面朝上啊。有的同学说他落下来正好卡住啊,正好卡住啊,立起来了啊,这种结果不算啊,这种结果不算,我们只计算正面朝上和啊,这个反面朝上的这种情况啊。第二个呢,就是说他们的概 是多少?刚才我们已经说过了,我们用频率估计它的概率呢,得到二分之一。那么在实际制硬币的过程当中会出现什么情况呢?会出现什么情况?同学们,我有没有情况出现?前五十次我抛制的时候都是正面朝上, 在我试验比较少的时候,你比如说我就不想做五十次,我累了啊,我就做五次,你有没有可能你的五次做的全部都是正面朝上,那你此时你能说正面朝上是一定的吗?他的概率唯一百分之百不会出现反面朝上的情况, 不可以,对不对?所以说在这里能够得到一个结论的是什么呢?就是说我们要是用频数啊,频率去估计概率,那么这个试验的词数次数啊,一定要大,一定要大,这样的 的话呢,他才比较呃准确,比较准确,这就是用频率去估计概率的时候需要注意的地方啊。并不说你做一次啊,那做成一次那能行吗? 做成一次反面朝上把概率为一,正面朝上概率为一,那你这个东西就没法没,没法研究了,对不对?所以说在这里呢一定要注意这个区别啊,注意这个区别,注意思考。 好,我们简单小结一下,因为用这个内容呢是我们学过的,通过大量的重复实验啊,可以用随机事件发生的频率。什么叫随机事件? 就是说我你这个事件,呃出来之后呢,我无法预知他的结果,对不对?他就叫随机事件啊,发生的频率 啊,事件发生的频繁程度来估计该事件发生的概率啊,也就说频率呢是事件发生的频繁程度,而概率呢是事件发生的可能性的大角 啊,你说越频繁他的可能性越大啊,是有一定的关系,但是呢并不能相等,并不相等啊,这个区别我想大家在七年级学习的时候呢,你们各自的老师啊,都给自己做过区别。 再一个一般的在大量重复试验下,随机事件 a 发生的频率 n 分之 m, n 是试验的总次数, m 是在 n 次试验当中,事件 a 发生的一个次数会稳定到某个成数,这个成数呢,我们在这里呢,用 p 来表示啊,会稳定在这个乘数附近,某个乘数附近,于是我们就用稳定的这个乘数啊,来估计, 来估计事件 a 发生的概率。 g p a 等于 p, 这个能理解吧?啊?这个很简单哈,这个是我们先前学过的啊,先前学过的,我们在这只为做一个复习, 然后呢,我们再来复习一下呢,就是说来这个频率和概率它本身的一个区别哈。在实际问题当中,若事件的概率未知,那么常用频率作为它的估计值啊,频率作为它的估计值, 那么在十,呃,这个区别呢?就是频率它本身是随机的啊,在试验前不能确定,所以说它是随机事件,随机事件做同样次数或不同次数的重复试验,得到的频率都可能不同, 这句话要注意理解哈,就是我刚才说的,你比如说我织硬币,我织了前五次,他是不是有可能都是正面,但 同时也有可能都是反面,但同时也有可能有正面,有反面, 对不对?这就是频率的问题啊,这就是频率的问题,他每次试验了都不能确定结果啊。 但是概率是一个什么?概率是一个确定数,是一个确定数,他是客观存在的,与每次试验无关。也就是说频率是变化的,而概率不变,你不知道他的概率是二分之一,那就是二分之一,而频率呢,就不一定了啊,也许,呃,这呃都发生啊,也许连续发生,也许不发生, 对不对?只有在大量的重复实验的过程当中,频率才能去估计概率啊,概率是针对大量的重复实验而言的,大量重复实验反应的规律并非在每一次实验 都发生,这也能理解对不对?他只是或呃颠倒着说了一下啊,颠倒着说了一下,那大量重复的实验我无法完成,有很多在实际生活当中并不能 实现,那么呢,就用样本频率去估计一下总体的概率,所以说是估计总体的概率哈,并不代表你就一定是准确的概率,这就是频率和概率的一个区别啊, 就是说概率它是一个确定的数值,而频率呢是随时变化的啊,是随时变化的。 注意这个内容不能说了,频率就是概率,这种说法就不对,在这里重点注意一下这个。第二个呢,就是注意一下我们在计算的时候呢, in 分之 m 他的这个计算方式,计算方式啊,你估算的时候你总得拿这个呃公式去估算明白。 ok, 下一个哈,练练,我们来看一下哈。我们来看一下这个 生产瓷砖的时候,一块砖批放在炉中烧制,可能成为合格品,也可能成为次品和废品,对不对?对于一块砖批来说,要么烧合格,要么烧的次品, 那么究竟发生哪种结果,在烧前无法预知,所以说这是一种随机现象对不对?你在烧之前你肯定用的同样的土,打的同样的大小是吧?放在一个炉子里面啊,然后呢都推到火里面,火的温度也是一样的进行烧制, 但是出来的就有不合格的对吧?就有不合格的啊,而烧制的结果是合格品呢,它是一个随机事件,这 这个事件的概率呢?称为合格品率,也就是说求合格品率的话,就是求合格产品的概率,对吧?好,由于烧制结果不是等可能的啊,不是等可能的,因为你烧制的结果肯定合格的多嘛,不合格的少, 对吧?啊?不是等可能的。也就是说,你看我们先前我们在呃这个三点一的第一课时,第二课时当中研究的都是等可能实现啊。我们在第二个课时中专门讲了一下,你比如说他在他在取这个颜色的时候, 呃呃,是不是有有一种他就是不是不等,不是等可能的,那么我们还要把它化成等可能的。然后呢去研究啊,用树状组合列表法。树状组合列表法研究的前提呢,就是他必须是等可能的时间啊,而在这里呢,就有不是等可能的时候 啊,我们常用品合格品的频率作为合格品率的估计值,这是给你说了一下,给你说了一下。好,那么我们往下看,某瓷砖厂对瓷砖进行质量抽检,结果如下, 抽上面的是瓷砖的砖数后,下面的是合格品数,那么合格品率呢?就是 n 分之 m 啊,用第二行的 m 除以第一行的 n 得到一个数值。第一位要求计算上表各组合格品的频率, 精确到小数点后位。后三位啊,注意后三位的表述。第二个呢,是估计这种瓷砖的合格品率,也就是计算概率了哈,精确到零点零一,小数点后两位。这个呢,一定要看准啊,看准有很多同学呢就是先入为主啊。 第一个,呃,是这个,呃呃,零点零三和小数点后三位。第二个也是啊,就这样,瞎说啊,瞎写。第三,若该厂本月生产该型号瓷砖是五十万块,是估计合格品书,如果我们制造合格品率 是吧?我们用五十万去乘以那个合格频率,他就是估计出来的合格品数,对吧?啊,这个很好理解啊,很好理解啊,这比前面的竖状图和这个列表法还好理解。嗯, 好,经过计算呢,我们把下面的表填一下就可以了哈。同学们,那么观察上表,你看,零点九五,零点九六九五,九六九六九六九六九六,九六,是不是都是在九六附近啊?都是在九六附近。这个,呃,这个叫什么波动 啊?所以说我们估计该型号瓷砖的合格频率呢,为零点九六。第三位,五十万乘以零点九六,直接等于四十八万块啊,那么我可以估计该型号合格品数为四十八万块啊,就是估计一下啊,估计一下,我不可能五十万块,我不可能一块一块去看吧, 对不对?那也不符合实际生产的需要。好,第二题,一个水塘里面有鲤鱼、鲫鱼、鲢鱼公一千尾,一千尾, 谁多谁少不知道是吧?然后呢,怎么一渔民通过多次捕捞实事验后发现哈,呃,这个鲤鱼鲫鱼出现的频率呢?是百分之三十一和百分之四十二,也就说我捕捞以往我看数一数捕捞以往数一数,我多捕捞我就是没事了我就捕, 我没事了我就普捞啊,因为我也不知道他们现在到底还有几条啊。我,不,我也不可能都抓,都捞出来是吧,我都捞出来数一数,那也不可能,所以说呢,我们在前面总结的时候,是不是有有一种呢,就是用样本频率去估计了一个总体的频率了,对吧? 那么在这里呢,我们就可以看啊,鲤鱼出现的是百分之三十一,那么你总共是有一千尾,那么估计的话,鲤鱼是不是有百分之三十一乘一千三百一十条,对吧?嗯,鲫鱼出现的是四百分之四十二,那么就四百二十条, 看看人家最后千万不敢写三百一十条和四百二十条哈,人家问的是鲤鱼和鲢鱼的 是不是你用一减去百分之三十一,百分之四十二得到的那个二十七,百分之二十七,是吧, 这才是连鱼出现的频率了啊,在这里千万要注意哈,总有很多陷阱呀,是同学们,就是总有很多陷阱,咱觉得应该避免,但是呢,呃,还是有人跳啊,而且跳的 次数很多啊,虽然说这个同一个地方不能绊倒两次啊,但是在我们的这个呃,学习过程当中哈,同一个地方绊倒两次的现象比比皆是啊,比比皆是,所以说同学们一定要注意哈,多用心一些 好,第三题也是池塘养鱼的这个问题哈,这个问题,但是呢,他这个呀,又搁和数据统计呢,稍微有点关系哈,我们来看一看, 某池塘里养了鱼苗十万条啊,十万条更不可能抓出来去干了哈,根据这几年的经验和鱼苗成活率 呀,为百分之九十五,也说我养了鱼苗是十万条,但是鱼苗整着整着成活,成活的时候成活率只有百分之九十五, 百分之九十五啊,注意,并不是所有的东西,并不是所有的鱼苗都能成活一段时间以后准备打捞出售啊。养好了准备打捞出售。第一网捞出四十条称的平均每条鱼重二点五千克。啊,还挺重的是吧?二点五千克是五 啊,五斤对不对啊?第二网捞出了二十五条称,在平均重量二点二。第三网捞出三十五条称平均重量是二点八千克啊,你看养的非常好啊,养的都很重。 呃,那么是估计这池塘中鱼的总质量,请问鱼的总质量应该怎么弄? 我如果知道每一条鱼的这个平均重量 或者乘以它的数量是不是就是总质量了,对不对啊?我就求一下每一条鱼的这个平均量,因为它不可能长得一模一样嘛,对不对?我只能求求出来它的平均重,然后呢去乘以它的这个数量, 得到最后的结果。那么一条鱼的平均重量是多少呢?就根据这个去求啊,有数量有重量,有数量有重量,对不对?求下的平均四十乘以他,二十五乘以他,三十五乘以他,然后再除以总条数是不是就得到每一条鱼的 这个平均重量,然后呢再用平均重量乘以十万乘以成活率的百分之九十五就能够得到总质量,对不对啊? 很简单啊,很简单,甚至在小学的时候我们就会计算就会计算。那在这里呢,我们只是提升了一下啊,提升了一下, 但是本质上呀,本质上算起来还是差不多的啊,还差不多的,注意单位啊,注意单位,注意答好同学们这节课呢相对比较简单。嗯,所以说呢,我们也比较。
粉丝2.9万获赞7.7万
相关视频
 07:29
07:29 11:26查看AI文稿AI文稿
11:26查看AI文稿AI文稿这个视频我们来讲一下频率。概率,那我们以抛硬币为例,我们来讲一下频率与概率之间的关系 啊,我们抛这个硬币是质地均匀的硬币,那他我们知道抛硬币正面朝上和反面朝上两种结果,质地均匀,那么他的概率值呢?就是 二分之一,这是一个理论值。但是我们实际去这个抛硬币这个实验中,你比如说我们第一个,我们做了十次实验, 抛了十次硬币啊,抛了十次硬币,那你你抛出的结果那有可能是三次正面朝上,那七次反面朝上,那么要求的是正面朝上的概率,那就是正面朝上的频率。 这次实验呢,我们算出来的这是频率,那那就是正面朝上是三次,然后总次数是十次,那他的频率呢?就是十分之三,十分之三,这是频率, 那但是它的概率,这概率是二分之一, 概率是不会变的啊,概率是二分之一。抛肢体均匀的硬币,那你正面朝上,反正朝、反面朝上是等可能的,那么概率是二分之一。但是我们做实验,我头抛十次,那么他们是 正面朝上,有可能十三次正面朝上,那也可能。你再抛十次的话,那有可能两次正面朝上都有可能啊,那这个只因为这个实验的次数少, 那么这个我们算出来是叫频率。频率,那我们把它加大次数,你比如说我们一千次,一千次,你做这样的实验的话,你就会发现正面朝上和反面朝上的次数,呃,接近于五百次,那你比如说正面朝上的次数是四百九十四, 那反面朝上的次数是五百一十次,那他的频率呢?就是四百九十除以一千啊,接近于二分之一,接近于二分之一,那你如果再做实验的话,一万次或者十万次啊,你比如十万次, 那十万次,那你做这样实验的话,那就会发现无限接近于,那也无限接近于这个二分之一啊,他就会更加接近 二分之一,那么通过这样的实验,但是随着这个实验次数的增加,也就是我们抛硬币这个重复次数的增加,那么这个他的频率,这是频率,那么频率就会稳定于 这个事件的概率,这个事件呢,就是我们正面朝上这个事件这个时间的概率,那么这就是我们叫频率的稳定性, 频率的稳定性,那么也就是说随着我们实验次数的增加, 那事件 a 发生的频率呢?会逐渐的稳定与事件 a 发生的概率,那也就是通过这个那次数啊,随 实验次数增加 增大,那么频率就会稳定于概率。 根据这个理论我们就可以,如果这个你这个实验的次数,实验的次数多了,那我们算出来这个频率呢?我们可以用算计算出来的频率来估计概率啊,就是用频率 去估计概率, 那这就是频率的稳定性,我们看客户的练习,第一个是判断下面说法是否正确,并说明理由。那么抛至一枚硬币正面朝上的概率呢?是零点五,则抛至两枚硬币 一定是一次正面朝上,一次反面朝上,那么这个是显示错误的,那你抛至两枚硬币正面朝上和反面朝上都是概率是零点五呢?我们抛至 一枚硬币是正面朝上,然后两枚硬币,那有可能啊,正面朝上,反面朝上,两枚硬币,那么一枚硬币正面朝上,一枚硬币反面朝上啊,那两枚硬币, 那也我们就可以分成啊,这个基本样,整个样本空间呢,就会是这个正,一枚硬币是正的,那么第二枚硬币呢?可能正,可能是反, 然后一枚硬币反的,那么这个第二枚硬币可能正,也可能反,总共有这四种整个样本空间,就是有四种可能,那 他说一次正面朝上,一次反面朝上,正面朝上,反面朝上,正面朝朝,正面朝上,反面朝上,那么他占了总共四个整个样本空间,四个样本点,那么这个事件呢?占了是 一半啊,占了两个,占了两个,所以说它的概率呢?我们用古典概型的话,是二分之一,而不是一定不是必然事件啊,它是二分之一,不是必然 时间,所以说是错误的。那么第二个抛制一枚质地均匀的硬币十次,结果四次正面朝上,四次正面朝上,那我们得出来的是频率,这是一这次实验,那么是 正面朝上的次数四,除以这个十,那么就是频率零点四啊,不是概率啊,正面朝上的概率是零点五,这是固定的理论值,这是我们是频率啊,不是概率, 所以说这个也是错的啊,把这个概率改成频率就对了。那么当实验次数很大时,随机事件发生的频率接近于概率,那么这就是我们频率的稳定性。那么当实验次数很大, 那么你这个频率是稳定在这个概率,那么这这个时候我们是可以用频率去估计概率的,所以说这个是正确的。第四是在一次实验中,随机实验可能发生,也可能不发生,所以实践发生和不发生的概率是各是零点五,这么这个也是错误的, 那么他可能发生和可能不发生,那他的概率不一定是一样的啊,不,不一定是等可能的。你别说打靶,打靶要么中靶,要么不中靶,你打靶有些水平高,那么他的中靶的概率 重把的这个概率呢?是比较大的,比如说我有零点八的概率,那么这个时候他是重把和不重把,这个发声和不发声,他们就不是等可能的。那么所以说这这个这个题就是错误的。 这第一题我看第二题用质两枚硬币做胜负,游戏规定两枚硬币同时出现正面和同时出现反面算假胜,一个正面,一个反面算以胜,那么这个游戏公平吧? 公平不公平,那么就要看这两个假胜和已胜,他的概率是不是二分之一,都是二分之一,如果都是二分之一,那就说这个游戏是公平的。那我们来看一下那两枚硬币同时出现正面和反面 叫假胜。那我看整个样本空间,样本空间,那么整个样本空间呢?就是你要么正正这是一个,然后是正反,这是一个,然后反正这是一个,然后是反反, 这是一个。总共四个样本点啊,这是四个样本点,样本空间,那么假剩,我们看一下假剩这个他的样本点,假剩的这个样本点呢?是只要是正面出现,同时出现正面,那就是正正, 还有同时出现反面,那就反反反,那么都算假胜,那么这是两个样本点,两个样本点,那我们它的概率呢?就是二比四二分之一, 那么同样这个已胜呢?已胜他的样本点是正反和反正这两个,那这个概率呢?就是 也是二分之一,所以这个假胜和已胜的概率是相等的,那么所以是公平的啊,这个游戏是公平的。这第二题第三,根据统计 a、 b、 o 血型具有民族和地域地区的差异,在我国这个 h 省调查了三万多人,那么这四种血型人数如下, 那么这个这个这个啊频率我们怎么算呢? a 血型,那总人数是三万零四百八十八,那么他 a 血型呢是七千七百零四,我用七千七百零四除以这个总数,那么就是他的频率, 那么我们经过计算,我们得出来是这个是频率呢是二百 分之二十五点三,而这个 b 呢,我用一万零七百六十五除以个三万零四千四百八十八,那么他除以这个总数,那么就得出来是他是占了百分之三十五点二,三十五点三, 这个呢是占了百分之二十九点四,这个呢占了是百分之十点一零, 那我们精确到啊,精确到零点零一,零点零一,那么就是这个啊,就是零点二五三,这个是零点三五三,这是零点二九四,这是零点一零零啊, 那这是第一问就解决了把把这个频率,就是用这个他自己这个数人数,那除 补一总数就可以。那么第二个呢是如果从一个 h 省任意调查一个人的血型,那么他是 o 型血的概率,那么这个是我这个是三万多人,三万多人这个人数足够多,那我们是可以 用频率,我们这个频率来估计这个概率的,那 o 型血这个频率呢?是百分之二十九点四,那么这个概率, 那么就是 o 型血的概率。我随便抽一个人,他如果是 o 型血,那么他的概率呢?是百分之二十九点四。
85洪邦数学 07:29
07:29 10:17查看AI文稿AI文稿
10:17查看AI文稿AI文稿哈喽,同学们大家好,我是栗子老师,一日不见,甚是想念。今天我们来学习用频率估计概率。好,我们来先来看一下本节课的学习目标,理解用频率估计概率的方法,并应用 好新课讲解用频率估计概率。我们先来看一个织硬币的实验,抛制一枚均匀硬币四百次,每隔五十次来记录正面朝上的次数,并计算出正面朝上的频率来完成下表。好,我们来看一下 这是什么意思呢?我们来看一下他一共要投这个硬币四百次,每隔五十次我记录一次,那证明我第一次记录的时候是不相当于抛的第一个五十次,对吧?好, 接下来,哇,第一个五十次,他是有二十三次正面朝上的,那第二个五十次是不是相当于是投到一百次了?一共投了一百次硬币,我记录一下正面朝上,一共有四十六次,那接下来依次类推,一百五十次,一共有七十八次正面朝上。好,接下来二百次。 一百零二次正面朝上。好,接下来是二百五十次,一共有一百二十三次正面朝上。接下来是三百次, 一共有一百五十次正面朝上。接下来是三百五十次,一共有一百七十五次正面朝上。好,最后我们到了第八个五十次,也就是第四百次,一共有二百次正面朝上。 好,接下来让我们来算出正面朝上的频率。我们知道频率,咱拿平数除以咱们这个总的这个次数,对吧?那第一个 二十三除以五十四,十六除以一百七十八除以一百五,一百零二除以二百。好,依次类推,我们算出来正面朝上的这个频率, 好,嗯,发现咱们随着咱们这个次数的越来,抛的这个次数越来越多,我们这个正面朝上这个频率,咱是不是大概都稳定在咱们零点五的这个数值啊? 是吧?随着我这个次数是不投的次数越来越多,那咱们这个频率是不是也在区于零点五这个数值?那咱们来看一下,历史上也有一些数学家做了一个织硬币的实验,我们来看一下这些实验数据,通过这些数据我们来看能发现什么规律 好?看。第一个这个数学家,他抛了两千多次,有正面朝上的话是一千一千多次频率,正面向上的频率,拿这个频数除以总的这个抛的这个次数 总共是零点五一八,好。接下来四这个这个数学家,他是抛了四千多次,一共是两千多次。正面朝上算出来的频率是零点五零六九,好,下面是一万次有四千九百 七十九次,好,算出来是零点四九七九,好,一万两千次有六千零一十九次,对吧?六千多次算出来是零点五零一六,那两万四千多次,一共有一万两千多次,那算出来的频率也在零点零零五, 好,那通过这些数据你发现了什么规律呢?那跟刚才咱们那个抛的四百四那个实验是不是比较类似啊?随着他那个次数,是吧?次数越来越多,他是不就大概是趋于在零点五那个附近那个值啊? 是不是越来越趋近,趋近于咱们这个数值,好,这就是我们今天要学的啊。就是当我们在大量 重复的实验中,如果事件 a 发生的频率最后稳定在某一个长数 p 小 p 附近,那么这个长数 p 就叫做事件 a 的概率,记住 pa 就等于这个小 p。 好,咱们注意啊,是在大量重复的实验中, 那刚什么意思呢?我们看刚才,刚才我们这个在投资这个硬币的时候,我们正面向上的这个频率,是不是大概最后在区就是相当于集中在零点五的这个附近,那我们来看一下,那相当于这个小批他就是零点五,那么让我们来计算正面朝上的这个频率,那我们就可以用这个 让我们来算正面朝上的这个概率,那我们就可以用咱们这个频率来估计这个概率,就说 pa 就等于这个小 p, 也就是 pa 就等于零点五,就是说投资硬币中正面朝上的这个概率是零点五,也就是咱们说的二分之一。好, 我们来看例题,第一个判断正物连续制一枚质地均匀的硬币十次,结果十次全部是正面,则正面向上的概率是一。 哎,我们来看一个同学说,哎,老师他就是啊,他,他十四,对吧?我们可以就是他的平数吗?平数除以十,那不刚好就是一吗?那概率就是一。那我们想一想啊,你 硬币他是有正反两面的,你前面十次都投的是都出现的正面,那么你能保证第十一次他仍然出现的是正面吗?如果你能保证的话,他才能说一直是向上,向上概率是一,他必然发生,对不对?但是我们第十一枚谁也说不准,他可能是正,可能是反,他的概率是不是相当还是二分之一啊? 是不是因为他这个才十次呀?对不对?而且你正面向上和正面向下他都是有二分之一的这个概率的。对, 对,你不并不能保证一直他是正面向上的。好,所以说第一个是错误的。第二个小明织了硬币一万次正面向上的频率在零点五附近。哎,这个正确,对不对?他抛,抛了,大概抛了一万次,是不是大概有五千次正面向上?我们前面也做了实验了,是吧? 好,他的向上的频率,而且人家也很严谨,在零点五附近。好,第二个就是正确的。第三个设一大批灯泡的次品率为零点零一,那么从中抽取一千只灯泡,一定有十只次品。 好,我们拿次品率去乘以这个灯泡啊,我们算,哎,刚好有十只,所以说正确,对吧?好,但是这道题啊,他是错误的,他为啥是错误的呢?老师跟大家这里要说一下啊,就是虽然我们拿这个次品率去乘以这个总共的确实算出来是十只,但是我们那个 这个次频率,对吧?咱们拿频率去估计一大批吗?人家说是一大批,我们是拿频率来估计概率估出来的,他这个次频率是零点零一,但是我们知道我们那个实验是大量重复的, 并不一定他是有规律,有随机性和规律性的,并不一定在每一次这个实验中他都成立,所以说可能其他的 可能抽到下一批一千只灯泡里面可能会有十只次品,但是你不能说我从中只要抽取一千只,他一定就有十只次品,这个是不能保证的啊,因为我们是有随机性和规律性的,这个规律他并不一定在每一次的实验中他都发生,因为是大量重复的,有非常非常多。好,这个是错误的,同学们需要注意一下。 好,我们来看 dear 某篮球队教练记录,该名该队一名主力前锋在练习罚篮的时候, 结果如下,这是他那个教练在罚他,就是教练在让他做那个罚篮练习,看我罚你三十次,你能投中多少次?就这个意思。好,第一个他罚了三十次,对吧?罚他三十次来,投中了二十七次来罚六十次,投中四十五次啊,依次类推。好,上面是他投的,罚他投的,下面是他投中的。 好,我们来看一下。第一个让我们来填表,让我们算罚中的频率。罚中的频率是不是让他中了这个次数去除以他罚的这个总次数,那第一个是呢?二十七除以三十,对吧?四十五除以六十。好,我们依次可以把它算出来。 好,算出来这个频率,我们之前也学习过啊,怎么计算频率?第二个比赛中,该前锋队员上篮得分,并造成对手犯规。好,这是他现在来比赛了,对吧?但是他上篮虽然他得分了,但是他造成这个对手 犯规了,所以说这个比赛的这个裁判员啊,就罚让他罚篮一次,罚篮一次,你觉得他这一次就罚了,这次难,他能罚中的这个概率是多少? 好,那我们来看一下啊,他是前面是练习,对吧?练习了很多很多次,他这个次数是不是一直在增加?我们看他随着这个罚篮的这个次数增加他的这个罚重的频率,我们看是不是也在慢慢的 集中在一个数值上,我们发现越来越多,越来越多,一直到五百次的时候,是不是他这前面的大概都集中在零点八附近? 还有他说老师,那这还有零点九呢?零点九他是不是才透三十次啊?对不对?他都是三十次,那是就不属于是大大量重复的实验,对不对?只有他次数够多我们才看啊,这个相当是偶然数据了,所以说我们来看他在大量重复的实验之后,他大概法中的这个概率就在零点八附近。所以说我们看 答案应该怎么写。从表中数就可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在零点八左右,所以估计他这次能罚中的概率为零点八。好,这是我们的解答题,大家需要这样去交代一下,你这道题目就做出来了,就是拿频率,对吧?去稳定他这个,所以说 咱们就是拿频率去估计他这个概率。好,我们来看第三填空。某公司进行内部抽奖活动,一共准备了一百张奖券,共设了 特等奖一个,一等奖十个,二等奖二十个,三等奖三十个,已知每张奖券获奖的可能性相同,就是那个等可能性。那么抽取一张奖券中特等奖的这个概率,我们看一共有只有一张特等奖,对不对?他一共有一百张奖券,那他抽特等奖的概率是一百分之一。 好,抽取一张奖券中奖的概率,那我们来看,不管你特等、一等、二等、三等,只要是你这个奖中了就行,对吧?那咱们中了就行。那咱们的数值大概一共有加和好,一加十、加二十,加三十,比上总的这个奖总,总的这个 券,奖券的张数,那一共就是一百分之六十。一。好,第三个抽取一张奖券,中一等奖或者或者是二等奖,就说你这两个只要中了一个就成,对吧?那一等奖有十个,二等奖有二十个,我把它俩进行加合,十加二十,再除以一百就是一百分之 三十。好,这个等号啊了。好,然后我们来看一下,那么将它进行化减,就是十分之三。好,那中一等抽一张奖券,中一 一等奖和二等奖的概率就是十分之三。好,今天我们主要就是学了用这个频率来估计这个概率,咱们注意啊,就大量重复的实验中,对吧?我们可以就是拿频率来估计概率。好,那咱们本节课啊,就上到这里,同学们记得来评论区完成老师的作业,我们下节课见。
211栗子老师数学版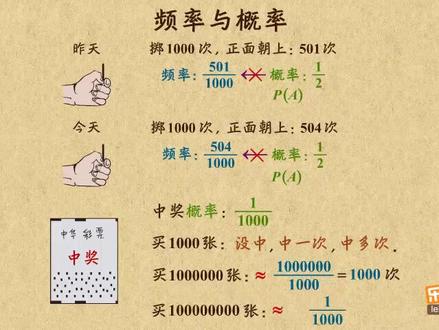 02:34查看AI文稿AI文稿
02:34查看AI文稿AI文稿咱知道,制硬币一落地后,可能正面朝上,也可能反面朝上,但出现正面的可能性有多大呢?这就是接下来要讨论的频率与概率问题。 除了看这俩词,感觉是一回事,但他俩是不同的,那到底有啥区别呢?举个例子吧,昨天我治了一千次硬币,正面朝上的有五百零一次,那频率就是千分之五百零一,概率十二分之一。 今天我继续治了一千次硬币,正面朝上的有五百零四次,那频率就是千分之五百零四,但概率仍是二分之一。 概括一下,频率就是在一次试验中,某一事件出现的次数与试验总数的比值,而概率是某一事件所固有的性质,即做 p a 比较,他俩发现频率是变化的, 每次试验可能不同,而概率是稳定不变的。在一定条件下,你可以用频率进四代替概率,但不等同于概率。 反过来,概率是用统计来定义的,所以也不能直接反映频率的情况。比如,某彩票的中奖概率为千分之一, 那买一千张彩票,结果可能一次都没中奖,也可能中一次,甚至还可能中多次。所以,彩票的中奖概率为千分之一,并不意味着买一千张就一定能中奖。但当所买彩票的数量非常大,假设是一百万是, 那我们可以近似的看成,中奖的次数约等于千分之一百万,也就是一千次,但不能说一定是一千次,只是比较接近他而已。如果数更大一点,比如是一个亿,那中奖的可能性就更接近千分之一,于是中奖 的次数也就越接近千分之一亿,约等于十万次。看来,当试验次数很大时,你可以用概率进四代替频率,但不等同于频率。 了解了频率和概率的区别后,咱再看看概率值的范围。因为在多次实验中,比如是一千字,那事件 a 发生的评书 m 就在零到一千之间,所以 a 发生的概率就在零到一之间。 如果 a 是必然时间,哪一个概率就是一。如果 a 是不可能事件,哪一个概率就是零。以上就是这个视频的全部内容,主要有两点,首先,你得弄清楚频率和概率的区别。频率是出现次数与总次数的笔直,概率是事件固有的性质。 另外,概率的范围是零到一,必然实现的概率就是一,不可能实现的概率就是零。好了,为师就讲到这,快快刷题去吧!
563生哥 02:29查看AI文稿AI文稿
02:29查看AI文稿AI文稿估计概率龙宇地下城龙宇地下城一个只有地图与指示物的桌上扮演游戏,他力求创建一个完美而繁复的世界观。 在这个世界里,只要投资制出适合的点数,玩家扮演的冒险者就能做到一切。生活大爆炸中,希尔顿几人经常度过这样一个跑团之夜, 利用前面学习的列举法,可以计算至投资时某个事件发生的概率。但这种计算有一个前提,即每个点数出现的概率都是相等的。 质地要求投资必须是质地均匀的。但有些赌徒们却不愿意这样纯粹靠运气,为了作弊,会故意制作一些质地不均匀的投资来获利。这时怎么来得到投资各个点数出现的概率呢?长期实践中,人们观察到,对一般的随机 事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率总在一个固定数的附近摆动,显示一定的稳定性。因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计他的概率。 抛硬币会产生最简单的随机结果,正面朝上或者反面朝上。历史上很多人都利用过频率的方法来估计正面朝上的概率。 通过这些毅力惊人的先辈得出的数据可以看到,随着试验次数的增多,正面朝上的频率越来越接近于二分之一,于是正面朝上的概率就可以被估计为二分之一。 用频率估计概率有很多实际应用。一七七七年,法国科学家不锋做了一个实验,他拿出一张画了多条等距离的平行线的纸,又拿出一大把小针,小针的长度 平行线间距离的一半,然后把小针往尺上扔,并记下针落定后与平行线相交的次数,共投置了两千两百一十二次,相交七百零四次,两者比值为三点一四二。是不是和派很接近呢? 以后的很多人都重复了这个实验,并且发现投掷次数越多,比之结果竟然真的越来越接近圆周率,这样实验中真与平行线相交的概率就被估计为太分之一。 福尔摩斯在跳舞的小人案中,需要破解一个画着各种跳舞小人的纸条。福尔摩斯猜到每个小人对应一个英文字母,根据纸条上不同小人出现的频率和英文中不同字母出现的概率相对应,最终确定了每个小人所对应的字母,破解了这些密码。
12己所不欲
猜你喜欢
- 2077老姚











