合工大共创超越模拟卷在哪买
粉丝1.1万获赞13.1万
相关视频
 09:06
09:06 07:18查看AI文稿AI文稿
07:18查看AI文稿AI文稿我们看这道题是和二零二三年数一的第十八题是很类似的,求一个及值问题,那么二月函数无条件及值,这不就是 a c 减 b 方的判距吗?所以我就是先求对 x 偏导, 就等于三 x 方减去二 x y, 这个 y 方求编导就没有了啊。 然后 f 对 y 求偏导,就等于第一个就是负 x 方,加上这个六分之五,这个地方求偏导之后变成二 y 是吧?那就变成三分之五倍的 y, 再加上哎, y 的立方求偏导,就等于三外方,那三约掉了,就是 y 的平方。 那我们令 f 偏 x, x, y 等于零, f 偏 y, x, y 等于零。解一下注点,那这个解的话,你的 解算纸上偷偷快速算一下就行了。你看解这第一个式子的话,它就是 x 倍的三, x 减二, y 等于零。所以 x 等于零,或者是 x 等于三分之二 y。 然后把这个式子带入第二个式子啊,带入这里,那么当 x 等于零的时候,很明显就是这个式子的零了是吧?就是三分之五外加外方也得零了。 那么一种情况就是 y 等于零。还有一种情况就是他这个提供一式之后, y 是不是可以等于负三分之五, 然后 x 等于三分之二 y 的时候也代入第二个式子,呃, x 等于三分之二 y 的时候代入,那于是这就是负的九分之四外方,在 再加外方再加上三分之五外等于零,那这个就变成九分之五倍的外方加三分之五倍的外等于零。把这个五给他约掉。等号两边乘个九,那就是外方加三外等于零。 那这时候如果 y 的零呢?如果 y 的零, x 的零是吧? y 的零带回去 x, 三分之外, x 零零零给咱们。前面不是解过了吗?还有一种就是啊, y 的负三对不对?那么因此还有一组解,就是 y 的负三, y 的负三带进去 x 就等于负二。因此把这个注点写上去,有零零,还有零, 负三分之五,还有负二负三这么几个点。那么注点解完了之后,这道题的第一个难点就来了,就是他有 a, c 减 b 方等于零的情况。这种情况呢,在我们的强化课上都是讲过的,分析过的。 二零一八年不是不是二。这个二零二三年第十八题也考了这样的一个考法了。那想要验证他是不是真正的极值。我们是不是求的 ac 减 b 方啊?那也求二阶偏道, f 对 x, 求二阶偏道,那就是六 x 减二 y, 然后 f 偏偏 x, y, 把这个式子对外求编导,就等于负二 x。 还有一个 f 偏偏 yy, 就等于。呃,把这个式子对外求编导,就是哎,三分之五 再加二 y, 然后我们就看在零零点。哎。这个很明显, a 等于零, b 等于零,这个 c 是等于三分之五的。那么这时候已经是 ac 减 b 方等于零了。我们说这种情况,按照 判别法的话,他是无法确定是不是极值,但其实想到是教材上写了这种情况百分之九十都不是极值。 为什么考场上 ac 减 b 方等于零都不是机制的。你看二零二三年,他那也不是机制,你平时做过习题,他也都不是机制。为什么呢?因为一旦 ac 减 b 方等于零是机制,他要么特别简单,特别弱智,要么就特别特别难。 因为你想证明是极值的话,哎,他要么就是哎,这特简单的。比如 c 等于 x 四十米加外的四十米,哎,这一看就零,零点是极值。你算算这个数字,也是 ac 几元等于零的,或者长成别的样子。总之是特别简单的结果他是极值。要么就是哎,特别麻烦的结果是极值。 因为你得证明所有路径他都是极小的,所所有路径他都是极大的。所以这种情况呢,就不太适合出题目。你将来搞科研可以是吧。啊,这个一时半 想要考场上判断出来特别难的情况,哎,判断不出来呀。所以他就只能出那种不是极值的情况。那么不是极值,就是找特殊路径就行了。那像这种题,找特殊路径,优先思考的就是 x 轴, y 轴。还有 y 等于 x, y 等于负 x 是吧,就这四条。 呃,这几条线就是这个横着的,竖着的啊,斜着的这几条线。然后你就可以讨论,很明显, f 零零是等于零的呀。沿着某些路径,如果有比零大的,也有比零小的,他就不是极值了。 比如说,你把 x 零往里边带, x 零往里边带,它剩下这个平方加立方,立方是高阶五角,它剩下平方,哎呦,这个沿着平方趋近它,真的是机制是吧?这个还不行,那把 y 等于零往里边带的时候呢?哎呦,把 y 往等于零往里边带是可以的呀。所以当 y 等于零的时候,小 f x 零,它就剩下 一个 x 立方了。这岂不是在 x 区零的时候,他有比零大的,有比零小的,看你是零正还是零负吗?所以这个地方他不是极值,有一条路径不是极值,他就都不是极值了。你可以再试试, y 等于 x, 一旦 y 等于 x, 这俩抵消了。 然后这俩一合并呢?还是剩下一个平方?立方是高级武警小,那平方还是机制。所以 y 等于 x 不行。你可以再试试 y 等于负 x, y 等于负 x 也不行。因为这个还是留下一个平方。 所以你就放心大胆的试就行了。试完之后,早晚能找到一些特殊路径。那么因此,哎,证明完了,他不是机制。如果考场上找不到怎么办呢?你就先哎,直接写结论,哎,显然不是机制。对不对,路径不找了。 这样的话,你结果也说对了。步骤分,酌情扣呗。基本上考场上百分之九十这种情况都不是机制啊。这是一个规律。然后别的点呢?再来判断 零。负三分之五这个点,那么 a 给他带进去,这就是六乘以零减去二乘以负三分之五,那么 a 就等于三分之十。哎, b 就等于零吧。哎, c 就等于要把这个 y 带进去,这个是三分之五减去二倍的三分之五, 那么所以 c 就等于负三分之五。这个 ac 一号一看就不对是吧。就是 ac 减 b 方是不是小于零啊。所以这个点啊,不是极值。 那最后一个点该试了吧。啊,负二负三处,那么把这个带入。 a 一算等于负六, b 往里一算的四, c 往里面一算,等于负三分之十三。 那么这时候 a c 同号了,并且一相乘。很明显, a c 减 b 方大于零,并且 a 小于零就是极大。为什么 a 小于零就是极大呀? 因为这就是凹凸性嘛, a 小于零,他就是凸的,那因此在这地方取得几大值,再把它算一下啊。 f 负二负三代入原来那个函数算一下算比较简单,算完之后等于二分之五。 那所以你看这种二元函数及值的题呢?你只要知道这个求解流程啊,背这个公式,很容易就把它得满分了。 而像这种蓝色的不是极值的情况呢,就是这个 a、 c 等于零的情况呢。找一些这个特殊的小技巧,练几个例题也就懂了。然后关于这类题,大家如果有不懂的,可以看看我这个二零二三年第十八题的这个讲解,自己也可以多找一些例子再来练一练。那我们下个视频再见。
24小元老师考研数学 01:29查看AI文稿AI文稿
01:29查看AI文稿AI文稿今天大家试一下两箱的食欲,不是,这太搞错了, 这种车一定第一时间上车,先把阿莫斯打开,电子防滑先关掉,这样才是一台真正的马力, 他小小声的放弃吧,啾啾车马力并不大,秒天秒地秒空气,其实没什么,可能很多欧洲车都已经能超越这台车, 他的强项是放在赛道上面,是很容易去开,就很容易能试到这车的极限。没有任何的智能辅助系统,所有动作都要靠你自己独立完成,开的快不快纯粹就是看你的驾驶技术。 在车友 vita 加 turbo, 但是你完全是没有任何 turbo 介入的痕迹,完全像台大马力的自然吸气,六千数的波沙,非常之神秘。吹油时间呢,很 很长很长,就他的马力输出线性到你是完全不觉得他有什么多大马力,任何时候你都觉得这车很快,而这排挡头的设计我觉得很好用,可以符合你一切的换挡习惯。你坐在车里面,看到头盖有那么一丢丢的凸起来,你就知道这个车不一样了。 不是说车能有多快,但是它就是让你很开心。这台车为什么那么多人去追捧,我觉得性能不是重点,它能让你感受到你回到十八岁, 我开着这台车,我回想到刚刚完车的时候,这台车很容易上手。当跟你的初恋女朋友谈恋爱的时候,就大家不需要说什么,你看着我,我看着你,就有感觉。
1.1万吴子峰玩车 01:04查看AI文稿AI文稿
01:04查看AI文稿AI文稿同学们好!我是数学老师陈振新。我谨代表兰考一高二零二五届高三数学组全体教师, 即将毕业的你们!线线角线面角面面角,崭露头角平行线抛物线双曲线,超越极限。 字变量音变量多变量,前途无量平面图时光图时光图,大展宏图。 既定理,用定理,定定凡心明哲理,列方程,解方程,方方在路好前程。愿同学们以自信为圆心, 拼搏为半径,在璀璨的六月跨出圆满的人生!同学们,奋战百日,共创辉煌!奋战百日,共创辉煌!
2.1万兰州新闻网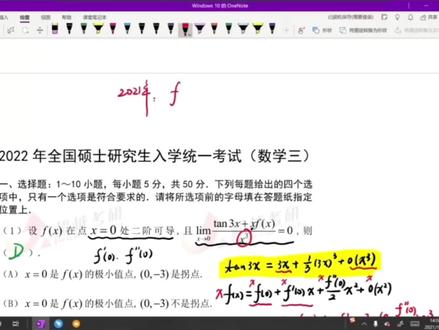 04:33查看AI文稿AI文稿
04:33查看AI文稿AI文稿加 fx 等于一,加 x 平方分之三,也来个词,展开省,三次多项省。 那你不能说我没有积太的公式,所以我不会展开,没有这个说法啊。那三字太的公式,那无非就是 f 零加 f 一撇零, x 加二的分二的阶层呢?其实是二的阶层分至 f 两撇零,加三的阶层分至 f 三撇零呢?那不会就是一阶倒,二阶倒和三阶倒了, 对不对?所以这个没有,没有这个说法啊,大家不要不要以为这个他啊,不是我们的这个常用的公式就不去用啊,这是一个一种方法, 当然还有一种方法,这种方法就是另外一个问题了。什么问题呢?由于这里求极限的 人数啊,涉及有两项是和差的极限问题。那和差的极限我们能不能变成极限的和差呢?好,那么第二种方法,我就直接从原极限出发,把它改写成 x 距离 x 三字王分之他赢。三 x 加上 x, 三字王分之 x 乘以 fx 写成他。那么写成他以后,大家就要注意了,问题来了,什么呢?这一项的极限是不存在的, 因为分子等价于 x 等价于三 x, 三 x 跟他约掉是 x 平方分之三, x 平方分之三是区间于无穷大的,那你不能极限不存在,不存在,不能把它拆开。 哎,同样的要利用一个结论,什么结论呢?因为我们知道他用三 x 减去三 x 是等价于谁来三分之一三 x 的三字方的, 所以光取一个太难的词不行。那好,我剪掉一个三 x, 那当然这里就加上一个谁了,三 x, 那这样一来,原极限,哎,两个极限都存在了呀, 两个极限都存在了,那这样一个,第一个的极限应该是九,对吧?应该是九,那第二个的极限, 因为他总的极限要存在,所以第二个的极限肯定也是存在,因此就变成了阿哥斯 距离 x 的平方分值 f x 加三等于负九,那这样来,你就可以用, 比如说 f 零等于负三,用一下罗贝塔法则可以得到 f 一撇零等于零,再用,再本来不能用啊。嗯,用罗贝塔法则,对吧?罗贝塔法则可以得到他,然后再用二阶倒的第一, 二阶倒数的定义可以求得来 f 两撇零呢,等于负十八 啊,这样子的可以一样的可以解除啊。当然,当然,第一种方法显然比第二种方法要来得更直接,而且呢,更简单。 第二种方法你还知道要加一项剪一项凑一下才可以啊。所以第二种方法呢,用的稍微难一点。当然,我们同学有直接用两侧罗边的发色的 啊。有同学直接用两次罗贝拉,反正他也不管道理,他不讲道理,那硬个硬杠把他杠出来。 f 零等于零, f 一撇零等于 f 两撇零等于十八,这个就直接用的。对,他就是罗贝拉法则,一次不行,用两次。 那一个同学这么来做,那你这样做行不行?那没人说你,反正是个选择题吧,对吧,那你应该的也,反正别人也不知道你过程答案你做出来的。 但是呢,这样子显然对于你解题来说啊,这种方法是完全不可取啊,一定给出极限的题,一定是有一些别的技 技巧性的方法,除非罗贝达法则很简单,但是如果直接罗贝达法则去干的事情,一般都是高考的玩意,研究生入学考试肯定不会这么直接能把它杠出来 啊。所以呢,你们自己要多动动脑子啊,要想一想。这是第一题,第二题,引函数存在性定理。
 02:47查看AI文稿AI文稿
02:47查看AI文稿AI文稿超越特斯拉,干掉 bba, 你敢相信这是华为的高管亲口说出的话吗?华为虽然一直宣称自己不造车,但种种迹象表明,华为的野心比造车更大。华为虽然不造车,但从来没有停止过卖车。去年不造车的华为推出了三款车, 一个是和北汽推出的吉胡阿尔法 s, 一个是和小康股份推出的赛利斯 sf 五,还有一个叫问界爱慕。从这三款车身上能看到华为不断增长的野心。最开始呢,推出的是吉胡, 当时的华为还只是以智能驾驶解决方案供应商的角色出现,虽然后来几乎也出现在了华为的门店里,但是只展示不销售。后来到了赛利斯 sf 五,华为竟然开始在体验店里直接销售这款车,并且高薪高提成,招聘门店 销售人员,还制定销售目标。而到了第三款车,问戒 m 五身上就更离谱了,离谱到什么地步呢?离谱到在华为冬季旗舰新品发布会上,压轴的产品竟然不是华为自己的,而是这问戒 m 五! 问界 m 五是什么来头呢?和赛利斯 sf 五同中同源,都是来自小康股份,但却被华为拿到台上介绍了一个多小时。 发布会结束以后呢,展示区的问题, m 五的内饰上、充电桩上都写着华为俩字,好像这车就像华为造了一样。实际上这辆车呢,确实和前面两台完全不同。 问届 m 五虽然是小康股份造的,但是这是一台从头到尾都是华为主导的车型,从前期规划设计到营销,全部是华为包办, 而他的主人小康股份反倒像是华为的代工厂。发布会上,华为高管还夸下海口新车拥有百万豪车,外观内饰性能和体验参数上更是直接吊打 bba, 还要在二零二二年卖出三十万辆,华为哪来的信心呢? 这位高管是这样解释的,华为全国有五千家体验店,只需要启用其中一千家来卖车,每个店每个月卖三十台,哎,一个月就是三万台,一年三十万台不是梦。这个数据直逼在全球范围内有着极大影响力的特斯拉呀,特斯拉去年在国内的销量是 三十二万两,不知道你们怎么看?对华为的技术实力啊,我本人没有任何质疑,但是这个销售目标在我看来属实有些吹牛的嫌疑,不过这个呢, 还是要交给市场去验证。所以从这个角度来看,华为造不造车其实已经不重要了,因为目前来看,华为就是自己研发了一款车,找了个代工厂,贴上别人家的标在自己店里卖,结果说自己没造车,你信吗?
8.8万车事纪













