幂函数指数
粉丝1.8万获赞2.8万
相关视频
 01:37
01:37![[高中数学]幂函数 #高中数学 #高考数学 #幂函数 #高一数学](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/ad3fbb813d9ba2d0f4c64e016dcbc518~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2078960400&x-signature=Fuah31qr5KqYRzltSQxnLIoeTys%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=202511200901257DF9486CF0760A398F5D) 19:40查看AI文稿AI文稿
19:40查看AI文稿AI文稿大家好,今天我们继续来讲一下高中数学的密函数啊。密函数的话主要分成三个大点,你来看呗,第一点的话就是这个定义,第二点是图像性质,最后一点的话是一些常见的考点。先来看第一点这个定义啊,定义已经说的很清楚了, 一般的形容 y 等于 x 的 r 和次方,这个 r 呢,是一个常数,对于某一个确定的密函数来说, 然后这种形式呢,就成为密函数,然后 r 呢是一个长数,比如说,我们经常见的初中就学过的 x 的负一次方,实际上不就是 x 多少啊,不就是 x 分之一吗?反比的函数原来是一个特殊的密函数,包括这个 y 等于 x 平方,哎, 这是个什么函数?这是二次函数,实际上他也是一个特殊的密函数。当然啦,不是所有的二次函数都是密函数的,比如说你二次函数来个这个东西,加个二 x, 他就不是密函数了, 为什么不是呢?问题引出来了,很简单,因为蜜函数人家定义出来他的形式必须是纯粹的,因为蜜函数他是基本出等函数,就这个形式, 我们必须保证他前头这个系数是一系数是一啊,一乘了 x 的,你如果是二乘 x 的二次方,那就不是了啊。 然后底数 x 十四变量就是 y 关于 x 的函数,不是外关于 f 的函数,别搞错了啊,如果你写的是 y 等于二的 x 方,这个就这个就是之后学的这个指数函数了啊, 并且呢,指数是长数,是不变的一个数字啊。当然呢,有一个比较特殊的情况我还是要提一下的,比如说 y 等于 x 的零次方,任何数字的零次方都等于几?都等于一。当然了,咱们应该加一个括弧, 这个底数 x 不等于零,因为零的零次方在数学上没有意义,对吧?然后那你说 y 等于 x 的零次方和谁啊? 和这个 y 等于一,这个长数函数,也就是长函数,他俩能画等价吗?他俩能画等于号吗?其实不能画等价的符号,原因很简单,因为你第一行这样一个密函数呢?他默认底数是不能为零,但是人家这个长函数 x 随便取随便取,是不是啊?是这样一个道理。 那接下来我们就是继续来看呗。嗯,来看一个例题。这个例题的话当然很简单了,来看第一个是不是命函数。有同学说,老师,是啊,是啥呀?是啊, 他是经过密函数,经过平移以后左加右减吗?向右平移一个单位,他叫出导函数,不是基本基本出导函数。严格来说的话,你这么来理解,反正他哪个不服 不合呀?他的底数不是自变量,是自变量,经过改装以后,你 x 减什么?第一个不对的啊,第二个解释过了,叫指数函数啊,然后第三个,第三个不行,系数不是一吧,所以说一二三都不对。 第四个,第四个对不对?第四个也不对啊, y 等于 x 的依次方式对的, y 等于这个负 x 就不对了。西月书是正义,不是负义,只有第五对, 有没有就要说,老师你括号里头也经过改变了。我问你啊,这个 y 等于负, x 平方和 y 等于 x 方有区别吗?这两个完全能加,为什么?因为负负得正, 所以你既然外能用 x 方案是一个密函数,那外能负 x 扩注的平方负负得正,他也是个密函数,所以实际上只有第五个。只有第五个啊。继续往后来说,下边这个题的话是经常考的一类问题, 当然非常简单了。他第一个问的是什么时候取这个反比例函数?反比例函数,那你这个指数只能是负一吧, 因为是 x 分之 k, 那肯定就是相当于 k 乘 x 负一次方啊,所以这个 m 方减四, m 加三,这个指数整体呢,只能等于负一。那整理一下呗, m 方减四, m 加四挪过来了啊,那么左右两边同时加一以后,就变成这个样子,正好左边是一个 m 减二的完全平方的展开呀。所以说我们 m 只能取二了,所以第一个横向我们取二就可以了。第二个的话,他问的是当 m 取几的时候是密函数,密函数的话要求什么? 他实际上对于这个指数指数,你随便取备这个常数,但是这个系数你只能是几? m 方减三啊,只能是正好等于一的,所以说 m 方他只能是四, m 可以等于正负二两个数,你要让我写的话,我就正负二直接写上去了,对吧?第一个写二,第二个写正负二,然后你不信你自己验证一下啊,当这个 m 等于二的时候, y 等于 x 负一次方, x 分之一吧,它,当然它既是反比例函数,也是命函数。 然后看第二种情况,当这个 m 等于负二的时候,那不妨我们就带入验证一下啊,看他究竟算出来这个指数是多少。这算一下负二的话,这是,嗯 嗯,八加三,十一,十一加四,哦,十五次方,外等于 x 十五次方。当然对了,所以说咱们写对了啊, 那继续来看第三题吧。第三题的话,我们假设啊,他这个解题是肯定是写成这种 x 的 r 和次方,我就直接写上 x 的 a 次方吧。嗯,现在要求的就是这个 a 是多少,对不对?那好求啊,左边 加入这个点不就行了吗?加入啊,嗯,这个二十七的话,我们可以写成根号下啊,四四根号下,二十七 等于这个三的 a 次方。这个 a 是多少?不知道,显然这个二十七和三什么关系啊?有关系啊,那不就是三的三次方吗?四次刚好下三的三次方。哦,这个意思, 那实际上换一种写法就可以了啊。指数运算里头,我们直接写成四分之三次方。原来如此,原来如此,原来你这个 a 算出来是只能等于四分之三的,所以说我们这个结义是他只能写多少,他肯定就是 x 的四分之三次方,横向上写这个结果就可以了。 问题吧,继续来看第二点啊,第二点是重中之重,逆函数的图像性质,我们考虑把谁呢?把这个 y 等于 x, y 等于 x 分之一。其实第二个的话,你可以写成外等于 x 的负一次方,外等于 x 方,第三个啊,外等于,然后第四个的话,根号下,二次根号下,咱不妨写成 x 的二分之一次方嘛,这样才能更明显一些。我们把这几个呢,还有外等于 x 三次方,把这五个函数,五个都是密函数吧,放到同一个平面,这叫左标系中。 那此时的话,我们可以分析一下,有一些你其实是非常熟悉的,比如说外动用 x 的一次方,这个谁都知道,外动用 x 一次方,这是过远点的一条四十五度倾斜的直线,对吧?初中就学过。那,那外等于 x 分之一, x 负一次方呢? 过一三项线的两条什么两条双曲线吗?而且是关于这个圆点对称的。哎,是不是画出来了,然后外端 x 平方这个图像都知道,外端 x 三次方,外端根号下。嗯,然后有一个 需要注意一下,你说这个 y 等于根号下 x, 这个 x 怎么样啊?这个 x 只能大约等于零了,为什么?偶次根号下他这个自备量必须是非负的才有意义,对吧?你说根号下负一有意义,有这样的写法吗?没有啊,是不是?嗯,我们总结一下他这个规律吧。大概得总结一下在图像上啊, 当这个 a 大于零, a 大于零的话,实际上指的是什么?指的是他这个指数为正的时候,我们主要指的是谁呢?主的主要指的是 y 等于 x 呗, y 等于 x 平方呗, y 等于 x 二分之一, y 等于 x 三次方,那此时的话,肯定啊,随着 x 变大, y 肯定也要变道。所以说他在零到中穷啊,是单到低增,注意这个位置。人家是零的,什么区间啊?是包含零的。就是说自变量是 x 可以取零,但是如果 a 小于零, a 小于零的话,你不妨理解 y 等于 x 负一次方嘛,此时 x 作为分母,你说 x 还可以取零,你看这样一个细节里头画圈这个细节,这个自变量 x 他不能取谁了,他就不能取零了。而且此时他的单调性变成了在第一相间,在零到正规熊上单调 d 减了是不是? 那么还有最后一个我们发现呢?所有的密函数他都怎么样啊?他都在零到正无权上都有定义,实际上我们还可以说所有的这个密函数他在第一项下都有图像,你这么说也对,并且图像都过哪个点?都过一到一,为什么 乌海等于 x 的 r 和次方,当这个 x 取一的时候,一的任何词方,那不还是一,所以肯定过一的话,一这样一个定点,这是没有问题的。那看完这个图像以后,我建议你自己再画一画啊。那接下来我们就直接来总 截一下这个密函数的图像性质,主要是分成这三点都得掌握的啊。然后第一点就是当这个指数 r 他大于零的时候,那此时这个密函数 x 的 f 次方在零到中控上就是单调提升的,随着 x 增大和就增大了,并且这个位置你看 x 可以取到零吧,自变量里头原来包含零, 然后还要具体分,具体分的话就是你正数范围内还得跟一比较一下,如果你这个指数 r 和大于一,那第一项现在就是凹函数。什么叫凹函数呢?举个例子呗,比如说 y 等于 h 的平方,那此时这个二这个指数大于一吧。那第一项现在这个图像你看向下凸起来,向下凸起来,那不就凹的意思吗?这叫凹函数啊。那什么叫凸函数呢?比如说 y 等于根号 x, 看图中这样一个绿色的线,图中这条绿线向上凸,那就叫凸函数,这个明白了吧? 好,这就是凹函数和凸函数,咱们都已经说了,那么还有,难道这个阿尔法他怎么样?他不能小于零啊? 当这个 r 和小于零的时候,在第一项现在是怎么样的?在第一项现在是单调第一减的,然后当 r 和为零的时候,刚才其实咱们第二点也总结过,说过了啊,它实际上相当于 y 等于一,这样一个长寿函数,去掉了哪个点, 去掉了 x 等于零,就是跟外中那个焦点,那个焦点这个位置应该画空心,懂了吧?就这样一个含义。那么有的人说了, 老师你刚才画的这些图都是说在第一项,现在怎么怎么样?在零到中无穷上,嗯,那你说这个富无穷到零上,咱们就不画了不是?所以第四步的话,咱们只需要根据什么? 只需要根据这个机油性把这个第一项现在的图像究竟是根据外轴对称呢?还是根据远点对称?对称过来对吧?饥寒数,你就关于远点对称一下, 然后偶函数呢,你就关于外轴,把谁对称过来,把这个外轴右侧的对称到外轴左边来就行了。所以说嘛,如果你真的想很快的画出这样的密函数的图像,有的时候解决很方便的啊,那需要分几步? 分四步,咱们以谁为例?就不妨以这个 x 三分之二次方这样一个命函数为例,显然外等于 x 三分之二次方,我们可以写成三字根号下 x 的平方。哦,写成这个含义了,先看第一步就能定于 这个定义怎么样?因为 x 什么?因为你这个 r 和三分之二才能取正数。其实你就看后边这个式子,更容易看出来,不管我 x 随便怎么取,他都有意义。所以说定义是 r v。 好,先确定定义第一步。第二步呢?先确定在零到中控程度上,第一象限的 单调递增还是单调递减?这显然随着 x 增大外要增大,所以是单调递增,而且是向上凸的,这样一个凸函数就增长越来越慢的意思啊,你知道这样一个含义就行。 那最终的话,我们要看什么了?第四步就要看这个基友性了,基友性的话,因为它里头有个平方,嗯,随便举个例子嘛,比如说当这个 x 取正义的时候,那就是一的平方, 那当这个 x 取啊,负一的时候,负一平方,其实他俩是等价的,是可以画等于号的。也就是说当 x, 当自变量互为相反数的时候,这两个函数值相当,你说是不是偶函数?是偶函数?偶函数的话,我们只需要根据第三点 一向前你的图像,然后干嘛关于外出对称过来,完整的图像就画出来了,就是最下边这样一个图像,懂了吧?分四步,第一步定义,第二步单调性。 第三步怎么样啊?第三步,咱们只需要画出第一项线,然后第四步根据这个记录性把整个图像补全就可以了,这就是步骤。那了解了这样一个步骤有什么好处呢?咱们看一下啊。 先来看第一道,第一道很简单,这个题目,嗯,显然他让你选择为,哦,第一项,现在单调递减啊,第一项,现在单调递减,那就只能是什么图像了,那就只能是这个指数 r 的小于一,小于零啊,小于零的话,所以说 c 四对应的那只能是负一了,对吧? x 负一次方, 嗯,显然那条线非常特殊啊,还有一条直线嘛。 c 二是一条直线,那只能是 y 等于 x 的一次方啊,这指数是一, 嗯,然后继续。这个是什么呀?哎呦,这个显然是 y 等于 x 平方吧,是个凹函数吧。所以说这个 c 一呢写二。 哎,那这个 c 三的话,是一个凸函数吧,凸函数增长越来越慢,那只能是根号 x 或者 x 到二分之一次方,所以他的指数是二分之一,你横向按这样的顺序写出来就行了。 那继续来看第二题。第二题的话,他说以下函数中,首先得过零的话,零一的话,一肯定过。因为以下这几个图像,这几个函数呢,都是密函数,不用验证了。所以接下来我们只需要验证这个图像过零的话,零和偶函数这两点就够。 零多少?零的话, a、 c、 d 都过零的话,零啊, b 为什么不过呢? b 的话,你写成 y 等于 x 方分之一,那肯定 x 不能是零,他不过远点的啊,远点就没有图像了。那 a、 c、 d 究竟选哪个呢?哎呦,偶函数,偶函数。先看第一个, 第一个他既不是记函数,也不是偶函数,因为你这样一个函数,只有 x 大于等于零,只有外轴右侧的定义率, 地狱都不是官员的对称,那既有性何来的讨论呢?看这一点,这一点,哎呀,直接选 c 就行了, d 为什么不行啊?因为 d 是一个极函数。嗯,第三点, 第三点的话,他是这么说的啊。首先他跟这个 x 轴外轴都没有公共点。有人 就要这样说了,老师,没有公共点意思,就是说不过零的话,零的意思,所以呢,就这么写了。老师,这两个指数啊,这个 m 减六,这个指数呢,只需要它是复数,然后二减 m, 这个指数呢,这两个指数为复数就可以。其实不然, 为什么?因为 y 等于 x 的零次方。人家图像是怎么画的呀?人家图像是,哎呦,中间这个点, y 等于一去掉了外轴上这个点,你说他跟这个外轴 x 轴有焦点吗?其实是都没有焦点,所以你说这个指数能不能是 x 的零次方指数可以是零, 所以这俩位置呢,带上等于号,那带完等于号以后,我们所以就求出来了,这个 m 呢,是大于等于二,小于等于六的。那究竟哪个合适,哪个不合适?你意思再代入不就行了吗? 那相当于这个 m 减二,他必须在零到四之间,零一二三四,一共五个数字,哪个数字行,哪个数字不行。你一定要注意的是,人家是关于外出的人, 所以说嘛,这个 m 减二,他只能是偶数了, m 减二是偶数,是,那就相当于 m 是偶数,你说二到六 m 有几个偶数啊?所以说嘛,二 三三不行,二四六吧,所以 m 等于二四六,这三个数都有可能,你分别写上就可以了。终于讲到第三点了,第三点的话就是一些考点常见的跟单调性不等式综合的题目,咱们来做几道啊?来看这个第一题, 第一他说呢是个偶函数。嗯,然后最后问题里头也很关键,他说整数 a 是整数的话,你经过这样的运算,所以这个整体 a 方减四 a, 然后再减去九呢?他也是什么数啊?他也是整数,整数要求是偶函数,所以这个 a 方减四, a 减九,基数行不行?基数肯定不行,所以他必须是偶数,偶数里边的整数,整数里边的偶数,懂了吧?必须是偶数。 嗯,那既然是偶数的话,我们改一下形式,这个 a 方减四, a 减九,那为啥不给他凑一个四呢? 原因很简单,首先啊,这九的话就写成了四减多少,负九写成了四减十三的形式,没问题。为什么要凑这个四呢?凑成完全平方的展开形式吗?也就是变成了 a 减二的平 方减十三。好嘛,这个意思,我们要要求这个整体是偶数,哎,十三是基数吧,谁减基数是一个偶数啊?哦,懂了,那必须保证这个 a 减二的平方是基数, a 减二的平方。注意啊, a 是什么? a 是整数, a 减二,它实际上也是一个整数,整数里边既分基数又分偶数,没有别的喇叭。 所以接下来你考告诉我,你说这个 a 减二,这个整体应该是什么数啊? a 减二,这个整体,我们只需要保证它是基数就可以了, 为什么?原因很简单,基数的平方还是基数,偶数的平方呢?就变成偶数了,对不对?所以你说这个 a 的值他应该取多少啊?非常好说,只需要再满足第二个要求,人家要求什么?人家第二个要求还要求他在领到中 从上是减。哎呦,是减还是?我不就是告诉你 a 方减四, a 减九小于零吗?小于零的话,这个是很容易推的啊,我们最终的话会得出这样一个十字来,也就是说 a 是在多少之间啊?在这个二减根号十三和二加根号十三, 这个根号十三是在几到几之间,是在三到四之间的,所以这个后边就好说了,那不就是负一二再加上三,那就是小于等于五,你应该知道什么意思了吧? a 减二都是基数了,那 a 我们要求也必须是基数,你说负一到五之间究竟有几个基数啊? 负一是基数啊,横先生啊,然后零不是吧,一是吧啊,然后三也是吧?胡也说,所以说只有负一一三五这四个答案。继续来看第二题啊,第二题的话,他首先要求 这个是 g 函数,并且要求在这个复活穷到零上单调 d 减,这一看 a 就对了嘛,因为 a 是什么? a 是反比 b 函数,一看就对啊。我们来看这个下一个跟不等式综合的题目。 这不等式综合的题目呢?实际上,你不管是 y 等于 x 四分之一,还是下一道题 y 等于 x 的这个二分之一次方,这两个函数的草图都是长得非常像的啊,它只在第一项,现在有图像,当然也是过远点的,它还是一个向上凸的函数,对吧? y 等于根号下 x 啊,或者四字根号下 x。 那既然如此的话,我们先来看这个第一题。 第一题看一看。哦,我知道了,首先你的定义率是零到正无穷,那我这个不等式里头除了要满足在第一项,现在单调一增 x 减六这个整体小于 x 之外,还得大于等于零,是不是?我们先解第一个啊,第一个的话,不就是 x 方大于等于六吗?再继续往后减, 那就相当于 x, 他必须在什么方向内负无穷到这个负的根号六 在并上,根号六到正无穷,这是第一行,还得满足什么?哎呦,你还得满足这个 x 方减六小于 x, 我移向了啊,减 x 减六小于零,这个的话很容易硬是分解,我就直接硬是分解了 他。一是分解之后的话相当于 x 减三,再乘 x 加二,然后小于零,小于零的话,不就相当于这个 x 是在什么范围内? x 是在负二到三这个范围内的。 负二到三的话,首先你告诉我负根号六和负二哪个小哪个大?哎呦,肯定是负二大一些,所以说没有,但是,哎,根号六和三根号六比三要小。所以说嘛,你这个答案是根号六到三的左臂右开,这是第一个答案。 然后第二个题的话就也好做了啊。第二个题我们就直接写了,它相当于二 x 减一,因为是个单调增长的数码, 小于三 x, 然后还得大于等于零。先解第一个不等式,这个很快就算出来 x 大于等于二分之一了,再解第二个不等式,第二个不等式算出来 x 大于负一倍,且的关系取交及。 所以说第二个横线上我们要写的范围就是 x 大于等于二分之一。当然你写机会也对啊。分享上知识,感受数学之美。我是安范老师,下节课再见。
1.6万会放羊的教书匠 16:11
16:11 00:16
00:16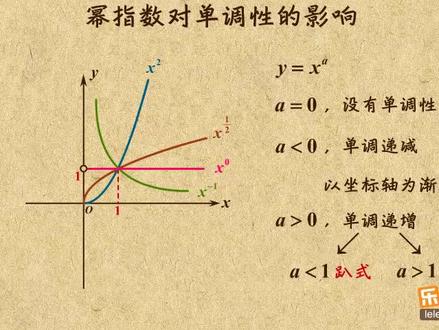 03:26查看AI文稿AI文稿
03:26查看AI文稿AI文稿前面咱们画过了密函数图像,所有的密函数在第一象限都有图像,这个视频咱们就来专门看一下这个区域内密函数图像的单调性。 a 等于零时,他的完整图像是 y 等于一这条直线去掉这个点,那就没有单调性。 a 小于零时,比如 x 到负一次方,也就是 x 分之一,他的图像在第一上限单调递减,指数换成其他复数也一样都有。 x 越大, y 就越小,并且指数小于零,则定律不含零,那图像跟 y 轴就没有交点,而是以它为间接线, 而 x 不等于零,显然 y 也不可能等于零,所以图像跟 xo 也没有焦点,而是以它为尖尖线。总的来说,当指数小于零时,密函数在第一象线单调递减,并且图像一座 标轴为间接线,没有焦点。从前面的过程你已经知道,在第一项线内,指数等于零时,函数没有单调性,而指数小于零时,函数就递减。那如果指数大于零又是啥样呢? 还是挑选几个代表来看看吧。指数为二长这样,指数为一,长这样,而指数为二分之一就长这样, 他们都过远点,并且 x 越大, y 就越大,所以在第一项线内函数递增。以上就是密函数的单调性跟指数之间的关系。学了这三招,随便给你个密函数,你都能轻松判断他的单调性。 那如果反过来告诉你一个密函数的单调性,你能算出指数中的参数吗?比如以之外等于 x 的 m 方减六 m 加八次方,这个函数在开区间零到正无穷上单调递减,求 m 的取值范围。前面咱们说过,密函数的第四项线都没有图像,那在开区间零到正无穷上的图像就一定是在第一项线函数递减,那指数就必须得小于零,也就是 m 方减六, m 加八小于零。记得 m 大于二小于四。搞定 一只单调性的题目,你会算了。那如果没说单调性,而是告诉你,这个函数的图像跟坐标轴没有焦点, m 该咋算呢?前面咱们说过,密指数小于零,图像与坐标轴没焦点,那 m 的范围就还是大于二小于四吗? no! 千万别忘了,指数等于零十,他跟坐标轴也是没有交点的,那就是说要求 m 的范围这个小于号得改成小于等于号解得 m 大于等于二,小于等于四。好了,指数的正负性对函数单调性的影响讲差。 最后我再给你补充一下指数大于零时,图像增长的两种趋势,发现没,指数为二十,图像增长越来越快,而指数为二分之一,图像增长是越来越慢的。其实只要指数大于零小于一,图像就是这样, 就像一个不满一岁的孩子只会趴着一样,咱们叫他趴式图像,而指数大于一时,图像就长这样,就像一个一岁以上的孩子慢慢会站起来了,咱们叫他立式图像。有了这俩名字,你就能轻松记住他们的画法了。 好了,又到了总结时间,这个视频我主要给你讲了,密函数在第一项线内的单调性,指数为零时,没有单调性,指数小于零,单调递减,并且以坐标轴为尖尖线。 而指数大于零时,函数地增地增分两种,小于一为 pass, 大于一为历史。怎么样,明白了吗?明白了就赶紧刷题去吧。
180在线学习高中部
猜你喜欢
最新视频
- 2.8万张小知













