tanx导函数
粉丝1.0万获赞56.5万
相关视频
 01:48查看AI文稿AI文稿
01:48查看AI文稿AI文稿r q 弹肩 tx 的导数是什么? r q 弹肩 tx 的导数是一加 x 平方分之一。 因为反函数的导数等于圆函数导数的倒数, 所以咱们要找摊间 tx 反函数的导数,也就要先找到原函数的导数。所以咱们可以设 y 等于 rq 弹间 tx, 那么 x 就等于摊间梯外,因为摊间梯外的倒数也就等于了三以外除以扣三以外的倒数,然后再利用倒数的除法法则,咱们就 得到扣三引平方歪,再分针三引歪的导数,也就是扣三引歪,再乘以扣三引歪,也就是扣三引平方歪,然后再减去 三引歪乘口三引歪的导数,也就是加上三引平方歪,进一步化解,就变成了一加上摊间梯平方歪, 而这里的弹箭体 y 也就等于 x, 所以这里就是一加上 x 平方。那么因此 rq 弹肩体 x 的导数也就等于弹肩体外的导数再分之一,也就等于了一加上 x 平方分之一。有看懂吗?我是罗老师,关注我,咱们下期再见。
753罗姐数学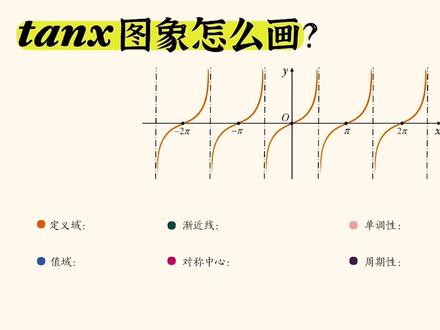 07:40查看AI文稿AI文稿
07:40查看AI文稿AI文稿sign 扣伞咱都学好了,那 tangent 怎么画呀?这个我不给大家一点一点描点了哈,我直接把图像拍给大家。 tangent 它本身也是一段儿段儿的周期函数,因为很简单,咱们这角度啊, 是任意取值的,我只要转一圈它的性质,它的图像就会循环往复的出现,最后通过列表秒点连线。 tanden 怎么画嘞? 他在一个固定区间上,一直一直是一个增函数,由负到正,关键是这两个端点分别是谁? 他左右有两条渐进线,第一个渐进线是负二分之判,第二条渐进线左右对称的是二分之判。他这个函数值啊,他会无限趋近于正无穷,但是他绝对这个图像跟渐进线是没有交 高点的。为什么?贪婪的怎么能正无穷类?大家想,当这个角无限接近二分之派的时候,当这条角的中边咱怎么画嘞?无限接近于 y 轴,那这个时候他的纵坐标那肯定无限趋近于一, 横坐标肯定无限趋近于零,它无限接近零一点。那 tangent 咋定义的来着? tangent 是 y 零比 x 零。 那咱这分子无限趋近于分母,无限趋近于零。哎,分母能取零吗?不能取零,所以他才会有这个渐进线, 他才取不到二分之派。而且当他无限趋近于二分之派的时候,你想嘛,分子是零点九九九九九九九,无限趋近于一分母,无限趋于零,我就取零点零零零零零零零零零零一,这一除完,这个值会 相当相当大,最后趋近于整无穷。这就是我们对 tangent x 这个图像非常直观的一个理解。从负二分之派到二分之派,就是他整个图像的一个基本单元, 咱可以通过把这一段平移平移得到下一段啊。那每一段他的这个周期是多少啊? 注意哦,看着 x 周期,我带着这个轴一起平移,大家可能会更直观一点,他平移多少是下一个周期嘞?我只要看两个对称轴之间的距离是不就可以了呀?两个对称轴之间距离,很显然,一个负二分之派,一个正二分之派,距离是派,他的最小正周期 等于派。它的定义非常关键。是属于 r 吗? x 有没有一些点它取不到啊?你看这个点,这个点它都取到了没啊?凡是见 近线的位置,他都取不到。其中一条渐进线是二分之派,咱写出来如何用一条渐进线表示出其他渐进线?他具有周期性的,每条渐进线距离是一样的,距离是 pa, 我就加 k pa, 这就是渐进线的表达方式。渐进线写完了,定于预,自然而然就有喽。 x 取不到间接线, x 就不能取 k 牌加二分之牌?这俩最难写的都写完了,别的就简单了。值欲,值欲是啥?他从最低点负无求到最后高点正无穷,值欲属于二 对称中心。怎么求?看好哪是对称中心啊,同学们比较容易找得到的。零啊,派啊,二派啊,副派啊,这些个整数点肯定是对称中心,但是同学们容易落掉的。其实他还有一个对称中心,你看这个点,整个图像也是关于二 二分之派对称的,你看二分之派左侧,哎,这么画,右侧,这么画,关于他一百八十度对称不对称,然后我左边往下,右边往上,对称不?还对称,每一个对应点都关于他对称,你看左边低,右边高, 左边高右边低。因此我发现所有的整数倍的派以及二分之几派,二分之一派,二分之三派,二分之五派,负二分之一负二分之三,负二分之五,全都是对肾中心。最后呢,我就用二分之 k 派来表示了, k 属于 c, k 是基数的时候,代表着所有的二分之基数点,反过来, k 如果缺偶数,代表所有的整数点。你想二分之二就是一,二分之四就是二,所以相当于把零啊, 派呀,二派呀也全都囊括在内了。最后,单调性,单调性这个考的比较少了,这很显然,看着耐克就是从负二分之派到二分之派一直单调递增的呗。别的区间我懒得写了,大家就记住他在对应的负二分之派到二分之派之内是一个增函数就够了。 图像都绘画了,题怎么做呀?最简单的题目,看图说话。他问我哪个是对称中心,我就看呗。刚才都说了,所有的二分之几几派都是对称中心,那哪个是二分之几派?这四分之的肯定不对,只有 d 选项对,选上结束。 接下来给我一个函数,问我,定域。哎,定域?啥是定域?他有对数,那帧数位置得大于零, tandent x 减一大于零呢? tandent 就得大于一,哪儿是探证大于一?一在哪啊?一, 在这,咱取函数值比一大的区域。那截完的图像,那就是这一段,这一段,这一段,他每一段距离都是类似的,每段距离全都相等的,等于几类,应该是一整个周期。是派啊, 所以你会发现最后他这个答案啊,肯定加 k pad 是对的啊,你看是不是每一项都加了 k pad 哦,没问题。那关键是啥呀?咱只要把其中任何一段他的取值范围找到是不就行了呀?首先左短点,咱把图放大, 这只是几,相当于问大家滩镇的多少度是一滩镇的四十五度是一四十五度,其实就是四分之派嘛。右端点他无限哎,无限往上走,是不是?所以他就无限趋近于渐进线了吧。渐进线是多少来着?应该是二分之派啊,所以其中一段 我就直接写出来了,是四分之拍到二分之拍之内。写完一段怎么写别的段?咱把它简单的往右拼一拍,往左拼一拍,拼一拍,拼二拍啊,拼一副拍啊,拼一副,二拍评一整数倍的拍,在原来的基础上都加 k 拍就行了。所以谁是答案只能选 d。 又是具有周期性函数的,看图说话,有周期性我不怕,我先把一段画出来,然后再把它直接平移,平移平移就可以了,找其中一段,再找不同段之间的距离,就能完美完成任务。 接下来啊,再来,他问我一个新函数,这新函数,哎,取个绝对值,他问我周期是多少?小笨蛋,这我看都看出来了,怎么叫取绝对值啊?上方的图形不动,下方图形原本是这么画,我把它翻上来, 所以相当于问我这一个一个的小优字型,他的周期是多少?这周期我把它往右平移,再往右平移,这周期你看最低点。最低点是怎么是在这个点往右平移到这个点最低点间距离多少啊? 从这到这,这是零,这是负二分之派,这应该是负派距离,我这么一算,他是派,那这段距离就是周期,所以直接选 b。 做了这么多题,说白了就干一件事就是画图。图像是解决几乎所有函数问题的最核心方法,这函数只要能画图,无论是难题还是简单题,都是看图说话。那有关三角函数综合难题,我们将在未来给大家详细讲解,晚结 滑。
510神奇小猪 01:28查看AI文稿AI文稿
01:28查看AI文稿AI文稿大家好,我是罗老师,贪奸 tx 平方的导数是什么?贪奸 tx 平方的导数等于二 x 加上二 x 乘贪奸 t 平方 x 的平方。 好,他这个是怎么来的呢?首先我们需要啊去设 y 等于摊间 tx 的平方, 很明显他就是一个符合函数了,对吧?所以我们就要想到换元法,咱们就用 u 等于 x 的平方,然后外呢,他就等于摊间 t u, 然后这个 u 的导数他就等于二 x, 那 y 的导,也就是啊,摊间 t u 的导数呢,他就等于一加上摊间 t u 的平方好,然后这个 u 我们用的是一个换元法, 所以说这个时候你是不是得还原,也就是一加上摊间贴啊 x 平方啊,这里还有个平方, 好,所以摊间梯 x 平方,他的倒数就等于二 x 括号,一加上摊间梯平方 x 平方, 然后用乘法的这个分配率展开,咱们就得到了二 x 加上二 x 摊间贴平方 x 平方啊,这就是他的一个推倒过程,有看懂吗?我是罗老师,关注我,咱们下期再见。
40罗姐数学 03:01查看AI文稿AI文稿
03:01查看AI文稿AI文稿正切函数求导有很多种方法,比如定义法,比如图像法,就是画个单位元,比如利用反函数的性质,他的 tenax 互为反函数,用这个性质进行求导。还有很多种特殊方法, 我这里介绍最简单的一种利用法术的性质,就是更太难克死,会反术进行求导。 由于 y 等于 x, 太监特,可以写着 x 等于太监特 y, 他会反函数吗?那对于这个东西进行求导, 关于 x 进行的 a 求导,等于一胎的外求导。由于是关于 x 进行求导,所以这车上有一个负荷函数,外表是个胎心的外,内部是个 y 归于 x 的函数 特点特 y 的倒数等于 s e c 的平方。 s e c 是什么东西呢? s e c 可以看看做 s e c x, y 等于 cos and 倒数, cos and 的倒数。这定义啊,好,那么求求到啊,这一步, 他进的的导数等于他外的导数就他本身。 然后我们把我们需要的这个导数是外我们需要的导数吗?放到一边,摄像头放到另外一边 转换,我们把这个 s, c, c 不常见的 s, e, c, 背着我们平常常见的靠山 就转变为 y 等的导数,就用这个函数的导导数等于 coseyy 的平方。到这一步之后,我们要考一 coseyy, 把转换成 x, 那怎么转换呢?用这个 tantoy 等于 x, 我们想要把 tantoy costly 表示,然后进行一个计划,我们想想,我试一下吧, china, y 等于他,他平方等于三十平方加 co 三的平方。由于三十平方加 co 三等于一,可以把三十平方 换成一点 cosen 平方。由于 ten y 等于 x, 所以他等于 x 的平方,然后就 cosen 的平方 y 等于一加 x 平方,方分之一好,等于倒数就求出来了。
 02:03查看AI文稿AI文稿
02:03查看AI文稿AI文稿r q 探监 tx 的导数 r q 探监 t x 的导数是一加 x 平方分之一。 那首先我们需要知道反函数的导数等于原函数导数的倒数,所以我们要求摊间 tx 反函数的导数也就要先找到原函数的导数。因此我们可以设 y 等于 r q 弹肩 tx, 那么 x 就等于弹肩 ty, 也就说明这个摊间题外就是二口摊间题 x 的原函数,而摊间题外又等于三以外,除以口三以外,所以摊间 py 的导数就为三引 y 除以扣三以外的导数。然后根据导数的除法法则,咱们就由扣三以平方 y 再分着三以外的导数乘以扣三以外,减去三以外乘以扣三以外的导数, 而三以 y 的倒数等于扣三以外,而扣三以外的倒数等于负三以外, 所以这个地方的分子就变成了扣三影平方歪,加上三影平方歪,再除以扣三影平方歪,然后分子分母同除以扣三影平方歪。那么这里的结果就变成了一加上 摊间梯平方外,然后因为这里的摊间梯外呢又等于 x, 所以我们还原也就是一加上 x 平方,所以 r q 盘减体 x 的倒数也就等于了一加上 x 平方分之一。有看懂吗?我是罗老师,关注我,咱们下期再见。
117罗姐数学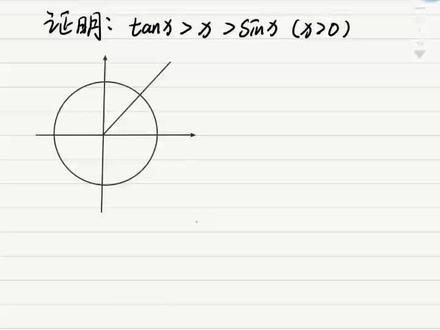 05:20查看AI文稿AI文稿
05:20查看AI文稿AI文稿这个视频带大家一起来证明一下,潘建的 x 为什么大于 x, 大于 six? 首先我们要画一个单位元,然后假如有一个角为 x, 他的中边与我们的单位员相交于点, p 过点 p 做 x 轴的垂线,假如垂足为 bx, 轴与单位原相交的点为点 a 过 a 点做这一个 x 中边的垂线,垂足假如为 m 点,那么这个呢,就是利用我们的三角函数线,很显然啊,我们都知道了是 三角形 opb, 三角形 oma 都是直角三角形,那么所以在直角三角形当中啊,很显然, 我们的赛营 x 就等于在三角形 opb 当中,赛营 x 就等于我们的 pb 比上 op, 而这个元是单位元,单位元,那么他的半径就等于一,所以说这一个长度最终化减出来,就等于我们的 pb 比上一,也就是等于我们的 pb 就是我们的三元 x, 而我们的 tend x 呢, 我们需要把它放在我们的三角形 oma 当中去, oma 当中去 tiendx 等于我们的对比零, 对比零就等于我们的 am 比上 oa, 而 oa 又等于,所以啊,这一个式子化减下来就等于我们的 am。 所以说,我们可以知道 的是,在这一个元当中,三年 x 就等于我们 pb 这条线段的长度,而 tinjinx 就等于我们的 am 这段长度。那么很显然啊,我们可以得出的是,在这个三角形当中,很显然我们的 am 是大于 pb 的,对吧?所以说我们的 tinjinx 大于三 x 的。 那么在图当中呢,我们要去观察一条线,那就是 xx 等于谁?根据我们弧度制的定义,弧度制的定义就是我们的弧长与半径的笔直就是我们的弧度制,所以啊,在这个图当中,那么我们的 x 就很显然是等于我们的 pa 这段弧长比上我们的半径 r, 而我们的 r 等于一,所以它就等于我们的 pa 这一段弧长。那么很显然我们要晓得的就是,为什么摊件的 x 要大于我们的 xx 呢?要大于我们的三 x, 那我们现在思考一下,摊件 x 也就需要证明我们的 am 是大于 pa 的, 我们现在需要证明的是 am 这条线是大于 pa 这个弧长,那么要证明 am 这条线大于 pa 这个弧长。所以我们需要看两个图形,第一个图形就是我们的 rt, 三角形 oma 以及我们的这个扇形 扇形 opa, 从图当中我们不难观察的出啊,三角形 oam 和扇形 opb 的面积谁大谁小,那么很显然就是我们的 s 三角形 oma 肯定是大于我们的扇形 opa, 因为这里多出了这一块,对吧?所以说这个是我们需要去把三角形 oma 和扇形 opa 的面积给表出来,很显然我们就知道了,三角形 oma 的面积等于我们的二分之一倍 am 的线段长度再乘以我们 oa 的长度,那么上一些的面积呢,是等于我们的二分之一倍 l r 的,那所以说这个 地方又变成我们的二分之一倍 am 乘以一,这个扇形的面积等于我们的二分之一倍 l 等于 pa 这段弧长二等于好多一, 那么既然他是大于他的,对吧?那么他大于他,那给我们约个分二分之一,二分之一约掉,这,所以最终得出的结论就是我们的 am 大于 pa 这一段弧长 am 大于 pa 这段故障,那么所以也就可以推出的就是我们的探见他 x 是大于 x 的,所以我们就可以推出的是我们的探见 x 大于 x。 那么很显然呀,这一个曲线 pa 这一段弧长,它很显然是大于 pb 这条垂线的长度的,所以我们的 x 就大于我们的三 x。 那么综上我们就证明出了贪健的 x 是大于 x, 大于 赛英 x。 那么这个结论啊,同学们一定要掌握在我们的后面的学习过程当中,可以直接拿出来用。
652小曹数学 02:20查看AI文稿AI文稿
02:20查看AI文稿AI文稿欢迎来到每日一讲,今天我们讲一道不定几分的计算题。好,我们一起来看一下, 中间这个函数是摊件 x 啊,那我们就想想不定积分的公式里面有没有一个函数啊,他求完导之后为摊件 tx 啊,是没有的哈。啊,没有的话,那就不能直接根据公式走出来他的原函数啊,那就换一个方法, tint x 的话啊,可以根据三角函数给它展开。好,把 tintint x 展开为三 e x, 除上括三 e x。 好,那现在啊,这个计算就变成了分式了,分式的话,我们可以把它转换成两个函数相乘。 好,两个函数相乘的话,有两个方法可以选择了,侧尾分和分布积分啊。首先考虑啊,能不能用侧尾分,那就看三印和括三印他们的啊之间有没有导数关系。 三 e x 啊,它求完导为括三 e x, 括三 e x, 求完导为负的三 e x 啊,这两个函数之间有导数关系啊,有导数关系的话可以用车尾分, 我们需要把其中的一个函数还原成导数的形式。好,这个 q 三 x 在分母啊,三 e x 的话,它就是一个整体啊,在外边的啊,那我们要还原的话,就还原这个啊,还原这个三 e x, 待会还原成这一个啊, call 三 e x 的话,不太好算啊,还原三 e x, 把它还原成导数的形式。那哪一个函数求完 倒为三 e x 呀,是负的。括三 e x。 负号的话,提到积分符号最前面去。 好,下一步的话,就是需要把 cosine 的导移到 d 后面去,甩掉导数符号, 好,最后一步的话,又用到整体画圆的思想。把扩三 e x 看成框的话,那就相当于是计算框分之一地框,计算框分之一地框的话, 计算出来就为 non 框的绝对值加 c。
 05:29查看AI文稿AI文稿
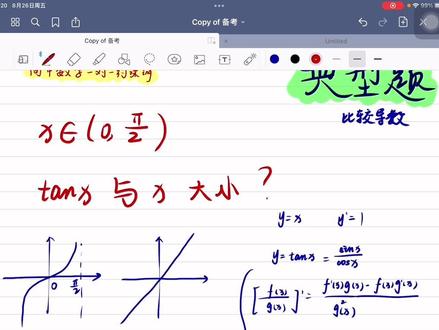
05:29查看AI文稿AI文稿我们今天来看零属于二分之派的,开车间的时候摊田 x 和 x 大小比较哈,但是我们知道,嗯,这个摊田 x, 他的图像是这样样子,这样样的,这样的,差点方言都出来了。摊田 x 零到二分之派嘛,对吧?嗯,然后这个 y 等于 x 这样的对吧?你不知道图像谁高谁低,你现在没放到一块去看啊?没放到一块去看,你根本不知道图像谁高谁低,那怎么办?哎,比较摊田 x 和 x 大小的时候,咱们比较倒数就好了。宝宝们啊, y 等于 x 的倒数, ypr 是不等于一呀? 等于一就是它的增长速度就是一匀速的,匀速增长的。那这个 tantianx 的导数 y 等于 tantianx 的导数。有没有背过?有背过的吗?有背过的直接用就好, 没有背过的话我带你去求餐厅。 x, 他不等于三年 x 比上扣三 x 吗?宝宝们,挣钱函数等于挣钱函数比上余钱函数,然后求歪撇的时候不就是,嗯,把它看成那种 fx 比上 gx 整体的一倒就等于 gx 的平平方, 然后上倒下不倒前去,上不倒下倒,对不对? 就是求,就按照他这个方法去求咱们三 x b q c x 导数就好了。三 x 的导数和 q c x 导数你再没有背过的话,那我真的没有办法了,宝贝,咱至少也得记住一些吧, 是不是啊?记住一下啊,三 x 的倒数是扣三 x, 扣三 x 的倒数是负的,三 i x 分三 x ok, 然后我们就求这个外皮,这个外皮的话就等于这个 扣三 x 分母吗?平方,然后上倒下不倒,上倒是扣三 x 下不倒是,还是乘扣三 x 减去上不倒上不倒不是三 x 吗?下倒下倒是。是 qcx 吗? qcx 倒完之后是副的 cx, 所以他得再成一个副的 cx, 我别跳步了哈,宝宝们,因为我怕有的基础不太好,所以跟不上 成一个富的三 x, 真的有基础不太好的宝宝在看我的视频哈,我不能总是为了迁就那些基础好的我咔咔一顿跳步,那这样的跳下来最后我也没什么粉丝了,因为毕竟基础不太好的宝宝们占大多数哈,要为大家考虑。嗯,然后就等于 于,上面就是扣现 x 平方对不?宝宝们,加上 cx 平方对不?宝宝们,用归一公示。啥是归一公式啊?我也不知道这个名我从哪学来的好宝宝们,我某次看一个教辅资料的时候学到的, 三亚 x 平方加 cocyx 平方等于一,这个公式就叫归一公式哈,咱以后就就这么称呼他。然后这样的话上面就是一底下呢是 cocyx 的平方对不对?宝宝们,对吧? 然后,呃,你们跟着我看啥呀?宝宝们,你给我看 coatx 在零到二分之派的时候,他的大小范围,我想让大家看看这个歪皮 就是,呃,咱不是比较变化速率吗?咱们这个 y 等于 x 的变化速率是匀速的,是定制一,然后这个 y 等于探天, x 的变化速率是不匀速的,但是他他跟一比较大小的话很好比较。为什么呢? x 属于零 到二分之派的时候,咱们的 qcx 你看看,是这样的,是属于。嗯,这两部曲哈,是属于零到一的,就 cocyx 属于零到一。那 qcx 方也属于零到一啊,宝宝们 也属于领导一,那扣线 x 方分之一属于多少?哎,有的同学说也是领导一加上分之一,你要不会判断的话,宝贝你就画出来反比例还输图像吗?不就是 零到一的时候,你就把这个扣进 x 的平方看成 t, t 是属于零到一的,然后看看 t 分之一是属于啥的,你看多么的明了啊,我讲题是不是老清楚了, 真的,我真的有时候自己挺佩服自己的,看,我们零到一的时候, t 是属于零到一, t 分之一就是 一的时候不正好对应的点是这个一吗?一的时候对应的点是这个一,零到一的时候就是哎哎哎哎这一点。所以 t 分之一应该是从一到正无穷,所以咱们的扣现 x 分之一是属于一到正无穷的。 知道正无穷是一定大于一的不?也就是说贪铁 x 的这个导数是大于一的,然后原来这个导数是上面这个外地为 x 的导数正好是一,所以贪铁的这个导数是大于 y 等于 x 这个导数的。啥意思?咱俩都在增,但是我的导数比你的大。导数是什么意思?宝宝们,导数是变换的速率,就我变,我在增,你也在增,但是我增的比你快哟,我增的比你快哟, 啥意思啊?就是你这个孩子头像在我的底下哎,所以我画这个图像,我把他俩放到一块去吧,宝宝们,就是 tatax 增的比这个 y 等于 x 要快,也就是,哎,是这样的哎,在零到二分之派的时候哈,宝宝们零到二分之派的时候是这样的啊,那,那左边固然也就是这样的了,宝宝们,是吧?所以探听 x 比外地面 x 是大的,是大的啊,他俩的交点只有一个,就是在这个零零的时候,零零的时候,懂了吗?一键三零幺,拜拜,爱你们。
 00:27
00:27
猜你喜欢
最新视频
- 1272粽小Q









