高二数学轨迹方程解题方法
粉丝7.6万获赞42.6万
相关视频
 15:21
15:21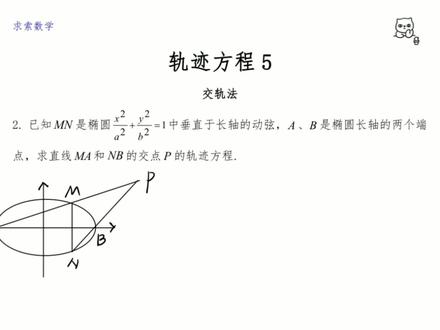 03:42查看AI文稿AI文稿
03:42查看AI文稿AI文稿大家好,这个视频我们要讲的是轨迹方程的第五种求解办法,交轨法,也就是焦点的轨迹方程,最常见的题目呢就是两个直线的交点的轨迹,那么两个直线的交点如果是一个轨迹的话,意味着两个直线都在移动,那么也就是说直线的方程里边必须含有参数才行。 所以我们的第一步操作就是寻找这样一个参数,然后把两个之间的方程给他写出来,最后我们再削掉参数,就能够得到他们焦点的轨迹方程。我们来看下这个题目,这里告诉我们 mn 是垂直于椭圆长轴的一个动线,我们给他换了一个图像, ab 是左右的端点, ma 和 nb 的焦点为 p, 我们这里给他画了一个图,然后让我们去求这个 p 点的轨迹方程。这里的话,首先我们就应该把我们已知的一些点的坐标给他写一下,对吧? ab 两个点的坐标我们是知道的, a 点的坐标呢,是负 a 零, b 一点的坐标是 a 零,然后的话 mn 两个点它是上下对称的,所以如果我们要设坐标的话,其实只需要一组就 ok 了,对吧?我们来设一下, 设 m 点的坐标是 x 零和外零,则 n 点的坐标我们就知道了,对吧?他就是 x 零和 副的外领,这里看似是两个参数啊,实际上是一个参数,对吧?因为 x 零和外领还满足一个关系是,就是 x 零的平方比上 a 方,加上外零的平方比上 b 方,他等于一,因为这个点在我们的椭圆上,对吧? 所以实质上只有一个参数,那么这个式子呢?是我们等一会用来替换的一个式子,好了,下来我们来写直线的方程,我们先来写 ma 的直线方程,这里的话,我们可以用 ma 两个点的坐标 把他的斜率表出来,对吧?也就是 y 零比上 x 零,再加上 a, 然后写一个点些是 y 等于斜率,再乘以 x, 再加上 a。 同样的道理, nb 这套直线我们也可以这样来写,也就是 y 等于负的外零,比上 x 零,再减去 a, 然后后边乘上 x 减去 a。 我们发现啊,我们一开始写的这个式子呢,里面是平方的关系,对吧?所以这里的话,我们要想办法去构建平方。构建平方的话比较简单,我们观察发现他们很多地方沉完以后都是平方差,对吧?所以我们考虑把这两个式子沉一下,我们给他命名, 这是一式,这是二式,我们用一式乘以二式就可以得到 y 的平方,他会等于负的 y 零的平方,再比上 x 零的平方,减去 a 的平方,后边再乘上 x 科四的平方,再减去 a 的平方,对吧?好了,那么我们来替换一下,替换一下的话,我们就可以用刚才写的这个式子,把外零的平方给他算出来,对吧?这里的话,外零的平方他就会等于 b 方,再减去 a 方,分之 b 方,再乘以 x 零的平方,对吧?我们同时提一个 a 方分之 b 方,那么这里就是 a 方,再减去 x 零的平方,好了,我们把它替换一下。替换以后呢,他就可以写成 y 的平方,会等于 这里是 a 方,分之 b 方,然后上边的话,把两个位置倒一下,就是 x 零的平方减去 a 方,下边也是 x 零的平方减去 a 方, 然后再乘以 x 的平方减去 a 方,对吧?好了,那这里很明显啊,他们俩可以约掉,约掉以后我们把它整理一下,也就是 x 的平方比上 a 方,在减去 y 的平方比上 b 方,他等于一,对吧?我们得到了一个双曲线,但是这里需要注意一下啊, 他不是一个完整的双曲线,因为什么呢?因为 p 不可能在 ab 两个点,对吧?那这里的话我们就要规定一下,你可以写 x 不能等于正负 a, 或者是 y 不能等于零,对吧?这就是他完整的轨迹方程。
1196求索数学 04:37
04:37














