函数零点存在定理
粉丝1.2万获赞6.4万
相关视频
 00:18查看AI文稿AI文稿
00:18查看AI文稿AI文稿恋爱脑带你学高数之零点,存在定力函数在 x 轴两端的点,连续这两点间一定与 x 轴相交,存在零点。我的意思是,哪怕你和他站在了对立面,只要心还连在一起,你们之间就还有机会听懂了吗?
3643今夜不挂科 01:27
01:27 13:33查看AI文稿AI文稿
13:33查看AI文稿AI文稿杰哥,十分钟讲清楚倒数零点定理和倒数介值定理。哈喽,大家好,数学是思维体操,我是考研数学杰哥,关注杰哥学习更多的考研数学技巧。今天呢,我们这节课主要给大家讲倒数零点定理与倒数介值定理。 那说起来,零点定理和戒指定理大家实际上都比较熟悉了,那为什么要在这两个定理之前呢?加上导数两字, 实际上我们零点定理或者近日定理是针对某个函数 f 来讲的,对不对?那么我们这里面这个导数,实际上呢, 它应该是导函数的意思啊,所以我们全称导函数,零点零零导函数。接着 经理,那么在说这个之前呢,我们先来回顾一下咱们零点定理。戒指经理啊,他们俩都有个前提条件,就是咱们这个 f, 咱们这个函数啊, 得在 b 区间 a 到 b 上连续才能够使用,比如零点零零啊,得是连续还是在 b 区间上? 两段函数是一号,那么在在这个开卷内肯定存在某个零点啊,这个很简单,戒指定理也是啊,我们 b 圈上连续函数如果有一个实数呢,是他介于咱们这个,呃,小 m 到大 m 之间 啊,那这个情况下一定存在某一点,这个函数值呢,和这个 miu 相等啊啊,咱们这个小 m 大 m 呢,实际上是连续函数在 bgm 上的一个最小值到最大。 好,那我们现在导函数的介质定理与导函数的零点定理,它关键不同就在于这个函数不一样,你看咱们这个函数 f, 咱们这个函数 f 是随便哪个函数都行啊,但是我们导函数呢,是一个 f 撇啊,它是某一个 函数的导数啊,那么它就和咱们一般的零点定理和介指定理呢,就有不同了啊,它就有不同点了,那不同点到底在哪里呢?我们一起来把这一道题目做了就知道了, f x 在 a 到 b 上可倒, 首先一个呢,我们先把这个条件给解读一下, f x 在 a 到 b 上可倒,那是不是就说明 f x 在咱们 a 到 b 上肯定也是连续的,对不对?但是由于我们导函数呢,也是可以有间断点的啊,所以他没有说连续可导的话,就说明 f、 e、 p、 x 在咱们 b 区间 a 到 b 上啊,可以有间断点, 对不对?好,那这个条件呢,已经挖掘完了啊,我们来证明,第一个导数,零点零零, 如果 f 倒 a 证乘 f 倒 b 负小于零,这句话告诉我们三层意思,第一层意思是 f 倒 a 证和 f 倒 b 负是存在的。 第二层意思是这两个数没有等于零的,因为它俩相乘小于零,你要等于 两个数中之间有一个数是零的话,那么成绩应该是零,对不对?第三层意思是这两个数字呢,一正一负。那在我们证明体证明的过程中呢,常常有个不防证啊,因为 它俩相乘小于零,就会有两种情况, f 导 a 证是正或者 f 导 a 证是负啊。不过呢,我们证明方法都是一样的啊,所以我们只需要宅某一种情况去证明啊,另外一种情况咱就同理啊。 所以这时候呢,我不妨设 f 倒 a 正是大于零的, f 倒 b 负呢,是小于零的, 那么我们可以按照定义呢,把 f 倒 a 证 写出来 对不对?好,这时候根据咱们函数极限的局部饱耗性,咱们可以知道,一定存在一个 delta 一大于零,当 x 属于 a 到 a 加 delta 一时, 我们有 f x 减 f, a 比上 x 减 a 肯定大于零,对吧?哎,我们把这个 limit 符号去掉,之后的这个函数呢,在某个领域内,它的符号保到咱们极限的符号, 由于分母呢是大于零的,所以分子也大于零啊,所以我们由这个可以知道, f x 实际上比 f 一要大。 好,接着呢,我们 f 倒闭付,我也按照定义 去写一下, 各位来看,一定存在一个 delta 二大于零,当 x 属于 b 减 delta 二到 b 时, 我们有 f x 减 f, b 比上一个 x 减 b 小于零,还是根据在函数极限的局部饱耗性,这时候呢,分母是负的啊 啊,所以我分子肯定是是正的啊,正的除负的才能是小于零,对不对?好,那说明还是 f x 要比 f b 要大, 所以我在开区间 a 到 b 内总有某一点处的函数值, f 呢,比 两端点的函数值要大,所以 f a 或者 f b 都不可能取得最大值。由于 f x 在 a 到 b 上连续 f x 的最大值 在开局键 a 到 b 内取得, 那我们就设 f x i 是等于 max x 大于等于 a 小于等于 b f x。 啊,我们 f 在 p 区间 a 到 b 上的最大值呢,给它设成了是 f 和三。 好,各位,我们可导函数不在区间端点处取得的最大值一定是极大值,该点处的导数呢,根据飞马盈利一定是零。 好,所以 f 一导克赛等于零整理完毕。好,我们反过来看一下,大前提是 f p x 实际上大前提是 f p x 在 b 区间 a 到 b 上存在, 这是咱大简体啊,这个函数啊,在 b a 到 b 上处处处处有定义啊,处处存在,不一定连续。但是呢,咱们 f e p x 却具有零点定理的性质啊,只要两端点处 f e p x 在两端点处的取值 呢?一号,那我在这个开间内一定某一点处啊,这个 f e p x 是零。好,这个就是我们导数零点零零跟普通零点零零不一样的地方。 好,接着呢,我们倒数零零零里,实际上是为我们后面倒数戒指定理证明呢做铺垫的啊。接下来呢,我们一起来正第二个,我们正倒数戒指定理, 前提条件是这俩不相等,这俩不相等呢,实际上就告诉我们另外一层含义,就是 f 岛 a 证和 f 岛 b 负都是存在的啊,它都存在。 现在呢,有一个实数 mil, 它介于这俩数之间, 注意,他介于这俩数之间呢,这种情况下,咱们这个 miu 呢,他不能和他两个数中的任一个数相等。哎,就说 miu 肯定是。呃,要么是大于 小于这种情形啊,要么是大于小于这种情形啊,这是两者取其一啊,不能带等号,这个是我们导出界的定理。这边这个介语的意思啊, 好,那既然呢,我们这个实数 meal, 它介于这之间还是一样,我们就来个不防,正 因为我们这个 meal 跟 f 倒 a 证和 f 倒 b 负的大小关系,对于我们去证明的这个方法呢,没有任何影响,所以我们依然不防设 在这个 mill 呢,是大于 f 岛 a 正,小于 f 岛必负的。好,各位来看,让我们去正的这个东西啊, 你把它改写一下,是不是 f 一到可赛减去 mill 等于零啊?这个东西呢,我再改写一下,它是不是一个 f 一到 x 减去一个 mill 在 x 等于可赛处的取值啊? 那你看这个东西是不是某个函数的导数,比如说 f x 减去一个 mill, x 的导数在 x 等于可赛处取之是零啊,这是说明导函数的导函数存在零点,那可不就用咱们导 小数零点定理吗?哎,所以这个时候呢,我们不妨就设一个大 f x 等于 f x 减去 mill x, 那大 f 一到 x 呢?就 f 一到 x 减去咱的 mill。 现在我只需要去找大 f 一到 x 在区间端点处一号就证完了。 那 f 倒 a 证,我们用定义可以直接得到 f 倒 a 证减 mill, f 倒 b 负, 我们用定义也可以直接得到 f 到 b 负减。缪,那有同学说,哎,杰哥,你这边能不能不要省,你给我写一下啊?行,可以,他呢,按照咱的定义,这就是 x 区域 a 正大 f x 减大 f, a 比上 x 减 a。 好,这时候我们分子写上去啊, f x 减去 miu, x 减去 f a 减去 miu, a 比上 x 减 a 啊,那分子呢,实际上就比如写成 f x 减 f a 括号减去 miu, x 减去 b u a 除以咱们的 x 减 a。 好,这里面这个 miu 呢,我提出来 啊, miu 呢?提出来好,这时候你看这部分极限存在就是 f 导 a 证,这部分极限存在就是副 miu, 是不是啊?啊,所以呢,我们这块就不详细说了啊,后边这个实际上是同理的,那现在同志们, 我们的 meal 是不是满足这个不等式?那么我们大 f 岛 a 证乘大 f 岛 b 负肯定是小于零的 啊,肯定小于零,因为,因为这个 mill 呢,比我们 f 岛 a 证要大啊,所以这是小于零的 mill 呢,比咱 f 岛 b 负要小,所以这是大于零,它的相乘当然是一号了。好,那么由咱们导数零点定理 可知,好,一定存在某一点可塞属于咱的 a 到 b, 使得大 f 一到可塞等于咱的零,那也就是 f 一到可塞等于咱的 mu, 对吧?好,还是反观一下, f e、 p、 x 在 a 到 b 上不一定连续,但是呢,我依然能够发现我们导函数呢,在 b 选 a 到 b 上具有 戒指定理的形式。好,那这个就是两个定理给大家介绍的啊,希望大家呢,能够把这个两个定理呢能够 学会啊,我们正品的过程中呢,又用到了我们不防正这样一个技巧,大家以后自己在做正品题的过程中呢, 应该会经常用到的啊,你多用多训练,你就慢慢就变成你的了。然后呢,我们也用到了咱们含日金的局部保号性,对不对?所以融会了很多咱们呃最基础的一些知识,希望大家能够在这节课里面学到很多知识啊。啊,那大家也可以把自己的过程呢 打卡在评论区啊,我们可以在评论区交流,杰哥会看到,如果大家觉得视频讲的不错的话,一定要给杰哥一个三连,多多支持杰哥的创作,那我们下期节目再见了,拜拜。
878考研数学杰哥(线下)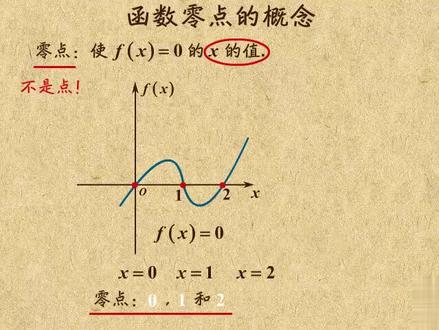 01:36查看AI文稿AI文稿
01:36查看AI文稿AI文稿这个视频我给你讲讲函数的零点。一般的函数的零点是指使得函数 fx 等于零的 x 值。 注意,零点可不是一个点,他是一个数值。比如函数 fx 等于二, x 减六, x 等于三十,函数值为零,那这个函数的零点就是三。注意,在这里,你只能说零点是三,绝对不能说是 x 等于三,更不能说是三零点。 同样的,如果是这个二次函数 x 等于一和三十,函数值都等于零,那这个函数就有俩,零点、一和三。注意,在这里 你只能说零点是一和三,绝对不能说是 x 等于一和 x 等于三,更不能说是一零点和三。零点以上就是零点的概念。从前面的过程可以看出,函数 数 fx 零点跟方程 fx 等于零的根,以及函数 fx 与 x 轴的焦点是一一对应的。比如已知定义在而上的函数 fx 图像与坐标轴的所有焦点为零,零一零和二,零, 那方称 fx 等于零的根就有三, x 等于零, x 等于一和 x 等于二,而函数 fx 零点也有三,零一和二。好了,就讲这么多, 总结一下吧。这个视频我就给你讲了什么是零点,注意,零点不是点,而是一个数值。函数 fx 有几个零点,就说明方程 fx 等于零,就有几个不同的根,而函数图像就跟 x 轴有几个焦点。怎么样,明白了吗?明白了就赶紧刷题去吧!
1810若愚 14:56查看AI文稿AI文稿
14:56查看AI文稿AI文稿这节课我们一起来学习函数零点存在题里,现在看一下这条题里,如果函数 y 等于 fx, 在必须 ab 上的图像是一条连续不断的曲线,且有 f a 乘上 fb 小于零, 还是 y 等于 fx 在开区间 ab 内至少有一个零点,即存在 c 属于开区间 ab, 使得 fc 等于零,这个 c 呢,也是方程 fx 等于零的解,这句话怎么理解?我们来用一句更简单的话来描述一下, 函数 y 等于 fx 在 b 区间 ab 上满足两个条件,第一个条件,他的头像是连续不断的。第二个条件, f a 乘上 fb 小于零,两个端点的函数值相乘以后小于零,说明 f a 和 fb 他们俩是一号的,然后 f a 大于零, fb 就小于零。 当 f a 小于零, a b 就大于零,才能满足生成以后小于零。当一二两个条件都满足的时候,我们得出这样的一条结论, y 等于 fx 在开始键 a b 上至少有一个零点, 至少有一个零点,说明可能有多个零点的情况,但是满足最少有一个零点。好,画图来帮助理解一下, 这是 a 点,这是 b 点。当 f a 大于零的时候, fb 必定小于零。他们的图像是连续不断的,要把他们俩连起来,那么必定会经过 s 轴,所以必定会有一个零点。当, 当然也会有多个零点的情况。我们来画一下,这是 a 点,这是 b 点。假设 f a 小于零, fb 呢?必定大于零。好,我们穿过 s 轴 多次,那就会有多个零点,比如说这种情况,这里有一二三四五六七,这里有七个零点,这是有关零点存在定理。 我们在这个地理上做一点点的变更,把这个图像连续改成图像不连续,看看他是否有零点 好。同样我们选择 ab 两个点, f a 大于零, fb 呢?小于零。当他们图像不连续的时候,比如说在这里他突然断开了,好看一下这个时候有没有零点, 是不是也是有零点的?这是第一种情况。好,我们再看一下,这是 a 点,这是 b 点, f a 大于零, fb 呢小于零,这个时候呢,我们在这里也断开了,但是呢, b 点 这边连的时候是在下边的,这个时候是不是没有零点?就是第二种情况,会不会也有多个零点的情况呢?我们来画一下。当然也有多个零点的情况,多穿 s 轴几次,他就会有多个零点, 这里穿了以后在这里断了,这里呢,我们也是穿了以后中间会有个断点,那么这里也会有多个零点的情况,这是图像不连续的时候,会有几种情况,一个零点没有零点,多个零点都是可以的。 第二种情况,我们把 f a 乘上 fb 小于零,改成 f a 乘上 fb 大于零,会不会也有零点或者没有零点呢?我们来看一下,这样 f a 乘上 f b 大于零,说明他们俩同号,要么两个都大于零,要么两个都小于零。假设 f a 和 f b 他们俩都大于零, 在这里的情况,如果直接这么连,是不是就没有零点好,来看一下,当他们俩都小于零, f a 和 fb 都小于零,这种情况,我们来看一下 他会有几个零点,一二三四五六,他会有六个零点,当然有没有只有基数个零点的情况呢?我们来画一下。 f a 在这里, fb 在这里,一定要保证他们俩同号才能满足 f a 乘上 fb 答应你。这里当相切的时候是不是只有一个零点,他就是基数零点,我们还可以画一下,也是基数零点的情况,这里相切一个,但是另外都是穿过去,我们看一下是不是基数零点,一二三 四五六七,他是有七个零点,所以他既可能没有零点,也有可能有计数个零点,也有可能有偶数个零点,这是当 f a 乘差 b 大于零的时候。好,接下来我们把 f a 乘上 mb 小于零,来看一下是否有唯一零点。 其实上面有讲了,当这种情况下的时候,他只有一个零点,当这种情况呢?他这里有七个零点,所以不一定有为零点,但什么情况下是有为零点呢?当 零点存在加上函数单调的时候,他是有为零点。比如说这种情况,他函数单调递减,所以只会穿 x 轴一次,不会穿多次,他穿过来了就不会回去了,这是只有一个零点情况,加上函度加上函数单调,那么就只有一个零点。 接下来看一下第四种情况, f a 乘上 a b 小于零,零点个数是否为计数个?我们来看一下这种情况,他是计数个,这种情况他也是计数个, 那么会不会有偶说过的情况呢?我们也画图来看一下, f a 在这里, fb 在这里,我们当有一个点相切, 然后再穿的时候,我们来看一下是有几个零点,一个、两个、三个、四个、五个、六个、六个零点。记忆可能有技术个零点,也有可能有偶数个零点,所以这句话是错误的。 好,这是有关零点存在定理,我们要注意的几点,第一,他的图像是连续的,第二呢, f a、 f b 他们俩相乘以后是小于零,端点函数值相乘小于零,那么在这个区间上至少有一个零点, 也有可能有多个零点,情况可能是基数个零点,有可能是偶数个零点。当这个函数零点存在,且函数是单调的时候,那么零点就是唯一的。 接下来我们做一下练习题,来巩固一下判断零点所在区间。第一题,函数 fx 等于落音, x 减去 x 分之二,他的零点所在的大致区间是在哪里? 像这种判断零点所在区间,通常情况下他会给出一个函数解析式,然后在选项里边会给出几个区间。 我们解题的方式是把区间端点的值带进函数解析式,看一下他的函数值的正负。如果端点函数值是一号的,那么在这个区间必定会有零点。用这个方法我们来做一下。第一个,我们先把 f 一带进去, 把这个端点的值一带进来。 f 一是等于任意一减去二比上一是等于二,那一是等于零,零减去二是等于负二,他是小于零。 接下来我们把二带进来, f 二呢是等于录音二减去二,比是二减去一,录音二他是小于一,一小于一减去一的话,那么也是小于零。 f 一和 f 二都是小于零,所以中间不一定保证会有零点。好,我们看一下,把三带进来, f 三呢是等于烙印三减去二, 二比上三,任意三是大于一,二比上三呢是小于一,那么相减以后就大于零,这个 f 二他是小于零,我们已经算出来了, f 三呢是大于零, 这里小于零,这里大于零,说明中间必定会有一个零点,所以答案会选 b 选项,我们看一下 d 选项里边有一个 e, 我们把 e 也带进来看一下。 fe 是等于任意 e 减去 二比上一,那一是等于多少?等于一,一减去二比上一,他是一个小于一,因为一等于二点七一八二八相除以后,小于一的话,相减以后是不是就大于零? f e 大于零, f 三大于零,但是 e 是比三小的,所以我们能把 b 选项他明天所在区间的范围缩的更小,是变成二到一这个开区间。 现在如果我再问你嘴在二到一这个开区间有几个零点?第一种情况,我们根据之前所学的零点个数的判断,我们令 fx 等于零,也就是 fx 等于诺 ex 减去二比上 x 等于零,我们来看一下诺 ex 等于二比上 x, 假设 hx 是等于诺 ex, x 呢,是等于二比上 x, 画出他们俩的函数图像,当这两个函数图像有几个焦点,就有几个零点,画一下他们函数图像,大概是 这个样子。二笔上 x 是反比点函数,在第一项线是单调减的,从图中我们可以看出,他们有一个焦点,在零到正无穷,有一个焦点,这个区间缩的更小,就是二到一这个开区间, 所以他只有一个焦点。我们利用函数零点个数的判断来做画图,求焦点个数,然后直到零点个数。 当然我们也有第二种方法,就是今天我们所学的根据函数单调加上零点存在,这样有零点,那么根据函数单调来看一下,我们看一下这个函数是单调还是不单调。任意 x 是大 单调,真的二比上 x 啊,他是一个反比例函数,在第一项线是单调减的,一个单调真的函数减去一个单调减的函数,他是单调增还是单调减呢?我们来写一下单调增,减去单调减, 是单调增还是单调减?回忆一下之前所学的增函数加增函数是增函数,减函数加减函数是减函数,而增函数减去一个减函数,它是一个增函数,所以它这里是一个增函数。最后我们来看一下减函数减去增函数,它是一个减函数, 是我们之前所学的符合函数的增减性问题。同加不变易减,同前同加的话,不变而易减呢?同前面这个就行了。当然我们也可以理解为增函数是一个正数,正数加正数是正数,而减函数呢,是一个负数,负数加负数是负 负数,正数减负数是正数,负数减正数是负数,正,理解也可以。好,我们回到这个题,这样说,这是一个真函数,这是一个减函数,相减以后是一个真函数,那么 fx 他就是一个单调真函数。 零点在这个里区间里边存在,而他就是一个单调真函数,那么我们可以确定他的零点是唯一的,在这个区间里边有唯一的零点,这是有关。第一题,用两种方式我们可以判断在这个区间有唯一零点。 第二题,函数 fx 等于一的 x 方,加上 x 减去二,他的零点所在的一个区间大概是在什么样的位置?同样,我们把这个区间的端点值都带进去,看一下他们端点函数值是否一号。先来带一下 f 负二负二带进来,一的负二次方是一的平方,分之一,再减去二,减去二,这里是小于一的,减去四的话是小于零。 f 负一再带进来以后呢,我们看一下,是一分之一减去一,减去二,小于一减去三,他是小于零,这里 f 二小于零, f 负一小于零。 咱们端点函数值是同号的,不能保证在这个区间有零点,所以 a 选项排除,看一下 b 选项,我们把零带进来。 f 零是等于 一的零次方式等于一,一减去零,再减去二,就一减去二是等于负,一是小于零。好,这里函数值小于零,这里函数值也小于零,所以不能保证他们区间里边有零点。看一下,我们把一带进来。 f 一是等于一,加上一减去二, 二是等于一,减去一,一是二点七八二八减去一是大于零的 f, 零是小于零。 f 一呢,是大于零,这里小于零,这里大于零。端点函数指一号,所以在 c 这个选项里边,他具有零点,答案就选 c 选项,这是有关判断零点所在区间的问题。 好,同样我们来看一下这个函数在这个区间里边有几个零点。我们利用函数单调性来看一下,一的 x 次方在这个区间是单调真的,而这里呢,一次函数 x 减去二,他也是单调真的函数,单调真的函数加上一个单调真的函数,他依旧是一个单调真的函数。 f x 在零到一这个区间里边单吊针,那么零点存在,加上他是单吊针,必定只有一个零点,这是有关这个 第二题,接下来我们继续做一下判断零点所在区间的练习题,这个题在上面基础上稍微做了一点点的变更。若 x 零是方程二分之一的一个次方等于 x 三分之一次方的解,再问 x 零属于哪个区间, 这个题该怎么做?先问的是方程,而之前我们所说的是函数零点的问题,我们把这个方程转换为函数 数来看一下。我们令 fx 等于二分之一的 x 方,减去 x 的三分之一次方,那么他是 x, 零是他的解,我们可以转换为 x, 零是这个函数的零点来求解来看一下。 好,既然求他的零点所在区间,我们只要把这区间的端点值带进去,然后看他们端点函数值是否一号,如果一 一号是有零点,那么如果不一号,就不能保证有零点。先来带一下最小的,我们把零带进来看一下。 f 零 等于二分之一的零次方是等于一零的二分之一次方式等于零,所以一大于零,好,再带一下三分之一。 f 三分之一是等于二分 之一的三分之一次方,减去三分之一的三分之一次方,这个时候呢,底数不同,但是指数相同,怎么样来比较大小? 我们有讲过指数相同,底数不同。那么利用密函数单调性进行比较,密函数单调性,回忆一下 y 等于 x 的阿尔法脂肪,当阿尔法大于零的时候单调增,阿尔法 小于零的时候单调减,这里阿尔法是等于三分之一。三分之一大于零,那么函数是单调增的,比数越大,函数值也越大二分之一, 所以二分之一的三分之一次方减去三分之一的三分之一次方是大于零的。接下来 我们把二分之一带进来。 f 二分之一是等于二分之一的二分之一次方减去二分之一的三分之一次方。他们俩怎么比较大一下呢?底数相同,指数不同,我们利用函指数、函数单调性进行比较,指数、函数单调性也回一下。 y 等于 a 的 x 方,当零小于 a 小于一的时候,函数单调减, a 大于一的时候呢?函数单调增,这个时候呢? a 是等于二分之一,他是小于一,那么函数单调减,指数越大,函数值反而越小。二分之一比三分之一大,所以他函数值反而越小,就是小于零。
138滴答课堂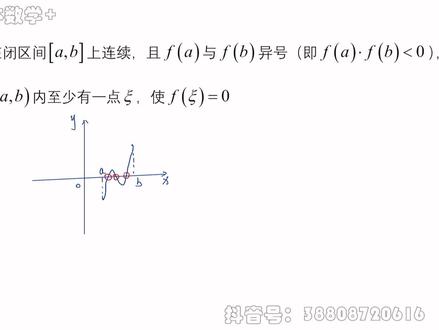 02:33查看AI文稿AI文稿
02:33查看AI文稿AI文稿我们可以总结一下,零点定理需要满足两个条件,一是函数 f x 在 b 区间 a 到 b 上连续。二是函数 f x 在端点值一号,以及是他们的端点值乘起来小于零。 满足这两个条件就可以得到一个结论,至少存在一点可赛,属于 a 到 b 的开区间,使得 f 可赛等于零。我们来学习一下零点定理。零点定理是这样的,设函数 f x 在 b 区间 a 到 b 上连续 写 f a 与 f b 一号,其 f a 乘以 f b 小于零,那么在开区间 a b 内至少有一点可晒,使得 f 可晒等于零。这个定义给到大家后,可能大家也不知道他说了个啥,或者说有一点明白,但是没有什么具体的感受,我们可以用图像 来更清晰的认识他。首先在我们的定义中,他的两个端点值是一号的,也就表示这两个端点一个在 x 轴的下方,一个在 x 轴的上方,而这个函数在这两点间又是连续的,也即是这两个点 可以用一条完整的线连接起来,那不管这条线是一条曲线还是一条直线或是别的什么线,只要你要将这两点连接起来,而且一个在 xo 下方, 一个在 x 轴上方,那么就一定会经过 x 轴,至少经过一次,而与 x 轴的交点就是我们所说的零点,这就是零点定理。 两个条件推出了一个结论,我们可以总结一下,零点定理需要满足两个条件,一是函数 f x 在 b 区间 a 到 b 上连续。二是函数 f x 在端点 点值一号,以及是他们的端点值乘起来小于零。满足这两个条件就可以得到一个结论,至少存在一点可赛属于 a 到 b 的开区间,使得 f 可赛等于零。 理解了零点定理之后,我们就可以知道,其实零点定理中证明的零点本质就是在寻找 f x 等于零的根的存在性。我们去做这类题目的时候,就只需要抓住它的关键点,也就是 f x, 而我们的 f x 一般在题目所需要证明的结论中,有时需要将我们的结论一项, 得到我们的 f x, 找到 f x 之后再去验证他是否满足这两个条件,满足条件之后就可以使用零点定理证明结论,这就是我们解题的思路。以上就是零点定理,请持续关注,接下来会给大家讲解二零一五年的第二十一题。
42升本数学+
猜你喜欢
最新视频
- 2059艳姐手工











