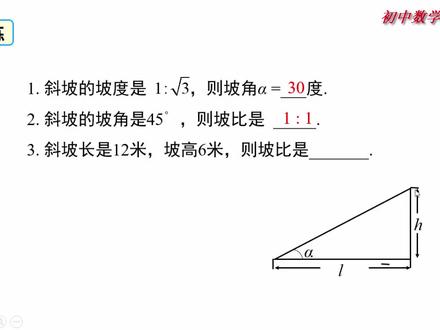
坡度和坡角的定义
粉丝20获赞100
相关视频
 16:38查看AI文稿AI文稿
16:38查看AI文稿AI文稿各位朋友们大家好,这节课我们来学习用坡度来解,这叫三角形。首先我说明的是在人教版教材中没有出现坡度和破笔的概念,只在课本的第七十七页出现了一个练习题。 这节课我打算讲讲解一下坡度和破笔的基本概念,以及它的简单应用。好,下面我们先来看坡度和破笔的概念。 首先我们观察思考一下,如图,从山脚到山顶有两条路, ab 和 bc, 问哪条路比较陡? 从图上大家可能直接看出 bc 这条路肯定是比较陡的,那么 bc 这条路比较陡该 该如何用一个数量来刻画?他就要懂了, 有哪些职能股?课程喊出来 很容易,大家想到的就是角度。对,这就是我们说的第一个问题,坡角。坡角可以表示一个坡面的倾斜程度, 那么坡角是什么呀?这样是一个坡面,然后呢还有一个水平面,这是一坡面和水平面组成了一个假角,我们就叫做坡角,通常用耳法来表示, 所以说坡角就指坡面与水平面的加角,那么这个数值可以刻画一个坡面的陡 跳程度,那么除了这个孩子有一个能够计算表达他们的陡峭程度,那么这份啊,坡度或者叫坡比。 什么是坡度和坡比呢?我们从坡面的顶端向水平面做一道垂线,那么这个垂线的长度其实就是这个坡面的铅垂高度, 那是在水平面上脚的顶端顶点和刚才做的垂线的垂足之间, 水平面的长度是这个鞋面的水平距离,那么水平 数值高度与水平长度的比值就是我们说的坡度或者破比,所以说坡度破比的概念就是坡面的千锤高度和水平长度的比值,叫做坡面的坡度和破比。 通常我们用爱来表示,爱等于他的铅垂高度与水平距离 l 的比值。这是啊,在我们一些工程图纸上的通常标志方法。用坡度来表示 坡度,通常可以写为一比 m 的形式,比如说一比六啊,一比二,一比三等等。从 这个图上我们可看出来,坡角和坡度有一定的关系。把这个坡面做了前垂高度之后,可以发现构成一个直角三角形,那么坡角阿法对边就是我们前垂高度, 棱边就是水平长度,所以说这个坡度其实就是这个坡角的对边和棱面的比值,那么 r 就等于 h b l 其实就等于餐厅的 r, 那么也就是说坡度和坡比 等于坡角的正切值。好了,了解一下坡度的概念之后,先来看一个小练习, 如图,坡度的啊,斜坡的坡 度等于一比零三,问坡角儿法多少度?大家们可以看出来, 斜坡的坡度是一笔开三,即竖直高度与水平距离的笔直是一笔开三, 相当于在这个直角三一中叫 f 的对边与零边的比值及他的正斜值等一比零三,也就是三分零零三,可以知道这个角度应该是三十度。 第二,如果斜坡的坡角耳法是四十五度,用坡比,如果斜坡的坡角是四十五度,我们做了牵垂高度与水平距离构成直角三角形的话,那么这就变成一个等腰直角三角形,那么他的竖直高度与水平距离的比值就是一比一。 第三,斜坡的长是十二米,坡高是六米,问坡比是多少? 那么斜坡的长度十二米,斜坡的高度六米,对于这个角坡角 f 来讲,其实就是他的对边,以斜边的笔直 啊,这边和斜边一个是十二,一个是六,显然斜边是他对边的二倍,那个阿尔法就等于三十度, 那么这样呢,就可以知道餐厅的三十度等于一比零三或者三分之三。但是这题还可以这样看,知道斜坡的长度十二米,斜坡高十六米,用 勾股定理可计算出写出的水平距离等于六比零三,所以坡比就等于六比六比零三,记一比零三好了,看完这几个练巧练习题,我们下面再来看两个人例题。 例一,如图,以山坡的坡度为二,等于一比二小。刚从山脚 a 点出发,沿着山坡向上走了二百四十米,到达点 c, 问这座山坡的坡角是多少度小,刚上升了多少米? 首先我们把这个实际的问题图形转化成一个我们常见的平面结合图形, 这样呢,就构成这样一个直角三形 abc, 他的坡比坡度是一比二,记 bc 比上 ab 是一比二,也就说这个叫 a 的正确值是一比二。 要求这个角的度数就可以用三角函数来给你计算。 像这样,我们用阿法表示坡角大小,那么根据题意可知道残留的阿法等于二分之一,我们用计算器可以计算出角度的大小。阿法约等于二十六点五七度, 下面要求他上升了多少,其实就是我们要求 bc, 这里面知道阿法等于二十六点五七度,我们用三角函数可以进行计算,因为要求的是啊 bc, 已知的是啊 ac 的长度是二百四,所以用他的对边与斜边有 cer 对 cer 法等于 ac, 从而求出 bc 的长度一百零七点三米, 这样呢,就知道他上升了这个一百零七点三米。不过这里面要说明的是,这一题中我们求第四长度的时候,用三角函数 有借助了这个二十六点五七度,这个呢是一个近似值, 在通常我们计算过程呢,尽量不采用中间的近四值进一算,那么我们如果不采用角,不用角 a 的度数也可以计算这个 长度。我们看这样,如果是 bc 等于 x, 那么因为这个斜坡二等于一比二,以 bc 变成 ab 等于一比二,所以可知道 ab 是二 x。 在这个直角三角形中,我们知道两直角边的平方和对啊等于斜边平方,即 x 平方加二十平方等于二百四十的平方,从而可以求出 x 等于一百零七点三。 这样呢,我们就不用中间的这个叫 a 的近似值,因为采用近似值的时候再参与运算,可能会产生比较大的误差。 好了,我们接着看立二立二水壶大坝的横斜面是梯形,坝顶宽六米,坝高二十三米, 斜坡 ab 的坡度二等于一比三,斜坡 cd 的坡度二等于一比二点五。第一步让我们求斜坡 cd 的坡角, 这里面我们 c 级的坡角已经告诉你他的坡度是一比二点五,也就是告诉了这个角的正切值,所以我们直接才知道斜坡的 坡度二等于弹琴二法等于一比二点五,就等于零点四。我们用计算器就可以算出来二法的度数是约等于二十二度。 看第二个问题,笔直坝底 ab 和斜坡啊,求入 ab, ab 和斜坡 ab 的长度。这里面我们先要从 bc 两点向 把底做垂线做 b, e 垂直 a, d, e 点, cf 垂直 a, d、 f 点。 根据体育我们可以知道 b 和 c、 f, 其实这就是这个大巴的高度,也就等于六米 啊,二十三米。还有就是 dc 和 ef 他们俩 啊,这样呢,构成一个矩形的对边,所以 bc 和 e、 f 都等于六。好了,这样呢,他两边就构成两个直角三角形。 在直角三星 abe 中,我们知道二等于一比三,这就是 be a, b 等于一比三,那这些可算出 a、 e 的长度等于六十九米。那么在职业三线 a、 b、 e 中,根据勾股定理,可计算 a、 b 的长度为这个斜坡 a、 b 的长度就可以算出来约是七十二点七米。 那么从在这个直角三行 dc, f 中,同理根据 c 这个坡比二等于 cfb, fd 等于一比二点五,就等于零点四啊,可以计算出 df 的长度等于五十七点五米。 那么这样再看 ad 的长度,就直接拿 ae 加上 ef 再加 df 就可以。再说他的总长度 是一百三十二点五米啊!这一题求出这题的答案,大的 ad 是一百二三十二点五米,斜坡 ab 的长度是七十二点七米。 好,两体立体。讲完之后,我们先来看一组练习 看。练习如图,小明周末上山踏青, 他从山脚处的必点出发侧的坡面 ab 的坡度为一比二,他走了二十倍的跟五米到达山顶 a 处, 这时他发现山的另一坡面 ac 的最低点的俯角是三十度,请求出 b 点与 c 点的水平距离, 在这里面没有直角三角形,显然构造直角三角形是我们必须要做的。从 a 点向 bc 做垂线, ae 垂直, bc 圆一点,这样呢,两边分别构成两个直角三角形。 在三型 abe 中,我们知道坡比坡度二等于一比二,你说 ae, 比如 be 是一比二,并且已经知道 ab 的长度是二十倍的跟五。 这些呢,我们有几种方法可以求出一个结果。你比如说我们用勾股定理是 a 零 x, b 零二 x, 然后勾股定理就给他算出 a b, 算上 a e 之后,那么 a e 和 b e 计算圈之后,我们再看在三角形 a、 c、 e 中, 下面知道从 a 点观测, c 顶的辅角是三十度,也就 d ac 等于三十度。其实还可以得出角 c 等于三十度,或者得 c, a, e 等于六十度。再知道 ae 等于 求出 a、 e 之后, c、 e 的长度自然也就可以求出来。这样呢,这个题就解决出来了,朋友们自己把这个解题过程写出来, 然后再看老师给出的参考答案。 看第二题。如图,河坝的横横断面是盈水坡, ab 的坡比是一比一,三把高比 c 等于三米,求坡面 ab 的长度。 这些呢,同学们自己解出答案就可以了,比较简单,老师就不再讲解 好。看下面一题,一段路基的横断面是梯形,高为四米,上底宽十二米 路基的坡,坡面与地面的坡比分别是一比一和一比分,三求路基下底的宽度。这时呢,我们刚才讲到第二, 比较近视, 大家看有没有思路。 当然,首先从 dc 两点向 ab 做垂线,这是必然要做的, 做两道垂线之后构成两个直角三线形, 再根据已知的坡度 再给你移植的坡度 和高等于四米。我们可以很容易修出 ae 和 bs 长度。比如说第一个由提议刻制做的两道垂线, 就是他的高度, be 和 cf 等于四米,而 cd 和 ef 和上底的高度都是十二米。 下面在三角形 ab 中,根据坡比等于一比一,而且 d 比 a 等于一比一,所以很容易求助 a e 的长度十四米。 那么在看只在直角三星 bcf 中很容易同理得出 bf 长度等于四倍的丁三米。 这样呢, ab 的长度就可以用三段的线段长加起来就可以了。再说这个路基下底的宽度约为二十二点九三米。好了,这节课就。
294初中数学学习1加1 07:45查看AI文稿AI文稿
07:45查看AI文稿AI文稿同学你好,这个视频我们一起来学习一下坡度。那么什么是坡度呢?我们一起来看一下。如图,从山脚到山顶有两条路,分别是 a、 b 与 b c。 问,哪条路比较陡呢? 很显然,从图中来看, c、 b 比较陡,而 a、 b 呢,比较平缓。那么问题来了,如何用数量来表示哪条路陡呢?我们来引入两个概念。第一个坡度, 坡度呢,也叫坡比,它表示的是坡面的垂直高度 h 与水平宽度的 l 之比, i 等于 h 比 l。 我们一般写成一比 m 的形式,比如 i 等于一比根号三。第二个概念,坡角,坡面与水平面的这个夹角 alpha 呢?记作坡角。在直角三角形中, alpha 的对边是 a、 h, 而阿尔法的零边是 l, 所以滩镇的阿尔法呢,就等于 h、 b、 l, 而我们知道 i 也等于 h、 b、 l, 所以知道坡度的时候,你就相当于知道了滩镇的阿尔法。 当坡度越大的时候,探证的 alpha 越大,此时坡角就越大,坡面就越陡了。那么如何用坡度解决实际问题呢?我们一起来看一道题,请同学先暂停视频,想一想再看答案吧! 好,这道题的答案是十二米,你做对了吗?咱们一起来看一下题。如图所示,某蓝水大坝的横截面为梯形 a、 b、 c、 d、 a、 e、 d、 f 为梯形的高。其中迎水坡 ab 的坡角阿尔法等于四十五度,这是四十五度 坡长 a、 b 等于六倍的根号二米, a、 b 呢,它是六倍的根号二米。被水坡 c、 d 的坡度 i 等于一比根号三。教你一招已知坡度,可以求滩镇的 c 坡度 i 呢,表示的是垂直高度 d、 f 与水平宽度 c、 f 的比,而我们的探证的角 c 呢,也等于对比邻,它也是 d f 比上 c f, 所以已知坡度的时候,相当于知道了探证的 c, 则背水坡 cd 的坡长是多少,我们一起来分析一下。首先要把这个实际问题转化成我们的数学模型,你观察一下,在这个图中有哪些数学图形呢? 左边的是直角三角形,中间的是矩形,右边呢,也是直角三角形。首先我们先来看一下直角三角形 a、 b、 e。 在直角三角形 a、 b、 e 中呢,已知一个角和一个边,所以它是可解的,那么 a、 e 就等于六倍的根号二,乘以三四十五度,就等于六米了。当然了,我们也可以用一个简单的方法来计算它,因为在等腰直角三角形中,三边比分别是 一比一,比根号二,我只需要用六倍的根号二除以根号二,就可以算出 a、 e 等于六米了。这个方法更简单。接着啊, a、 e 等于六米,那 d f 呢,也等于六米。 因为被水泼, c d 的坡度 i 等于比根号三,所以滩城的角 c 就等于一比根号三。我们化解一下啊,就可以得到三分之根号三。那问题来了,已知滩城的 c 等于三分之根号三,你能求出角 c 的度数吗? 没错,角 c 等于三十度,这个三角形呢,就是一个含三十度的直角三角形。那根据含三十度的直角三角形中,三边比是一比二,比根号三,我们就可以得到 d, c 呢,等于两倍的 d, f 就等于两倍的 a, e 就等于十二米了。 一起来摆你一道,请同学先暂停视频,想一想再看答案吧!好,这道题的答案是 五米,你做对了吗?教你一招, i 等于 h、 b、 l 等于碳真的 alpha, 知道坡度的时候,我们可以求出碳真的 alpha 的值。咱们一起来看一下题。某小区开展了行车安全方便居民的活动,对地下车库呢做出了改进,如图,这小区原来的地下车库的入口处有斜坡, a、 c、 a、 c 长呢十三米,他的坡度 i 等于一比二点四。知道坡度了之后呢,我们就相当于知道了 ab 比上 bc 的值, ab 比上 bc 就等于一比上二点四。化减之后等于十二分之五。 知道了滩镇的角 a、 c、 b 也知道了滩镇的角 a、 c、 b 呢,就等于十二分之五了。我们再来读题,为了居民行车安全,现将斜坡的坡角改为十三度,也就是角 a、 d、 c 这儿呢,它等于十三度,此时 b、 c、 d 在同一直线上。第一 一问,求这个车库的高度 a、 b 怎么求 a、 b 的长度呢?没错,解直角三角形 a、 c、 b 就可以了。那直角三角形 a、 c、 b 可解吗?已知一个角和一个边,所以啊,它是可解的。 我们知道滩镇的角 a、 c、 b 的值,也就是知道了 a、 b 与 b、 c 的比值,而题目中给我们的是斜边,所以我们可以设 a、 b 等于五 x, 则 b、 c 就等于十二 x 了。根据勾股定理,我们可以得到 a、 c 呢,它就等于十三 x 了, 而 a、 c 它是十三米,所以十三 x 等于十三米,那 x 就等于一了。那想求 a、 b 的长度呢? a、 b 是等于五 x 的,所以 a、 b 就等于五米,那么这个车库的高度 a、 b 就为五米了。接下来我们来看第二问,请同学先暂停视频,想一想再看答案吧。 好,这道题的答案是九点六米,你做对了吗?我们一起来看一下。求斜坡改进后的起点地与原起始点 c 的距离,那也就是说求 dc 的长度,结果精确到零点一米, 我们来看看啊。想求 d、 c 的长度,而 d、 c 呢,等于 b、 d 减去 b、 c, 咱们先来求一下 b、 d 的长度。怎么求 b、 d 呢?我们可以解直角三角形 a、 b、 d。 解这个直角三角形,你就能求出它的直角边的长度了。那这个直角三角形可解吗? 已知一个角和一个边,所以这个直角三角形呢,满足可解条件,那我的 b、 d 是能求出来的。再来看一下 b、 c、 b、 c 呢?在直角三角形 a、 b、 c 中,已知两边满足可解,可以用勾股定理求出 b、 c 的长度。那咱们一起来算一下。在直角三角形 a、 b、 b、 c 中,我可以通过勾股定理来求一下。 b、 c、 b、 c 等于根号下十三方减五的平方,它是一个勾股数,所以就等于十二米。在直角三角形 a、 b、 d 中,已知一个边和一个角,所以它满足可解条件。 探证的角 a、 d、 b 就等于探证的十三度。我们知道探证的角 a、 d、 b 呢,等于 a、 b 比上 b、 d 的值, a、 b 呢,它是五米。探证的角 a、 d、 b 呢,等于探证的十三度。所以想求 b、 d 的长度很容易了。 b、 d 就等于 a、 b、 b 上探针的角 a、 d、 b 就等于五笔上探针的十三度。用五米去除,以这个零点二三一,我们可以得到它约等于二十一点六四五米。 弟弟知道了,并且呢, b、 c 知道了,所以你的 d c 就等于 d, b 减去 b, c 就等于二十一点六四五,减去十二等于九点六四五, 约等于九点六米。因为题目中要求保留一位小数,所以斜坡改进后, d 与原骑士点 c 的距离就为九点六米。 我们看一下啊,不管是第一问还是第二问,我们都将一个实际问题呢,转化成了数学模型,变成了解直角三角形的问题。在解直角三角形的时候,你要判断啊,已知两边是否可解,已知一边一角是否可解。 总结一下这个视频,我们学习了坡度,坡度也叫坡比,它表示的是坡面的垂直高度 h 与水平宽度的 l 之比,用字母表示为 i 等于 h b l。 当你知道坡度的时候,就可以知道碳真的 alpha 的值,因为碳真的 alpha 等于对比零,也等于 h b l。 坡角呢?坡角是坡面与水平面的夹角,这个夹角记住 alpha。 我们在 解决实际问题的时候,常常将实际问题呢转化成数学模型,然后通过解执照三角形的方法,就可以解决这个数学问题,从而解决我们生活中的实际问题了。你学会了吗?
187梦斯老师 02:00查看AI文稿AI文稿
02:00查看AI文稿AI文稿case 中坡度的定义和计算方法?在 case 中计算土方或进行放坡时,常常需要用到坡度,这个参数如下所示,在土方计算中需要用到坡度。 在 case 中坡度定义为坡角的正确值,如四十五度的坡应该输入为一比一。若只知道坡降和平距,该如何计算输入坡度呢? 如下,三角形中对坡将平距等进行了标记,此处坡角是指 坡面和水平面的夹角,坡将是指坡顶到坡底的高差, 所以计算过程为,一比坡度等于坡降除以平距,坡度等于平距除以坡降,坡度即为 case 软件中坡度处的输入值。如下面的实力, 若设计图上只标注了坡顶和坡角高层及放坡方向,可以采用下面的步骤进行计算。首先利用工程应用菜单下差距两点的距离, 以获得坡顶和坡角的平距为二四点零幺三米。接着计算坡降等于坡顶高层减,坡角高层等于四零点二五减三,三点幺二等于七点幺三。故坡度等于平, 除以坡价等于二四点零幺三除七点一三等于三点三六七九。 在进行输入的时候还要注意是向上放坡还是向下放坡,以免发生错误。以上计为 case 中坡度的定义和计算方法。
767测绘二哈 08:19查看AI文稿AI文稿
08:19查看AI文稿AI文稿今天呢和大家聊一下坡度,昨天呢直播间就有人问到坡度这个事,今天呢再和大家说一下,老同学呢,听过的就当是复习一遍。先说一下呢,施工过程中经常能遇到的坡度表示方法呢,就是常见的形式呢,大概有三种, 一个呢是比例法, 还有呢是百分速法, 最后一个呢是度数法, 不管图纸中给出我们这是这三种方法中哪一种都是呢,万变不离其中, 大家呢要以不变应万变, 坡度计算呢,大家要掌握的一个原则呢,就是记住一个核心公式,就是坡度呢等于是高度比长度, 高度呢就是图,从图中呢找他的垂直距离, 长度呢就是找他的啊水平距离。我们呢先看一下比例法, 比例法呢,一般运在什么地方比较多呢?一个是基坑开 八, 还有一个呢就是坡道, 这两个地方呢,通常呢用的坡度表示方法呢就是比例法,坡道呢又可以细分常见的坡道呢,第一个无障碍坡道,大家呢也俗称为残疾人坡道。第二个呢就是 自行车坡道,也是非机动车坡道。第三个呢就是汽车坡道,这几个地方呢用的一般呢都是比例法,我们举个例子,就拿鸡坑开挖来说,比如说呢,挖土的深度呢, 十四米,按一比零点七来放坡,可能挖土四米,那可能大家都 不太好理解我,假如呢就挖一米,我画个示意图, 挖土深度一米,还是按一比零点七来放坡呢?他的垂直距离呢,这个地方的距离呢就是一米 放坡坡度呢是一比零点七,怎么理解呢?大家记住刚才的公式,坡度呢等于是高度比长度, 高度呢就是这儿的挖深一米,长度呢就是这儿的放坡宽度,也就是说呢就是上口跟下口的水平投影距离,就 就是不管你用什么方法,我抓住的核心呢就是高度比长度,所以它的长度呢,这是 x, 一比零点七等于一米,比多少呢是零点七米。 我们呢再回到提议,他要求呢挖土深度是四米,那么这呢需要换成四米,那么呢挖一米需要放坡宽度呢是零点七米,那么挖四米呢再乘个四二点八米,这呢就是比例法。 第二个要介绍的呢就是百分速法, 百分速法一般用在什么地方呢?一个是屋面找坡,还有呢是窗台压顶,大家要 记住窗台压顶呢,是由屋里向屋外找坡, 这是外,这是里。还有一个就是女儿墙,女儿墙的顶部, 女儿床的顶部呢,是向屋面找破,就是由外向里找破这个方向呢,大家要记住 我们举的例子呢,我们呢是拿屋面来举例子,假如呢屋面找坡,他的坡度呢是百分之二,我们还是画个图, 五秒钟 老婆,百分之二呢,其实呢他百分之二呢,虽然他是个百分数法,其实说白了百分数呢也是一个比例法,就等于呢二比一百,他跟比例法呢是一个意思,我们还是抓住,不管你用什么方法表示坡度,我都记住一点,就是高度 比长度, 所以说呢,高度呢就是垂直距离,这个距离呢就是两米, 这个呢就是水平,距离呢就是长度就是一百米。如果从图中呢给出来,我们从图纸中看出来,这个距离呢是二十米, 那么呢,这个水平距离呢,就是二十米,那么高度怎么求呢?拿长度乘以百分之二,也就是说 高度呢,等于是零点四米,也就是四十公分,就是说最高点跟最低点的投影距离呢,就是 四十公分,这个呢就是百分数法。百分之二的含义,也可以说呢,你也同样可以换成比例法来,是一个意思,就是百分数法呢,它的本质呢就是比例法。最后一个要讲的呢,就是度数法。 杜住法一般用在哪?是脊嘴坑 挤水坑这个地方呢,运的比较多,他 他呢不管集水坑,比如说给了我们的一个角度呢是阿尔法,其实呢,他的阿尔法呢,可以换成正切贪正的阿尔法,等于呢高度比长度, 高度呢,同样是垂直距离,长度呢就是水平距离。我们画一个积水坑, 脊嘴坑的坡度呢,一般呢,常见的就两个角度,一个呢是四十五度,一个呢是六十度。 假如呢,我们这个角度呢是四十五度,他的贪正他二法等于一比一,所以说的角度法换成比例法呢,就是一比一,他呢也是找高度高, 高度呢是这个深度,这个长度呢就是放坡的啊宽度,所以呢,高度呢 比长度呢等于一比一,他俩呢是相等的,这两个边呢就是相等的, 这个呢就是度数法。度数法呢,同样根据正切来求呢,也可以换成是比例法,也就是说呢,坡度一点都不复杂。 其实呢,这三种方法说白了就是表示的是同一个意思,只要呢,大家把这个坡度等于高度比长度呢这个核心公式掌握了,不管你用哪种方法,爱谁谁,我就知道这一个点就可以了。如果大家还是弄不清的,可以在评论区留言。
4380砼韵教育咨询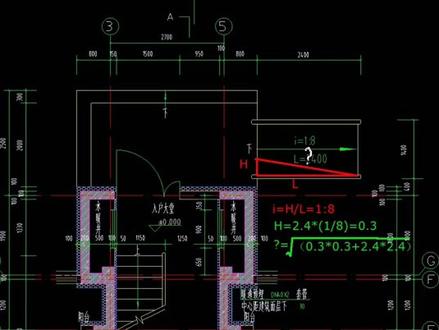 01:21查看AI文稿AI文稿
01:21查看AI文稿AI文稿图纸中的符号坡度,在图纸设计中我们经常可以看到坡度的表示,比如我们现在看到的坡道,以及我们在道路的施工图当中可以看到路面的一个找坡方向,以及呢在屋面图纸当中,我们也可以看到他的一个坡向, 那么我们经常看到的坡度表示有两种,一种是比例方式,还有一种是百分比的方式,都以箭头来代表他的一个坡向, 那么我们在这里画一个三角,这个位置是 h, 那么水平方向的话是 l, 坡度 i 等于坡角的对边, h 边比上零边 l 也就等于我们现在在图纸当中所看到的一比八的一个关系,所以这样的话,我们就可以根据图纸设计当中所给出来的数据值来计算我们所需要的数据。 那我们看到这个坡道他的水平向距离是两米四,那么水平向为两米四,也就是 l 方向为两, 那么我们可以根据他的坡度比值来计算出他的斜向长度,那么很简单,我们可以根据坡度来计算出 h 的值, h 等于 l 两米四,二点四米 乘以一比八,这样我们就可以计算出来 h 的值,那么算出来结果为零点三,那这样我们就可以计算出来斜长 鞋长,可以通过勾股定理的方式来进行计算。
157一砖一瓦造价培训 03:20查看AI文稿AI文稿
03:20查看AI文稿AI文稿哈喽,大家好,今天和大家分享学到的角度和坡度之间的关系。也是前两天有个朋友来问我怎么去计算,如何去计算,我就把一八年的一个知识图给大家翻了出来, 在图片的红色呢,我们看红色的字,等号右边呢是雪道的角度,等号左边呢是这个角度所对应的坡度。 例如四十五度的雪道呢,他的坡度呢,对应了就是百分之百。坡度的计算原理呢,就是 雪道的角度对应的那个垂直的高度,坡的垂直高度和他的水平的距离的一个比值就是坡度。那么为什么四十五度的雪道的坡度是百分之百呢? 这个里面就设计到了一个数学公式,叫三角函数,就是视频里面的 t、 a、 n 括号角度。他的意思呢就是说一个角度所对应的垂直边和水平边的一个笔直。 我们用这个图来进行举例,角一呢就是雪道,他的角度, a 边呢是这个角的零边,就是他旁边的这个边,也就是他的水平距离。 b 边呢是他的对边,是这个角的对边,是这个雪道的垂直高度, 所以这个雪道的坡度呢,就等于摊间的角一,也就是等于他的对边比上他的零边,也就是 b 边比上 a 边。我们用四十五度的雪道来进行举例,因为三角形的 角盒是一百八十度,如果有一个角是九十度,另外一个角是四十五度,那么另最后一个角也是四十五度,所以这个三角形呢,就是一个等腰直角三角形。那么也就推出了 b 边和 a 边的长度是相等的, 我们进行这个公式的套用,所以坡度呢,就等于摊径四十五度,也就是等于 b 边比上 a 边,由于 b 边和 a 边的距离相等,所以呢,他的比值就是一,那么乘以百分之百呢,就是百分之百。 有朋友问了,那我去计算一个雪道的坡度,难道要去真正的去量他的垂直高度和水平距离吗? 其实是不用的,因为只要学到的角度不变,他的坡度也是不变的。最简单的方法呢,就是你直接去百度里面去打探近的十度啊,他就会给你出来一个结果,你乘以百分之百就行了。比如这十度的话,他 对应的就是百分之十六点十七点六的一个坡度,你去打三十度的话,然后他就是百分之五十七点七的一个坡度。如果是四十五度的一个雪道的话,他的一个坡度呢,就是百分之百。 但是在实际的这个情况中,雪道他不可能是完全平的嘛,所以他,呃,有些地方呢,坡度可能会大一点,有一些地方坡度会小一些。在实际的滑行中呢,其实肯定没有人去算这个数字的, 一般就是你要去划黑道,就是所谓的高级道,你肯定就是要留神或者注意了。比如北京南山的,他后山的那个道的话,应该是三十几度,嗯,类似,呃,还有的话就是万隆他大波头的话,应该也是三十三四度吧。
515滑雪教练情报站 02:21查看AI文稿AI文稿
02:21查看AI文稿AI文稿坡度怎么计算?在建筑施工中,我们最常见的坡度表示法一共有三种,分别是比例法、百分数法和度数法。 坡度的表示符号共有四种,这是比列法,这是百分数法,这是度数法。还有这个爱等于多少,这个就是坡度值的表示符号。什么是坡度?坡度就是高度比长度,高度就是找他的垂直高,长度就是找他的水平宽。下面我以比例法中的放坡比给大家举几个例子。 比如说这是一个基坑开挖挖三米,他的坡度表示法用了一个三角形,上面标注一比零点五,怎么理解这个一比零点五,比如说这里这个三角形 就是这里这个三角形,这个一比零点五中的这个一就是这里的一米,这个零点五 就是这里的五十公分。意思就是这个鸡坑挖深一米需要放宽五十公分,他要挖三米深,那就乘以三等于一点五米。意思就是这个鸡坑挖三米深,需要放宽一点五米。比如说这是一个公路的两面放坡, 坡度是一比一点五,怎么理解?这个一比一点五,意思就是这个公路一米高的时候需要放宽一点五米。 现在公路的高度是两米,那就用一点五的宽度乘以他的高度两米,等于放宽的长度三米。在这里大家要注意一下刚才说的这两个,有很多人会把一丝想反掉。坡度是高度比长度,高度就是垂直于地面的高度,长度就是平行 于地面的宽度。比如说这里这个蛙三米深和这个高两米,他们都是垂直于地面的高,这个五十公分宽和这个一点五长,他们都是平行于地面的宽或长, 只要记住坡度是垂直高比水平宽就不会出错了。刚才讲的这两种算法只是比例法中求水平宽算法, 如果比例法用在上升或下降的地方,那么他的算法就和刚才的算法就是完全不一样的。同样百分数法、度数法,还有这个爱等于多少,怎么理解和怎么计算,有想学的可以点击左下方视频观看详细内容。
156工匠之家巧计算 00:45查看AI文稿AI文稿
00:45查看AI文稿AI文稿大家好,在看我们土方进行放坡时,都能看到相应的放坡系数,比如这标的一比零点五, 那一比零点五是指的哪块的和哪块之间的一个对比呢?对于坡度来讲,考虑的为 h b 上 l 的,那 h 指的哪一块呢?就代表的是高度, l 呢?相当于水平长度 l 所形成的笔直即为坡度一比零点五,同样的这一块也是这两个数据的一个对比,大家了解了吗?
771市政工程造价易老师









