2026黄浦一模立体几何
粉丝2437获赞5922
相关视频
 37:264089数飞飞
37:264089数飞飞 02:53
02:53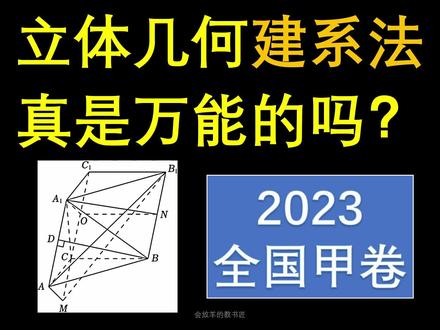 14:41查看AI文稿AI文稿
14:41查看AI文稿AI文稿大家好,今天我来讲一下二零二三年全国假卷的立体几何大题。通过这道大题的讲解,我其实想告诉大家一个道理啊,就是间隙法在立体几何大题中真的不是万能的,很多立体几何的大题,其实不能用间隙法或者用间隙法,它的计算量太大 来,真正聪明的同学啊,应该是立体几何,他的间隙的方法还有纯几何的方法都应该掌握,都应该灵活运用。我们看一下这道题,他说的是三棱柱中,这个三棱柱的话,他可不是直三棱柱,他这个侧棱是斜着的啊,这一看就能看出来, 然后呢,继续往后读,他说什么呢?他说的是 a a 一等于二,就是侧棱长啊, a a 一, b b 一, c c 一其实都等于二。他告诉你谁垂直于底面呢?他说的是 a、 e、 c 这样一个侧面的面对角线, 它是垂直于 a、 b、 c 这样一个底面的,它垂直啊,并且告诉你这个角,也就是说 a c 和 b c 夹角是九十度吧,也就是说什么呢? a e、 c a c、 b c 这三条线两两之间是互相垂直的,可能到这之后的话,很多人就直接 x 轴、 y 轴、 z 轴写上了。这第一问肯定不是这样来正的啊,根本就没有必要去间隙,不是用间隙法来做的。那么我们看一下 它最后还有一个条件, a 一到平面,它的距离是一。我呢,反正读完题之后,我就看到了一个一,一个二, 反正再加上两个垂直呗。好,一二垂直,那你能不能想到在直角三角形中,斜边中线等于斜边一半这样一个一比二的道理啊?肯定能吧,那么我们来看一下 这道题啊,第一问的话,真的特别简单,我们就找重点啊,斜边重点等于斜边一半,哪个平面呢?我们把这个侧面啊,也就是 a e a c c e 这样一个平面呢,他这个侧面画出来他的平面图,画完这个平面之后的话,首先垂直底面,不用多说了吧, 既然你这个 a e c 是垂直于整个底面 a b c 的,它肯定垂直于 a c 啊,那进而也垂直于 a e c e 啊,是不是?好了,肯定这个垂直是好得出来的,得完这个垂直之后的话,为什么要找终点呢?首先斜边中点的一些密码,这是二吧, 这是一吧,点 o 在哪啊?你要注意啊,在这样一个立体几何的原图中,这个点 o 它指的是 c c 一的终点,那么点 o 它记在 c c 一上面,那肯定就是在平面 b c c b 以上的。好了,不用多说了,看好了啊,因为什么我们分析一下这道题,很容易证明呢?这个 a e c 是垂直于 a e c e 的, 并且呢,再来看这个 a e o 斜边中线等于斜边一半吧,它就是斜边 c c e 的一半,等于一啊, 那么既然点 o, 他是在什么?他是在平面上的,我知道了,其实你看了啊,因为 a 一点到,请告诉我,在初中阶段学过这样一个定理,没有点到直线,除以现在最短吧,那高中的话,我们就知道了,点到什么? 点到平面,他其实也是垂线段最短的,最短最短,最,就是唯一的意思啊,就是那个垂足只有一个的意思, 其实那个点 o, 它就是点 a 一到平面,哪个平面我写清楚啊?到平面 b c c 一 b 一的这样一个垂组,那个点 o 就是垂组,懂了吧?它的距离 我写清楚了,距离为一,所以再加上什么,所以我就知道了呀,其实 aeo 它就是垂直于整个平面 b c c 一 b 一的,剩下不用多说了吧。然后呢,也很容易证明的一点是什么?也很容易证明的一点是,首先我们可以通过证明谁通过证明这个 b c 垂直于整个 侧面 a c c 一 a 一,然后进而证明两个平面,也就是说平面 a c c 一 a 一,它是垂直于我们的 目标平面 bccebe 的。为什么呢?原因很简单,首先我已经分析过了,两两之间互相垂直吧,既然他这样一个 bc 垂直于平面里头两条相交直线,所以就垂直于整个平面,进而呢,就得出来这样一个面面垂直了,那得出来面面垂直的话,你说这两个平面 它的胶线是谁啊?这肉眼可见的嘛。胶线,两个垂直,平面的胶线就是它垂直于胶线则垂直,平面,垂直于平面则垂直于它俩的胶线吧,这是一个定力点,所以其实 a u 它是垂直于整个 c c e 这样一个胶线的。 那既然证明完这一条的话,所以不用多说了吧。点 o 既是垂直的,它也是终点,所以 a u 是什么?是中垂线呀?中垂线它的性质定理是什么?中垂线上的点到 线段,两个端点距离相等,所以它这个 a e c 等于什么?就等于 a e c e 啊,那 a e c e 显然是等于 a c 的,不就证明完了,就这么简单, 懂了吧?点到平面垂线呢,最大它的距离就是一,这道题给的太明显了,一个二,一个一,加上两个垂直,肯定是要想直角三角形中斜边中线等于斜边一半这样一个定律的。我们继续来看第二问啊。第二问的话,如果你要选择用间隙的方法,不是说不能做,我说一下 间隙的方法有什么缺点啊?间隙的方法的话,咱们根据第一问这个图形的话,很容易判断这个 a e c 和 a c 它的距离的话,肯定是等于根号二的啊,这个都很容易算,也就是说 a 一点,还有 a 点我们坐标呢,都是可以写出来的, 然后包括这个 a 一点,我们可以写什么?那 z 轴当然是零,逗号零,根号二了,但是 你想写 b 点吧, b 点的坐标你得假设了,只能假设零多少 t 零,你还得把这个 t 求出来。根据线与线的这样一个距离, 是不是还得做辅助线,比如说 b 点啊,做了一个垂直,比如说垂直于他,然后 bh 的长度是等于二的,然后再进而用什么用 啊?要么是点臂到向量的距离公式,要么就是根据平面向量他这样一个投影的公式,当然 他这个空间下来也可以用投影公式啊。所以说这道题的话,剩下的计算量会很大,然后再把这个 t 具体的话是等于根号三算出来。这个咱不推荐这种方法,你看看如果这道题 用纯几何的方法,他有多简单啊。看了,首先这道题的话,有一点很明确,你看刚才我们在证明的时候,这个 aeo 是不是垂直于整个平面点好, 这道题的话,我连接一下 a b 一,为什么连接这个 a b 一呢?道理很简单,因为你求的就是 a b 一和整个目标平面的它夹角的正线值。这个平面的话不用多说了吧,我就擦掉了啊,平面是在这样一个位置的,在后边, 那么看线面角,它的平面角需要找出来。其实线面角它得有三个要素。首先第一个要素就是 就是斜足,斜足就指的是斜线 a b 一和平面的焦点,斜足当然是 b 点了,不用多说,斜点的话是我发明的这样一个名词,其实就是斜线上的异于斜足的一个点,那就写成 a 点, 没他有这样一个点过, a 点还得做出些什么,他其实缺少了。第三个要素,缺少了垂足,对吧?比如说我们做 am 是垂直于整个平面哦,所以当你想到这一点的时候,我觉得辅助线其实就很明确了。首先第一条辅助线我先告诉你啊,我们只需要做 am 怎么样? am 是平行于 d 问中的 aeo 的,他俩之间是平行的呀,再加上别的平行交臂啊。知道了,那有了这样一个平行之后的话,再加上这个 aae 是平行于 cce 的,肯定很容易出现一个平行字边形吧。咱们写上啊, 这个平行四边形呢,就是 a m o a e 能得出来,那根据平行四边形结论的话,是不是很容易就得出来 a m 的长度了呀?它和 a u 的长度其实都是等于一的, 对不对?那做完这个之后的话,效果是什么?你为什么要做这个 a m 平行于它呢?道理很简单,因为在第一文中我们已经说明了 a e o, 它就是 下面垂直的那样一条垂线,它是垂直于整个目标平面 b c c 一 b 一的。所以既然平行的话,你这个 a m 是不是也垂直于整个平面 b c c 一 b 一啊?它想告诉你的就是说 m 点, 他就是线面垂直的这样一个垂足呀。得出这个垂足来之后,你看线面角的三要素都有了啊, a m 是整个平面 b c c e b 一他的垂足吧,点臂是斜足,他是,哦,连接起来我知道了,如果我再说的明 这些,其实就是这么的回事,这是 a 点,这是 m 点,这是 b 一点,那这个 am 等于一。已经算出来了啊,它的长度等于一,那么其实我们只需要算一下 bm 或者说啊 ab 的长度就行了。 这道题我们选择算一下 b、 e、 m 的长度,是不是就把这个正弦值算出来了呀?因为这道题,他这个线面角的平面角其实就是垂啊,我写出来他这个线面角的平面角,其实就是让我们求哪个角,求这个角 a b e m 它的正弦值,显然它的正弦值 a b e m 是等于谁比上谁了,你就告诉我,其实就是等于刚才我画的那样一个直角三角形 a m b e 中的它这样一个 a m 的长度,再比上谁的长度,再比上 a、 b、 e 的长度, a b e 长度的话,我觉得不太好算啊, a b 是斜边,我们就用勾股定理来算吧, a m 显然等于一, 它下边这个斜边。关于这个 a b 一的话,我们就用这个 a m 的长度的平方,再加上 b e m 的平方。所以这道题其实我们只需要算,是到现在为止我分析清楚了,只需要算 b e m 的长度啊,你既然要算 b e m 的长度的话,是不是要涉及到勾股定理啊? b e m。 好,现在看了 b e m 可以放,把它放到哪个直角三角形中看了, 这是不是一个直角三角形?我们分析一下,肯定是直角三角形的吗?其实后边的话,他这个平面你看看好了啊, bc 是不是垂直的?是啊,垂直于 cce 啊,所以后边这样一个平面,他其实是一个矩形的, 对吧?这个很容易得嘛,根据九十度,根据垂直就可以得出来矩形。矩形的话来看,是不是需要先求一下 b 一 c 一的长度,再求一下下边?我觉得不用多求了吧,肯定很容易求出来的啊。我们容易得到的是, 其实有一个全等的,谁呢?三角形 a m c, 它是全等于三角形 a e o c e 的,你这个 c e o 的长度等于一点二,是终点吗?它的长度也是一,所以下面这个 c m 的长度, 它是不是就等于这个 c e o 的长度等于一?它都是一啊,所以我这个 c e m 的长度就等于一加一加一等于三就算出来了。关键在于我这个 b 一 c 一是多长? b 一 c 一。好,第二条辅助线看好了啊,第二条辅助线要干嘛呀?要找一个 b e c e 的终点,因为点 o 已经是终点了,点 n 也也是终点那 o n 的长度,哎,能理解吧。看了啊,千万不要着急,这道题首先看好了。 嗯哪呢,我要换一种颜色吧,千万不要混了看。首先, c c e 它是怎么样的?它是垂直于 a e o 的吧。第一问已经解决过了, 并且呢,根据矩形的特性,这个 c c e, 它也是垂直于这个 o n 的吧?你垂直 c c e, 垂直于整个平面里头两条相照直线,它不就垂直于整个平面 a e、 o n 吗? 所以进而就推出来,这个 c c、 e 是垂直于整个平面里头的最后一条线。垂直于谁?垂直于 a e n? 当你求完垂直于 a e n 之后的话,你这个 a、 e、 n 是不是垂直于 b b e? 来看看 看啊,新增那些条件,括号二,增加了个什么条件?他说这个 aae 和 bb 这两条平行线之间距离就是二,那不就是点 ae 到 bbe 的距离,这个 aen 不就是那个距离等于二吗?对吧?根据已知条件,这个 a、 e、 n 的长度,根据垂直,他就是两个平行线 a a 一和 b b 的距离等于二。好了,剩下呢,不用多说了吧,所以能算了啊。好,我把剩下的东西呢,该擦的都擦掉来。 a e o 等于多少吧?等于一吧。然后呢,这个 a e n 等于多少?等于二吧。那你说这个 o n 等于多长呢? o n 肯定是等于二的平方减去一的平方。勾股定理啊,它是等于根号三的, o n 等于根号三,所以说 b 一 c 一其实也是根号三,所以 记得很清楚啦, b e m, 它的长度是等于根号下 b e c e 的平方,再加上 c e m 的平方, b e c e 的话,平方就是三,这个 c e、 m 的平方就是九,对吧?三的平方等于九,等于根号十二二倍根号三呀。 那么我们要算的最终的结论不是就有了吗?刚才在这样一个位置我已经写过了这个三角 a b e m, 它是等于谁比上谁的,它就是等于这样一个直角边 a m 比上斜边 a b 一的其实也好算啊。那 a m 的话就是一它的平方啊。根据勾股定理,这个 a b 一,它是等于 a m 的平方,其实就是一的平方,再加上谁再加上这个 b e m 的平方吧。那显示等 等于十二点,最终结果就是根号下一加十二,根号十三分之一,也就是说十三分之根号十三就解决完了。所以这道题的话,其实我主推的方法是什么?就是几何的方法。当然,如果你真的要用间隙的方法也能算啊。也不是说不能算,那么真正 聪明的同学是立体几何,间隙的方法也得掌握。还有立体几何纯几何的方法也得掌握清楚了吧。分享课堂知识,感受数学之美。我是安分老师,下节课再见!
4274会放羊的教书匠
猜你喜欢
- 2.3万落空桥















