matlab中fmesh函数怎么用
今天主要介绍一下 matlab 的一个蜂蜜克函数去求解一个无约束的非性性规划啊。当我们去求解这个没有约束的非性性规划的时候,就比如说他的目标函数是非线性的,那这时候的话可以使用这个蜂蜜克这个函数去进行求解 啊,这个函数的话可以求解无约束多变量函数的最小值,嗯,他可以找到指定问题的最小值,然后主要是就是啊求函数的最小值,然后这里面的 x 的话,他可以是一个一个变量或者是多个变量,他是他可以表示一个变量的一个向量或者是变量的一个矩阵, 然后这里面的这个蜂蜜靠的这个函数的话,他的语法的话用的比较多的是,比如说他的第一个速度是这个目标函数,然后第二个是函数的一个初始值,就是呃变量的一个初始值。第三个速度参数的话,就是可以对他设置求解器的 一个相应的一个参数,就比如说这个最大的迭代次数以及相应的一个算法。然后如果是我们要获得对应的取得最小值的一个函数值的话,那我们就可以返回两个输出参数,两个输出参数, 那这第二个输出参数的话,就是表示的是呃这个目标函数取得最小值, 然后这里的一个呃,如果是输入输出三个输入参数的话,那这第三个输出就表示的算法的终止标志。就比如说呃你这个通过这个求解器求解的是比较离呃这个 最小值点还是近视的最小值,还是没有求出来。然后如果是有四个输出参数的话,就这个第四个的话就表示的是返回优化算法的一个数据结构,然后第五个如果是有第五个输出的话,第五个的话 就是表示返回目标函数在最优点呃最优减 x 点的梯度。如果是有六个的话,那对应的最后一个第六个这个输出参数的话,表示的是目标函数在最优节点 x 点的一个函数矩阵。 然后这里面的话可以为这个呃这里面这个修写器的话提供了两种啊,对大型的优化算法和中型的优化算法,它提供了两种的这个呃 两种选择。就比如说如果这个 logical score 为 on 的话,默认是打开的,那就它会使用大型的算法 lose off 的话,它就会默认使用这个中型的优化算法 的搜索方向。提供了四种算法,比如说这里面的 b, f, g, s, 然后 d, f, p 或者是 这个呃转速下降法, 然后主要以一个以几个实力来讲解一下,就比如说这里面的话是 f 的话是关于 x 一 s 二的一个呃非线性的一个目标函数,因为它里面还有平方向交叉项,那这时候的话我们进行求解的时候,就是看 s 一 s 二取多少的时候,它对应的函数值最小, 那这时候我们可以看到这里面没有规划,没有没有那个约束吗?那这时候就可以就可以用这个啊,蜂蜜口 啊这个函数我们进行求解,我们可以看一下这里的一个运行程序,首先的话这个是要随时清除命令行窗口,以前的这个命令,这个零二的话是清除工作区的一些变量, ctrl 的话是关闭一些以前的图形窗口,那这里面的目标函数的构建的话,我们可以通过匿名函数的 形式区进行构造啊,那我们可以看到这里面的话是通过这个匿名形式艾特括号 x, 那就是表明 x, 它是其实上是一个变量。变量的话,我们这里面的话有 x 一和 x 二, 那这时候的话就是三倍 s, 括号一的话,那就表示 s 一,以此类推,那这里的话是三倍 s 一平方加两倍 x 一乘以 s 二加二十二十二十二的平方减四倍 s 一加五倍 s 二,那这时候的话就把对应的 啊目标函数写成对应的一个程序语言,那就是三倍二十,括号一的平方加上两倍二十一,乘以二十二,加上二十二平方减去四倍二十一加五倍二十二, 那这时候的话就是通过匿名函数的形式将这个呃函数写成了这个目标函数,那这里的 x 零的话就是初始点,我就随便取了一个一,那这时候我们进行 运行,我们可以看到用的是二输入,二输出,那这里的是第一个输入是这个范,是这个函数值 s 零,是函数的一个初值。呃,求解的初值点,那这时候返回的是 x 和 few 啊,这个 s 的话是二点二五和负四点七五, 然后这里返回的最小值是负十六点三七五零,那这时候我们可以看到他找到的是这个局部的最小值被发现了,这就是一个简单的一个例子, 然后这是程序和运行接工,然后第二个例子,我们可以看一下,这个例子的话,它也是管两个多元面量的非线性函数,里面是包含了指数函数和它的一个平方向,所以的话是非线性的,非线性它没有约束条件,那这时候就可以用这个蜂蜜一看来,呃蜂蜜一口子来进行一个求解,那这时 之后的话,我同样的我们可以通过这个程序来看一下,呃这个程序的话 一,嗯嗯啊,在这里这个程序的话应该是在这里 啊,这个程序的话是这个啊,也是通过这个前面三行是和前面程序是一样的,然后这里的话就是啊把对应的也是通过匿名函数的形式 定义的这个目标函数,在这里的话就是把这里的啊目标函数转化成程序语言。二十一乘以一的负二十一平方加二十二平方,加上二十一的平方,加上二十二平方除以二十,可以看到这里和 这里一样的啊,这时候这个 option 的话就是我们可以去设置这个蜂蜜口的这个呃求解器,呃它的一个参数属性,首先第一个输入的话,我们可以通过这个 op, op optimi 哦, options 就可以设置。首先是第一个是我们要对哪个球鞋进行一个设置,然后这里我们可以去设置它的呃方向为 d f d f p 方向啊。 display 也就是它的一个迭代的次数的一个计算过程,我们可以呃让它这个 display 呈现, 然后最大的迭代次数一般默认是四百次,我们可以设置大一点一千次。然后我们可以去把那个求解的过程把它的这个啊随着迭代次数的变化的一个函数值的变化啊,把它绘绘制出来,然后这里我们就把这里的通设置好 参数复制给这个 option。 然后我们这里的 s 零的话就是初值,因为它有两个变量,所以是一二,这随随便取。然后这里面的话会有六个输出,我们可以看一下这里面的这三个输入的话,就是目标函数初始点和这个呃九九七的参数设置,我们可以运行一下,我们可以看到 啊,首先的话他这里会出现一个迭代的次数的一个过程的一个图啊,横轴的话表示的是迭代次数,重轴的话表的是函数值,我们可以看到当前函数值是负四点零五二三七。 然后我们可以看到这里面的话,首先这是个命令行,这里的话会有一个迭代次数,也就是我们设置的这个啊 display int 就是啊迭代次数对应的这个函数值,还有就是它的一个连续 呃它的一个这个一些信息。然后面的话就是求解的这个六个输出,首先是 x 等于负零点六六九一和负零,那这时候就是表示 s 一取负零点六六九一, s 二取零的时候有这个局部的一个最小值, 然后这里最局部最小时是负四点零五四零五二,他他这里有返回的标志为一,一的话就是表示呃求解的比较好,然后这里面包含了这里面的一个参数, 就叠带了九次,就是包含了一个结构点,然后 grid 的话就是呃这个目标函数在这一点的这个梯度,然后这个函呃函数在这里面的函数在这一点就是在这个二十一等于负零点六六九一二十二等于零,这一点的一个函数矩阵。 好,这是程序和运行结果。第三个实力的话就比较简单了啊,也是两个变量, f s 一 s 二,它是关于三倍 s 一加平方加两倍 s 一乘以二十加二 再加 s。 啊,那这时候的话我们也可以通过怎样呃,我们可以通过制定函数的形式去把它改写成目标函数。呃,首先的话我们可以看一下这里面,嗯,这个, 呃,首先的话前面三行是一样的嘛,这 s 零是起始点,然后通过这个 option 的话,我们可以呃,刚刚的形式的话是这个字字里面是点,那个,呃,单引号里面加蜂蜜卡,同时同样的我们也可以这样去呃,这样用这个蜂蜜, 你看,呃,就是,呃,就是通过这个艾特,艾特这个否,我们一看我们就是可以通过这里设置二四零的话是提示点,可以通过这个 o o t o 选择,可以设置设置它的长按数点代的次数为输出最大点代次数, 还有这个输出。呃,绘图的他的一个年代是不是随着这个函数值的变化?同时的话我们可以看到这里时候的话,第一个呃,冯米克的这一个输入参数的话,是通过这个艾特艾特话就是调用的这自定的一个函数文 我的一个形式,那这里面的话就是发选制定了这个埋范为他的一个目标函数,然后里面的话就是三倍二十一平方加上两倍二十一乘以二十二加二十二的平方,那这里的话这个 f 的话就是他的一个输出,那这时候的话我们实际上是可以看到,嗯, 这里面的就是通过这个艾特,艾特就是自定函数形式去设置 x 零是初值,这里是,呃,这个,呃求解器的设置,我们可以看到同样可以看到它的一个函数的迭代的次数和这个函数值之间关系以及它的一个输出。 可以看到,那这里的时候,这里的 s 一和 s 二都是一乘以十的负六次方,这里是零点二五乘是一乘以十的负六次方,这是负零点二零二九乘以十的负六次方,那实际上这两个值就相当于零零,也就是说当 s e s h 零零的时候,这个函值去啊最小值,那这时候的话也比较符合他的一个理论的分析。那这里的话是通过另一种就是制定函数的形式去 调用他的一个目标函数,然后这里是程序和运行的一个结果。第四个例子的话,实际上他也是一个两啊多元的一个分线性的一个约束的规划,那这里的话目标函数就是一百乘以二十二减二十一的平方,加上一减二十一的平方。这时候我们就看一下这个程序的话, 嗯, 呃,这个程序的话我们可以通过,嗯, 啊,这个程序的话,在这里前面三行是一样的,我们同样就可以对它进行一个设置,然后这里面的泛一的话,我们是也是通过调用的自定函数的一个形式, 然后这里面的是目标函数,这是对应的一个 呃梯度,然后是通过这种方式进行一个呃,把它设置为这个目标函数,呃,然后在 s 零这个 option 我们可以运行一下,看一下, 同样的也会返回它这种迭代的过程,可以看到这里是迭代次数比较多,对应的一个结果,这是对应的这个迭代的次数啊,同样的我们 这是对应的一个程序和运行结果,同样的我们也可以去 使用结构体去调用这个蜂蜜克这个函数的求解器啊。结构体的话我们比如说是可以这样去进行一个求解,然后我们这里是前面三样是一样嘛?这个 option 我们可以设置这个为蜂蜜抗这个求解器 呃这个算法的搜索方向 d f p 格式那个算法,然后这个呃求解的次数,最大的叠带次数和这个绘图,然后我们可以 把这个 option 设置给这个 problem 点 options, 我们就可以设置的为一个 problem 的一个结构体,结构体里面的话有 x 零这个 objection, 然后还有这个 slower, 然后这里的话我们就可以把所有的信息呃写到这个 problem 这个结构题里面,然后把这个 problem 呃作为这个蜂蜜课的这个输入,然后作为 求解的最小支点作为一个输出,我们运行一下可以看到他求解的一个结果,和和就是使用平常的这个去调用这个蜂蜜卡这个求解器的结果是一样的, 可以看到,呃,所以的话我们就是按照自己的实际需求,可以选择不同的方式去实现这个呃函数的电用,呃电用的话比较简单,主要是看, 首先是要对这个目标函数去构造,你可以使用匿名函数的形式,也可以使用制定函数的形式,其次的话要提供 提供它的一个 s 零初值,然后如果 s 零是二维的,那就是一乘以二的,如果是三维的,就是一乘三的,以此类推。那这时候如果你要去看它中间的迭代的一个次数,那这时候的话就可以去设置它的一个 option, 通过这个 o p t i m o p i btln 这个函数去进行一个设置。然后同时的话,如果是输出要要更多的话,你要获得相应的信息的话,那就可以设置多个输出。 同时的话这里的目标函数是,呃,在进行一个调用的时候,这个蜂蜜卡参数的话,可以使用这种平常的格式,也可以把它所有的内容放在这个呃结构体里面,然后这里只输入一个结构体就可以了 啊。今天主要是以一些简单的例子去讲解这个 formit 这个函数,然后谢谢大家。
粉丝654获赞4694
相关视频
 06:51查看AI文稿AI文稿
06:51查看AI文稿AI文稿大家好,这节课给大家介绍一下 mate f 当中的函数,那么大家可以看我啊,先写一个非常简单的例子, 首先点击这个加号,可以创建一个空的 m 文件,那么我们定函数的时候,首先要加一个关键字,方式 方形,后面就是我们的一个函数的输出,那么我们比如说是 y 等于,然后等于号后面呢是我们的一个函数名,比如说我们是 f 括号, f 括号当中呢是我们的啊这边量,那这边呢?在编程语言当中也称之为行差啊, 比如说我们有一个 f 一和 f 二两个变量,那么这两个变量呢,都是单独的,一会我会演示一下 什么叫做单独的,然后用摁的来表示我们这个函数来进行一个结束啊。那这里不加按的其实也没有关系,但是最好是大家养成一种习惯,习惯性的加一下按的,因为在某些呃埋头的特殊的脚本当中,是规定你必须要加这么一种按的。 那么我们比如说我们这个 l i 是等于 x 一加 s 二的。好,那我们把它保存一下, 那保存之后呢,我们这个文件名的命名也是有一个规则的,当然他这边自动会帮我们生成以这个函数名 f 为文件名,所以这里强调我们文件名和函数名必须要一致。 广州我们再来看一下 y 等于,如果我们输入一个呃,就是那一二,那他当中也有两个元素, 但是我们按一下回车之后,他会发报报错,就是一个输入参数的数目不足,这也就是我之前说的 x 一和 x 二是两个,是一个呃,单独的,单独的一个变量,所以说 不能用这种放在一个,因为数字当中的两个元素分别来啊,代替我,我们这个就是我们想当然的把这个一表示成这个一给了这个 fc, 二给了这个 f 四,这是错误的,所以我们应该这么写, 一二,这是一个单独的变量,这样的就会得到一个三,那么这是我们这个 那函数的一个基本结构。那接下来给大家看一下一个子函数, 那这里会有个子函数,子函数呢是 y 二等于 f 一,那么 呃, x 二不是 x, 是 x 三吧, 那么这边我们还要对外进一个外等于 y 二加 s, 那么这边我们是要实现的是这个三个数和 三数的相加,就是 a 和 x 二还有 x 呃,一进行一个相加,那么这边 y 二等于 x e 加上 a 来进行一个保存,可能未使用函数 f 一啊,那就是 x, 那当然这个是,这里是食餐,这里是行餐啊,可以不一样,你可以把这个改成 x 也是可以的。对于食餐和食餐和行餐,大家一定要有个区别,就是真实的带入到这个函数啊里面做一个运算的话,那么 啊他就是一个啊。食餐如果是单独的为了构造这个函数,就像我们这个第一行,他这边的 x 一和 x 二,他就是一个型餐,而我们实际上 他这就是说这个呃, x 一和 x 一二的一个负值的话,我们肯定是跟在这个命令行窗口当中,比如说我们之前的一和二才是我们的食材, x 一 x 二就是一个形菜,那这里给大家讲一下,那么大家可以看到这边这个淡蓝色 a 变成一个淡蓝色的一个字体,那也就是说在这个程序当中 a 变成了一个全局变量,全局变量 是一个格罗布类型,格罗布类型的一个变量啊,在这个函数当中,也就是说所有的子函数都可以调用这个全局变量啊,都是可以调用的, 那这是一个特点,如果非全局变了,那这个啊,是啊,无法调用的。那比如说我们把这个结结一下放到这边,那两个函数就是一个平行的结果, 平行的结构会发现这边这边说 a 并没有使用,但这边的话虽然有 a, 但是我们一经运行就会爆错啊,这里我就不另行解释了,然后就把这个放到这里,这是一个紫函数的结构,然后我们 来运行一下啊,来运行一下这个,呃,一二,那结果应该会是四,对吧? 六十四,那这是一个呃,就是写了一个子函数。在这里面接下来我们写一个呃欠套的函数的一个例子,那我们希望我们这个 f 能实现一个这个变,这个一个累成,累成哈,就是 返回的是一个 x 的一个阶层,就比如说啊,三的阶层,三的阶层应该是等于一乘二, 乘以三等于六啊,就是这么个意思,那这里我们要用到一个切套的一个例子,如果 x, 呃,如果 x 二等于一,那我也就等于二一, 其他情况下,那么啊,这边要加两个,等于作为一个逻辑判别,那其他情况下歪 就等于呃, fx 减一,然后再乘以一个, 然后我们再来用,嗯,来给这个衣服解去结束一下,然后我们来运行一下, 那他就会返回是一个六买 f 五呢?我们应该是一二三四五,应该返回的是一个一百二吧,对吧?所以说这就是一个嵌套的一个结构啊,大家看到 fx 减一好,至于嵌套的一个,呃, 就是一个非常详细的一些介绍,或者是算法上面的一些思想的话,大家可以去网上再找一下,那么这节课的话我们就呃介绍到这里,好,谢谢大家。
822我不是Matlab 47:26查看AI文稿AI文稿
47:26查看AI文稿AI文稿各位同学大家好,下面我们继续介绍迈特拉伯的使用,继续介绍他的核心内容。今天我们介绍迈特拉伯的函数, 利用 matter 软件写程序对账程序。文件我们一般分成两种类型,第一种类型呢就是所谓的脚本文件, 脚本文件,第二种我们统称为函数文件,这个区别就是说 脚本文件里面他不会出现三根线这样一个关键字, 那么函数文件他一定会有翻跟线,这样 不只是有,而且啊,而且第一行或者说第一个不是注视的行,他一定要有三个线,并且啊为啊第一行 或者说啊第一个不是注视的行, 这就是说函数文件的特征。 那么脚本文件比较简单,就是相当我们新建一个脚本,然后啊你在这里面直接写代码,用到写上二加上三,然后我们可以选择这个 啊运行,我们也可以把它保存,保存,保存的文件名只要符合定义就可以了。保存,那我们点这个运行,也可以在这个命定仓口看到这个运行的结果。 我们在这个呃平时碰到一些学生常常犯的错误,喜欢用自己的学号作为文件名来保存,比较新建一个文件,他输入啊一 加上三,想看出这个结果是不是他保存为十号,因为他的十号是十二号保存,这个时候啊我们啊这里他保存了,然后啊再点运行,他发现怎么都是十二, 是一个常见的错误,就是说保存不要成数字,如果成数字,那么他就得到了运行十二,这结果是十二了哦,对于这种脚本文件,就是他里面不含有三个线, 那么剩下的就是所谓的函数文件。函数文件一般来说,第一行是有分开线的, 对函数文件来说,我们需要清楚两两个地方,一般来说,对函数文件我们要有啊,啊,要有两个文件 来运行他,一个是所谓的函数的定义文件定义文件,第二个就是函数的调用文件,在脚本里面调用, 这个一般是在脚本文件里面吊用,或者说在命令窗口直接吊用啊,命令窗口,然后啊,对于函数文件来说,我们要求这两个文件在同一个目录下 你才能够进行啊,同一个目录下还要求这个函数文鉴明, 必须与啊,必须与文件名与函数名相同, 必须连接完成,这是我们有几个要注意的地方,下面我们来详细讲解这些内容。 对于 metal 来说,这个函数啊,你可以完全理解为像我们数学上的函数一样的,我们数学上一般来说一个函数是 y 等于 f x, 是吧? 例如说啊, y 等于正选三 ex, 那么这个就是代表函数名称,这个是质变量,这是应变量,例如说 y 等于 x 平方, 这样,那么在这里面 s 是字变调 se 变掉,结果是这样,那迈开步里面函数应该怎么定呢?我们要有两个文件文件音啊,文件音 先定义函数,文件先定义函数,那么第一行必须以翻跟线开始, 然后啊,对于这个函数来说,我们要记住它的自变量是 x, 它的函数值是 y, y 等于 f x, y 等于 f x, 那么这下面就 y 等于 x 的平方, s 平方, 那么这就是所谓的定义,这就是定义啊,函数文件,函数文件,那么使用怎么使用呢?使用我们就要在文件二里面调用,文件二里面调用,比如说我 s 复制给印, 那么我可以算 y 等于 fs, 这样就是为了吊用。那么函数应该怎么定义呢?就是这里是周围输入量或者输入参数,输入啊,这个输入参数,那么这个叫做 输出量,会输出参数。在函数定义的时候啊,那么从这一行开始以后啊,在下面我们都要把输入量当做已经知道的值,把 x 周围已经知道的比着某个数, 通过输入量去计算出位置量。外来这下面代码,我们需要把这个输出量给计算出来,输出量给计算,这是输出,已经知道这是位置,把它计算出来。好,我们演示一下这个函数的定义, 要第一函数第一行是翻跟线开始,然后我们输出量是 y, 输入量是 x, 函数名称是 f f, 那么这里 y 等于 x 平方,平方,那么我们保存,注意这个保存这里关键的地方是在于这里啊,保存你这里起的文件名,这是叫做文件名,以我们刚才这边啊, 我们刚才这边的函数名称,这是要相同的,我们刚才已经保存完了,就这两个地方是一致的, 这两个地方是一致的,那么这样我们就定义好函数文件,就是以这个开始,把 s 周围已经知道的输入量,把外作为位置量,下面函数的主体就是通过以质量把这个位置量给算出来,把这个算出来。 好,那么怎么使用呢?我们可以在命令航窗口调用它,那么调用它我们必须给 x 一个值, s 一个字, x 等一,那么我们在 y 等于 fx, 我们就可以看到这里就出现了 y 等一,但是这会出现两个 y 等一, 出现两个外等于你这只有行数路出现两个外,那么另外个原因就是在函数主体里面,这里面啊少了一个分号,而且这软件也提示我们这里确实省了一个分号。 好,我们现在不补上分号,我们也可以直接这样调用 f f 二, f 二,那么就相当于把二带入到这个 x 里面去,下面还是主体,就是把 y 给算出来,算出来就复制给 f 二,这就是相当于我们可以这样使用,等于四, 这里会出现两个四,一个是 y 等于四,一个是啊,这里 ans 等于四,那么 y 等于四呢?是在 这里面搜出来的,我们应该加上分号啊,加上分号之后不要忘了保存啊,我们再来试用调用 fo, 按向上的箭头就可以,我们看到这样就出现了,如果我们把这个函数值复制给 a 等于 fo, 那我们知道 a 就等于二了, a 就等于四, 哎,联系,这就是所谓的函数调用,那么我们在这里写的是函数名称 ffo 啊,我们一般习惯在一个新建脚本里面来调用刚才这个函数,我们知道 y 是 fx, 那我们怎么调用呢?我们一般是在这 s 等于一,对吧,我们写上 y 等于 f x 啊, 那么 x 等于 x 一等于三,那么 y 一等于 fx 一啊,那么这里都是相当于把 这个输入量是已经知道是等于三了啊,必须要确定输入量,那么韩叔给你算出这个值来,算出这个值,并且复制给外印,复制给外印。好,那我们可以运行这几行代码, 运行这代码,我们也可以把这个保存保存,然后啊运行这整个啊整个代码,我们可以看到得到结果,但是这样定义的话,我们会有一个啊问题,呃,在这里面你 s 必须是数 啊,才能平方,如果 x 是,我要求是一到三呢?一到三,对吧?那我们再调用 y 等于 fx, 我们可以看到这样运行这两行代码,那么 x 点一二三,那么 y 就出错了,他告诉你错误的原因是 s 平方不能算,那么事上我们再来看看函数的主体, s 等一二三,那么 s 就是这么一个项链,这个项链,那把这个项链带进去, 那么像量的平方,这是没有意义的,但是我们知道 y 的 x 平方是对每个 x 算,每个 x 平方应该是按元素起平方,所以这里一般要加一个点啊,代表每个元素的平方啊,每个元素的平方,这样好,那如果是这样加了点之后 啊,我们在运行,你发现人人是错误的啊,错误的,呃, 啊,这里是啊,啊,这里保存啊,如果没保存,那么人类是错误的啊,刚才这已经保存了。好,这个就是说啊,我们可以 s, 这个时候可以输入项链了啊,项链了,只有函数的意思,就是通过输入量得到输出量啊,输出量,好,我们再看几个例子, 这就所谓的函数的定义与使用,如果说我要你定义这样函数,我定义 y 等于 s 一的平方加 x 二的平方,那我们找这就是二元函数了,这二元函数,二元函数就有两个位置量,两个输入量,一个输出量,那我们可以这样定义, 我们新建一个文件,我们也是发根线开始 y 点一 f, 我们写两个 f, 有个 x 一 xo, 我们现在命名函数作为 ff 啊,下面呢,我们要通过 x 一和 xo, 我们算出这个 y 来, y, 那么等于 s 一的平方 加上 h o 这个点的原因我们刚才解释了,这个分号的原因我们也解释了,那这样我们就保存, 保存,我们啊直接就保存,不要去修改他的文件名。好,我们就可以使用这个函数,使用这个函数可以在脚本里面,我们可以搁在刚才这个脚本里面啊,使用刚才那些脚本都没有用。好,我们继续啊使用 就可以说 x 一啊, x 等于二啊, x 啊, y 等于二,对吧?那么这一等于 sf xy, 那我们跟这里稍微不同,不同没有关系,这里面只是告诉你下面啊, 如果 x 一知道的话,下面是把 x 一带你算,如果 x 二知道,下面把 x 二算,那么在这里调用函数,就是说你使用这个函数,只要这个 x 值在用之前知道他的值就可以。 x 之前我们知道已经复制给印了 y, 在这个进入函数之前啊,我们要知道这个值外等号,那么这个得到的结果算出来就是这里面的,算出来这个值 y 啊,输出量就是整个函数值,然后我们把整个函数值负值给这啊,所以呢符号不要。那么希望大家理解函数的本质意识, 本质意思就是说把 x 一 x 二作为已经知道量下面主体,把这个外算出来, 外算出来就是相当整个函数值,整个函数值,我复制了一个新的变量证啊,复制个新的变量证,这是相当有两个啊,有两个啊,输入啊,有一个输出, 我们也可以把两个输入合成一个输入,把它做一个项链放在一起,那么就产生了所谓的下面这种啊,我们 我们可以定义输出 ffo, 是吧?你用一个 x, 现在一开始虽然是一个 x, 但是我已经规定 x 就是一个项链有两个分量的项量,那么既然规定有两个分量项量,我下面要删除这个 y 呢? y, 那么就 x 的第一个分量, 第一个分量的平方加上 s 的第二个分量的平方,那么这样我们也就定义好了 f f, 好,我们保存,那么现在函数名称是 f f 二 啊,我们要调用的时候,那么这个时候使用 ffo, 如果我们这样调用的话,那这个就会出错了, 说错了,不信我们试试看。我们点运行,他告诉你这个输入参数太多,因为你这里逗号中间,那么就相当输入了两个参数,而函数第一里面只有一个 x, 所以你正确的用法就是把这两个做一个整体,用个中号表示啊,定义成一个起正中国号,那么也就是这整个就是一个,现在是一个整体附近去,他有两个分量好,我们就可以运行他,这就相当于 虽然是多元函数,但是可以作为项链函数啊,项链函数,那如果我们要定义这样一个函数呢?有两个输入,两个输出, 我们要定义啊, y 一等于 x 一平方,加上 x 二平方, y 二等于 x 一平方减 x 二平方,那我们再写函数就有四种方式来写,他 就四种方式来写字,第一种方式我们就啊,我们来说这样函数第一种方式就是说 我可以说 f u n c t i 啊,第一函数我的输出啊,是两个 y, 一百二啊,一百二,这样写,再把中间用逗号分开,那么等 一,我现在是 f f 啊,三个 f 吧,一,那么这个输入啊,我用两个 x 一 x 二,那下面就通过 x 一 x 二算出八一 y 二来输出。里面啊, 是用这样表示有两个输出啊,两个输出,那么 y 一呢,等于 x 一的平方啊,加上 x 二的平方,你可以加个点啊分号,那么 y 二呀,算是 y 二了,等于 x 一的平方减 x 二的平方, 那么这样我们就定义好了,这就相当于把它周围两个字变量啊,两个应变量,两个输入,两个输出。好,我们可以按照前面的方法把两个输入整合成一个,那么得得到第二种定义方式,那么也是 y 一 y 二等于 f f 二吧,那么 x, 对吧,那下面写,你就算出 y 一 y 一,怎么算呢? x 第一个分量的平方,加上 x 第二个分量的平方啊,那接下来是,嗯, y 二等于 x 第一个分量的平方, 减掉 x 第二个分量的平方啊,证明是好了,我们也可以把整个输出啊合在一起,作为一个矩阵来输出,那么就可以所谓的这样来定义三个线啊, 啊,下面啊,我们接着接着写到下面来,那么可以 y 等于 f f f 三啊,可以使用 x 一 xo, 那么要注意,现在两个输出都合在这里合成一个项链了,那我们就应该这样写, y 的第一个分量, 那么可以等于 x 一的平方啊, x 一点的平方加 x o 点的平方啊,分套啊, y o 等于 x 一点的平方,减 x o 点的平方。 那么第四种方式就是说我们把输入输出啊,都合成 一个 y 等于 f f 是 x 啊,那么这个是 s, 就有两个分量, y 有两个分量, y 一 y 二,我们分别把它算出来, s 有第一个分量啊,加上 x 第二个分量啊, s 一的第一个分量的平方减 s 第二个分量的平方,这就是所谓的多元函数的第一啊,多元函数第一,那么在调用的时候,如果你一定要调用这个,那你就必须啊这样 来调用,那么比如说我们要得到 ab 对吧? f f f 一二三这样调用,那么对这个呢,调用呢,就是让他把这个二三呢,用一个中国号括起来,那么这里调用就是 ab 等于 f f f 二二三啊,那么这里调用,那怎么调用呢?那么这里只能写个啊,写一个合在一起啊,写一个 c 啊,等于 f f f 三对吧,那这里二三对吧,这里写个 d 啊,等于,嗯, f f 四啊,二三好起来,那么我们要得到这个 c, 那么 c 有两个分量,那么你可以用 c 一取得第一个分量, c 二取第二个分量,第一第二选好啊,我们 来演示一下啊,第四个函数调用和调用,以及啊,第一啊,那么第四个函数呢?是这样第一的啊, 那么 y 等于 f f 四啊,输入使用一个 x 啊,我们要删除外的第一个分量来,那么点 x 第一个分量的平方,加上 x 第二个分量的平方啊, y 二 等于 s 第一个平方啊,减掉 s 第二个分量的平方啊,那么这样一下就有两个速度输出了啊,我们保存 作为这个函数,那么调用呢?我们在命令仓的可以直接调用,比如说啊, a 点一, f f 四是吧,二三,注意这里参数他值一个,但是是一个项链, 在我们这 a 就有两个分量了,十三和负五,那么 a 一不就得到十三, a 二就等于负五,这就是我们所要的函数的定义。好, 那么既然函数的定义和数学上的习惯是一样的,但是迈开步里面函数的定义稍微更广泛一点,这里输入输出啊,不一定是数,也可以其他的一些啊,数据类型,甚至是字幅串呢,函数名称呢,函数函数的地址啊等等都可以, 那么无非他属于我们统称为参数啊,就不再叫做自变量啊,自变量,那么对于参数的意义来说,对于参数的意义是,如果我有啊,任意多个,我在我在你调用之前,我不知道你会输入多少个参数,那么怎么来处理 任意多个参数的意思呢?那我们就使用这个命令啊,使用这个命令来处理任意多个参数为 a r 啊,这是变量的意思,变化的意思啊, a r g 表示参数的意思, argument, 那么 i n 是输入的啊,参数是可变的啊,或者我们使用 var arg out, 这是 out 输出, art put in put argument 啊,那么这是表示第一啊,任意多个输入会输出参数与任意个参数, 一个是用的输出,一个用的输入,那么我怎 我们来判断你得到多少个呀,我们 number 啊, n, 参数个数 a r g 啊,输入的参数个数 n, 那么以及 n, a r g alt, 那么这是输入参数课程,那么我们就要得到啊,实际输入参数的个数, 实际输入啊,或者输出啊, 唱一首歌送, 这样我们就可以来定义啊,很多个参数的意思,我们来举个例子啊,说明这个意思,现在就说,我来定义,你输入两个数,我就把两个数加起来,你输入三个数,我就把三个数加起来,那我们就这样定义 啊,我输出是一个纸盒,那么我,我要上啊,啊,我, 我两个 ssrum, 我输入参数,我是任意多个都可以, vir argument 啊,输入参数个数,那我们想得到,你到底是几个参数呢,对吧?这得到几个参数啊,那么 我们就想知道啊,你这参参数个数啊,这参数个数,那么我外啊,我就等于你所有的参,输入参数之和啊,输入参数之和,那么参数是放在这里面,对吧?那就啊, a r v a r a r g i n, 这是第一个参数啊,加上啊, 如果有两个参数,我们就加上第二个参数,那么如果有输入哈,有很多参数,我们就不如把它加起来, 这样我们就可以输入很多的参数了,那么我们等我们讲完循环,我们再来讲这个参数,我们法律输出一个简单哦,也就是这个时候啊,不管输入多个参数,我都可以运行,但是,呃,我,我都是 y, 等于哦,通过输入我算的输出来 啊,我们要把所有的参数都加起来,是吧?呃,这个方法我们后面再实现,现在我们就可以在这里调用 y 等于 ssum, 对吧?我选一二,对吧?输入两个参数也可以,我输入三个参数也可以啊,输入三个参数可以,甚至我们来来显示下,我知道你输入几个参数, disp, 我们输入说,我,我显示参数个数啊,我,我就显示你啊,参数个数, n, a, r, g, argia, 这是我显示你参数的个数。是这么多,那么这个时候我们来 啊,这里保存啊,保存,那我们看看, y 等于 s, s u m 啊,我一二看看是不是得到两个参数啊,得到两个参数啊,我们就直接把 y 复制给 n 啊,加 n 啊,就是把参数个数复制给 y 嘛,复制给 y, 那么我们看 y, 如果我输入三个参数呢,我就得到三个参数, y 就等于三了,显示,显示了三,就是显示命令可以把它删掉。 好,那如果我输了五个参数呢?一二三四五。好, 那么这个就是说我可以任意一个参输入,呃,输入参数,我可以用这个取得参数个数,我也可以任意输出个参数,我也可以取得输出个,所以我们可以看到内部命令往往会有多种用用法,如果你是两个参数,我怎么办?如果有三个参数怎么办? 我们举一个简单例子,如果你这个参数是两个啊,那么我们假设你参数个数用 n 表示啊,啊,如果啊, n 等于啊,如果只有一个参数, 那么我就什么呢?我就输出外来外,就等于啊,第一个参数值。好, 如果啊,我按是等于二两个参数,我 y 就等于两个参数之和,第一个参数加上 第二个参数。使用这个方法做一个参数,那么在它里面所有的参数啊,其实就是逗号分割的一个单元体,使用这个大括号取出他第一个单元里面就是第一个参数值啊,如果是两个参数,那我们就输出两个参数啊,结束, 结束。好,这样呢,我们就写好了这个代码,现在我们来看看,现在是如果是两个参数就等于三,是吧?如果是一个参数呢?嗯, 我就等于啊,他本身,对吧?等于他就第一个参数值啊,如果是两个参数,我们就把两个参数加起来,对吧?好,我们也可以说我们也是多个输出参数啊,我们可以变任意多个 啊,输出参数啊,任意多个输出,那么在这里如果输入是一个,那么我输出啊,啊,我的输出啊, 我,我第一个输出参数,那么我就是等于你输入参数,那么如果说 如果我有两个输入输入参数,那么我输出参数也来两个,第一个 是两个之和,第二是两个之差啊,第二个等于两个之差, 好,呃,保存,对吧?现在我们来看一看哈。如果输入是一个参数, 输入输出也是一个参数,那么 y 等一啊,二十 sum 二,那么 y 就等于二,那么如果输出是两个参数, j y 和这,那么输入啊,是啊, ssum 二和三, 那我们就知道第一个啊,直至外就他们两个之和,第二就他们之差,这就是所谓的可以控制任意多个输入输出参数也可以控啊,或者输出输入参数个数个数,那么特别的,如果我一个 没有输入分没有输出啊,这是可以的啊,那么就是说无输入参数啊,啊,无输出啊, 那么这要分几种情况,第一种情况就是有输入无输出。第二种,是啊,第一个是无输入,无输出啊,无输入,有输出啊,有输出。还可以啊, 有输入无输出啊, 那么有收入,对吧? 有输出,那我们前面就看到有输入输出,还有多少个的问题,那么像这个都比较简单,我们举个例子说, 你能说我这样写 functiv, 是吧?那么这个时候我不要写着 ff f 啊,五吧,那这样就是只有函数名称,没有输入,也没有输出,输入放在括号里面,那我们在地面,比如说我显示 啊,一个制服 a 啊,一个制服 a, 那这个函数就做这样的事情啊,或者说我我直接写行 y 点二啊,写个啊啊,写个 a 点二啊,定一个 a a 点二,好,那么定,如说我定义这样一个函数, 我没有输入,但是有输出的 ff f 六吧,啊,没有输入输出,我就是通过,不需要什么我把这个 y 给算出来啊,就要把这个函数未知的东西算出来点,哦, 就可以了。你甚至可以说,呃,我啊有输入啊,但是不要输出 f f f 七八,我只要一个 s, 告诉我 s 啊,我把 s 的 平方显示出来,就可以 s 平方打印出来,加给他打印出来,那么这些都可以看到,看到,哎,世上 那么这些啊,呃,这样一些无输入无输出的里面有一个特殊情况,就是说 当我这个没有输入的时候啊,你是可以点运行的时候,直接算他的结果啊,那么这个时候我们可以看到像我们前面这些函数都是有输入有输出,你点运行的话啊,那这个就不好办了,是吧?你想这个啊, 有输入有输出的话,你点运行,他就会提示你错了啊,听错了,像刚才这个是任意多个都可以,零个也可以,那么如果一个行业是无输入也无输出呢?那我们就好办啊,比如说,嗯, 我这个没有输入也没有输出啊,我就是显示,嗯,还有啊,好,那我们就做这个事情保存,对吧?那我们 就可以点运行了啊,这个函数啊,功能就是做啊,显示是哈喽,这样一个啊,单词,那么如果有输入话,那你就不行了,所以说你就要 提供输入,这是函数关于有输入和无输出的情况,那么有的时候我们就会出现你输入了两个参数啊,输入需要两个参数,结果你只输入一个参数,这就会出错了。 但是对输出的情况他不是一样的,如果你要求输出有两个参数,结果你只用了一个参数,我们来试一下啊,这样一个情况,好,我们啊,假设我们第一个函数啊,第一个函数 我有两个输出, y 和 z 啊,等于 f f 七啊, x, 嗯, y 对吧? x 六和 v 吧。啊, 我外呢?是哈,我要通过右位算出这个外和这来外,是的,右加上位, 我这样等于右减七位啊,右减位,那么这个函数就是有两个输入,有两个输出。好,我们来试一下,比如说我只提供一个输入, a 等于 f f 七啊,三个 f, 四个 f 七,我二和三,是吧,那我们就就算出了啊,一个五五就是他的第一个参数值,这是没有提供第二个输出参数。如果我们提供了第二个输出参数, a 和 b 等于 f f f 七 二和三,那我们可以看到这样就输出了两个,一个是 a, 等于两个字和 b 是,那这个时候我们就不能理解为负 负值了,这个时候我们就要理解函数调用,函数调用,那么在这个时候呢,我们也知道不能理解为负值,你可以理解函数调用,函数调用就说 把默认的啊,如果说后面的参数缺少了,那么后面参数啊啊,这些计算量就不给你付出啊,付出复制过去,只把这个外给你啊,算的第一个,也就说默认呢,只考虑第一个参数,就是在函数调用的时候,输出参数可以省略 啊,输出参数可以省略, 可以省电,甚至一个参数都不需要的情况,比如说我们 这里有两个输入,两个输出我,我没有,我输出一个都不提供,我直接 f, f 啊,七是吧,三和四是吧,那么这个时候他就是把这个第一个参数值作为默认的输出来啊,默认的输出来, 那么这就相当于他啊,可以省略的,或者哈可以补全啊。像我们说怎么补全一些参数呢?那我们可以使用前面那个技巧来补全一些参数, 那么如果我们要实现自动补全参数,那只有自己来实现啊,补全参数,呃,我们举一个例子来说啊,是这样处理补全参数的问题。呃,我们直接写一个代码啊,给大家演示下什么叫补全参数。嗯,新建一个 函数是 f u, n, c, t, i, 那么输出是 y 和 z 啊,输入啊是 f f, f 啊,是 f 六吧啊,不能重名 a 和 b, 那么这里要求是两个, 那么如果我想输入一个他也行的话,那我们就使用 narg, 哎,输入参数如果是只等一个,那么也可以啊,也可以,那我就自动把 b 补全为零,对吧?啊?结束,对吧?如果说输入参数 啊,等没有输入参数,我们也可以,我就把 a 补成零啊, b 补成零,这就所谓的一般来说默认值的问题 啊,就是我怎么设?如果有参数怎么办?那么这个时候我们就可以外就等 a 加上 b 啊,这我就可以等于 a 减去 b 啊, a 减去 b, 那么那么输出参数 我们也可以,如果你输出参数啊,如果输出参数你只得只有一个啊,只有一个,那这个时候我们说我就把 y 就改成 a 加上 b, a 减去 b, 就把这个整个的计算结果做一个项链把你输出来。好, 那么我们来看看这个什么意思?就是上面如果你只输入了一个参数,我们先保存, 那么我就默认币就是零,如果你两个都没有输入,我默认就是啊,都市零,都市零, 那么都市里如果你默认是两个数字参数,我就一个是两个字和一个字啊,如果你只给了一个参数,那我就是直接用销量说出来,那这个时候我们来测试它啊,测试它,首先比如说我正常的外和,这 就等于 f f f 六,对吧?我输了两个参数二和三,我们可以看到 y 就等于两个字和这等之一,对吧?那么现在呢?我们把这个删给删掉去 啊,那我们发现也可以,甚至歪和这外是两个字和这是两个字差,好,那如果说我哦也删掉去,一个常识都没有,我甚至这个胯也可以删掉去,那么这个时候我们发现都可以等于零也是对的。 好,现在我们假设后面是正常的,那但是前面呢,我们这里可以删掉一个,我们现在只有一个输出参数,一个输出参数 y, 那么这个是 y 就变成了项链啊,项链,项链。好,我们前面说 在任意多个参数我都可以处理啊,任意多个参数都可以处理。 好,下面我们来介绍这个啊,所谓的匿名函数啊,匿名函数, 匿名函数啊,虽然就是我有时候也叫做聚丙函数,这个词不太好理解,那么大家就可以看着所谓的匿名函数就是指的啊,我们 不需要函数的名称,函数只是放在这个啊,像这有五个抽屉,我并没有这个给这个抽屉叫做啊,这个衣服抽屉,鞋子抽屉,袜子抽屉,我没有,我就说这是这个抽屉,我只要知道地址就可以了, 所谓的记柄啊,分匿名函数都是一般是指的地址的意思啊,你可以理解为啊地址,那什么叫匿名函数呢?就是说 说,我这个函数没有名字了,没有名字我只有变量质,变量名字,我用个艾特符号代替他,然后我们下面函数的主体啊,是 x 平方加上二乘以 x 加上三,那么这样一个函数 把,这个函数我还可以复制给一个啊, f 复制给一个 f, 那么这个是 f, 就相当于函数名称了啊, f 就相当起的这个函数的地址 啊,那么我们把三放到这个地址里面,就放到这个函数里面去算,那我们就可以知道这个结果。好,我们来演示一下啊,那么事上,因为我们刚开始已经定义了这个函数 f 啊,已经定义函数 f, 那么我们把这个 f 删掉去啊,如果不删的话,那么你这样写 f 三,他不知道是使用哪一个 好,我们也可以测试一下他到底使用了哪一个啊,新建一个文件,是吧?那我们可以说我 f 等于 at 啊,这是匿名函数,我 x 平方啊,加上 x 平方,加上 ox, 加上三,对吧?那么接下来 fo 加上 fo, 我们运行他, 那我们看看他到底是调用了内部函数还是这个函数,那我们这是调用了这个函数啊,这就相当于 在这个地面并不需要二,但是这个里面我们也可以把这段复制给记啊,这个记,那么用记二表示,那我们就可以看到。呃,算出来记二也是十一啊,十一,那么在这里面我们可以看到这里有个函数,另一面函数 fg 啊,你可以把这个清掉去,没有关系 啊,这所谓的匿名函数。好,我们也可以这样使用,那内部函数是有一个啊, 上瘾函数,我们可以用 f, 等于艾特上瘾,我们取得上瘾函数的地址,接下来啊,我们输入 f 派, 那我们就实验是算出了什么上瘾派,对不对?算是上瘾派,用原来 f 是这个函数,我们运行这些,我们可能 f 已经改成了正确函数上映派。一,一点二二亿的服务十六次方,那么就接近您了,这就是正确函数啊, 这就取得函数的地址,嗯,取得函数地址,取得函数的地址啊,啊,我们知道我们在这里面已经有了 f f, 对吧?有,有这样函数,那我就可以使用艾特这个符号取得他的地址。 ff, 我们的两个 f 啊, f f 两个 f, 我们就取得他地址,那接下来我就使用 f 二三啊,我们来算这个啊, 就相当于算出啊 f f 二三,那么就是等一,这是啊,两个平方加起来,这就所谓的啊匿名函数,那么这个啊匿名函数呢?或者函数记柄呢?特别有用,比如说我们想对函数进行操作 啊,什么意思?什么意思叫做对函数操作呢?比如说你输入一个函数,那我就求出这个函数根,输入另外一个函数,我求出另外一个函数的根,是吧?求这根,那么这个时候你输入的函数是变化,我是要对函数进行处理,那 我们下面再求解这个根,对吧?求解根,那么我们这里就要使用一个函数放在这里啊,别墅呢? f, 对吧?我们要使用函数在零点附近的根,那下面就要使用 fx, 那这个时候我们就把函数的记啊地址传进来就可以了啊,传进来就可以了, 这就所谓的啊函数的地址和啊记柄函数,那么匿名函数是一个特别有用的啊,希望大家能够掌握,下面我们介绍指函数,指函数, 指函数就是一个文件里面有多个函数,比如说我,我上面有个翻跟线,对吧?翻跟线,我下面在同一个文件里面,我们下面还有个翻跟线,还有更多个翻跟线, 那么像这种函数,那么上面这一部分函数就叫的主函数,下面都叫的指函数,那么比如说这个是 f f f 啊八,那么这是主函数的函数名称,那你的文件名呢?就要和他是一样的 啊,如果主函数也可能有输入,也可能有输出,那么下面是指函数,那么只有主函数可以使用这个指函数,那么在外面呢,你只能使用主啊,在其他的文件里面,你只能使用主函数, 这指函数只能被他的主函数使用,这就是为了主函数和指函数的意思, 那么前面使用的匿名函数就特别有用,如果说我要在啊,在这个主函数里面 使用指函数,一般有两种方法,一种就是使用刚才这这种方法,一种是直接写函数名称的方法,都可以,你也可以有多个指函数,所谓多个指函数是指的这个意思啊。 f, 嗯啊,这是主函数啊, 啊,这是主函数,然后接下来啊,又是指函数啊啊啊,指函数,那么这样的话,一个组多个啊,多个指函数构成一个文件,构成一个文文件啊, 那么这些紫函数是相互独立的,相互独立的,那么紫函数可以互相调用。 呃,这是关于主函数和指函数,那么下面一个命令是 叫做千套函数啊,千套函数啊,就是说我最外面有一个函数,函数底面还有一个函数啊, y 表示 fx 啊,那么这个函数底面还有个函数 啊,还有一个函数啊, b 等于 f f, a 啊,但是我们这样写话,上面就变成主函数,这都在一个文件里面啊,一个文件里面上面都变成了啊,主函数,那这个时候我们要加按的啊, 这按的就表示这是最外面的,那么这里要加个按的,那么中间是函数的主体,函数的主体啊,这下面可能还含有其他的代码,这都是主函数的代码,那么这一部分呢,就是指啊,被欠套的函数,被欠套, 那么这就带按的,那么这种函数啊,一般我们用的极少,但是这个函数有个优点,有个优点就是说这里面的变量啊,如果在这个不是他的参数啊,那么这个变量在这里面是相同的变量啊,这可以共享变量, 共享变量,或者说你主这个啊,外最外,最外的这个函数,他其实是全集变量啊,全集变量, 比如说我这里面可以写 y 的 x 平方,那就是 m, x 是这个这个变量,那么在这里面你也可以直接使用 x, 那如果这里有 x, 那重复了,那么这个时候他就这个 这个被签到函数的,就会暂时把外面的盖住啊,出来又会恢复啊,所以说在这个签到 大人水里面一般很少使用,因为这个变量比较混乱啊,有的是全集,有的是非全集。好, 那么调用规则是这样的啊,调用规则是这样的,你这个外面的可以调内内部的,内部的不能互相调用啊, 那么在模特步里面还有其他的函数啊,第一个就是说使用的啊,依赖函数,那么现在已经废弃了啊,已经废弃了,不能用了啊,不能用了,我们也就不用介绍了啊。还有一个是使用符号 啊,符号函数啊,符号函数,那么就是说我们有符号变量啊,符号变量,那么这样一个问题,就是说函数互相重名的问题啊,重名啊,我定义了一个正确函数, 内部有电影函,内部函数,那到底啊,呃,以哪个为准呢?那么优先规则就是说啊,像我们刚才用的,你有匿名函数,又有这个函数,又那个函数到底是使用的 啊?我觉得这个没有必要介绍,一般来说是你自己定义的函数优先,然后说啊,目录下的函数哈,匿名函数优先,再是你目录下函数,再是内部函数,那么像这个就很混乱了,所以我们建议大家不要出现重名的啊,不要重名的啊,重名的函数 就是说一定要区分所有的函数名称来,函数名称来,那么关于函数,我们大概就是这些内容啊,今天讲到这里,谢谢大家。
298xuzhijun 06:52查看AI文稿AI文稿
06:52查看AI文稿AI文稿今天我们一起来学习算数运算函数,除了可以利用算符进行算数运算,曼特拉伯还为求和、插分、求机等运算定义了专门的函数。 常用的算数运算函数,比如说求和,利用 sum 插分对付求积、 proud 平方跟 s q r t 等等。我们首先一起来看一下求和, 求和的函数是萨姆,基本语法是这样的,我们通过具体的实力一起来看一下。首先在命令行输入一个魔方矩阵 a, 输入命令 a 等于 magic 三,也就是定义一个三行三列的魔方矩阵。 所谓的魔方矩阵指的是行列对角线元素之和相等。 我们现在对魔方矩阵进行求和,输入命令萨姆 a, 当没有指定纬度的时候,他就是按列求和,当我们输入参数二的时候,他就是按行求和。 比如说在面临行输入 som a 二,这个时候就是按航求和, 返回的是各行元素的和。萨姆函数也可以对多维数组求和,比如说现在我们将 a 矩阵扩展为三维的一个数组,在命令行输入 a 圆括号里 冒号逗号,冒号逗号二,等于 a, 这个数就变成了一个两页的一个三维的数组。我们现在求按页求和,那就是输命令 some a, 逗号中括号里一二,这个时候输出 结果是有两个,这个是第一页的元素之和,这个是第二页的元素之和。 当我们指定奥参数的时候,他返回的就是数组中所有元素的和。比如咱面临行输入 some a, 你看现在报错了,对吧?原因是因为我现在是用的是中文字体,应该切换成英文字体 sum a 单引号里面输入,哦,输入这条命令返回的就是数组中所有元素的和,只有一个结果,这是 求和。我们再来看一下插分,插分的基本语法是这样的,我们还是通过具体的实力一起来看一下。首先定义一个数组 x, x 等于 e 尾的一个数组,元素是一二四七十一,我们现在对这个 e 尾的数组进行插分,输入命令 y 等于 d, i, f, f, d, x, 结果变成了四个数,他是相邻元素的差分。如果 求 n 界查分,相当于对付函数迭代了 n 次。例如我们在命令行输入 dif f 对付 x 逗号二, 他就是在刚才 y 的基础上再迭代一次,这个时候元素只有三个了, 这个命令相当于在命令行直接输入对付原括号里对付 x, 这个结果跟刚才这个结果是一样的,所以注意了,每求一次插分,返回的项链的长度就减少一, 那如果是 p 乘以 m 矩阵,这个时候差分返回的大小为 p 减一乘以 m 的矩阵,元素就是 x 的行之间的差分。 我们来看个实力令, x 等于第一行一三五,第二行七十一,十三,第三行十七十九,二十三。 这样一个三行三列的矩阵,我们现在对他进行插分。另 y 等于 d, i, f, f, x, 会发现结果变成了两行,因为他是这个时候是求行和行之间的差分, 那如果要求按列元素插分的话,就需要指定 n 和参数。命令行输入 y 等于 d, i, f, f, 原括号里 x 一二,这个时候的结果就是按列进行插分。 对于对付函数,也可以用于多为数组,每求一次插分,返回的数组在插分进行的纬度上的长度就比原数组减少一 好,这就是算数运算函数中的求和和差分。关注我,明天咱们再来看其他的运算函数。
62朝霞szx 07:00查看AI文稿AI文稿
07:00查看AI文稿AI文稿今天我们继续学习 maclub 算数运算函数,在上一个视频里,我们一起来学习了求和和差分,今天继续学习其他的运算函数。首先来看求积 囚机的函数是 prod, 他的与法格式与前面介绍的萨姆函数完全一致。我们还是首先来看一个实力,在命令行产生一个魔方矩阵 m a g i c magic 三,产生一个三行三列的魔方矩阵 a。 我们现在对矩阵 a 进行求机,输入命令 b 等于 p r o d proud a。 当没有输入参数的时候,默认是按列进行求机。比如说九十六第一个元素就是第一列的 八、三、四这三个元素球机,四十五是第二列一五九这三个元素球机, 八十四是第三列的球机。那如果想求按行进行球机的话,就要加上参数二,输入命令 b 等于 proud, 原括号里 a 二, 这个时候就是按行径求机。同样如果加上奥,这个参数 b 等于 proud, 原括号里 a, 奥放在单引号里面,这个时候只产生一个元素,他是 a 这个矩阵当中所有元素的成绩, 这是对于函数求机 prod。 下面再来看平方根,平方根对应的函数是 sqrt, 他返回的就是要求的数组中每个元素的平方根。 比如我们在命令行输入命令 y 等于 s, q, r t, 负二到二,输出结果就是从负二到二这五个元素当中每个元素的平方根。 好,这是求平方跟 sq r t 函数。下面再来看一下取整。曼特拉布提供了四种取整方式, 我们首先在命令行创建一个随机数据阵 a, 通过实力一起来看一下具体的取整方式。在命令行输入 rng 零,再数五命令 a 等于十点乘 二 and 四在十五命令 a。 这条命令是让最后一行变成一个复数。好,这样就产生了一个随机数矩阵 a。 下面咱们对矩阵 a 的每一列用不同的取证方式,注意观察他们的区别。对 a 的第一列输入命令 二,运用四要函数向上取整。对于 a 的第二列, 用 fix 函数向零取正。对于 a 的第三列, 运用 flow 函数向下取整。 对于 a 的第四列,运用 round 函数四舍五入 至输出结果。第一列向上取整,结果为不小于当前数值的下一个整数。 第二列向零取整,所有的小数部分被截去。第三列向下取整,结果为不大于当前指的下一个整数。第四列为四舍五入。好,这就是取整。 再来看取于迈特拉布中有两个函数可以计算余数,用帽的函数 称为取魔运算 ram 函数称为求于。运算猫的函数等于 a 减 m 点成 flow, e 除以 m。 ram 函数等向于 a 减 m 点成 fix, a 除以 m。 通过视力来看他们的区别。我们在命令行输入 a 等于 负三到三,产生一个一尾的一个数组 输入命令 mode m o d, 这是结果好,再来看一下求于的函数, ram 命令行输入 方括号 r e m rem 会发现两个结果是不一样的,帽的函数与除数的结果同号,而 ram 函数与被除数的结果同号,数值也是不一样的。 好,当除数为零的时候,冒的返回被除数,而 rem 返回无穷大。比如我们在面临行输入方括号 m o d a 零 rem 一零来看结果,第一行是帽子的输出结果,第二行是 ram 的输出结果。 好,这就是 matlab 算数运算函数中的求机平方根取整和取于。 那今天的分享就到这里,关注我,后面咱们再来一起学习迈特拉伯的其他知识。
104朝霞szx 08:41查看AI文稿AI文稿
08:41查看AI文稿AI文稿今天主要介绍一下 matlab 的 for mini 四的函数去求解多元函数的一个最小值。 嗯,在求解这个无约数多变量函数的最小值的时候,我们可以使用否米尼斯的全数啊,他的功能的话就可以使用无导数法去计算无约数多变量函数的最小值。呃用的比较多的,比如说我们如果是只要求在哪个点取的最小值的话,我们就是输出为 一个 x, 然后在这个函数 form 社区里面的第一个输入的话,这个饭就是目标函数,然后这里的目标函数的话,就是我们要求的呃 最小值的时候 x 是多少?里面的 x 的话可以是一个变量或者是多个变量,他可以是向量形式或者是矩阵的形式,然后如果是有,呃第二个输入的话就是 s 零就是他的一个初始点, 然后这个 up 选的话,我们可以对这个求解器去设置他的一些参数,比如说他的一个迭代的次数的一个过程,以及呃最大的迭代次数,以及呃绘制的图形就是他的求解过程的动态图形 啊。同时的话,如果我们是用结构体来进行一个设置他的目标函数初始点,还有就是他相应的一些啊属性的话也是可以的。 然后如果我们要去求解他对应的一个啊最小值和最小值点,就是 s 是最小值点,这个是最小值,然后就是两个输输出 啊,或者是三个输出,这里面会包含了一些呃他的一个求解的一个属性,是求解的最优解还是近视解,然后以及呃如果是有四个输出的话,这个第四个输出 的话就是会包含一些优化过程的信息,主要是以几个实力来讲解一下。比如说这里面的一个,呃目标函数的话,他是 呃还有平方向的,这种就是非线性的。然后里面的话啊,二十的话有两个变量,一个是二十一,一个是二十二,然后他这个对应的函数关系是是一百乘以二十二减二十一的平方,再括号的平方加上一减二十一的平方,然后这是对应的程序,我们可以看一下。 呃,这个 c l c 是清除这个命令行窗口的一个历史的一个命令,然后 cleo 的话是清除工作区的一些以前程序生成的一些变量。 cleo 之后的话是关闭一些图形窗口,然后我们这里的话就可以通过这个 o p t i 呃, optimi set, 然后可以设置。然后, 嗯,这里的话就相当于我们这里使用的是三个输入啊,四个输出的,就所有的输出都包括了啊。首先的话我们先看这个目标函数是通过匿名函数的形式, i 括号 x, 然后这里的 x 的话就可以定义为一个变量, 然后里面的话有两个变量,分别我们用 s 小括号一表示 s 一, s 小括二表示 s 二,然后一百乘以二十二减二十一的平方,括号的平方加上一减 s 一括号的平方, 然后这就是目标函数初次点的话我们随意取啊, s 零的话,因为两个的话用动画间隔或者是空格间隔,那这里的话就是负一点一二啊。然后设置属性的话,我们就可以设置绘图的属性, 嗯,然后去进行一个设置,呃,设置它的一个函数值,然后这个 display 显示它的叠带次数和最大的叠带值。 嗯,这里面的话,那就是进行一个设置,这里就是目标函数,这是出示点,这个是参数。我们设置运行之后的话,我们可以看到啊,看到这个啊,求解的一个过程啊,这个的话就是横坐标的话是迭代次数, 嗯啊,刚刚可能点一下子点了那个停止,然后我们重新,嗯,运行的时候 啊,这里的横坐标的话是迭代的一个次数,重坐标的话就是这个目标函数的值,我们可以看到这就是一个这个设置,他的一个绘图属性的一个这个,然后我们再可以看一下他这里的,嗯,会显示他的 叠带次数的一个叠带过程的,然后这里的话 s 的话取取 s 一 s 二取一的时候,对应的目标函数值是八点一七七乘以十的负十次方,那接近于零,然后这里的话返回为一,一的话就是表示比较好的,然后这里面的话就是会闪 设置这个 output 的这个,呃规划的一个路径, 然后这个是程序运行结果。然后第二个实例的话,我们可以看到这里面的这个 f i, 它就是一个 i 重复十到十的一个过程, 呃,这里面的话就是相当于一个一系列这样的函数进行一个累加,然后我们这里的一个主程序 的话就是,呃,在这里面就是相当于这个函数的话,呃,这个 i 的话会,呃重复执行二十次,相当于有二十次二十个这样的函数进行累加,求最小值,那这里面的话我们可以看一下这里的程序的话是在这里的, 因为它也是两个变量,虽然它有二十个这个函数相加,然后 s 零的话就是零零二五,负零零二五,然后这里的话可以通过这个 o、 p、 t 设的,所以设置它的一个绘图的过程。然后这里面的话我们可以通过目标函数,可以通过函数自定义的形式 啊,就是制定函数,这里面的话就一个 option, 然后这里面的 option 的话我们我们然后这里面的 f 的话等于零,然后这个负循环的话就是 k 等于负十到十,也就是他这个 k 的话每隔一取一个点,取一个点,然后直 行一次循环,然后这个循环的话 f 一开始等于零,然后 f 的话就相当于进行一个累加嘛,然后加的话就是这个 esp, 就是在后面这段就是这个函数部分,然后他会执行二十次,那这时候二十次循环之后的话,那这里的 f 的话就是在后面这个函数的二十个 雷加,然后作为这个输出复制的这个 f, 然后这时候的话我们的这个第一个输入参数,就是这个目标函数,可以通过这个 i 的去定义,然后这里的 x 零是这个,然后凹陷是这个,然后这里返回是 x、 c 和这个标志,我们可以看一下它这个过程 函坐标是这个迭代的次数,众坐标是函数值,那我们可以看一下这里面的 x 的话啊,二十一区负零点一六九六, s 二区负零点五零八六啊,最小值对应的这个, 然后这个是程序和运行的一个结果,然后是第三的话,我们可以看一下,也是一个比较简单函数,就是一百乘以 x 二减 s 一的平方,空号的平方加上 a 减去 s 一空号的平方,我们可以看到里面是关于 x 的,那就是 s 一 s 二是这个变量, a 是未知的参数,那这时候的话就是考虑到,呃,如果里面的话还有这个未知参量的时候,怎么去进行一个操作 啊?这个函数的话就是一个这样的,比如说我们的 f 的话是也是通过匿名函数的形式去进行一个定义,首先这个 x 的话 啊,艾特框 s, 这个 s 是变量,然后里面的 a 也是变量,那这时候的话我们就要呃把 a 当做一个参数,位置参数啊, s 的话是变量,然后进行一个嗯 匿名函数的定义,然后这里的 a 的话,我们假设这个 a 等于三嘛,然后这里的时候啊,如果是 a 是已知的,就是它是可以改嘛?然后这里的范的话,那就是 i 括号 s, 然后这里调用这个匿名函数的时候,要输入这个 x 以及这里面的这个 a 的话是已知的三, 然后这里的 x 零的话是负一和负一点九,然后同样是设置它的一个迭代过程的一个图像,然后这里是 find, 呃,也是通过匿名函数调的形式 x 零和这个 option, 然后我们进行一个运行的时候,我们也可以看到它的一个呃,迭代一个过程, 然后这里是 s 一 s 二的距值,以目标函数的值,这里是接近于零嘛,因为它是三点四四七二乘以四的负十一次方,然后这个 一个叠带的一个过程运行结果啊,今天主要是简单的以几个例子去讲解一下这个求解器,因为所有的求解器它实际上它的一个 啊语法也基本上差不多,主要是看你的一个实际的需求,然后,嗯,今天主要是介绍这个,谢谢大家。
14龙行天下 17:02查看AI文稿AI文稿
17:02查看AI文稿AI文稿公众号的二维码,然后这是公众号的名字,羽绒派程序和图文都在里面。 呃,今天主要是讲解一下玛莎拉贝的蜂蜜抗函数据,你和一些位置参数,就是呃, 他这个蜂蜜抗函数的话,前面也讲过是用于规划中,其实在求参的过程就是我们已知一个函数关系的输入 和输出,但是里面有一些呃未知参数是不知道的,那这时候去求解的时候,他实际上也是一个呃求求解规划的一个过程,所以的话也可以用这个蜂蜜的抗寒术去进行一个求解, 他的目标函数可以是他的一个你和参数,假设他是有个表达式,呃他里面的这个位置参数,我们作为这个 求解规划中的一个位置变量,呃,将这个椅呃椅子的这个数据,比如说椅子,假设是椅子一个 x, 就是它里面啊,你和函数里面的一个 x 和 y, 然后我们把这个目标值带进去之后,和已知的数据之间做差,他的取他的绝对值,那这样的累积值的话,就相当于有一组数据,他就有一个这样的一个你和函数减去已知的输出, 呃的一个累加绝对值的误差,绝对值的一个累加值,当这个累加值最小的时候,看,就是看这个参数什么时候去值的时候,这个目标还是说的误差值最小 啊。这里的话前面也讲过这个蜂蜜蜜咖这个函数啊,蜂蜜咖这个函数的话,比如说这里是目标函数,它里面会有 as 小于等于 b, 就是这种线性等式,不等式约束或者是非线性,这个 cx 是非线性函数啊, cs 小于等于零或者 ceq 等于零就是,呃,线性非线性的不等式等式约束条件,然后变量的话有一个上下 线,那我们经常用的是这种形式的,就是蜂蜜卡,然后这一个是密函数,第二个速度参数是它的一个变量的初始值,然后 abaqbq 分别是他的线性,呃, 不等式约束,线性等式约束的左边和右边的矩阵 lbub 是它的一个变量的下键和上键,这里老是非线性的一个条件,然后再是它可以设置一些参数, 那具体的使用的时候主要是一个实际的例子,呃,比如说我们这里是使使用了一个比较简单的非信息函数,假设 这是 y 等于 a 乘以三 x 加 b, 呃,我们要已知道他的一个 x 就是输输入的,还有就是 y 输出的,我们要求位置参数 a 和 b, 那这时候我们的话就可以去产生一个实际的一个输入输出去数据,因为我们先要获得这个实际的数据啊。这里的话就是以这个形式。这个 clc 的话是清除空命令行的窗口命令,这个肯定的话是清除工作区的一些变量,这个 clubs 手指握的话是关闭图形窗口。首先的话我们就是,嗯,在椅子就假设我们要求的这个 a 和 b 就是他的一个正符和他的一个,后面这个长数是二和一, s 的话是零到十,呃,每个一取一个点,就相当于有十一组数据,十一个十一 组数据输入,那这里歪的话就是 a 乘以三 x 加 b, 那这样的话运行之后这里会产生 xy, 它对应的分别是一乘以十一输入啊,一乘以十一的输出,那这时候我们就把这里的 x 和 y 作为一个输入和输出,那这时候我们就是反过来求,就是 求这里的 a 和 b 是多少,那这时候实际上也是一个规划问题,那这时候的话我们就可以去进行一个设置。呃,这里是获得输入,首先的话我们要去构建他的一个目标函数,因为在这个函数里面的话,呃,首先要获得的这个 参数的话,实际上就是一个范,第一个输入参数是一个范,范的话实际上是他的一个数,嗯,目标函数,目标函数的话,我这里是用这个范一一表示。首先要理解这里 输入的 x 我们要求的是什么?求的是这个系数 a 和这个 b, 所以的话这里的变量个数实际上是有两个,那你这这个 s 输入的话就是用一个,嗯,发群,就是自制定义函数的形式,定义的一个目标函数。 首先的话这个函数的名称是范一,这个名称和他这里的点按母文件的名名字要一致,那是范一。然后这个 x 输入 x 的话,我们的呃就为了方便几点,就是把这个 x 一,因为他只有两个边量吗?就 s 一 s 中的第一个边量叫啊,把它 叫 a, 然后就是复制为 a 啊,第二个变量复制为 b, 那这后面使用的时候,这个 ab 实际上就是啊一个位置参数,那这时候我们的目标函数是什么?就是我们把这个呃输入吗?因为我们这个目标函数是这个 方程是 y 等于 a 乘以三眼 x 加 b, 那这此数的 x 的话就是已知的,因为我已知的输入和输出,那相当于我,我就 把对应的输入 x 带进去,那这里通过这个运算, a 乘以三 x 加 b, 实际上会获得一个输出的值和已知的输出的值做差。也就是,呃,假设 啊,假设这里的椅子的数输入输出是歪,零就是我椅子,比如说 s 等于一的时候, 就是 s 零等于零的时候,他对应的歪零是等于一吗?那这时候的此刻的值就是一,那这里的歪的话就是相当于 a 乘以三引这个 x 的话,是取零的时候加 b 减去这个 y 零,那这时候对它取绝对值,那这时候相当于我的。呃,实际的一个参数就 是在这个边亮里面求的的一个歪,减去呃,已知的一个歪,那这相当于是两者之间的误差,误差的绝对值,然后把每一组数据的误差都累加起来,那我的目标来说就是让这个误差最小,那实际上就是相当于 我已知输入输出之后和他的一个呃,通过这个规划去求解,当 ab 取什么时候值的时候,呃,就是我的 你和数据和这个实际的数据,他们之间的误差最小,那这时候是相相当于就是一个这样的,首先的话我们就要把这个 s 零万零的数据带进去吗? 啊?这时候的话我们先不考虑,嗯,就比如说你实际的一个实验或者是数据会有偏差,那这里的话相当于啊,这里的 yy 是 y 零加上一个 l 乘以润润的 论的的话就是随机,随机数,随机数的话就是相当于我后面可能会考虑,呃,你这个实验数据和真实数据可能会有误差,就是理论值和你的测量值可能会有误差,这时候先不考虑就这个 l 等于零就相当于 y 等于 v 零吗?后面的话就不考虑, 那这时候的 f 的话就是这个目标函数的值,首先是零,因为他是有十一组数据,如果我写的话,比如说写的时候可能是 abs, 然后这个 yy 的话就是 a 乘以三眼 xx 是,呃, s 零吗?这里的面的 x 就是一致的 s 零 s 零的第一个啊, s 零空号一,然后一直在推,因为它是限量吗?限量的话实际上就是它的这个空号里面就是它的值可以缩影,然后 减去 y, 然后一,然后再加上嗯, a 乘以三眼 x 零括号二 加 b 减去 y 二,然后这样实际上可以写一大串,所以的话一中有一个循环代替 f 的话, f 等于零,然后就是一个字加,自己加,那最后这里的 f 的话,实际上就是哦十一组 数据的输入,呃,十一组数据的输入减去,呃,这个函数通过这个计算的时候获得的一个输入,他们两者之间误差的和取血的绝对是 这个,这个也应该好理解,那这样的话实际上他的目标函数就已经构建完成了,通过这个循环计算之后的话,这个 f 就是,呃,我十一组数据的输出,已知的,加上我通过这个函数去求解的这个 这个函数,这十一组的输出,他们两者之间对应的一个差值的绝对者之和最小的话,那这时候就是一个这样的,那这时候的话我们就是,呃,第一步是目标函数建好了,建好的时候有非信讯约束条件,这里的话是没有什么, 嗯,非先不等次约束,等次约束,所以的话这里就是一个空,这里的范二的话就是一个空距等于空矩阵啊, h 等于空局阵。然后第三个的话就是我们要去设置一些函数的参数, 你说我要吊用,吊用这个,嗯, 我要将用这个冯明妮卡。首先这是第一个目标函数的,就是目标函数吗?就是范一一,呃,可以 通过这样的形式内嵌的形式。第二个是不是参数是 s 零二十零的话我可以随机设吗?因为因为这里的纸可能是不是很好,就随机设,可以用这个随机随机数抡的二一, 这的话可以改成是呃伦的呃印, 也可以,或者是直接取一个小一点的数也可以,就是呃,因为他的起点不会影响太大啊,大概是这个范围,呃,因为大概参数的话就会是在那个范围吗?然后这里是呃不等式,就是呃 不等式先行约束, a 和 ba 和 b 和都是为没有的,没都是空的,空的话就是这里面的这个参数的话就没有 abaqbq, 就是没有现行约束,那这里对应的都是空值。然后这是 lbublbublb 的话, ub 就是一个上键和下键。我们假设的是这个 a 的范围是零到五, b 的范围是零到二,这是因为每个变量他大概会有个范围,如果没有的话就可以不写,或者是写一个服务,穷到正无穷。 然后这里是范二二,就是这个,嗯,非信心约束,他这时候去求减,这时候会求出一个 x 和 y, x 的话,他是会求出来两个,一个是 a, 一个是 b, 然后这里 y 的话就是他的目标函数值,目标函数值实际上就是这个误差值,累积误差值, 然后后面的话就进行一个绘图,就比如说我要把这个参数求出来了,我要嗯和和原始的数据进行一个比较,就是我求出来 a 和 b 有一个值,然后 我在求对应的 x 在这个范围内是什么值,因为这里面的 x 是零到十,每个一取一个点,我这里的话就 xx 是取的零,每个零点一取一个点, 这里的话就有个范三反三,那就相当于这里是制定函数,他有三个输入,分别是 xx 的话,就是他对应的一个输入 ab 就是对应的一个系数,那这样的话通过这个函数的话就可以求解。我这个参数求出来之后, 呃他对应的一个字,那这时候就进行一个绘图,会是原始的数据,然后你和之后的他的一个数据,我们来运行一下, 就可以看到球出来这个 x 二一,那这样理论值和实际值,因为是呃他这个数据是假设没有误差的,那这时候的话,他这里呃 求出的参数二一,和我们刚刚原始数据就是在采集的时候他的系数是一样的,那他这里的歪的话就是呃九点六一二五乘乘以十的负八次方,就是一个很小的数了,那基本上就是误差,就可以是看中是零,那这时候是效果比较好的。 然后我们还有另一种书写的方式,就是啊其他的函数是一样的嘛,我们可以去设置,通过这个结构体, 通过我们一看的话,我们可以去把对应的参数呃设置成一个结构体,然后结构体的话我们只要去调用这个结构体,我们就可以设置相对参数,首先的话就是这个设置他那个,哦哦,不听你,哦哦。选就是设置他的一个显示,可以显示他的每次的 携带次数和他的一个算法啊,这个的话可以通过这个 hope h ip hope 去查看他对应的一个参数,方便你看。啊 啊,这里面的话会有一些那种啊例子啊,我这里是按照他这里面的有一些这种例子,呃,就是有一些那种解释啊,他这里是也会显示这个输出,呃, 然后这里是通过这个普罗普罗普人点这个 op 选的话,这里的话就可以会生成一个结构体,呃,结构体的话就把它里面的 op 选设置成这个。 嗯,这里设置好的,然后求解器是用的是冯明康,然后这是目标函数,用的是范一 s 零的话是 零点五,零点五,这相当于是非现行条件的话是这个啊,范啊啊,那这时候去进行求解的话,他也会求出来,后面的话就是一样的。那我们运行一下的话, 呃,就可以看到这实际上他会把每一次迭代的求解的过程显示出来,然后这对应的一个值也是一样的,因为这里数据没有变嘛,他实际上就是改了一种形式,就是它里面的话会有一个 允许这个结构体进行对他这个参数函数进行一个操作,就是类似于面向对象的一个编程 啊。这时候的话我们还可以考虑一下,就是因为我们,因为我们刚刚的话是没有考虑这个误差的,就相当于啊,我的这里的啊使用的输入输出都是和 和他理论值是一样的,那这时候的话就可以加一点误差,这时候的话就可以在这里假设这个阿鲁的话取零点零零一,然后点击保存, 我把其他的关掉,然后我们用这个结构体的吧,因为他也是一样的,我们就点击运行的话看一下 啊,这时候的话他的误差就会比较大了啊,因为他的一个变化的一个趋势的话,可能他的一个数值,比如说他的一个弯啊会比较小,就比如说他里面的一个, 你们可以看一下它的一个值,可以看一下这里的呃,一些值的话会比较小,那所以的话一个小的误差可能会影响这个函数的一个求解的过程。有时候去 零点一在运行 零点五,那这时候的话我们就是要对这个初职有要求,要求会高一点,因为他会在初职附近去搜索,比如说这时候的话我们就是改牌的改正啊,一点一点二就改在那个范围, 呃,一点五吧,一点五,一点五,零点五。然后我们去看他的一个求解的一个过程, 这时候的话他就是对初职会比较敏感,就是有误差的时候,就是我们要大概的估计这个参数的一个范围去进行一个设置,比如说如果设到一点九,二点零一点, 那这时候的值的话,他就会,比如说我这里已经是接近一幕实际的这个参数值了,如果出值的话,他最后最后求解过来的话就会 比较相似啊,所以的话他这时候也如果是你的测量值和这个理论值差距太大了,因为函数组合的话有很多可能性,所以的话这时候的话就是 他那个求解出来的参数可能就是合理论值会有些误差,但这也是允许的。一个范围 的话,我们对参数进行一个估计的时候,我用可以用这个方法去尝试,然后看结果怎么样,可以和其他的方法做一个对比。然后今天的话主要是,呃,讲解这个蜂蜜咖的求解这个 未知的一个你和参数的一个过程,就是已知输入输出的时候,然后这里是对应的一个程序和这个结果啊,总体来说他的一个思想和这个程序会比较简单。 然后,哦,谢谢大家,今天主要是。
7龙行天下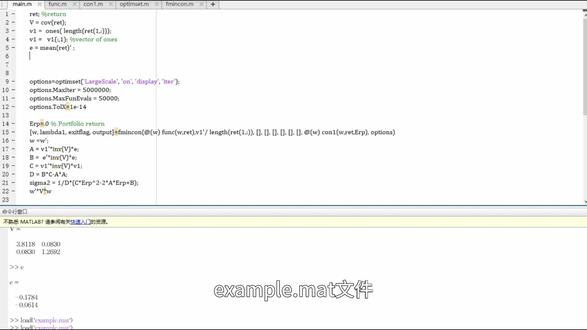 05:12查看AI文稿AI文稿
05:12查看AI文稿AI文稿example met 文件里面是二零二二年上证指数和标普五百的日度收益率。假设日收益率服从独立同分布,也就是说收益率是一个随机变量,其概率分布的期望和方差斜方差矩阵势未知的。 根据大数定律,可以采用样本的均值作为指数收益率的一致性估计。采用样本的斜方叉作为方叉斜方矩阵的一致性估计。 值得注意的是,我们关注的是每一个点的收益率的概率分布。一段时间的数据只是作为一致性估计的。样本 代码里面, b 复直 covariance written 及计算样本方叉斜方叉矩阵得到总体方叉斜方叉矩阵的一致性估计。 v 一复值 one's length written 一冒号 v 一复值 v 一冒号一,即得到向量一 e 复值 mean written 的转制,即计算样本均值得到总体期望一致性估计。 下面验证以下,当期望收益率为零时有效。前沿上方差的取值部分优化器的可选参数如下, maxitir 允许的最大迭代次数是正标量, maximus 允许的最大函数计算次数是正标量。 tox 中指容差是正标量。回顾上一讲,我们要求的问题是,在约束了期望收益率和权重的条件下的方差最小的组合可以用 f m i, n, c, o n 函数用来找到多个变量函数的约数最小值。语法为, f m i n c o n f u n x a b a e q b e q l b u b noncom options origin f u n 规划问题的函数 x 变量的初始值约束 a x 小于等于 b a e q x 等于 b e q l b 小于等于 x 小于等于 u b none con 非线性约束条件, 我们在此定义 f, u, n, x 和 noncom 就可以得到答案。另开一个文件,命名为 funk m。 然后定义函数,我们需要传 含入收益率的数据,计算方叉斜方叉矩阵率。定义变量 w 是指数的权重,是我们要求的结果。 d, e, f 复值为规划函数零点五 m a x w 的转至 v w, 这里默认求最大值,因此加符号。 另开一个文件,命名为 conyom。 然后定义约束,我们需要传入收益率的数据以及期望收益率。 计算均值意,以及定义项量一,没有不等式约束,因此定义 c 等于空有等式约束两个, 第一个是 c e, q, 一等于 w 的转制成 v 一减一。第二个是 c e, q, 二等于 w 的转制乘以减 e, r p。 我们首先检验期望收益率为零时组合的最小方差。定义变量 e, r, p 复值零。运用 f m, i, n, c, o, n。 这里面艾特 double 六的含义是, w 是需要求得的变量,其他是传入的参数。 得到结果以后取 w 复值。 w 的转制,按照上个视频的公式计算 a, b, c, d, i n v 是球逆进而根据 sigma 的平方的公式计算 sigma 的平方, 得到 sigma 的平方等于三点八六七四,然后将求得的权重带入方叉斜方叉矩阵的计算公式, w 的转制成 v 乘 w, 同样求得 sigma 的平方等于三点八六七四。 然后计算期望收益率方差区限,定义两个长度为六百,取值为零的向量 sigma 平方 v 负值 diox rose 六百 e r p v 负值 diox rose 六百定义循环函数 for i 等于一到六百 e, r, p。 负值负零点二,加 i 除以一千五,调用 f, m, i, n, c, o, n 得到权重 w, w 负值 w 的转制 计算 a, b, c, d 计算 sigma, 然后存入 sigma 平方 v 项量,将 erp 存入 erpv 项量,最后用 pro 函数绘制。
 01:00查看AI文稿AI文稿
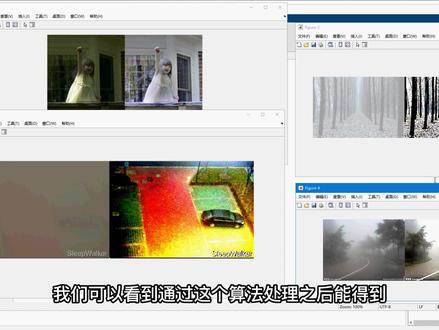
01:00查看AI文稿AI文稿大家好,这里是简简单单做算法,今天我们介绍基于多尺度 retinax 图像去污算法。首先将当前文件夹设置为程序所在路径,我们打开 me 函数运行。 我们这里提供了四个不同干扰程度的图像样本, 它的处理结果分别如下。那么第一个,干扰比较小的情况下,我们可以得到清晰的去污效果。第二个,雾气干扰非常严重,通过这种方法也能得到一个较为清晰的去污效果。 第三个,第四个样本是正常情况下的雾霾干扰,我们可以看到通过这个算法 处理之后能得到一个较为清晰的处理效果。演示完毕,谢谢大家。









