怎么做三角形垂直平分线锐角钝角直角
粉丝15获赞58
相关视频
 01:28查看AI文稿AI文稿
01:28查看AI文稿AI文稿尺规作图画角平分线,线段垂直平分线并作圆。已知三角形 a、 b、 c 求作圆 o, 使它经过点 b 和点 c, 并且圆心 o, 在 角 a 的 平分线上保留作图痕迹。 圆心在 b、 c 的 垂直平分线上的圆就过 b 和 c, 并且作角 a 的 平分线,交 b、 c 的 垂直平分线于一点,这个点就是满足条件的圆心 o。 可以先做 b、 c 的 垂直平分线,这里记为 e、 f 就是 分别以 b、 c 为圆心,以相同的足够的长度为半径做两道弧,相交于两点,过这两点做直线,就是 b、 c 的 垂直平分线。 然后作角 a 的 平分线,交 e、 f 于点 o, 就是 以 a 点为圆心,以适当的长度为半径作弧,各交角 a 的 两边于一点,再以这两点为圆心,以相同的足够长的半径分别作弧,交于一点作点 a 与这个交点的射线 就是角 a 的 平分线,交 b、 c 的 垂直平分线于点 o 连接 o, b 就是 圆 o 的 半径。 最后以点 o 为圆心 o、 b 为半径作圆 o, 图中圆 o 就是 所求。最后,这个结论不能少,当然更不能只写结论不画圆。你以为我是开玩笑的吗?不,我是亲眼见到的。
 03:31查看AI文稿AI文稿
03:31查看AI文稿AI文稿深农教育张老师今天带你涨知识,我们今天呢,通过一个视频把全等三角形中的三垂直模型给同学们讲解清楚来,首先我们先看一下题目啊,如图,角 a、 c、 b 等于九十度, ac 等于 bc, 我 们给它标一下,这是 bc, 这是我们的 ac 啊, ad 垂直于 c、 e, a, d 垂直于 c、 e 啊, b, e 也垂直于 c、 e 啊,垂足分别为 d, e 啊。现在已知 a、 d 等于三,我们的 d、 e 等于二,问我们的 b、 e 等于多少啊?这个题呢,其实非常的简单哈,所谓的三垂直模型是什么呢?就是我们来看我们这个题目中 有三个垂直的角,对吧?一个 a、 c、 b 这个角,以及我们的 c、 d、 a 和我们的 b、 e、 c, 对 不对?我们有三个垂直的角,这三个垂直的角可以干什么呢?来,我们有三个垂直角,我们可以得到, 比如说 b、 c、 e 这个三角中我们可以得到这个角,我们设为角一啊,这个角我们是不是等于九十度?角角二我们可以得到角一加,角二 等于我们的九十度,对吧?同样的,这个地方有一个直角三角形,我们是不是可以通过这个得到角二加这个角,角三是不是也等于九十度? 好,这个地方同学们就发现了,我这个角加它是九十度,这个角加它是九十度,那我角一是不是就等于我们角三?通过这两个地方,我们是可以得到 我们的角一等于我们的角三来,同理哈,我这个地方是垂直的,对不对?那我这个地方角三加这个角是不是也是九十度?我们设为角四,那我的角四是不是等于我们的角二呢?啊?我们同理哈, 我们可以得到我们的角四等于角二的。也就是说,如果我有三个垂直的模型,我们可以干什么?那我们就可以通过这三个垂直就可以得到转换出角度的一个相等的情况,这就是我们所说的 三垂直模型,对不对?我们通过三垂直模型,我们得到角度相等,我们需要证明三角形全等,我们需要什么?是不是需要一条边的调节?也就是说,我们题目中的 a、 c 等于 b、 c, 那 我们就可以很轻松地证得我们的 b、 c、 e 全等于三角形,我们的 c、 d、 a 对 不对?那我们就很轻而易举的能得到啊,这个地方, c、 e 等于我们的 a, d 等于三,对吧?以及题目中说的 d、 e 等于二,那很简单,我们的 c、 d 就 等于多少三减二等于一是吧?那我们 b、 e 是 不是就也等于一?那这个题我们就结束了啊?同样的,我们的三垂直模型是不是就意味着只要有三个相等的角,它们共共一个顶点,我们是不是就可以得到 啊?角度相等的情况下,当然我们出题目也不可能说是只出这么一种,对吧?包括我们这样的 一个垂直,然后从中间过一条线,如果我们得画两边的垂直,我们是不是同样的可以得到这个角度等于我们的这个角度 啊?这个角度等于我们这个角度啊?三垂直模型归根结底呢,就是我们的一个角度的转换,当我们看到有三个相等的角的时候,我们去利用角度的转换,是不是就可以得到其他相等角度的题目, 这样我们的三垂直模型的根本原理就被我们已经牢牢的掌握住了。
16昇龙教育张老师 01:31查看AI文稿AI文稿
01:31查看AI文稿AI文稿尺规作图画,角平分线,线段垂直平分线并作圆。已知三角形 a、 b、 c 求作圆 o, 使它经过点 b 和点 c, 并且圆心 o 在 角 a 的 平分线上保留作图痕迹。 圆心在 b、 c 的 垂直平分线上的圆就过 b 和 c, 并且作角 a 的 平分线,交 b、 c 的 垂直平分线于一点,这个点就是满足条件的圆心 o 可以先做角 a 的 平分线,就是以 a 点为圆心,以适当的长为半径做弧,各交角 a 的 两边于一点, 再以这两点为圆心,以相同的足够长的半径分别做弧,交于一点,做点 a 与这个交点的射线就是角 a 的 平分线。 然后做 b、 c 的 垂直平分线,就是分别以 b、 c 为圆心,以相同的足够的长度为半径做两道弧,相交于两点,过这两点做直线,就是 b、 c 的 垂直平分线。 角 a 的 平分线与 b、 c 的 垂直平分线的交点,即为点 o 连接 o, b 就是 圆 o 的 半径。 最后以点 o 为圆心, o、 b 为半径缩圆 o 可以 在 b 点和 c 点上瞄点,以掩盖细微的误差,误差太大就是错误,那可不行,不要忘了写上结论解如图,图中圆 o 就是 所求。
 03:14查看AI文稿AI文稿
03:14查看AI文稿AI文稿大家好,今天我们继续学习几何模型,今天要讲的是垂直平分线模型。什么是垂直平分线模型呢?当题目条件中含有垂直平分线,或者是有两个点,关于某条线是对称的, 则此时就用垂直平分线模型,只要将中垂线上的这个点和线段两岸进行一个连接,从而构造一个等腰三角形。 看一下模型图,如图所示的 o p 垂直平分 a b, 或者说 a b 两点,关于 o p 这条直线是对称的, 那遇到这类题目时,我们辅助线通常是将 pa 和 p b 分 别进行直接相连,从而构造一个 等腰三角形,就能得到以下结论, pa 等于 pb。 第一个结论,在证明过程中,我们其实是可以直接拿来用的,为什么呢?我们可以根据垂直平分线的一个性质,垂直平分线上一点到线段,两段的距离是相等的, 所以就能得到 pa 等于 pb。 那 具体证明如何去证呢?我们来看一下,也是通过全等来证的。 因为 o p 垂直平分 a b, 所以 就有 a o 等于 b o, 角 p o, a 等于角 p o, b 等于九十度。 那在三角形 a p o 和三角形 b p o 中, a o 等于 b o。 找三个条件,然后还有两个角相等,即 po, a 等于角 po b, 那 还有一条公共边 po 等于 po, 所以 根据 s a s 及边角边,就能证出 a, p o 全等于三角形 b, p o 边角边 全等。之后就能得到对应边相等及 pa 等于 pb。 第二个结论来证明等腰三角形 pa 三线合一。什么是三线合一呢?那你要搞清楚,所谓的三线是指垂线、 中线还有角平分线,这三个线合成了一体,所以也就是只要证出这两个角相等而由一可得,对应角相等,所以角一等于角二, 那角一等于角二了,所以 o p 为角 a p b 的 角平分线, 那还要写上 o p 垂直平分 a b, 所以 这个等腰三角形 p a b 三线合一好证明,就是 根据全等三角形的边角边,从而得到对应边和对应角相等。好,今天的垂直平分线模型就录到这里,下期视频我们再见。
10会教数学的小陈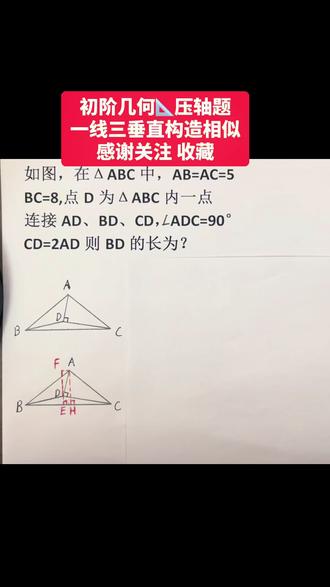 04:49查看AI文稿AI文稿
04:49查看AI文稿AI文稿大家好,之前讲过一线三垂直的技巧和利用一线三垂直勾到全等三角形的立体。今天再来做一道利用一线三垂直勾到相似的几何体。如图,在三角形 abc 中, ab 等于 ac 等于五, bc 等于八 点, d 为三角形 a、 b、 c 内一点连接 a、 d、 b、 d、 c、 d 角 a、 d、 c 等于九十度, c、 d 等于二倍的 a、 d。 求 b、 d 的 长度。这道题怎么做?咱们先利用已知条件,把能计算出来的线段计算出来, a、 b 等于 ac 等于五,这是一个等腰三角形,底边等于八,底边上的高很好算出来,底边的一半等于四。根据勾股定律,三、四、五底边上的高 a、 h 就等于三。题中又告诉我们,三角形 a、 d、 c 是 个直角三角形 a、 d 比上 c、 d 等于一比二,斜边等于五, a、 d、 c、 d 也能算出来 a、 d 就 等于根号五, cd 等于二倍的根号五。 接下来怎么做?求 b、 d 的 长度。常规思路应该把它放在一个直角三角形里。咱们做 d、 e 垂直于 bc 交, bc 于点 e, 我们就构造了一个直角三角形 bde, 求出来 d、 e 和 b、 e 的 长度,就能算出来 b、 d 的 长度了。这时候我们观察发现, d、 e 这个线段跟两个直角相连,一个是 a、 d、 c, 一个是 d、 e、 c。 同时呢, c、 d 是 a、 d、 c 的 一个直角边。我们又知道 a、 d 和 c、 d 的 比例关系, 这时候我们联想到利用 a、 d、 c 的 另一个直角边去构造相似三角形,也就是一线三垂直。我们做 a、 f 平行于 bc 交 e、 d 的 延长线与点 f, 这时候 a、 f 也就垂直于 ef 了,也就垂直于 d、 e。 三角形 a、 d、 f 就 相似于三角形 d、 c、 e。 为什么呢?因为角 a、 d、 f 和角 c、 d、 e 互余,它们俩相加,等于九十度。那这两个直角三角形的三个角就相等了。同时呢, a、 f 平行于 bc, 那 e、 f 就等于 a、 h 就 等于三,因为平行线之间垂线段相等。根据三角形 a、 d、 f 和 d、 c、 e 相似,我们可以推出来, d、 f 比上 c、 e 就 等于 a, d 比上 c, d 等于一比二。 我们假设 d、 f 等于 x, 那 d、 e 就 等于三减 x, c、 e 呢,就等于二 x, c, d 呢? c、 d 的 平方就等于 d、 e 的 平方,加上 c、 e 的 平方 c、 d 我 们知道,等于二倍的根号五,把 x 带进去, x 求出来,就等于五分之十一。 这时候 d、 e 就 知道了,就等于三减五分之一等于五分之四, b 就 等于 bc 减 c, e, c、 e 等于多少呢? c、 e 等于二, x 就 等于八,减去五分之二十二,就等于五分之十八, b、 d 就 能求出来了,就等于根号 d、 e 的 平方加上 b、 e 的 平方,就等于 五分之二倍的根号,八十五。
 15:45
15:45










