转动惯量计算公式微积分
粉丝2870获赞3.0万
相关视频
 42:13
42:13 05:10
05:10 01:29
01:29 00:20查看AI文稿AI文稿
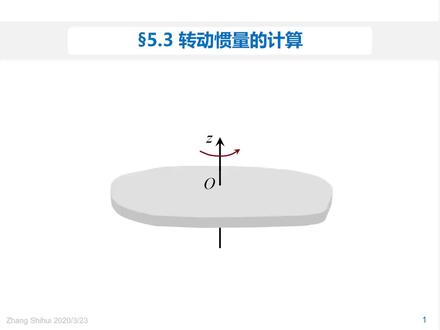
00:20查看AI文稿AI文稿转动罐量怎么快速计算?长方体罐量圆柱转动罐量公式, 空心圆柱冠量、直线运动冠量不通过重心的冠量、各种冠量的自动计算。
 04:35查看AI文稿AI文稿
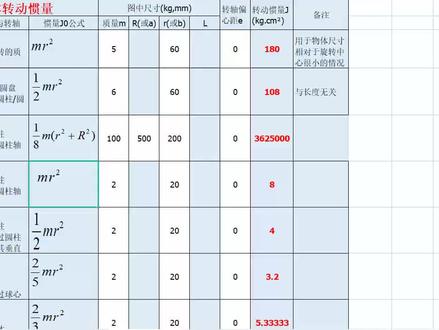
04:35查看AI文稿AI文稿啊,给大家讲一下转通挂念的一个计算啊。啊,通常来说我们用的比较多的就是呃前面这四种吧啊,其他的话用的很少 啊,在用的时候呢,首先第一种的话就是绕着我们这个自行旋转的啊,通常来说比如说这个是一个转盘里面的话有很多弓箭的啊,那么这个时候的话我们就是通过他的一个转动的一个情况呢啊, m 这个啥啊?这平方就可以计算出他哪个挂量的啊?这第一个哎妈的平方呢?那你填写这个参数就可以计算了。 好,那么第二个的话就是什么呢?就是这个圆柱或圆盘之类的 m 二分之一 m 二的平方啊,填写参数一样的,比如说这一方是啊五千克啊,他的半径值是四十啊,那么就可以得到他的挂量 知道吗?好,那么在做的时候的话建议看的有全套的一些系统课程啊,包括自动化的一个计算,包括计算里面的结构设计啊,都有啊,然后气动结构设计,气动啊结构还有各种电机,还有外购键,还有各种按钮设备之类的,学生的话也可以做这个飞镖设计啊, 然后这一方的话就说的一些视频模型啊啊,每天发的都有啊,辅助工具的包含了各种电机,液压,气动,还有各种结构的一些选型,然后这边的话有三千到四百模型各个行业啊都有都是呃,都是呃 啊,分类好的,然后可以下载边角好,那么来看一下他怎么去呃其他的一个方式好吗?啊,像这种薄皮的话就是 mr 的平方,就是你的这个质量是多少对不对啊?然后你的转动半径是多少啊?的平方就等于转动挂量好,那么我们在做的时候的话,尽量的把这一个单位的话统一 一样,我们在做的时候如果说你是千克的话,就同一千克的啊,这个米的话就用米每秒去计算,就是我们在用的时候选电机的时候,你不是要有挂量吗?那你这个样测,如果说是毫米就用好米计算,如果说是米就用米计算,知道吧? 啊,那么其他的话这一些呢,其实用的比较少,如果说你用的话,你也可以直接填写这个参数,也可以去选择的,因为你在做的时候你像这个呃,薄形体带从中间旋转啊,这个球体对待,还有这种圆柱体从中间旋转,还有这个从侧面旋转带,这种的话其实用的偏少啊,偏少 好,那么还有一种的话最常见的就是他,他用的一些机构啊,这个机构的话我们在使用当中呢,他是有什么呢啊?最常用的就是比如说这种皮带啊,链条啊啊,下面驱动一个物体,或者说我们啊这种此轮此条之类的啊,都是可以用这种防。 是的啊,通常来说呢,他的计算公式也是一样的, mr 的平方,出于这个效率啊,那么在做的时候,比如说我们这个下面输送的物理物体是呃,五千克,对啊,那么就是 m, 是不是啊?那么我们乘以什么呢?乘以啊啊的话就是我们的一个主动轮,是不是啊啊的平方啊,就是等于我们这个灌量啊,那么在做的时候你拿的就是这样的话,这一方有质量对不对?有这个从东轮的一个,呃,这个长度的,然后这边有这一个效率啊,就可以等于我们这一个灌量了。 好,后面的话我们这边的有四缸,四缸的话我们在使用当中呢,也是有这个常见关量的,一般来说就是通过什么呢? m 啊,乘以什么呢?乘以这个 p, p 的话是倒乘啊,就是我们一转到一圈走的一个距离,除以什么呢?二派,二派的话是,呃,就是这个什么?就是派, 就是拍,就是等于这个半径直接一样的的平方啊,就等于这个等于这个挂量,那么你填的时候也是一样的,填这个参数就可以得到得到我们这个挂量,知道吗?啊?后面的话在做的时候这个挂量当中呢,还要注意一个问题,就是比如说,哎,我这个电机对不对 啊?那么这个电机的话驱动的一个减速机来,那么这个减速机呢?再带动一个四缸,好,那么四缸,比如说算出来这个总共质量是十五千克的啊,十五啊,千克每平啊,那么这个时候我们这个电机的挂量在匹配的时候呢,一定要处于这个减速机的传动比 啊,比如说这个转墙传动笔是五,那么就是五的平方,那么这个时候的挂量再去匹配啊,大家可以看到就是挂量,对不对?处于这个传动笔啊,是不是啊?然后就等于用这个电机时机的挂量,因为增加这个减速机的话, 他也可以增加你的这个啊挂量的一个匹配,知道吗?啊?包括这个什么?包括这个皮带也是一样的,对待链条、齿轮都是一样的啊,都是要乘以一个啊,这种,就是 啊,都是要乘以这个,就是啊,出于这个啊,传动比的平方啊,这边的话也有这个效率啊,效率的话大家可以根据这个地方填。
550非标机械设计学习 01:26查看AI文稿AI文稿
01:26查看AI文稿AI文稿本期我们详细学习等效转动灌量的计算,感兴趣的朋友请点赞、关注、收藏!什么是等效转动灌量?举个例子,一个冠心质量是按 瞬时速度为 b 的物体,它的动能是二分之一乘以 m 乘以 v 的平方。另外一个转动灌量为 j, 瞬时角速度为 w, 绕轴转动物体,它的动能是二分之一乘以 j 乘以 w 的平方。如果这两个动能相等,那么我们认为这两个运动在能量上是等 消。绕轴转动物体的灌量可视为平动物体的等效转动灌量,反之亦然。等效转动灌量的前提是动能相当破手逢。我们以私跟机构为例,来推到私干负载的等效转动灌量。 我们假设四伏为匀速角,速度为八维,丝杆负载的惯性质量为二,线性速度为力,丝感的逻辑为 b。 根据丝感的结构,我们 赐福电机旋转一周,斯感负在运动一个逻辑。因而我们可以得到以下关系,力除以刀,不用等于 p 除以耳畔。但入到我们前面的等效转动灌量的公式,就可以求出等效转动灌量的计算公式。翻开米斯尼电子行路两千八百三十米, 其中负载惯性例局和我们推导出来的公式是一致。任何复杂机构的等效转动灌量的计算也是同样的方法,我们只需要找出等效机构和被等效机构的速度变成关系。本期视频就到这里,喜欢的话还请关注、点赞、收藏、转发给你的朋友,谢谢您的观看!
559FlyDream机械 00:50
00:50 00:35
00:35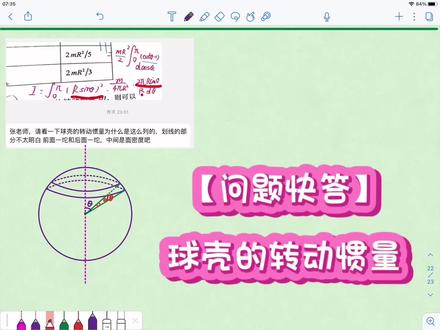 12:10查看AI文稿AI文稿
12:10查看AI文稿AI文稿好,咱们来看一下啊,你问的是这个问题,就是这个划线的部分,划线的部分不太明白前面一坨和后边一坨是什么东西啊? 我就把这个过程给你推一下,我们看一下这样一个球壳的转动换量是怎么来推的,我估计你也是刚开始学,所以说不是很熟悉啊。首先啊,我们明确一件事,就是一个东西的转动换量, 如果它是一个连续体的话,我们直接用积分,这个地方应该是 d m 再乘以 r 平方。明确什么意思呢? d m 相当于是我们把 这样一个物体的质量,按照相对于他转轴比较好积分的形式把它切割,然后这个耳的小耳的平方指的什么东西呢?小耳的平方指的是你 切割的这一小部分质量距离转轴的这样一个垂直距离,明白这样一件事吗?那么对于这样一个均匀的球壳,我们一般怎么切呢?我在这地方已经画了一个图啊,我一般情况下切的方法不唯一,但是我们一般情况下可以这样来切。 其实还有别的切法啊,但是计算起来可能不如这个简单啊,我们怎么来切呢?注意,这是一个均匀的球壳,我们可以把它像削苹果一样啊,削苹果一样,把它给它削成相当于一片 一片的这样一个东西啊。你比如说我在这个图中,我相当于我取的一个 dm, 一个小质量的致元,相当于就是这样我切出的这么一块东西,当然这边还有这样一些东西啊,这样一个环带相当于是我取的 dm。 那么我首先啊,我就先去表示这么一个 d m, d m 应该等于什么东西呢? d m 是不是应该等于它的面密度? c 个码再乘以这一个 d m 所对的表面的 d s, 因为我们说它是一个薄球壳,不考虑它的厚度, 是这样的吧?好,那么 c 个码等于什么东西啊? c 个码很好,表示 c 个码应该等于总质量 m, 再除以一个呃,球体的这样一个表面积,就是四 pa, 再乘以耳平方这个大耳就是题目中给的这个半径吧, 对吧?关键我们就是去表示 d s 就行了。那么 d s 可以怎么表示? d s 可以怎么表示? d s 是不是我切出的这样一个还贷的这样一个面积?那么这样一个还贷的面积,它其实是非常窄的一个还贷。你看一下它这是一个还贷。 还贷的话我是可以把它打开,把它打开的话,实际上打开以后他应该是长成什么样呢?实际上打开以后他应该长成这个样,他应该长成这个样,他不是一个严格的矩形。注意啊,他不是一个严格的矩形, 他的上下两个边应该是不一样的,对不对?上边应该是二帕,再乘以一个比较小的这样一个半径, 是他的上边,而他的下边的话应该是二帕,再乘一个尔比较大的这样一个大的这样一个半径。因为他上边一圈要小一点嘛,下边一圈要大一点。但是注意我们取的这样一个宽度是非常小的, 那么如果取这个宽度非常小的话,你把它真正当成它实际上是一个梯形,你把它当成 一个矩形去算的话,他相差的是不是应该就是这么一个,你比如说我把它当成一个大矩形去算的话,他相差的是不是应该是这两块小的三角形的面积啊? 这两块小的三角形的面积,你想一想,他实际上应该是一个高阶无穷小量,因为他的两个边长,这两个三角形,他的边长都是无穷小量,那么在求他面积的时候是不是无?会不会出现无穷小量?乘以无穷小量,他肯定就是无穷小量的平方,我们就认为他是高阶无穷小量,可以把他给略去。 什么意思?总而言之就是他虽然是一个梯形,但是实际上我们可以把它当成是一个矩形去算。那么对于这样一个矩形来看的话,我们看一下啊,如果当成是一个矩形来看的话,比如说我就把它当成是 一个小的,我把这两块都给他去掉啊,我把这两块都给他去掉,哎,我把这两块都给他去掉。我刚才已经说了,其实这样一个矩形和这样一个梯形和这样一个小的矩形, 我们可以把它认为面积是相等的。如果你真的取的是一个无穷小量的话,这两部分面积也是无穷小的,我们可以把它略取,那实际上它的面积就相当于什么东西呢?可以认为是。 你看一下这边长度啊,这边这边长度或者这端的长,这一段的长度应该是什么东西呢?应该是 r 再乘以 dc 他吧。 如果是尔乘以 d c, 它的话,是不是相当于我这样一个矩形的宽?就是尔再乘以 d c, 它没问题吧?然后它的长取的是哪个呢?嫦娥可以用 取这个上边的这个短的这一个边来算的话,短的这个边来算的话,那你看一下应该是多少?应该是多少?我在这个图中标了这样一个角度,是 c 塔,我取的是这一个位置标这个角度是 c 的话,那你看一下 我再用一个绿色的吧,绿色的这个长度是多少?这个长度应该是多少?这个长度是多少? 注意一件事,这个长度是不是应该是上边这个小圆的半径呀?这个长度就应该是 r, 再乘以个三 c 他吧,二,再乘以个三 c 他,所以说他的 这个是这个矩形啊,矩形他的长就应该是二 pa, 再乘以二,再乘以个三 c 他,这没问题吧?好,那已经都把这表示出来的话,那个这个矩形的面积应该是什么东西啊? 矩形的面积不就应该是咱们所说的二 pa, 再乘以 r, 再乘以个三 ct, 再乘以个 r, 再乘以个 d ct, 这就应该是它的面积吧?这就是它的面积 这个问题吧。就它的面积,那你就把它往里头带呗。往里头带,我就把它换成一个积分的符号 i, 应该等于注意我们的积分变量是 c 的, 我们的积分变量是 dc 塔啊,那你看一下我去积的话,是不是应该是从这个位置?从这个位置你看 c 塔,我想去积整个球壳的话, 因为我把秋壳都给他换成这样,每一还贷,每一还贷的话,是不是相当于从这一点要积到这样一点,就相当于把所有的这样一些还贷全部给他积出来了?从这一点 击到这一点的话,那很显然 c 他就应该是从零击到 pa 嘛。那你就写成这个地方就是零到 pa, 然后我们带进去呗,带这个 d、 m, d, m 是什么东西? d m 就是咱们所说的 c, c 个码就是 m, 再除以一个 四 pa, r 平方,再乘以 d, s 就是二 pa 再乘以 r, 再乘以三 ct 再乘以 r, 再乘以 d c, t 是不是应该还在乘一个 r 平方呀? 是不是还得乘一个小耳的平方?小耳的话就是我们刚才所说的,你注意小耳指的是哪一段, 小耳指的就应该是刚才我已经说了,这个质量圆啊,质量圆到达转轴的距离,那不就是咱们所说的这个大耳 再乘一个三 c 括号的平方吗?是这样的吧,它其实就是这么一个东西啊。那你对比一下你要问的东西啊,你要问的东西我们看一下啊,你对比一下你要问的东西,你问的是这个东西和这个东西是怎么来的?那你对照一下,你看一下, 那不就是我们这个地方,我们这个地方就出现了二 par 乘以三, c 再乘以二,再乘以 dc, 就是你问的这一部分 后半部分,那前半部分呢?就是这一部分了,对吧?然后接着其实你问的问题我已经解决了啊,我再把这个给他算完啊,把他给算完,这地方是 零 high, 这地方呢?把该扔的给他扔掉。你像这个地方有二平方是吧?二平方就去掉了,对吧?二派给他去掉,是不是只剩一个 二?所以说呢,我们再写一步吧,直,直接不再写那么多了,直接把这个长数给他提出来就完事了啊。这地方我们可以把长数给他提出来,就这个地方就是二分之 m, 这个地方呢?还有一个耳平方,后边啊,后边还有个耳平方, 对吧?然后里边剩下一个什么东西呢?剩下积分是零到派,再乘以个三 cit 的三次方,再乘以 dct, 这积分怎么积分呢?因为你是这个初学,你可能不太熟悉,我给你写多一点,写多一点啊,写多一点。 这个地方我要对他积分的话,其实他是有一个固定公式的,他是有个固定公式的,我们在这地方没必要再讲这个固定的积分公式,他分基偶性啊,基偶性有个固定的这个 n 四方,如果是分基偶性,他会有个固定积分公式。没必要啊,我们在这地方直接去。 在这地方呢,我可以直接把一个三 c, 他给他拿到积分符号里边去变换一下,就是二分之 m, 再乘以二平方,这地方零到 pa, 这地方我拿一个进去。靠,这 说错了,这地方拿一个进去,这个地方应该是三平方 c, 他拿进去以后是不是应该是 d call 三 c, 但是你拿进去以后是不是多了一个负号?所以说前面我要加一个负号啊,前面这个地方要加一个负号,然后再进行一步变形负二分之 m。 其实如果你比较熟练的话,直接就可以去写答案了,真的你熟练很很多以后就可以直接写答案,但是因为是不太熟悉的话,我就把它多写几步啊。这个地方是不是利用一个一减去 call 三的平方 seat, 一减去靠三的平方 seat, 再乘以 d call 三的 cat, 这个地方其实就是用换元了吗?因为是初学的话,所以说我就多写几步,我现在可以令 call 三 c, 他就等于 x 的话,如果令 call 三 c 等于 x 的话,注意他的积分上下线是不是就变了呀?我们知道如果这个 c 他是属于 零到派的话,或者说你积分是不应该是俗语啊?不应该写的是俗语。你 c 的积分是零到派的话,那你对应的这个 x 积分就应该是,呃,这个,这个,这个零就是一对吧,这个就是负一对吧?你积分上下线就变成一到负一吗?就你积分上下线了吧, 这个地方就是负二分之 m, 再乘一个二平方,这个地方就是一负一,这个地方是一减去 x 平方,这个地方是 d x, 对吧?然后你 就用一下那个牛来公式吗?牛顿莱布尼斯公式,这个地方是二平方,这个地方呢?就是我想想直接写吧,直接写这个地方就变成了 x 减去三分之 x 的三次方,这是积分的常见的公式啊,这个咱们得熟。这个地方呢,就是一到负一, 然后就算一下呗,负二分之 m 再乘以二平方,这地方就变成了这个,这个是一减去, 这是负一啊,负一减去就变成加上了三分之一,然后这边呢,再减去一个一,再减去一个三分之一, 那里边我们看一下等于多少。这负二负二,再加上三分之二,就是三分之四。负三分之四,负三分之四跟前面这个还有一个符号,就变成了 二分之 m, 写,再写一波 r 平方,再乘以一个,这个地方是负三分之四,结果就应该等于三分之二倍的 m, 再乘以 r 平方,我们就把它解决了,是吧? 关键就是这个积分啊,积分我们怎么去找这个积分变量?我们确定积分变量是谁,然后怎么去表示这个 dm? 当然你是要去表示 ds, 我就把它搞定了。
106杠精学物理 00:32
00:32 03:35
03:35






