凉山州中考中三角函数
同学们好,我是数学华子老师,带领大家一起冲刺中考数学。今天咱们讲三角函数,那么三角函数大起呢?作为咱们中考必考的一道大起, 在这个地方,同学们已经定好掌握了他的核心,也就是说三角函数 它的实质就是了解直角三角形, 那么咱们根据了已知角和已知边,在直角三角形当中列出了它的三角函数关系,这样的话,哎,说已知角 和已知边哎列了三角函数关系,然后求未知边 和未知的角,那么一般呢,他都是呢,哎,让你学未知边好,那么咱们由这道题呢进行讲解。 看题目说,学校运动场的四个角有一盏探明灯,其中一盏灯 b 的 位置呢?如图所示,已知 坡长 a c 等于十二米,坡角阿尔法为三十度,灯光射灯照的影响最远端的光线与地面的夹角贝塔为二十七度, 最近段的光线恰好与地面交汇了,坡面的底端 c 处,且与地面的夹角为六十度, a、 b、 c、 d 在 同一水平面上。 那么告诉了你一些啦,这个角的三角函数值,第一问让你求哎登高 a、 b 的 高度,第二问求 c、 d 的 长度。好,咱们首先呢看第一问, 那么在这个地方,咱们知道这个 d 点了 b 点了它是这个,哎,它是灯,那么 a、 b 就是 它的这个了,哎,灯杆 a b, 那么怎么去求它的长,这个长度呢?这个地方,哎,首先呢,咱们要把它放在三角形当中,也就是说我们知道了凹法,这个角是三十度,那么这时候咱们可以来延长 d, a 对 交这个地面 cd 于点 m, 那么我只要求出了 b m 的 长和 a m 的 长了就可以,那么也就是说延长 b a, 将 d c 与点 m, 那么这样的话就可以得到这个 b m, 则 b m 它是垂直这个哎, d c。 然后呢,在 r t 三角形 a c m a c m 中,这个角阿尔法等于了三十度, a c 等于十二,那么所以啊,这时候就有啊,哎, am 比上一个 a c, 它等于上引了三十度,哎,结, i m 比上一个十二,等于二分之一,这样的话,咱们就能够推出,嗯,能够推出什么了? i m 它等于六, 那么接着看 i m 等于六,哎,同理, 这个 c m 比上一个 a c, 它等于 cosine 三十,那么这样的话,推出 c m 比上一个十二,它等于二分之根号三,那么推出这个 c m, 它等于六倍根号三。 那么现在呢,咱们要求 ab, 也就是说我只要把 bm 求出来哎,就可以了, 那么 bm 怎么求现在呢?哎,咱们知道的是角 alpha 是 三十度, 而他说了这个呃 b 点与 c 的 这个夹角,哎,因为角 b c m 等于六十度。那么这样的话,在 r 七三角形 b c m 中,咱们是不是有这个 b m 比上一个 c m 等于弹琴,它六十度,其,哎, b m 比上一个哎六倍,根号三等于根号三,这样的话,推出 b m, 它应该等于十八,所以 ab 它等于 b m 减去 am, 它等于了十二, 所以说,哎, am 的 长,呃, ab 的 长是十二米。那么接着看第二步, 第二呢,它让你求 cd, 那 么咱们知道贝塔呢,它是二十七度,而且咱们知道 dm 的 长,所以说这个地方咱们呢可以求出了 dm 的 长。也说,哎,在 r t 三角形 b dm 中,哎,这个 b m 比上一个 dm, 它等于了碳氢碳二十七度,呃,截十八,比上一个,呃 dm, 它约等于, 约等于,哎,它的二十七度是零点五一,那么这个时候咱们就可以了,把 dm 了,给它求出来,哎,那么 dm 借得, 哎, dm 这个约等于多少?那么这个地方同学们呢,可以用计算机了,把它算一下, 那么接着看,那么 dm 求出来了,而咱们要求的是这个 cd, 那 么 cd 呢?等于这个,呃, dm 减去 cm, cm 呢?是已知的,那么哎,因为 c d 等于 dm 减去 cm, 它就等于多少?好,这个时了,就等于把 dm 了,咱们要算出来,这个时候可以用计算机了,可以把它算一下, 十八除以零点五一, 三十五点二九,三十五点二九,三十五点二九,减去 c m, c m 是 六倍根号三,那么六乘以一点七三, 哎,他约等于了十点三八,那么这个时候他应该约等于他应该等于多少了。另外这个地方说了,结果呢,要精确到零点一米,所以说,哎,他应该等于这个 约等于这个,呃,十四点九 米。好,那么这时候 c d 的 长度呢?就求出来了,也是答,哎,这个 c d 的 长为十四点九米, 好,那么咱们可以看到,也就是说做这类型的题,咱们要把这个呀,它的边,尤其是它的什么已知边, 要放到已知角所在的直角三角形当中,哎,就可以求出了外支边,以及了哎,一些边的了,关系,好,那么这道题呢,咱们就讲到这。
粉丝1479获赞8115
相关视频
 09:41查看AI文稿AI文稿
09:41查看AI文稿AI文稿同学们好,我是数学华泽老师,带领大家一起冲刺中考数学。今天咱们看一下三角函数里面的哎,关于隐藏来求了物体的高以及以及了哎边长的一些题目, 那么咱们由这个题呢进行讲解。首先看如图,学校的旗杆附近有一斜坡,小明准备了测量旗杆 a、 d 的 高度,他发现当斜坡正对着太阳光时, 其杆 a、 b 的 影长恰好落在了水平地面和斜坡的了坡面上。此时小明测得水平地面上的影子长 b、 c 等于二十点二米, 斜坡坡面上的影子长 c、 d 等于二五点二米。太阳光 a、 d 与水平地面 b、 c 成三十度角。斜坡 c、 d 的 坡度为一比二点四,求其杆 ab 的 高度。 那么呢,咱们首先分析其目这个地方,其杆 ab, 它的一部分隐藏是 b、 c, 另一部分呢,它落在了这个 斜坡上 c、 d 上,而 c、 d 呢是五点二米,而且它告诉斜坡 c、 d 的 坡度为一比二点四球旗杆 a、 b 的 高。那么像这种旗呢,它还有一种旗形就是了哎这个地方了 哎有个楼房,然后呢跟前呢也有一个哎楼房,那么太阳光这样照射下来以后呢,它的一部分影子呢,会落到了哎这个楼房的哎 这个楼房的呢这个呃楼房上面,然后呢一部分呢落在了它的这个水平地面上。 那么这两种情况呢,也是咱们先要求,求什么呢?求这个隐藏哎所在水平面它的呢,这部分隐藏是多少? 然后呢进行解哎这个直角三角形来求这个它的高度 h。 那 么对于这个题目当中呢, 这个 c、 d 来说,哎,咱们呢,根据它的坡度就可以求出,哎,它在水平地面上的长度应该是哎或点 d 做它的高 dm, 那 么这个时候 咱们就可以求出了 c m 和 dm 的 长,然后呢,它要求的是 ab, 因为呢, ad 与水平面的夹角上这个三十度,所以说我们呢连接 ad, 连接 a, d 过点 d 了,做它的高,哎,那么这个时候相相交于 n, 那 么 哎,香蕉与 n b, n 就是 dm, 所以 说咱们只需要把哎这个 dm 还有了这个 d n 给它求出来,这样的话, a n 呢,我就可以把它解出来,所以说,哎,第一步解它, 哎,过点 d 座 dm 垂直 bc 交 bc 于点 m, 然后呢,哎,在 r t 三角形 dcm 中, 这个时候呢,咱们有 dm 比上一个 c m, 哎,它的坡度是一比二点四,那么咱们可以设了, 哎, dm 等于 x, 则 c m 等于二点四 x, 哎, 所以这时候就可以得到 x 平方加二点四 x 括号的平方,它等于这个五点二的平方,那么这时候咱们就可以了,把 x 给它解出来,解得 x 等于多少?咱们可以算一下,二点四的平方是五点七六 x 平方, 加上一个 x 平方,就是六点七六 x 平方,那么五点二的平方呢,它就是五点二,乘以五点二, 可以看一下,五二十五,二十六四零七二二七点零四,除以了六点七六, 嗯,这个地方四四六了,二十四四七二十八四六二十四四,那么说 x 平方等于四, x 应该等于二, x 等于二,把它解出来了。 好,那么 x 写出来以后,这时候,哎,所以这个 dm 它是等于 x, 它是等于二的,哎, 而这个 c m 呢,它是等于二点四, x 也是四点八米。 好,那么这样的话,这时候再啦,哎,过 点 d 错 d, n 平行 bc 交 a b 于点 n, 哎,则 哎,则什么呢?则这个 b n, 它就等于 dm 等于二。那么要求 a、 b 怎么呢?把 a、 n 算出来就可以了。那么 a、 n 怎么求? 现在呢,咱们知道这个 a、 d 与水平面所构成角是三十度,所以说 a、 d、 n 这个角是三十度,那么我求出 d、 n 就 行了。那么 d, n 呢?是不是等于 cm 加 bc? 哎, 因为又因为了 b m, 它等于 bc, 加这个 c m, 它就等于二十点二,加上一个四点八,等于了二十五米, 那么极,所以这个 d、 n, 它是等于二十五米。 那么在 r t 三角形 a, d、 n 中怎么就有啊?这个 a n 比上一个 d n, 它就等于贪心他了。三十度,哎,即 an 比上一个二十五,它就约等于,哎,它就等于了三分之根号三啊,那么这时候把它解出来就行,哎, 所以 an, 它就等于三分之二十五倍根号三,那么它已经告诉你了,根号三呢,取一点七三,那么咱们可以算一下, 二十五乘以一点七三除以了三,它是等于约等于十四十四点四米。 那么这样的话,哎,所以这个 a b 等于 an, 加上一个 b, n, 它等于十四点四, 加上一个。呃,怎么算出来的? d n 是 两米二,它就等于了十六点四,约等于了十六米。 因为题目当中呢,要求咱们保保留了精确到一米,所以说答了就是十六米。 好,那么像这是这是,这是呢一种类型,像我刚前面呢画的这第二种类型, 哎,这个呢,他落到墙上的这一部分呢,咱们也可以了,哎,去求这个直角三角形,先把 哎墙上落在了这一步呢,这个直角三角形求出来,然后呢再去切这个地方,哎,这个直角三角形。好,今天的课呢就讲到这。
 03:54查看AI文稿AI文稿
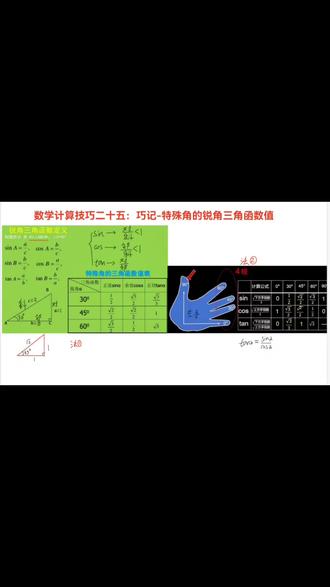
03:54查看AI文稿AI文稿大家好,今天给大家带来数学计算技巧二十五,巧记特殊角的锐角三角函数值。我们这里介绍两种方法,无论哪种方法,首先我们先搞明白锐角三角函数的定义。 初中所学的锐角三角函数都是在直角三角形 a、 b、 c 中,比如说这个直角三角形角 c 就是 直角,我们以 a 为研究, 那 a 所对的边叫做对边, a 旁边的两个边,一个叫做邻边,一个叫做斜边,斜边是长的。那正弦的定义就是对边比斜边,对边比斜边。 余弦的定义就是邻边比斜边,邻边比斜边正切的定义就是对比邻, 对边比零边。搞明白之后,我们先用第一个方法去记忆法。一,就是我们要记住两个特殊的直角三角形,一个是这个,一个就是我们之前说的三角板。 那三十度所对的直角边是斜边的一半,我们假设这个小 a 是 一,这个斜边就是二。根据勾股定律,这个边就是根号三。 那我们看这个三角形既有三十度又有六十度,我们就可以记忆这个三十度和六十度的了。三十度是对边比斜边正弦,所以是一比二。 零边比斜边是余弦,二分之根号三,对边比零边是正切,一比根号三就是三分之根号三。 同样的方法我们可以记六十度。六十度的对边应该是根号三,比斜边比二,所以二分之根号三。 六十度的零边比斜边就是余弦,就是一比二。 六十度的对边比零边应该是根号三比一。记住六十度所对的边是根号三,四十五度的就比较好记了。我们比如说这个角是四十五度,他的对边就是一,一比根号二就二分之根号二 与弦呢?临边比斜边,因为它的临边和对边一样,所以都是二分之刚好二。四十五度的正切等于对边比临边,一比一就是一, 那么方法一,只要记住这两个三角形就 ok 了。接下来我们讲一下这个方法二, 这个方法二就是我们伸出自己的一个左手,我们规定这个从这个小拇指 零度、三十度、四十五度、六十度、九十度,大拇指是九十度。然后这个计算公式,比如说正弦的计算公式,就是二分之根号下下方手指的个数。 比如说我们要算这个三六十度,它下方手指是三个,所以就是二分之根号三。扩散就是上方手指的根号数。比如说我们要算扩散这个三十度,扩散三十度,它的上方手指是一、二、三, 所以是二分之根号三。那正切呢?其实就等于正弦比余弦。这里有个公式, 所以我们只要记住这个三和扩散这个正切,直接拿这个三除以这个扩散就 ok 了,所以这个正切就等于下方的手指数,除以上方的手指数,整个开根号。 大家觉得哪种方法更好一些?欢迎大家在评论区留言,感谢大家的聆听,关注老师了解更多数学计算技巧,我们下次再见!
24hhxx 11:31查看AI文稿AI文稿
11:31查看AI文稿AI文稿十分钟教会你!十七、求三角函数值,同学们好, 九下的第一张直角三角形当中的边角关系基本上已经写完了,在这一张中,有两种类型的题目在考试中经常出现, 一是求某一个角的三角函数值,二是三角函数的实际应用。那么今天的视频我们开始开始慢慢的解决这两种类型的题目。 那么首先看第一类要求某一个角的三角函数值,首先要看这个角是否在直角三角形中,如果在看能不能通过求线段的长度得到答案,如果不在的话,那就有两种方法, 第一种是构造直角三角形,让角在直角三角形中了。第二个是通过转化相等的角,让角存在于另一个直角三角形当中,从而得出我们所需要的答案。下面同学们看一个比较简单的题目,我们说这个第一题, 在矩形 abcd 当中, ad 这个边长等于五,我写在这 ab 这个边长等于四, 然后 e 是 bc 上的一个点,而且 b, e 等于三,那么当这个矩形的时候,这个角是九十度,那么三角形 a, b, e 的 两条直角边是三和四,那它斜边一定就是五个勾股数,那么然后 d, f 又垂直于 a、 e 与 f 点,那么三角形 a, f, d, e 也是一个直角三角形了,然后他要求某一个角的正切,这个角是 f, d, c, 很明显我们发现这个角它不在直角三角形当中,它是在一个四边形 d, f, e, c 当中,当这个角不在这样的一个 三角直角三角形中的时候,我们就有两种方法,而第一种方法我们需要去构造直角三角形,所谓的构造我们就指直去做负主线啊,就做垂直来构造出直角三角形, 好,这是第一点。第二点我们是要把相等的角进行转化, 就是转化成另一个角,然后呢我们说这就是当一个角不在直角三角形当中时候, 角,我写错了啊,不在直角三角形, 当角不在直角三角形中的时候,那么第一个是构造直角三角形,第二个就是把相等的进行转化,那么按照这个方法我们想想,那么这个角我们要求的这个不在直角三角形中,我们以这两种方法找哪一个呢?如果要构造的我肯定需要做负值线, 那么也就说我可以先看看在整个的图形中有没有一个角和它相等,我们会发现你看哈这个角加这个角应该等于九十度, 当这个角九十的时候,那么这个角加它也等于九十度,那么同角的与角相等,那么这个角肯定会等于这个角,因此要求这个角的正切,其实就求这个角的正切。 那有同学发现这个三角形当中要求他的正确等于对边比上零点,那么然后这两个这角边也不知道有同学继续转化上下矩形相等,然后呢内错角相等,那么也就说这个角跟他又相等, 那么咱就说这个角等于这个角再等于这个角,而这个角已经在了一个三四五的直角三角形当中,那么这个角的正切值等于对边比斜边,那也该等于四比上三, 四比上三。好了,这样的话我们就得出了答案,其实这个就是用的第二种方法,把一个相等的角进行了转化 啊,在转化的时候是转化了两次,那题会更加简单。还有些同学可能会用这样的方法,当他看到他是三、四、五的时候,这个只要三角形,斜边又是五。有些同学立马会想到,这两个三角形其实是全等的, 直角和直角相等,内错角相等,斜边相等,然后是 a、 a、 s 两个三角全等,这一全等,我们可以得出对应边相等,这个边应该是四,这个边应该是三,那么然后这个角的正切陇然等于四比三,那也说另一次全等转化一次角相等也可以。 那么这是我们所说的第一题。然后我们再看第二题,这个题呢,稍微的难度大一点啊。 这个题当中是在矩形 abc 中, ab 等于八,右边等于八, bc 边等于十二,就上面等于十二啊。 然后点一是 bc 边的中点,那么说明一块是六,一块是六中点吧,那这个地方是九十度六八,这个斜边肯定是十,这是没问题的。这些同学们在读题的过程中已经得出来了连接 ae, 然后他说把三角形 abe 这个三角形 沿着 a、 e 进行折叠,是 b 点落在 f 处,这两个三角形是全等的。所谓的全等折叠以后,远外之意就是这个边折到这是六啊,这个边折到这,这块应该是八,这是六,那么同样会发现,这个三角形竟然变成了等腰三角形, 哎,这个边是六,这个边也是六,所以他就是等腰了。这两个是直角啊,然后连接了 f c, 这里求三角 e c, f e c f, 就 这个角 要求这个角的正弦值啊,很明显这个角不在直角三角形当中,那么当角不在直角三角形,我们还应该考虑这两种方法到底是构造呢,还是用相等的角进行转化呢?其实对这个题来说,构造和相等的角进行转化都可以, 那么朋友们,我们如何把它进行相等的角进行转化呢?朋友们,你看啊,折叠的过程当中,这俩角是相等的,角一是等于角二的, 那么当这个边是六,这个边是六的时候,这俩角是三和四,是应该相等的 啊,这两个六和六相等,角三等于角四一折叠角一等于角二,那我们发现这个角我点问号的这个角它加角一,角二等于一百八十度, 那问号这个角加角三,角四也等于一百八十度,它是一个平角,它是三角形的内角。和同样我们可以得出角一加角二等于角三加角四, 角一加角二,你看哈,是角一加上角二,他俩相等,再加上问号,他应该等于一百八,这个一百八是角 三加上角四,也加上问号,他也是一百八。这样把问号约掉,我们会得出角一加角二等于角三等于角四,而角一又等于角二,角三又等于角四,这样我们还可以得出角一肯定是等于角四的 好,那么通过这种相等的角的转化,他说我们把角四这个角可以转化到角一这个地方来,那么求角 e、 c、 f 就是 角四角的正弦,也就是角一的正弦,那角一的正弦等于对边比上斜边等于八比十,然后就等于四比五。 好,那么这样我们就会得出了正确的答案,而这种方法我们用的就是相等的角进行转化。还有些同学他可能会想到我做负数线,因为什么呢?因为这个三角形已经是个等腰三角形了, 这个三角形已经是个等腰三角形。而我们最常见的负数线的方法,我们需要去从这个地方往这做垂直, 一旦做垂直以后,这是 em, 我 来垂直于 e c。 这个垂直有个最大的好处是把我们要求的这个角放到了一个直角三角形当中 啊,放到了一个直角三角形的,然后我们要求这个角的正弦就等于它对边比上它就行了,因此我们只需要去求出 em 的 长度,我们就可以比上六, 在这个角等于对边比斜边比上六,那么它就是我们所要求的角的答案 ecf。 所以 这个题就转化为求线段的长度, 而这个线段的长度,我们根据刚才的证明,角一是等于角四的,当然这个题从这地方说就拐弯了,那你能知道角一等于角四等于,当它折叠的时候,我们说这个折叠的时候, 很明显这个点应该是这个 b f 的 终点,而且呢,而且这个地方是垂直的关系, 就是 n 点是 b f 引含的终点,而且这个地方是垂直,而这两块距离啊,这两块距离可以求出来,就是当这个垂直实际上就是六八十的直角三角形的斜边上的高 啊,他这个地方也垂直六八十斜边上的高。利用等积法是怎么算的?是二分之一 乘以六,乘以八,等于二分之一乘以十,再乘以这个高 b n, 或者说这个 n f, 那 么我们可以得出 b n 等于六八四十八,再除以个十就等于五分之二十四,这样我们可以求出 b、 n 的 长度是五分之二十四 好,那么然后 b、 n 和 n、 e 是 相等的,而我们知道这两条线是互相平行的,一和四是相等的嘛,那么然后这块距离肯定是等于这块距离的,那么这两块距离的求法啊,相对来说,他拐了一个弯,就说你如果已经知道角 e 等于角四,这个题就没有必要去这样做了 啊,但是这个题却是一个很,就是如果我非要做高的方法的,我只能这样求啊,这块是五分之二,他就是五分之二十四,那么然后得出这块距离也是五分之二十四,然后这个地方就是五分之二十四, 去除以六啊,应该等于五分之二十四,去乘以六分之一,答案应该等于五分之四好,也就是等于三,这个角 e、 c、 f 好。 那么如果这个题非要用我们说构造这个直角三角形来解的话,这个题只能是这样解, 那么这样解反而就麻烦了,所以我们在做题的过程一定要去灵活的选择这两种方法,那么也就说这两个题我们都用第二种方法把相等的角进行转化,能够使这个题显得更加简单。好了,那么同学们今天的讲题到此结束, 谢谢!每周一到周五更新,每天一课,解决您和孩子的数学难题,如果你有任何的数学问题需要解决,欢迎私信答疑,点个关注吧!
16数学孙老师 24:12查看AI文稿AI文稿
24:12查看AI文稿AI文稿我们看五点二三角函数的概念,我们先回忆一下初中学过的三角函数,先看一下这个直角三角形,它是三四五码,然后三呢,就是它的对边比斜边就是三比五,然后 cosine 呢,就是它的零边比斜边是四比五, ten 呢,就是它的对边比零边就是三比四,那么这个是同样的道理,能求出它的这些值, 这个三角函数的大小,比如说 sin 的 alpha, 这个值的大小呢?它其实只是跟这个角的大小有关系,它跟这个三角形的大小是没有关系的吧?你可以看一下这两个三角形是相似的吧,那么这两个角肯定是一样大的, 对不对?你算出来的这个三引阿法,你这里是五分之三,你这里是啊,十分之六,化简之后也是五分之三,其他的都是同理的啊。所以我们这个三角函数的这个函数值, 它其实只是跟这个角的大小有关系,跟这些边的长度是没有关系的啊。好,那么我们来看一下高中对三角函数的定义,就是把它放到一个圆里面, 然后呢,这个是它的使边,然后经过旋转得到了一个中边,对吧?那么它的中边跟这个圆的一个焦点,我们记作为 p, 它有它的坐标,对吧? 接下来就是和初中一样,我们得把它放在一个直角三角形里面,所以我过这个 p 点做了个垂线下来,那么就能围成一个直角三角形,那么这个 r 法的三角形呢,就是它的对边比上这个斜边,也就是这个 y 比上 r, 然后它的 cosine 呢,就是它的零边比上这个斜边,也就是这个 x 比上这个 r, 那 么它的 tenon 呢,就是它的对边比上它的零边吧,也就是 y 比上 x。 这个是第一项线角,它跟我们初中学的是很像的啊,然后第二项线角呢,它就跟初中不太一样了,我们这个是使边旋转之后得到的这个中边交汇这个点 r 法,它的 sign 呢,就是等于这个 p 点的 y 比上这个 r, 所以 sine r 法,它还是 y 比上 r, 那 么它这个角的 cosine 呢,就是等于它的 x 比上这个 r, 这个是它的 x, 这个是它的 r, 也就是 cosine 还是这个数。那么 tangent 也是同样的道理, 你的第三和第四象限也是这样去做。所以我们以后见到三的函数呢,就是把它放在一个圆里面,然后记这个中边和这个圆的交点为这个 p, 这个角的 sign 值呢,就是这个 p 点的 y 比上这个半径 r, 就是 y 比 r, 这个角的 cosine 呢,就是这个 p 点的 x 比上这个半径,也就是 x 比上 r, 那 么它的顶点呢,就是 y 比上 r, 就是 这样啊, 不管是哪个象限的角,我们这个半径 r 呢,他都能用勾股定律算出来吧,就是根号下 s 方加 y 方,对不对?所以这个半径肯定永远是个正数啊, 既然半径永远是个正数,那么我们这个角的三角值呢,他就全由这个 y 来决定了,就是这个 y 决定了这个三角 y 也是正的,所以在第一象限和第二象限,他的三角值都是正的, 那么第三象限和第四象限,它的 y 是 负的吧,所以第三和第四象限它的三元值就是负的,就这么来的啊,所以我们看后面这里,这两个就是正的,然后下面两个就负的, 一二是正的,三四是负的,这是三元值。然后我们再来看这个,那么你这个 r 还是个正数,你这个 cosine 值的正负就全由这个 x 来决定吧。所以呢,我们看一下这个图, 你的这个第一项线和这个第四项线,它的 x 是 正的吧,所以这两个是正的。那么这两个这两个啊就是负的吧?负的,负的, ok, 所以呢, 它的 cosine 值呢,全由那个焦点的 x 决定,那么 x 在 一和四是正的,所以 cosine 值是正的, x 在 二和三是负的,所以这两个就是负的啊。 然后我们再看你这个 tangent 是 不是由 y 和 x 共同决定,那你想一下,第一项线 x, y 是 不是都正的,所以比出来那个 tangent 值就是正的。 然后第二项线是不是 y 是 正的, x 是 负的,所以它就是负的。第三项线是不是 x 是 负的, y 也是负的,负负得正。第四项线 x 是 正的, y 是 负的,所以比出来这个直角负的, ok, 这些要记住后面有用。 我们再看到这里问大家一个问题,我这个圆的半径,它的大小就是我这个圆大一点还是小一点,它会不会影响我这个角的三角函数值?会不会影响它的三 cosine? 你 想一下, 答案是不会啊,前面讲这个地方的时候就已经讲过了,你这些 sine 值 cosine 值,它的大小只跟这个角的大小有关系,跟这些边的长短是没有关系的。我可以画一个大圆啊,我们画一个大圆, 你看,那么这里是不是有一根中边,它延长出来,就这个红色的边它延长出来啊, 这个红色的边延长出来,到这里,这个焦点是那个 p 啊,那么他做了个垂线下来,那你说这个三角形和这个小的三角形,他是不是相似的呀?他们两个角是一样的吗? 那相似的他的这个对边比斜边,他比出来这个比值肯定是一样的吧。所以这个圆的大小,他并不影响我们研究他的三角函数值啊。 那既然不影响,我肯定要消除掉这个半径吧,对不对?所以我们就只研究单位圆,我让这个半径是等于一,那么这个 sign 呢?它就会变成了 y, cosine 呢?它就会变成 x, 天然还是 y b x, 所以 这是书上写的这个东西啊,你看,正弦就是 sign, 余弦就是 cosine, 然后正弦呢,就是这个 y 比上这个 x, 它就是 ten。 我 们这个 sin 和这个 cosine 呢,它都是没有限制的,也就是它直接等于 y, 直接等于 x, 但这个 y 比上 x 呢?它是不是要求分母不能是零啊?所以这里要求 x 不 能是零。 x 是 这个 p 点的横坐标啊, x 等于零,也就是 p 点落在 y 轴上面,也就是这个点和这个点吧。是不是当这个角的中边落在 y 轴上面的时候,这个 p 点它就落在 y 轴了吗?是不是二分之派加上 k 派? 这是第一次再加 k 派, k 派, k 派, k 派是不是一直落在 y 轴上面?所以当这个算法等于二分之派加 k 派的时候,这个贪婪他是没有意义的。 那么我们就将这个正弦与弦正切,统称为三角函数。正弦函数呢,就是 y 等于三 x, 这个 s 是 没有限制的, y 等于 cos x, x 也是没有限制的。 ten x 的 时候呢,我们要求这个 s, s 就是 这个时候的 r 法啊, s 是 那个角, 这个阿法呢,它就不等于二分之派加 k 派, k 是 属于这个。 ok, 我 们来看一下题目啊,先看一下这个利益,求这个三分之五派的正弦与弦正切,那就是先画一个圆出来, 这个角是三分之五派,它就比二派要少一点,所以这个角大概是位于这里啊, 整一圈是二派,三分之五派就比二派要少了个三分之派吧,说明这个角是三分之派。我们画的肯定是单位圆,所以这个蓝色的线是等于一,这个点的坐标我们就可以求了,我们往这里做个垂线下来, 三分之派呢,是个六十度,说明这边是个三十度,三十度所对的直角边是等于斜边的一半,所以这个是二分之一,那么这一根呢,就是二分之,刚好三吧, 二分之根号三,所以这个 p 点的坐标就有了啊,它的坐标就是二分之一,然后这个是 y 是 负的啊,是负的二分之根号三,这样就求出来了,那么它的 sine 值 sine 三分之五 pi, 它就会等于它的 y 吧,对不对?这些都有啊,就等于 y, 然后 cosine 就 等于 x, 等于 y 等于 x, 我 们来看一下,就等于它的 y 就是 负的二分之一,根号三,然后它的 cosine 就等于它的 x, 它的 x 是 二分之一,它的 tenon 就 等于 y, 比上 x 也就会等于负的二分之一,根号三,比上这个二分之一负根号三。好,那么这个例二我们就不看了,这个已经讲过了, 在这里都有啊,这个 r 都有啊,我们来看下这个啊。同样的,我们就是画一个单位圆, 然后找出它的中边,菱角的中边就位于这里,所以这个点就是 p 点,它是 e, 零。因为是单位圆,所以它的 sine 就 等于它的 y 等于零,它的 cosine 就 等于它的 x, 它的 x 是 一,它的 tangent 呢, 就会等于 y 比乘 x, y 是 零嘛,所以就是零。然后再看第二个二分之 pi, 那 就是位于这里了,这个角是九十度嘛,这个地方是二分之 pi, 所以 这个点的 p 呢?它是零一,那么 sine 的 二分之 pi, 它就等于它的 y 就是 一 cosine 二分之 pi 就 等于它的 x, 它的 x 是 零,然后 tangent 的 二分之 pi, 你 可以发现 y 比乘 x, x 是 零,所以它这个时候是不存在的啊。 好,我们继续看 pi 在 哪里? pi 应该是这里吧,所以这个点是 p, pi 是 一百八啊,所以这个点是负一零。 那么 sine 的 pi 就 等于它的 y 等于零。 cosine 的 pi 呢?就等于它的 x 等于负一。 tensin 的 pi 呢?就等于 y 比上 x, 所以 等于零。然后二分之三 pi 应该是位于这个地方啊,我用黑笔应该是位于这个地方,这个零是 p, 那 么它的坐标是零负一,所以 sine 的 二分之三 pi, 它是等于它的 y 等于负一。 cosine 的 二分之三 pi, 它是等于它的 x 等于零。 tangent 的 二分之三 pi, 它是等于 y 比上 x, 它是不存在,因为 x 等于零。 ok, 我 们再看一下这边这个第三题, 这个 c 塔角的中间过这个点 p 嘛,那么很明显它画出来的圆的半径肯定是很大的, 是不是?这是负十二,然后这地方是五吧,位于这里,这一根半径他就是十三啊,所以这个角他是不是有可能是长这个样子的,只绕了一段吧,那他是不是还有可能是这样子的,再绕了一圈过来吧。所以他是怎么样 原本的这个 c 塔,原本的这个 c 塔再加上了一个二 k 牌吧,对不对?因为他不止可以绕一圈,对吧?一直转一直转一直转, 所以你发现什么中边相同的那些角,他的三角函数值都是一样大的,因为他只取决于这个点,这个点就是那个 p 点取决于他的 x, y 负十二和五百。所以我们来算一下 sin 的 theta, 它应该等于 y 比上 r, 所以 它会等于五比上十三吧, r 就是 那个半径,也就是这根十三啊,估估数。然后 cosine 的 theta, 它会等于 x 比上 r, x 是 负十二比上这个十三,那么 tenon, 他就会等于 y 比上 x, 他 会等于五比上负十二,也就是负的十二分之五。 ok, 通过这个题目的讲解,我们也就可以知道下面这些东西, 因为阿法加上一个二 k 派吗?他们中间都是相同的,所以他的三角函数的值肯定都是相同的。我们再来看一下最后两个公式, 就这里我们刚说过,我们是放在单位圆里面去研究的。然后这个点是 p, 它是 x, y, 那 么连接它这根线是半径,那么这个半径 r, 它是单位圆,它等于一,所以它会等于根号下 s 方加 y 方吧,对不对?那么我们的 x, 它是等于 cosine 的 阿尔法, y 是 等于 sine 的 阿尔法。你把这两个带到里面去,你就可以知道 sign alpha 的 平方加上 cosine alpha 的 平方,开个根号,它会等于一两边平方,你就可以得到 sine 的 alpha 的 平方加上 cosine alpha 的 平方会等于一,所以就能得到这个公式。然后下面这个东西呢,我们知道 tangent 的 alpha, 它是等于 y 比上 x 的 嘛, y 不 就是 sine alpha 吗? x 就是 cosine alpha 就是 cosine alpha, 所以 它就能得到下面这个公式。 ok, 我 们来看一下这个例六,已知这个 sine, 求这个 cosine 和 tangent, 我 们不是有这个公式吗?所以我们就知道 cosine 的 alpha 的 平方,它会等于一减去 sine alpha 的 平方,他会等于一减去这个平方就是二十五分之九,所以他会等于二十五分之十六,那么他开根号应该取正负吧,所以我们就能得到 cosine 的 alpha 等于正的开根号就是五分之四,然后或 cosine 的 alpha 等于负的五分之四吧。那么这个时候是两个情况,我们要确定一下它是正的还是负的,或者说两个都可以,你就看一下这个 cosine alpha, 它是那个 y 嘛? y 在 什么时候取负, 这是正的,这是正的,这是负的,这是负的,说明它是三四象限。那么三四象限,这个这个 cosine 呢?它不是都是 x 吗? x 它是。 呃,这里是正的,这里是正负的,负的,负的,所以它是不是在三四象限可正可负啊?说明这两个值都有可能是答案啊。所以呢,当第一个情况, 当 cosine alpha 它等于这个五分之四的时候,那么这个 tangent alpha, 它会等于 sine alpha 比上 cosine alpha, 就 这公式啊,所以它会等于负的五分之三,比上 五分之四,也就是等于负的四分之三。第二种情况,当 cosine alpha 等于负的五分之四的时候, 天然的 alpha, 同样的,你用这个去算,算出来就是差一个符号,也就是四分之三,就这里 如果他是负的,那么 ten 人算出来就是正的,你看这里是负的, ten 人算出来是正的负,负的正嘛,然后如果他是正的,就上面这个算出来, ten 人就是负的,跟我们这算的是一样的啊。好,那么这是一种做法,我们还可以讲一下另外一种做法啊,我们再擦掉讲一下另外一种做法。 讲另外一种做法之前呢,我们得先看一下前面,也就是讲这里的时候啊,我们得把高中的这个定义和初中的这个定义给它联系起来。怎么联系呢?就是我们知道高中就是过这个中边与这个圆的这个焦点做个垂线下来吗?你就能得到这样的一个三角形。那么 你跟初中联系起来呢,就是造出了这个三角形之后呢,你找到这个圆点的这个角啊,圆点出发的这个角啊,那么这个角呢,他的这个三角函数值呢?就是我们这个点的中边的三角函数值了。 第一个他就完全跟初中是一样的,刚已经讲过了,我们直接看第二个啊,那么你就看你过这个中边的点,照了一个直角三角形出来之后呢,你就找到圆点出发的这个角,就这个地方啊,那么他的三角函数值,你看跟这个一不一样,你看这个角,我记住这个 叉啊,就是绿色的这个地方,那么它的 sign 是 不就是 y 比上 r? 是 不是对边比斜边?是 y 比上 r 一 样的吗?它的 cosine 呢?是不是这个 x 比上这个 r? 是 不是 x 比上 r, 那 么它的这个 呃摊子呢?是不是这个 y 比上这个 x, y 比上 x 是 一样的吗?只不过这里面的 y 和 x 也都是带符号的啊,你看你这个时候这个 x 是 个负数吗?对不对?所以它也是带符号的啊, 跟初中就是还是有点细微的差别,带符号要注意,我们看一下这个第三象限,那么这个时候呢,你就过这个点,照了一个直角三角形出来之后呢,你就找到圆点出发的这个 就这个角啊,还是用绿色写,就这个角吧,是不是圆点出发,是吧?然后他,你看他的 sign 是 不就是这个 y 比上这个 r, 然后他的 cosine 呢?是不就是这个 x 比上这个 r, 他的 tenon 呢?是不就是这个 y? y 比上这个 x, 对 吧?都是一样的,跟这上面一样的。那么第四个图我就不啰嗦了啊,反正都是一样的。 好,那么这样你就跟初中联系到一块去了,那么这样做有什么好处呢?也就是我们不用管这个角的大小, 不用去管,说他多大,你就直接假设他是个锐角就行了,你看我们就在画 假设这个角就是阿法,就我也不管这个阿法是多大,我就假设他的这个角就行了,好,然后呢,他的他不就是这个对边吗?是三,然后这个斜边是五百,你看三比五,这个时候我们符号先站起来不看他,站起来不看他,所以三比五,那么根据勾股定律,三四五我们就求出来了, 所以他这个 cosine 的 阿法,你看 cosine 这个阿法是不就是这个零边比斜边啊,所以他会等于这个五分之四吧,那五分之四你这样确定的是它的值吧?我们再来根据这个象限确定它的符号,你看一下,因为这个 嗯三,它是小零的吗?所以它肯定是三四象限,那么你就一想,三四象限这个 cosine 是 怎么样的呀?是不是 扣三,这里是正的,这里是负的吧,所以他这个值可正可负,所以他应该是两个就扣三阿法等于负的五分之四,扣三阿法等于正的五分之四吧。然后下面就跟第一种做法是一样的了,这种方法也是通用的,你也可以用。我们再来看一下这个题啊, 看一下这个题啊。第一题,我们用第一种方法先来做啊,就是 sin 的 alpha 的 平方,它等于一减去 cosine, alpha 的 平方,它会等于一减去二十五分之十六,所以它等于二十五分之九。开平方出来, sin 应该等于 呃正负的五分之三,那么他自己已经跟你说了,他是第三象限,第三象限 sin 只能取负的,哼,所以 sin 的 alpha 就 等于 五分之三啊,负的加个符号,那么 ten 呢?就等于三 比上这个扣三,所以它等于负的五分之三,比上这个呃负的五分之四,负的五分之四,所以负负得正,它等于四分之三。好,这是第一种做法,就是用了这个公式啊,那么我们用刚讲的那第二种做法, 你不用去管这个角,它多大,你就当锐角就行了啊。好, 所以这个角是那个 alpha, 那 么它是 cosine 嘛?你也不用先不看这个符号啊,它是四比五,说明它的零边是四,斜边是五,那么这个就自然是三了,因为它是垂直的勾股数,然后我们要求它的 sine alpha, 它是不就是这个三比上这个五啊, 所以它其实就是五分之三。那 tenon 你 也可以顺便求吗? tenon alpha 是 不就是三比上四啊?所以就是三比上四,然后再来确定符号吗?符号的话呢,这个是第三象限,就是你前面讲的这个,你要熟啊,就这些,你要熟 立马就反应的出来第三象限,这个,呃,肯定是负的,然后这个填减他是正的啊,所以这个答案是负的五分之三,这个是四分之三。 ok, 我 们再来看一下下面这个化简啊,就这个,这个你肯定用公式嘛, cosine 的 c, 它乘以这个天然 c, 它是不等于 cosine c, 它,所以它会等于 cosine c, 它 第一个题,第一个题花钱就是三 c 的, 然后第二个,嗯,这个一我不是可以改一下吗?对吧? 一等于这个东西吗?等量代换啊,把它改一下,它就等于两倍的 cosine alpha 的 平方减去 cosine alpha 平方加上 cosine alpha 平方,比上一一就是 sin 阿法平方加上 cosine 阿法平方减去两倍的 sine 阿法平方,所以它会等于,呃,这个跟这个干掉一个,所以是 cosine 阿法平方加上不对, cosine 阿法平方减去 sin 阿法平方再比上下面的话呢,就是这个跟这个干掉一个,所以它是 cosine 阿法平方减去 cosine 阿法平方,所以它等于一,这个数是等于一。 好,我们再看最后一个啊,最后一个,这个直接重开吧。直接重开啊,它就是 cosine 阿法平方,再加上 tenan alpha 平方,乘以 cosine alpha 平方,然后换一下。 这个是 cosine alpha 平方,下面是 cosine alpha 平方,再乘个 cosine alpha 平方,然后这两个约分 他会等于 cosine alpha 平方加上 sine alpha 平方,等于一啊。好,所以这个数是等于一,然后再看最后一个。哼,这个第五个。求证这东西。这东西一看像啥? 很像完全平方公式,会不会是不是很像?那你看咋弄啊?他像完全平方公式啊,因为这里是个四,然后这里是他的,他的一半吗?对吧?次数比他低一半,然后这个又是个平方,但是我希望这个东西是个四次吧, 所以我怎么样给他搞成四次?就是我希望照一个完全平方公式出来啊,所以我怎么弄?试一下塞阿法的四次 再加上三阿法平方。勾三阿法平方,再加上勾三阿法平方。我给他乘个一吧,乘个一,乘个一就是谁 乘个一就是三阿法平方,加勾三阿法平方,等于,对吧?没问题,然后给他打开就是三阿法四次。 找敲啊。加上 cosine alpha 平方乘以 sine alpha 平方,再加上 cosine alpha, 这是两次,两次就四次,四次等于一。你发现这个东西就是啥?这个和这个 啊,他就可以根据中间这个啊,这个,这个就两倍了吗?整理一下,就这样啊。三阿法四次乘以两倍的三阿法平方,加上。哎,不对, 是乘以 cosine alpha 平方,加上 cosine alpha 四次等于一,你发现这是啥?它这里是加的啊,它就是完全平方公式 cosine alpha 平方,加上 cosine alpha 平方再平方等于一, 你发现是不是?是不是这个东西完全平衡公式打开就等于上面这个没有算错啊,所以这里面是等于一吗?是一的平方,它还等于一吗?那我就正完了啊。好,我们就讲到这里。
28讲数学的吴老师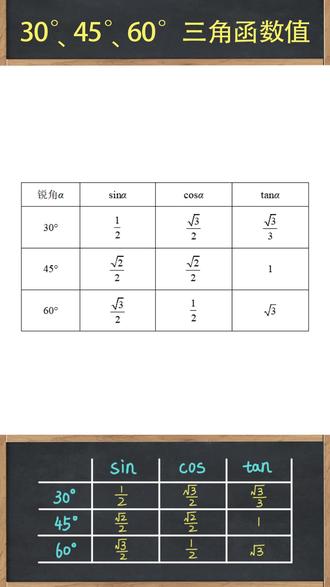 05:54查看AI文稿AI文稿
05:54查看AI文稿AI文稿同学们好,我是杨老师,这个视频呢,来帮助大家记忆一下啊,三十度角,四十五度角,六十度角,他们的三角函数值, 大家看这个表格,那这个表格是要求每个同学都必须熟记于心,那如果你考试的过程中啊,忘记了 啊,或者说你记的不准确,那该怎么办啊?今天我就教大家如何通过计算来自己写出这些特殊角的三角函数值啊。首先我们得知道正弦值,余弦值还有正切值怎么去算? 那正弦值指的是 sine, 它等于角相对的直角边比上一个斜边, 那简单来说就是对比斜。那余弦值是 cosine, 指的是角相邻的直角边,比上一个斜边,简单来说就是零比斜。 正切值指的是 tangent, 角相对的直角边比上一个角相邻的直角边,那简单来说就是对比邻啊。大家一定要把这个 对应的比例关系要记准确。嗯,如果谁把这个比例关系,就是谁比谁没有记准确。之后,我们再学后面的方法啊。 大家可以把视频先暂停一下,去梳理一下 sign, cause, sign, 还有 tagent, 到底是谁比谁啊?如果你确定啊,自己对这个比例关系谁比谁很熟悉没有问题,那我们继续往后学。 嗯,首先我们学习一下三十度角和六十度角,它们的三角函数值怎么去算。我们先画一个直角三角形,让这个角是三十度,那另一个锐角就是六十,那我们令三十度角所对的直角边是一, 那我们根据直角三角形中三十度角所对的直角边是斜边的一半,我们算出斜边就是二,然后再利用勾股定律算一算另一条直角边是多少根号下二方减一方等于根号三。 好了,三边的值有了,我们算一算,三 in 三十度就是三十度角,对的直角边,比上一个斜边,那就是一,比个二就是二分之一。那 cosine 三十度, 那等于三十度角,相邻的直角边,比上一个斜边,那就是根号三。比二就是二分之根号三。 最后 trigon 三十度等于三十度角,相对的直角边,比上一个三十度角 相邻的直角边,那就是一。比根号三,那就是根号三分之一。最后我们一化简分子分母同时乘以根号三,那就是三分之根号三。好了,这是三十度角的 sine 值,还有 trigon 的 值。 那接着我们另一个角是六十度,那我们算一下 sine 六十度是六十度角,相对的直角边,比上一个斜边,那就是根号三,比个二,那就是二分之根号三。 接着 cosine 六十度等于六十度角,相邻的直角边,比上一个斜边,那就是一,比上一个二,那就是二分之一。 那最后胎震的六十度等于六十度角,相对的直角边,比上一个六十度角相邻的直角边,那就是根号三。比个一就是根号三啊。好了,这就是 呃,六十度角的三根 cosine 值,还有 time 值。那继续我们来学习一下四十五度角的三角函数值,那我们画一个含四十五度角的直角三角形, 那很明显两个锐角都是四十五度,那它就是一个等腰直角三角形。我们令两条直角边都是一。用勾股定律算一下,斜边就是根号,下一方加一方等于根号二, 那 sine 四十五度等于四十五度角相对的直角边比上一个斜边,那就是一比根号二。最后我们一化简,分子分母同时乘以根号二,结果是二分之根号二。 cosine 四十五度等于四十五度角相邻的直角边比上一个斜边,它还是一比根号二。最后我们一化简是二分之根号二, 那我们发现不管是 sine 四十五度还是 cosine 四十五度,它们的值都是二分之根号二, 这个是比较特殊,好记一些。那最后 trigunt 四十五度就是四十五度角相对的直角边儿,比上一个四十五度角相邻的直角边儿,那都是一呀,那一比一等于几?等于一,所以 trigunt 四十五度等于一。 好了,这个是通过计算算出三十度角、六十度角以及四十五度角的三角函数值。那考试的时候如果你啊记得不准确或者不确定,那我们可以算一算。
17初中数学加油站 00:38查看AI文稿AI文稿
00:38查看AI文稿AI文稿意图秒记三角函数,画一个三十度和六十度的直角三角形,让短边为一, 其他两边就是二和根号三复制旋转拼接,这里就是直角,两直角边等边都是二,连接就是等腰。直角三角形斜边就是两倍。根号二复制延长就组成一个矩形,这两个角就分别是十五度和七十五度,这个边是根号三加一, 这个边是根号三减一。三角函数公式都知道了,代入就可以得到所有常用三角函数的值。
54数学小课堂 09:25查看AI文稿AI文稿
09:25查看AI文稿AI文稿三角函数刚学就懵,概念这块总结的抽象又绕,今天直接对准高考里三角函数概念的核心考点,从定义到关键细节,把这块地基打牢,后面学图像公式都能顺顺当当,快艾特你那还在迷糊的同桌,一起把概念吃透,不丢分。接下来继续带各位三角函数的部分, 那我们前面说完了,任意角啊,那在这里呢,我们知道了任意角和弧度制,那我现在既然角都可以 从负无穷到正无穷,可以随便加减一百八,随便加减三百六,到,而且能把一百八写成派,三百六写成二派,随意加减二派,加减二派之后呢,那这时候我们任意的角度,任意的弧度,哎,他用三角函数 怎么去表示,对吧?哎,那我们就来看啊,首先呢,我们还是啊,就是高一,我一直强调不要去背概念,没有意义啊,理解就行啊,所有东西都是在你以前的基础上由理解进发而得到的。那我们来看什么叫三角函数,咱先类比初中你学的,我们先讲初中三角函数的概念啊,锐角, 那这时候呢,你就会画一个角,这角画小一点,这是一锐角,你就画一锐角,三角形 啊,啊,直掉三角形,不好意思,直掉三角形其中一个顶点除以角,你会研究这个角 c 它,然后这角 c 它,你会发现,哎,如果对边是 a, 这边是 b, 这是 c, 那 你就说,哦,散 c, 它就等于 a 除以 c cosine c, 它呢 就等于 b 除以 c 它,那个 c, 它呢?就等于 a 除以 b, 对 吧?这事没错,而且这个事其实在高中会一直用,因为这个毕竟直观,而且是你从小根深蒂固的。那你看,为了好算,我可以怎么办?如果你让 c 等于一, 如果你令 c 得一,那这时候它是不是就会变成 b, 这还是 ab? 如果你令 c 等于一的话, 对吧?那你看,令 c 得一这件事有点像什么呀?有点像,我画一个圆,但我让半径等一。那各位看看,如果我把它变成一个任意角 来对比啊,这是咱们初中的,那咱到了高中之后呢?任意角,我们是不是就要画一个象限?这可能是你的象限,对吧?那我这时候呢,画个什么呢?还记得我们转圈吧,那就画一单位圆。 在相片里画一单位圆,那各位卡在单位圆中,我可不可以画一个角度?我如果想表示跟刚才一样的角 c, 它这个角 c, 它,我就画在这。 好,这就是我的角 c, 它跟刚才那个角是一样的。哎,哎,画的还正好,是吧?哎,这个画图 g 无的正好是一个角 c, 能看出这是一个角吧?哎,这是同一角。好, 好,现在你看啊,我在这个图里如果画三角函数,我这画的是个单位圆,这个点是一,就是 r 等于一的单位圆。好吧, 一是单位吗?什么叫单位圆?单位圆的意思呢?就是半径为一个单位长的圆,叫单位圆啊。单位长的意思好, r 得一吗?就是单位长。那这样画一个圆,你会发现在这里啊,我就可以把这三角形画出来, 哎,这就是我的三角形,然后你发现在这里呢,这条边 这个小,这个 a 就是 你的三,看出来了吧,如果你这个角叫做,我就管这角叫 x 吧。 啊,咱就不用 c 它了,毕竟咱得用变成函数嘛,函数自变量得是 x 啊,对吧?那我这就叫 x。 那 其实你发现,因为你边长 r 得一嘛,所以你这高度,它就是三,这就是三 x, 这个长度就是三 x, 那 底下这段长呢?它就是 cos。 哎,你看,在这个单位圆里,如果把一个点,这个点在单位圆上,它的对应的中边是 x, 中边做一条垂线,长度就是三, 然后横着这段就是扣三,是不是跟这段是 b, 扣三,这段是 a, 三是对应的,只要 c 得一,能理解吧。那我就把什么呢?我就把这个角放成我们刚才任意角的情况了,那在这种情况下,我是不是这条边就可以开始转了? 那什么叫这角?当你这条边转的时候,你会发现三和扣三就会有变化了。啊,三和扣三就会有变化了啊,三和扣三怎么变的?我们来看看啊。当你这转的时候,你看啊,我如果这个角转到这, 这时候谁是三和扣三啊?啊,注意啊,我画个颜色,我三都用黄笔画, 我黄色笔代表的是三,红色笔代表 q 三,我单画一个圆。好吧,现在我就要给它扩充到任意角度的三角函数了。当往这条边转的时候,如果你在这,那三是什么?我三用黄笔, 这条边就是三,反得一单位圆,那这条边就是 q 三,那我再转,当你这么转的时候,这条边就是三,这条边就是 q 三, 没问题吧?那我再转,转到数值九十度的时候,你看哪散哪扣散,哎,散就是这段,他还是散,你发现时候散得一,这时候散最大,这就是散,是不是这段啊?从这个点向挨着做垂线,我类比吗?那你发现扣散就变成一个点,扣散就是零了, 那我再转啊。哎,这点转到这,各位会发现,哪是散啊?这一段是散,而你扣散到这, 你看,你看,这是扣三,这是扣三。现在你扣三上,这我再接着转,我再划几个,别人就要编,编到这, 你的三呢?这段垂线,我把箭头往上划,因为它在上,然后你的扣三呢?是这段。 所以各位发现,在你的角度从零度转到一百八十度的过程里,当你转的时候,你的三角函数,这个点,你可以理解为向 a 轴的距离,这个就是散,他就一直在变化。哎,你横向的这个距离呢?他也在变化,那我让他转起来,你散和扣散就永远能找到一个对应的线, 对吧?那我如果再转,转到这,那你会发现这个时候这就是你的三,然后呢,你的红线还是往左的这个,这就是你的 cos, 同样,如果你转到这个位置呢?哎,这就是你的散,然后这是你的扣散。所以各位在你转的过程中,有没有发现叫做散和扣散啊?永远是一个是竖向的,一个是横向的,可以表示这就是任意角的三角函数。那我既然定义了这段是散,那你发现 我这两个点就得有所区别,这俩角毕竟不一样,对吧?这俩角一个在第二向前,一个在第三向前,那不一样,那我怎么区别?那就看,既然这个箭头如果往上划,就即为是三 x 大 于零为正。 如果你这个箭头往下划,我三 x, 那 就跟我坐标一样。我小学的时候不讲究负数学,一个长度距离都是正数,对吧?但你到了初中就学竖轴,竖轴要往右走是正的,那反过来反着走往左是不是就叫负的? 那到了高中一样,你看三角还是我们原来锐角三角二都是正,但现在呢?哎,你往上划, 因为三角函数正弦就是上下,那你肯定定义往上为正吧?外轴正方向往上为正,那往下是不是即为负?所以往下的三角函数正弦就是负的。咱再看 cos, cos 是 左右的, 对吧?那既然 q 三是左右的,那我肯定往右这段儿这些的 q 三,这些的 q 三叫做 q 三, x 大 于零为正,那你往左的,我肯定定你为负啊。哎,往左的 q 三 x 是 不是负的了?哎,这个就是三角函数 任意角的情况,就是增加了正负,就可以在这个点在圆上转圈的时候看它的坐标记。所以各位有没有发现,单位圆上一个点,看着单位圆上一个点,它的横坐标是谁?它的横坐标就是 q 三 x, 纵坐标就是三 x 啊。所以各位要知道,其实一个任意角的三角函数就是单位圆上角度为 x 的 点,那它的坐标就是 cos x。 逗号 cos, 所以 任意角的三角函数,你就明白,这个点的横坐标就是 cos x, 纵坐标就是 cos x。 而 r 又等于一勾股定里就永远有 cos x 加 cos 方 x, 永远得意这事永远成立。这角是啥都成立,零度九十度,正的负的一百八三百六,一千零八十度,这全成立。哎,这就是用勾股定力关系。初中的直角锐角三角形推你的这个这个这个正余弦其实是一样的。
69胡源高中数学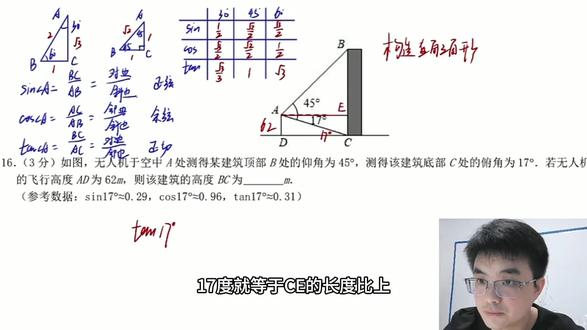 09:45查看AI文稿AI文稿
09:45查看AI文稿AI文稿今天我们用这个视频来学习一下锐角三角函数这个知识点。先看一下定义,在一个直角三角形中,角 a 是 等于 bc 比上 ab, 也就是说角 a 的 对边比上斜边,这个叫做正弦 cosine, 角 a 等于 ac, 比上 ab 是 邻边比上斜边称之为余弦。单阵的角 a 等于对边比上邻边, ac 比上 bc, 对 于角 a 来说, bc 是 对边, ac 是 邻边, ab 是 斜边。 这个等大家熟悉了之后,是非常简单的,也就是我们课本上的定义。再次给大家罗列一下,单阵的角 a 是 对边比上 零变,这个我们称之为正切函数,这是我们要明确三角函数的定义。还有一个需要掌握点,就是特殊的三角函数的值要把它给背下来,比如说这是三十度,这个是六十度。 我们再画一个,比如说这是 abc, 这两个角都是四十五度,角 c 是 九十度,那我们来列一个简单的表格,大家来记忆一下。 三 cosine 分 别三十度、四十五度、六十度,这也是我们初中数学最后一章的内容了,大家学完这一章之后,我们整个初中数学部分就学习结束了,就可以转入到正式的复习中。根据图形来记忆, bc 设为一分, ac 是 根号三分, ab 是 两分, bc 是 一分, ab 是 根号二分,所以说三十度,大家记一下,这是二分之一。 当然同样的考三英六十度是零边,比上斜边也是二分之一,三英六十度是二分之根号三,考三英三十度也是二分之根号三。在这里三英四十五度和考三英四十五度都是二分之根号二。 最后一个 tangent 分 别是三分之根三一和根号三,大家掌握好,我们来学习一下这一道第十六题的填空题,这是大概是一九年的题目, 而且呃,我们可以确认一下,这个题是非常具有地区特征的,具有我们这个徐州市特征的,当时这个无人机恰好就是落在了市中心的锦绣名都商业楼附近, 然后测出来的这个 bc 的 高度就是刚刚建成的苏宁广场的高度,大致是这样子的,当然并不是准确高度。好,来看一下题目吧, a d 的 长度是六十二,这个信息也是老师开会的时候给我们提到的一个信息,十七度,那下面这个角也是十七度, a d 的 高度是六十二, b 处的阳角是四十五度,阳角我们确定一下,就是 ab 与水平面的夹角是四十五度。知道这些信息之后,求建筑 bc 的 高度, 我们就掌握三角函数的一个做题方法就可以了,就是一句话,构造直角三角形,不管题目类型是什么样子的,但是我们做题的原则就是这样子,所以说我们从 a 点直接向右做一条垂线,比如说这个点是 e 点好,那么 tangent, 十七度 就等于 c, e 的 长度比上 a e 的 长度, a d 是 六十二,比上 a e 的 长度等于题目中给到我们这个零点。三一,我们可以很轻松的算出 a e 就是 两百,然后因为这里这个角 b a e 是 四十五度,这个角也是四十五度,所以说 a e 和 b e 是 相等的, 那么 a e 等于 b, e 是 两百,所以说 bc 的 长度就是二百六十二。 这一年三角函数并没有考到大题,而是很简单放在一个十六题的这个位置。好,这个咱看一下它是不是属于我们一个现实的情况,我去搜了一下啊。大家可以看到这个徐州市苏宁广场 a 塔楼的高度是二百六十六米,是大致相同的, 这也是具有一个地区特征的题目,这个题目当然了也是非常简单,我们来看看下一题啊,这是一道期末考试的题, 我在此写一下。这一年的期末考试特别特殊,他把三角函数放到了最后一题,而且与学生的这个实际的学习生活非常贴切。是这样的,一个四十五度的直角三角板,和这样子一个三十度、六十度、九十度的直角三角板放到了一起的一个 问题,我们来读一下啊,把一个三角板拼在一起,则 a、 b、 d 等于七十五度,这个没有问题,四十五加上三十是七十五度。好,我们标出它这个角是七十五度, a、 c 是 六,那当然了 a、 b 也是六,直接去求三七十五度的值。 这个题目出的也是特别的好,得分率当时是并不高的,看着简单,而且我们待会讲解完之后,大家也会发现这个计算非常简单,但是在当时这个上学期九年级期末考试的时候,这个计算很多同学是没有拿到全分的,我们来一起分析一下题目 既然求的是三一七十五度,我在此讲一个错误的做法,因为当时有很多这个想去考创培,就是一中创培班的同学, 他是提前学了一个高一的内容,有这样一个公式,三英阿尔法加 betta 等于三英阿尔法 cosine betta 加上 cosine 阿尔法 cosine betta。 也就是说 cosine 阿尔法加 betta 等于三, cosine 加上 cosine。 这个方法直接三英三十度加上四十五度, 直接代数就可以得到最终结果了,我们来看一下啊,先看一下最终结果是多少吧,但是我给大家要说明的是,这样做是只给答案分,因为你没有用到我们初中的这个几何知识点。三 a 三十度加上四十五度二分之一, cos 四十五度二分之根号 加上 cos 三十度是二分之根三三 a 四十五度是二分之根二,化简得到结果是四分之根二加上根六。 如果说这个题这样做的话,都没有去学这些三角函数的必要了,我们本意还是通过这个几何来证明。我们再次说明这个方法是不能用的啊,你上高中之后可以用。好,先来分析一下角度, 四十五度标出来,四十五度标出来。既然要求三一七十五度,我们要找的是对边比上斜边,观察一下这个七十五度,对边是没有的, 根本就没有对边,但是斜边有,斜边是 b、 d。 好, 我们来看一下斜边 b、 d 的 长度,咱先给它求一下,因为 ab 等于 ac 等于六,所以 bc, 这里我简单写下,是六倍根号二。 好,这个是六倍根号二。题目中我们看到在三角形 d、 c、 b 中,角 d、 b、 c 等于三十度角 d、 c、 b 是 等于九十度的, 所以说我们用 tangent 角 d、 b、 c 等于对边 d、 c 比上邻边 c、 b, 也就是六倍根号二,我们简单的直接写 数字吧, dc 比上六倍根号二,这个结果是等于三分之根三,所以说 dc 的 结果就等于六倍根号六除以三,结果就是二倍的根号六, dc 就 说是二倍根号六,所以 b、 d 是 等于两倍的 cd 是 四倍的根号六。这里我们也标一下这个是四倍的根号六。 现在斜边已经搞定了,我们需要去找这个七十五度对边,所以说很明显我们要去做这样一条垂线。第一,这也验证了我刚刚写过的这个问题,是构造直角三角形,我们继续讲构造直角三角形,接下来我要去求第一的长度, 第一的长度怎么求?刚刚我表示出来了,这个角是四十五度,这个角是四十五度,所以说在此我们只需要这样做一条垂线,就可以确定这个角也是四十五度啊。我来标一下做 c、 f 垂直于第一得角 d, c、 f 等于四十五度, 因为 c、 d 等于二倍的根号六,所以说 cf 等于二倍的根号六,除以根号二。在这里我的用,我用的是比例关系来做的,他们的比例关系是一比一比根号二。所以当 cf 和 df 求出来了之后,我们就可以写出 d、 e 的 长度了, d 的 长度就是二倍的根号三,再加上 e、 f, 当然了在这里 e、 f 是 等于 a、 c 的,是二倍的根号三,加上六。好的,所以说三七十五度就是等于二倍的根号三,加上六,再除以四倍的根号六。 最后一步计算就是分子分母同乘根号六,我们化简一下,分母位置是二十四,分子位置就是六倍的根号二,加上六倍的根号六。我们化简出来得到的结果就是四分之根二加上根六。 好,这样的话我们这个题目就讲解完毕了,再来对照一下这个答案,跟这个答案是一模一样的啊, 还是那句话,当时是有不少学生是为了去考这个一中的创培班,所以说提前学了这个高一的三角函数的内容,但是如果说你直接用到这个期末考场上来的话,这个是不给分的,所以说我们还是要建立这个一个几何的方法, 在此可以多啰嗦两句。有些同学或者家长可能问,为什么这个方法不给分,这很简单,一个教育公平的问题。如果说高中的方法你都能用到初三的这个知识点上来的话,那可以说又加具了这种学习的内卷。同学们学习初三内容已经很辛苦了,你再让他去提前学这个高一的内容, 当然力所能及的同学你可以去学啊,但是我们考试包括中考,你还是要在这个考纲允许的范围内啊。今天我们就把这个三角函数知识点用两道题目给大家呃,串一下大家,欢迎关注我一下,我还会继续更新。
18数学精选题分享 06:22查看AI文稿AI文稿
06:22查看AI文稿AI文稿数学只能考五六十分你就绝望了吗?高考不到两百天的时间你就放弃了吗?我告诉你,一百分根本不是梦,难点不在于题目,而在于你的方法,是没有人给你指那条最有效的路。别怕,从今天起跟我走,我会把一百分的考点拆解了,揉碎了喂到你的嘴里,带你梳理必考模块,告诉你哪些分是必 须拿,哪些核心考点投入时间短,掌握难度低,但分值可不低,你只管跟着走,一百分稳了 你。就像我们的三角函数,包括减三角形这个模块相对来说它就非常的弱智,我希望你呢,通过我们的这个讲解,彻底搞定这个模块,基础再差,花上两天的时间就能够搞定这两模块,高考分子大概能够占到十七到二十二分,性价比极高。第一个就是公式, 你像公式的话,我们这一招说实话真的是比较死板,你得知道我们这一招考的公式有什么公式?那公式这一类有多少公式呢?大概有十几类 啊,不要嫌多啊,他们都是环环相扣。你比如第一个就是同角之间的关系,同角关系就是肾方加坎,肾方等于贪念的,等于肾迷和肾。那这个地方常见的题型就是知一求二,什么肾啊?肾二法考肾二法,贪念的二法,知一求二,我们知道其中一个,就能求出第二个。 第二个考法就是我们特别喜欢构造队友式,那你可能得知道什么叫队友式。第三个考法,我们这个地方往往都是构造奇数式,这就是同角之间的关系, 第一类公式,第二类公式就是诱导公式,即变偶不变符号看阳线。即使你不会推导,你也背过了吧,都是现推的,不是背的啊,因为诱导公式有无数个,即变偶不变符号看阳线。第三类公式呢,就是核差公式,我们渗二帕加贝塔,考察二帕加贝塔,贪婪的二帕加贝塔,那么核差公式它立刻推出什么来呢?所以你不要看的多,真的都是环环相扣, 你只要会背和他公式,那么你就会背二倍角公式,二倍角公式由他推出,那你就会背三倍角公式啊。三倍角公式我们高考考的非常少,模拟题考的多一点,所以一百分以下可以不会,那你就会辅助角公式。辅助角公式无论高考还是模拟题,这是必考的辅助角公式,它是有什么的? 那你就会背计划和差和差化积。哎,你说我不会背啊,你不会背就不背呗,推倒不就完了吗?计划和差和差化积,这个是二零二五年考到的,这个地方也是非常非常重要的啊。当然二倍角公式会了,你降密公式就会了, 你就知道怎么降密了。降密公式,当然你会背二倍公式的话,你也就会背半角公式,因为我是你的两倍,你就是我的一半嘛,半角公式我们就能够。 当然这就是第三大类啊,当然这一下子就得有几个公式了,一类两类,三类四类,五类六类哈,这都是推导出来的。当然第四类公式你就会被万能公式,万能公式是我们权威高评分,特别喜欢 考。当然和差公式你还能推出什么来?推出来,正弦平方差,余弦平方差,而且我们课本上是有的。第五大类就是正切和等式,在三角形的 a 加贪婪, b 加贪婪, c 等于贪婪的 a 乘以贪婪。 这些公式都学的好,所以把这些公式看成一个网,每一个公式怎么推导出来的?那么高考必得五分 啊,当然可能会说,哎呦,这太难了,我会这么多东西才得五分。高考就是这样,他不能说我直接告诉你就必须考哪个公司,考哪道题啊,他没有那么准啊,你只能是一步一步的去准备,但是我觉得花上一个小时,两个小时的时间一定能够学明白。 第二类考图像,图像的考法就相对来说更加的失败了。第一个就是正弦型函数的各种图像变换, a 倍的 sin, omega 加 f 加上一个 b, 那 么 a 的 作用是什么呀?振幅什么 omega 呢?横坐标伸缩, f 呢?左右平移, b 呢?上下平移, 所以呢,这就是正弦型函数,包括什么平行变换,包括已知图像,求解析式,这些都要掌握。第二类就是求偶悖根的范围这种题,哎,这是全卷考的烂的题型了啊,我告诉你,在一个区间上啊,是单调的求偶悖根的范围,我告诉你,在一个区间上单调,在这个区间上有几个零点,有几个对称轴,有一个对称轴,一个零点等等 求偶性的范围,这些说白了都是挣钱一些函数的问题。然后呢,第三类就是什么呢?和函数结合在一起,比如里边有绝对值啊,里边有求导啊,里边有均值不等式,也就说综合型问题,就是不只是三角函数的问题,它里边有可能有绝对值函数这个地方也是我们考试的重中之重,比如二零一九年全国各地考 过的,特别喜欢考,这就图像。好来我们再说减三角形。减三角形它的考法我觉得更简单,结论很少。第一个就是会背,会正正弦定平面面积公式三公式, 那你得会背吧,正弦定律怎么背,余弦定律怎么背,面积公式怎么背?怎么推导出来的啊?那这这是第一步啊,我们考试的时候,这是百分之百考,如果考解答题的话,相对来说,它表示的值基本上是属于送分值十三分或者十五分啊。前三个解答题,第一问往往都是利用正弦定律、余弦定律来求值,第二问往往都是求最值,他和基本功是结合在。 所以第二个呢,就是你得知道我们常见的求最值的方法是什么?求最值的方法,这是综合题,他有可能是基本,不能是求对值,这是考频最高的,他也有可能是一角一函数。什么叫一角一函数呢?就是化成一个角,一个函数的形式,一角一函数求对值也是有可能,他还有可能是和二次函数结合在一起,求 对值里边涉及了二次函数,这都很正常的。第三个呢,偶尔高考目前为止我们见过模拟题,都见过,他里边和倒数结合在一起, 它里边是一个三次函数。高次函数求对值,我们很明显我们要求,所以我们这一张常见的求对值大概就是四。 如果再加上一个小题,他也有可能利用轨迹方程,利用轨迹,比如他的轨迹是个圆啊,这个减数型特别喜欢和圆记合在一起,比如它的轨迹是个椭圆来求对值,这也是很有可能的。第三种画法就是什么三角定力啊,什么角平行线定力啊等等, 就说白了就是和三线问题,什么中线问题啊,高线问题啊,然后角平分线问题啊,旋涡角机盘。就考那么多模拟题,可能会考的更深,但是高考你会那么多真的足够,因为他即使考压轴题,像今年新高考就要考的第十一题,多选压轴题,他不是说你多会多少拓展知识,他考的是你的能力, 你的信会先猜后正,先猜后正,他能够猜出来他是个直角三角形,你只要猜出来他是直角三角形就非常简单了。所以你就把我给你讲这些内容,花上两天的时间搞定,十七分到二十二分搞定,那么一百分好凑,真的好凑,所以大家不要灰心,慢慢学,你得知道高考怎么考,你得知道每一个章节大概有什么内容,这才对。
2599步学赵礼显数学










