四年级上册科技节几何图绘世界

孩子自己也能动手制作的立体几何图形，二十一种图形，有简到难系统编排，覆盖小学到初中几何全部需求，每张展开图均精准测量，确保粘贴边能完美贴合，孩子自己就能动手操作。电子版即打即用，省时省力 解决教学难点，让抽箱的几何思维看得见、摸得着、拼得成。

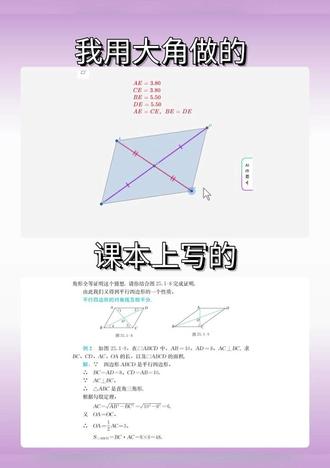
这是课本上写的，这是我用大角做的任意改变平行四边形的形状，对角线交点始终是两条对角线的中点。 结论，平行四边形对角线互相平分，做一个这样的图，只要三十秒，打开大角几何，画出平行四边形，画出对角线，标记出交点， 更改样式，突出重点，插入动态表达式来展示对角线的长度， 试试效果，完成。

你永远也考不过一个从小学四年级就开始学几何模型的孩子，因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了。 每个模型都有详细的图解、分析过程和总结，扫码还可以看动态演示图，让孩子们更好的理解图形变幻，培养孩子的几何思维，增强逻辑推理能力。每学会一个模型，就做一做配套练习册，对应的题型 学练结合，加强巩固，不会的扫码就能看视频讲解。跟着老师学习解析思路，吃透，模型快，给孩子也准备上一套！你永远也考不过一个从小学四年级就开始学几何模型的孩子， 因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了， 每个模型都有详细的图解分析过程和总结。你永远也考不过一个从小学四年级就开始学几何模型的孩子，因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了。 每个模型都有详细的图解、分析过程和总结，扫码还可以看动态演示图，让孩子们更好的理解图形变换，培养孩子的几何思维，增强逻辑推理能力。每学会一个模型，就做一做配套练习册，对应的集体 学练结合，加强巩固。不会的扫码就能看视频讲解。跟着老师学习解析思路，吃透，模型快，给孩子也准备上一套！你永远也考不过一个从小学四年级就开始学几何模型的孩子， 因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了。 每个模型都有详细的图解、分析过程和总结，你永远也考不过一个从小学四年级就开始学几何模型的孩子，因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了。 每个模型都有详细的图解、分析过程和总结。扫码还可以看动态演示图，让孩子们更好的理解图形变换，培养孩子的几何思维，增强逻辑推理能力。每学会一个模型，就做一做配套练习册，对应的集体 学练结合，加强巩固，不会的扫码就能看视频讲解，跟着老师学习解析思路，吃透模型快，给孩子也准备上一套。你永远也考不过一个从小学四年级就开始学几何模型的孩子， 因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了。 每个模型都有详细的图解、分析过程和总结，你永远也考不过一个从小学四年级就开始学几何模型的孩子，因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了。 每个模型都有详细的图解、分析过程和总结，扫码还可以看动态演示图，让孩子们更好的理解图形变换，培养孩子的几何思维，增强逻辑推理能力。每学会一个模型就做一做配套练习册，对应的集体 学练结合，加强巩固。不会的扫码就能看视频讲解。跟着老师学习解析思路，吃透模型快，给孩子也准备上一套，你永远也考不过一个从小学四年级就开始学几何模型的孩子， 因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了， 每个模型都有详细的图解、分析过程和总结。你永远也考不过一个从小学四年级就开始学几何模型的孩子，因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了！ 每个模型都有详细的图解、分析过程和总结。扫码还可以看动态演示图，让孩子们更好的理解图形变换，培养孩子的几何思维，增强逻辑推理能力。每学会一个模型就做一做配套练习册，对应的集体 学练结合，加强巩固，不会的扫码就能看视频讲解。跟着老师学习解析思路，吃透模型快，给孩子也准备上一套， 你永远也考不过一个从小学四年级就开始学几何模型的孩子，因为他们早早掌握了这九大模型的解析方法，具体不慌，思路清晰。如果你把这套书也吃透了，考试就不用慌了， 每个模型都有详细的图解、分析过程和总结。

你永远也干不过一个从四年级开始就学几何模型的孩子，因为他们清楚的知道，小学四到六年级的数学考来考去就这九大几何模型，把它们吃透，考试就好比翻书抄答案，这个是一半模型， 无论一点怎样变，阴影面积始终是长方形面积的一半，这是等高模型，又叫拉窗帘模型，同底等高，无论位置怎么改变，三角形面积都不会变。这些几何模型这本玩转几何都总结好了，并汇总了九大几何模型，像三角形就有等高模型、秒头模型、 沙漏模型、四边形就一半模型、蝴蝶模型、圆形就曲线模型，考试碰到哪种模型往上套，就能快速得出答案。而且孩子还可以亲手演示模型的推导过程，将复杂的几何知识变得可识化，孩子也更容易理解。学完后还有相关题型 是检测学习成果，利用好这套书，后面初中学几何会更轻松，快给孩子安排起来吧！你永远也干不过一个从四年级开始就学几何模型的孩子，因为他们清楚的知道，小学四到六年级的数学考来考去就这九大几何模型， 把它们吃透，考试就好比翻书抄答案，这个是一半模型，无论一点怎样变，阴影面积始终是长方形面积的一半，这是等高模型，又叫拉窗帘模型，同底等高，无论位置怎么改变， 三角形面积都不会变。这些几何模型这本玩转几何都总结好了，并汇总了九大几何模型，像三角形就有等高模型、鸟头模型、 沙漏模型，四边形就一半模型、蝴蝶模型，圆形就曲线模型，考试碰到哪种模型往上套就能快速得出答案，而且孩子还可以亲手演示模型的推导过程，将复杂的几何知识变得可识化，孩子也更容易理解。学完后还有相关题型 是检测学习成果。利用好这套书，后面初中学几何会更轻松，快给孩子安排起来吧！你永远也干不过一个从四年级开始就学几何模型的孩子，因为他们清楚的知道，小学四到六年级的数学考来考去就这九大几何模型， 把它们吃透，考试就好比翻书抄答案。这个是一半模型，无论一点怎样变，阴影面积始终是长方形面积的一半，这是等高模型，又叫拉窗帘模型，同底等高，无论位置怎么改变， 三角形面积都不会变。这些几何模型，这本玩转几何都总结好了，并汇总了九大几何模型，像三角形就有等高模型，鸟头模型、 沙漏模型、四边形就一半模型，蝴蝶模型、圆形就曲线模型，考试碰到哪种模型往上套就能快速得出答案，而且孩子还可以亲手演示模型的，往上套就能快速得出答案，而且孩子还可以亲手演示模型的推导过程，将复杂的几何知识变得可化，孩子也更容易理解。学完后还有相关题型， 及时检测学习成果。利用好这套书，后面初中学几何会更轻松。快给孩子安排起来吧！你永远也干不过一个从四年级开始就学几何模型的孩子，因为他们清楚的知道，小学四到六年级的数学考来考去就这九大几何模型，把它们吃透，考试就好比翻书抄答案。这个是一半模型， 无论一点怎样变，阴影面积始终是长方形面积的一半。这是等高模型，又叫拉窗帘模型，同底等高，无论位置怎么改变，三角形面积都不会变。这些几何模型，这本玩转几何都总结好了，并汇总了九大几何模型。像三角形就有等高模型，秒头模型、 沙漏模型、四边形就一半模型、蝴蝶模型，圆形就曲线模型。考试碰到哪种模型往上套，就能快速得出答案。而且孩子还可以亲手演示模型的推导过程，将复杂的几何知识变得可 直观，孩子也更容易理解。学完后还有相关题型，及时检测学习成果。利用好这套书，后面初中学几何会更轻松，快给孩子安排起来吧！

平行四边形的高你真的会画吗？像这个问题中，要让我们过 a 点做平行四边形的高，那 a 点是在这里，首先我们想到的就是过 a 点向 b、 c 这条边去做垂线，这是我们所做出来的高， 那只有这一条吗？如果只能画出这一条的话，说明对于平行四边形的高还不是特别理解。除了这一条之外，我们高的画法是什么呢？高的画法其实就是过一点做它对边的垂线，那点 a 的 对边可以是 bc， 同样它也可以是 c、 d， 所以 也可以再过 a 点做 c、 d 的 垂线，这也是它的一条高，所以过 a 点做它的高，一共是有两条，你学会了吗？关注我，学习更多数学思维方法。

本周四年级讲义，我们开始学习第八单元。首先往年这些东西都是我抄在黑板上，小朋友要抄挤黑板的，今年呢，我把它打印了出来，把书中有的没有的重点都罗列了一下啊，后面依然是这样的。然后有一些必考的一个操作题及找规律的一个方法， 会教大家一些算角的一个技巧，包括这个角度与钟表的一个联系。 好，下面这个稍微是难一点的关于第八单元的一个复习要点，这个是非常的密密麻麻，总结的一个内容都是边讲边做的一个内容。嗯，这边都是必考的关于一些角度的一个折叠 啊，这边是偏思维类型的，题目很多，还有一个作图，动手作图的一个常考题型。

立体结合题啊，我们就要学会画直观头啊，这个菱长为二十厘米的正方体，我们可以先把它画下来啊，这个他的前面一面，好，这上面一面，然后这样的啊， 后面的一面呢，我们用书线勾勒一下啊，菱长为二十厘米，那么菱长就是这里啊，二十，这里二十，好，好从上面截出一段，表面积减少了四百平方厘米，从上面截出一段就是上面啊，就这 前面画实线啊，看着吧，那么后面看不到的呢，我们就画竖线啊， 好，第二就是从这个红线的这个地方把它切出一点上面的一段，那么这个它的表面积就减少了四百平方厘米。 你们想从上面切出一段以后啊，这上面的一段也是一个长方体的上面，这这这么多没有了。这个长方体的上面一面切出以后，下面也同样的增加了 一个里面啊，这个红线，这个也是正方体，跟上面这个正方体它是一样的，所以它的表面积减少的部分呢，应该就是只有那个，只有这四个面，是吧？哎，这前面这个面， 哎，还有后面这个面，右边这个面，还有左边这个面，哎，我们用竖线表示，好，这样四个面 他的每个面都是一个长方形，而且他的长二十宽，都是截出这一段啊，宽，我们不知道，这是我们要求的啊，先把这个宽求出来，也就截出这一段有高多少啊，这个理我们就要好好的啊，来想一想，既然减少了四百平方厘米，那么也就是说四个面一共是四百平方厘米，那么一个面应该是多大呢？ 四百是四个面的，那么以每个面就是说啊，把它求出来，是吧？可以除以四，哎，这样就等于多少呢？这是一百 平方厘米吗？是吧？一个面是一百，而它的宽是多少啊？对，因为它是个正方形啊，所有的零长都是二十啊，那么这个地方也是二十，长方形的面积等于长乘以宽，那么宽不就是把面积 除以长吗？对不对？除以二十，对，对，就是五厘米吗？哎，好，这个地方就是五厘米了，是吧？这是五厘米啊，这就是五厘米，对吧？那你们想一想，下面这一段是多少呢？我们要求剩下的一段的体积，对不对？剩下一段的体积 它是一个长方形，剩下的一段是一个长方形，它的长是二十，宽是二十，高是多少？我们不知道这一段，哎，把它取出来就可以了啊，这一段是多少？上面是五厘米，下面一段就是把二十，这总的二十减去五厘米，是吧？ 二十减去五厘米等于多少？这个我们要算一算，就等于十五厘米，是不是？哎，这么多，十五厘米，对吧？好，那么下面一段长方形的体积就算出来了，是吧？长乘方乘高，对吧？这二十乘以二十，再乘以高， 哎，四百再乘以十五，是吧？哎，等于多少？四乘以十五，对吧？六十再加两个零，哎，单位是什么？哎，是体积单位啊，是一方厘米。

你永远也干不过一个从四年级开始就学几何模型的孩子，因为他们清楚的知道，小学四到六年级的数学，考来考去，就这九大几何模型把它们吃透。考试就好比翻书抄答案。这个是一半模型， 无论一点怎样变，阴影面积始终是长方形面积的一半，这是等高模型，又叫拉窗帘模型，同底等高，无论位置怎么改变，三角形面积都不会变。这些几何模型，这本玩转几何都总结好了，并汇总了九大几何模型。像三角形就有等高模型，秒头模型、 沙漏模型，四边形就一半模型、蝴蝶模型，圆形就曲线模型。考试碰到哪种模型往上套，就能快速得出答案。而且孩子还可以亲手演示模型的推导过程，将复杂的几何知识变得可直观，孩子也更容易理解。学完后还有相关题型， 及时检测学习成果。利用好这套书，后面初中学几何会更轻松。快给孩子安排起来吧！你永远也干不过一个从四年级开。

哈喽，宝贝们，大家好，今天我们学习两种线之间的关系，一个叫平行，一个叫垂直。那我们可以看到图上的一二三四， 这些图中其实可以把线的情况主要分为两大类啊，主要就用相交和不相交来进行判断。可以看到图一，他们很明确的有一个相交的焦点，那第一个图肯定是相交的情况。 第二幅图呢，虽然看似没有相交，但我们知道通过直线可以两段无限延伸的特征，那他们在更加靠右的一些地方，虽然没有画出来，但我们知道他终究是会相交的。那第三条呢，可以看到两个线段无论往两段怎么样延伸，他们是不是中间的距离都是处处相等的，所以他们会延会相交吗？ 其实不会的啊，所以第三个图形它是唯一一个不会相交的情况。而最后一个图形呢，同样它也是已经有了这样的相交的一个焦点了，所以它一定是会相交的。 好，那我们总结一下，我们把这样的图形分为相交和不相交的两类，那这种相不相交的呢？我们会把这样的同一平面内，这样的永远不相交的两条线呢，叫做什么呀？ 叫做平行线，那么也就是说这两条直线他们互相对对方来说是互相平行的。 好，那这个是不相交的情况，那相交的情况当中呢，我们也分为两类啊，我们相交会形成一个角度，那当中有个特殊的角度，我们会有一个特殊的名称，也就是两条直线形成九十度的一个直角的时候，我们就会说这两条直线 互相垂直，所以找两条直线是否互相垂直，我们就找哪个特点，就看它是否形成直角，是否有九十度的角就可以了。 如果两个互相垂直的话，他们就一条直线叫做另一条直线的垂线，这样一个交点有名字哦，既然是垂线，那垂线相交的点呢？我们就叫它垂足，没有想到吧，不叫垂点，不叫交点哦，叫做垂足，要记清楚啦。 好，那反过来，我们想要表示出这一个线之间的关系是互相垂直的状态，我们就缺不了什么呀，一定是要把这个交点他的一个角度九十度的特征表现出来。所以如果要画垂直的话，我们一定不要忘记。什么符号呢？ 直角符号一定是不能忘记的哦，就像图四老师圈起来这个符号一样，像是一个七的一个形状，这个直角符号一定不要忘记了。 接着我们来看一下三条直线之间会存在什么样的关系呢？那看第一个左边的，我们知道有两两直线互相平行，我们的 a 和 b 呢互相平行， b 和 c 呢也互相平行，那么我们的 a、 c 之间会有一个什么样的关系呢？ 我们知道平行线间的距离是处处相等的，因为它们之间距离处相等，所以不管它们不管怎么样，两段无限延伸，是不是因为距离是一样的，所以不会越缩越紧，形成一个交点， 那么就说明 ab 之间有一个这样的相等的距离， bc 之间呢，也有一个相等的距离，那么 a 和 c 之间，那这个相等的距离是不是也会是一个固定的值？既然 a、 c 之间的距离处处相等，那 a、 c 会不会相交呀？ 既然永不相交，那说明 a、 c 之间的关系就是互相平行。好，那接下来看一下垂直之间的关系哦，我们知道 e 和 g 是 互相垂直的， f 和 g 呢，也是互相垂直的， 那么我们 e 和 f 之间会是什么情况呢？这个信息在初中大家就会学到，有一个定律叫做同位角相等，两直线平行。 那给大家做一个小小的拓展来看啊，也就是他们之间的这一个角度都是九十度，角度相同，所以他们一定是 互相平行的。但是大家还没有学习到这么高难度的内容，那大家其实从图上来看也是可以看到啊， e、 f 之间的距离处处相等，所以平行。那还可以怎么来看呢？其实我们在 e、 f 之间 加一条线段，那这一条线段垂直于 e 和 f， 我 们就可以看到老师在图上是不是做出了一个完整的什么形状？长方形，因为有都是九十度的直角，所以这个长方形它的特征是两组对边且平行的线段。 那既然是两组对边且平行，那我们是不是说明 e、 f 互相平行呢？所以不管是根据初中的知识，还是根据我们图上去看到的，以及做出来的这个长方形，我们都可以得到 e、 f 之间的关系。同学们，这两种特殊的形状搞清楚了吗？ 好，来看一下今天的例题。在我们的平行和垂直中，他的考法往往很灵活很多遍，同学们对于他的题目一定要自己想清楚了，看有没有什么样的不一样的条件，还有没有提到的情况，或者说我们能想出一个反例呢？ 好，第一个，不相交的两条直线叫做平行线，这是一个常见的考法，并且这个说法是大错特错的，为什么他缺少了一个重要条件？哪个条件？ 同学们可以把两个手伸出来，比如说笔像一个大大的叉，并且这两个叉之间是有一定的空隙的，我们会发现这两个叉 好像是不相交的，对不对？但是他是平行线吗？绝对绝对不是哦，为什么有个重要的天角线，他们不在同一平面内， 所以同学们只要是说平行线，他们都有一个重要的前提条件哦，一定是在同一平面内，才能这样来讨论他们之间的一个关系，不在同一平面内，那绝对是不可以的。 好，第二个，同一平面内两条直线不不平行就一定垂直，这个好像 有点道理，因为我们不是学的就是平行和垂直的关系吗？那不是平行就是垂直。好像说的没什么问题啊。但是同学们，我们在今天的第一个知识点就讲到了，他们是不是之间还可能形成除了九十度以外的任何一个角度呀？ 三十度、六十度，七十五度、三十八度是不是都可以啊？所以这句话也是大错特错的哦，他们还有很多种可能互相交集的情况。 好。 c， 两条直线互相垂直，这两条直线相交所成的四个角一定都是直角，这句话对不对呢？ 那老师在前面讲到了，互相垂直形成的角一定是直角，那一个平角当中那有一个直角，另一个角也会是直角，那对面的一个平角当中是不是也是同样情况，所以四个角一定是直角，这句话是正确的。最后一个，同一平面内，任意一条直线都只有一条平行。 那老师刚刚是不是在支点二讲到了一条直线真的只有一个平行吗？我们会发现 ab 和 ac 以及 bc 是 不是两两平行呢？ 画出来的三条直线当中，每一条直线都有两条平行线，还有那么多没有画出来呢？一条直线，它其实有几条平行线呢？是有无数条平行线的，你是画不完的。所以这句话也是大错特错，都有无数条平行，这个定力要牢记哦。 好同学们，今天平行和垂直的概念以及应用题就到这里了。这个内容上孩子们很容易出错，平常在实战练习中一定要总结经验，总结教训，对错题一定要把它搞清楚，搞明白，下次不要再犯同样的错误，就非常非常棒了。好同学们，我们下课。

大家好，今天我们画一副太空主题简笔画，喜欢的话先收藏加关注哦！火箭位对称结构，用铅笔起稿，两边画出对称的几何图形， 宇航机器人也未对称结构，画出中线，两边画出对称结构。 看到这里了，喜欢的同学动动小手点个赞吧！ 铅笔齐稿画好后用黑色勾线笔描边， 注意不要描出辅助线， 描出轮廓后查掉多余的铅笔线稿。 太空宇宙主题画画好了，我们去涂颜色吧！ 看更多好看作品请收藏加关注哦，下期再见啦！

名著速通馆，十分钟读懂平面国二维世界，藏透阶层与真理的终极困境！ 欢迎走进名著速通馆，每期十分钟，用通俗故事带大家吃透一部经典名著，不用啃厚重圆柱，也能摸清核心脉络，读懂深层内涵。 今天要聊的这部书，堪称百年前的科幻哲理神作，没有复杂剧情，只用几何图形构建二维世界，却把等级固化、认知局限、真理传播的难题，写得戳心又透彻。他就是埃德温 a 艾伯特的平面国。 咱们跟着主角的经历，十分钟解锁这个藏满隐秘的奇特世界。先搞懂核心设定。平面国里没有高度和厚度，只有长度与宽度， 所有居民都是几何图形，而形状直接绑定身份等级森严到没有半点变通，空间完全是刻在骨子里的阶层划分。最底层是等腰三角形，大多是工人士兵， 顶角越尖越卑微，还因尖角易伤人，被视作危险群体。网上是等边三角形算平民，上层拼尽全力才有机会升级成四边形， 再网上是正方形、五边形、六边形这类多边形，边数越多地位越高，对应商人、官员、学者等体面之业。 顶层则是圆形。贵族不是天生完美圆形，而是靠代代生育增加边数。 边数多到肉眼看不清棱角，就成了伪圆形。边数越接近圆形，权力越集中，掌控着平面国所有规则。更窒息的是性别与生育规则。女性全是线段，没有任何边数， 地位比底层等幺三角形还低。走路必须不停发声提醒男性避让，一旦不小心碰撞，轻则受罚，重则处死。 生育完全服务于阶层固化，贵族孩子边数会比父母多一条，稳不升级底层等幺三角形大多只能生同类， 想突破阶层难如登天。咱们的主角就是平面国里一个普通的正方形。艾伯特和作者同名，做着商人的营生，守着既定规则安稳度日。 直到两次特殊经历彻底击碎了他的固有认知。第一次是一场颠覆认知的梦，主角闯进了宪国，一个只有长度没有宽度的异维世界。 宪国军民全是长短不一的线段，只能沿着直线前后移动，看不到左右方向，更无法理解宽度的存在。 宪国国王是最长的线段，统治着所有短线段居民，在他们眼里，前后就是世界的全部，自己的世界就是最完美的存在。主角忍不住跟国王解释说，有宽度， 有平面国这样的二维世界，可国王根本不信，还觉得他是传播一端的疯子。在国王的认知里，超出长度的一切都是幻想，甚至威胁要消灭主角。 梦醒后，主角满是困惑，自己能看清现国的局限，那会不会还有更高维度的世界是自己看不到也理解不了的？这个困惑很快有了答案。第二次经历比梦境更离奇。 平面国千年庆典之夜，主角独自在家沉思，突然眼前出现诡异景象，一个点慢慢变大成小圆，接着不断膨胀，到最大，又逐渐缩小回点，最后消失不见。 主角又怕又好奇，试探着询问对方身份，得到的回答震惊全场。我来自三维世界是球体，你看到的变化只是我穿过你们平面国时你能感知到的部分，主角完全听不懂三维世界球体，就像当初现国国王听不懂平面， 为了让他理解，囚体直接把他提出平面国，带进了三维世界。那一刻，主角的认知彻底崩塌。他第一次看清了平面国的全貌， 住了一辈子的房子，熟悉的同胞都多了厚度这个新维度。平时高高在上的原型贵族，在三维视脚下也只是带厚度的多边形，再也没有了往日的威严。 球体还告诉他，认知会被所处维度局限，现国看不到宽度，平面国看不到高度。 三维世界之外，还有更复杂的维度世界，远比想象中多元。主角彻底开窍，恳求球体带他看更高维度的世界，却被拒绝。球体让他先把三维真理带回平面国，让更多同胞突破认知局限。 可主角没想到，传播真理的路远比想象中艰难。他先找亲友分享三维经历，说有球体、有高度，有三维世界， 可所有人都觉得他疯了。在大家眼里，平面国就是世界的全部，高度三维全是无稽之谈。他又找原型贵族求助，想靠贵族的影响力扩散真理， 可贵族们不仅不信，还瞬间警惕。平面国的权力根基全靠形状定等级的规则，一旦承认更高维度，现有规则会被颠覆，他们的权力也会动摇。 为了维护统治，贵族们给主角扣上传播异端、扰乱秩序的帽子，直接把他关进监狱，还下令禁止任何人谈论三维相关话题。 主角在监狱里待了十几年，从最初的愤怒、不甘，慢慢沉淀出清醒的认知。 低维度的局限就像无形的枷锁，困住了大多数人，真理的传播往往要对抗既定规则固化阶层，还要打破人们不愿突破的认知惯性。就像宪国国王看不到平面，平面国居民看不到三维， 现实里的人也常被所处环境固有认知束缚，很难接受超出认知的真理，甚至会排斥、打压提出真理的人。即便如此，主角始终没放弃在监狱里写下自己的经历， 希望未来有一天，平面国居民能突破维度局限，接纳三维真理，也想提醒所有人，认知没有尽头，别被眼前的世界困住， 更别轻易否定超出认知的事物。其实平面国看似是维度科幻，故事本质全是对现实的辛辣隐喻，几何形状对应的等级划分，就是现实里的阶层固化， 顶层垄断权力，底层难以上升。主角向现国国王、平面国居民解释更高维度的困境，对应着现实中真理传播的艰难， 新思想、新认知，往往要经历质疑、打压才能慢慢被接纳。而维度认知的突破，更是在提醒我们，要保持谦卑与好奇，别被固有认知框死。世界远比我们看到的更复杂， 百年过去，平面国依然被奉为经典，不是因为科幻设定超前，而是他藏着的哲理永远适配现实。阶层固化的无奈、认知局限的束缚、真理传播的坎坷， 直到现在仍值得我们深思，这也是这部小说能跨越百年的核心原因。以上就是今天名著速通馆带来的平面国，十分钟走完主角的维度认知之旅，吃透故事脉络与深层隐喻，不用啃原著也能 get 到经典核心。 名著速通馆始终用通俗语言讲透经典，用简洁节奏梳理故事，让你花最少时间读懂最多名著。下期咱们切换风格， 走进科幻大师飞利浦 k 迪克的经典少数派报告，看未来世界，预测犯罪系统如何颠覆正义与自由。剧情反转不断，内涵直击人性。感兴趣的朋友别忘了点赞关注名著速通馆，下期不见不散！