八上几何题解压书写
粉丝2.8万获赞8.1万
相关视频
 05:36查看AI文稿AI文稿
05:36查看AI文稿AI文稿八、上数学压轴系列之几何中的折叠问题关于折叠问题,只需要记住一句最核心的话,折叠本质上就是轴对称变换。根据之前学过的轴对称变换的概念,即把原图沿着某条直线对折, 得到一个和它完全重合的新图形的变换过程,就叫做轴对称变换。那我们就可以知道,折叠前后的两个图形应该是完全一样,也就是全等。比如把三角形 a、 b、 c 沿着 a、 c 折叠成三角形 a、 b 撇 c, 那 这两个三角形应该是全等的。 有了全等这个基础,就能直接推出三个解析时可以秒用的结论。结论一,折叠前后两个图形的对应边相等。 比如左图中三角形 abc 折叠成三角形, ab 撇 c 后,原来的 ab 和折叠后的 ab 撇就是对应边,所以 ab 等于 ab 撇,原来的 bc 和折叠后的 b 撇 c 也是对应边,所以 bc 等于 b 撇 c, ac 是 这两个三角形公共边,自然也是相等的。 结论二,折叠前后两个图形的对应角相等。同样的例子,原来的角 b 和折叠后的角 b 撇是对应角,所以角 b a、 c 和折叠后的角 b 撇 a、 c 也是对应角,所以角 b a、 c 等于角 b a、 c。 结论三,折痕是折叠前后两个图形对应点连线的垂直平分线,对应点就是折叠后重合的点。比如这里的 和 b 撇,他们的连线是 b、 b 撇,而折痕 a、 c 就是 b、 b 撇的垂直平分线,意味着折痕 a、 c 垂直于 b b 撇,折痕 a、 c 平分 b b 撇,也就是说 b 到 a、 c 的 距离和 b 撇到 a、 c 的 距离相等。 ok, 以上就是折叠问题中最关键的几个结论,我们来做一道题,看看如何应用在三角形 a、 b、 c 的 距离和 b 撇到 a、 c 的 距离相等。 ok, 以上就是折叠问题中最关键的中点, ok, 以上就是折叠问题中点 d 边的中点 连接 b、 d 把三角形 b、 d、 c 沿 b、 d 翻折,得到三角形 b、 d、 c 撇,把这个三角形沿这条边翻折,得到这个三角形。所以根据折叠的性质,我们知道这俩三角形应该是什么全等。还有一组条件,若 a、 d 等于 a、 c 撇等于二, 这条边和这条边相等,都等于二, b、 d 等于三。求 b、 c 边的长,让我们求这条绿色线的长度,同学们可以暂停视频先思考一会, 一起来看一下。根据题干当中的条件,点 d 是 a、 c 边的终点,所以 d、 c 和 a、 d 边相等, 它也等于二。我们又知道三角形 bdc 和三角形 bdc 撇是通过翻折得到的,所以根据翻折的性质,对应角相等,对应边相等,所以这俩角相等, dc 和 dc 撇也相等,所以 dc 撇 也等于二。哎,那这样子我们就又有了一个重大的发现,同学们看这条边,这条边,这条边,它们都是等于二的吧。 所以这个三角形 a、 d、 c 撇原来是一个等边三角形,既然它是一个等边三角形,那么这个角它就等于六十度。那刚才根据折叠的性质,我们又知道这俩角相等,所以它们分别也都是六十度。 现在让我们求的是 bc, 那 根据翻折的性质, bc 和 bc 撇是相等的,所以假如我们能求出这条线段的长度,那也是可行的吧。 那接下来这条线段,或者说这条线段到底应该怎么求呢?如果同学们仔细听了我们刚才对于这个折叠问题的描述,那么我相信大家一定能够想到一条辅助线,就是什么 连接 c c 撇,连完以后,我们就能得到这个 c c 撇和 b d 是 垂直的焦点呢,我们把它记作 m 点。 原因前面我们也解释过了,折叠的本质是轴对称变换,所以折叠后除了得到对应边相等,对应角相等,那么折痕是对应点连线的垂直平分线。 这个结论很多时候都是解析的关键。比如说对于这道题,假如同学们能够想到连接 cc 撇,那么这道题基本上就已经结束了。 看,连完以后,这里出现了一个直角,那么有了这个直角,我们再能求出 c 撇 m 和 b m 的 长度,那么根据勾股定律,很快就能算出这个 bc 撇的长度吧。 这里等于六十度,这里是直角,那这个角它就是三十度,那根据三十度所对的直角边是斜边的一半,所以 dm 它就等于一, 那 dm 等于一。利用勾股定律,我们又能算出来这个 c 撇 m, 它就等于根号三。再看 b d 的 长度,我们又知道它是等于三的,那 dm 等于一,所以 b m 等于二。这样的话,在直角三角形 c 撇 b m 当中,两条直角边的长度都有了, c 撇 b 的 长度也就出来了啊。 c 撇 b, 它是等于根号下 c 撇 m 的 平方,再加上 b m 的 平方,算出来等于根号 七,所以这道题我们要求的这个 bc 的 长度,它就等于根号七。好,那通过这道题呢?希望同学们对于这个折叠问题的常见结论一定要牢牢掌握, 尤其是这个第三条折痕式对应点连线的垂直平分线,很多时候都是我们解题的突破口。 ok, 那 这节课就讲到这里,拜拜。
277Tom张数学 03:45查看AI文稿AI文稿
03:45查看AI文稿AI文稿今天这道八上几何题真的超级难,好,我们来看题。首先他给了我们一个等腰三角形 a、 b、 c、 d 点在 a、 c 边上,并且角 a、 b、 d 和角 b、 a、 c 之间有这么一个关系, 然后一点在 b、 d 上,并且 b 一 等于 ab, 接着再过一点做 ab 边的垂线。题目问,若 b 积等于二十四,三角形 ac 的 面积等于八十五点五,让我们求 bc 的 长度。 好,我看原视频这个同学他用了四组全等,虽然说是略微麻烦了一丢丢啊,但是我经常跟你们说,不管黑猫白猫,抓到老鼠就是好猫,所以说这位同学的做法还是值得肯定的。 那接下来我就跟大家分享一下我的解法。首先这个角度关系明显是在提醒我们需要倒角, 那可以看到角 d、 e、 f, 它是三角形 b、 e、 f 的 外角,所以角 d、 e、 f 减去角 e、 b、 f, 也就是角 abd 了,它也等于九十度, 那也就是说角 d、 e、 f, 它和角 b、 a、 c 是 相等的,那它们俩的补角自然也是相等的了。如果再想到 b、 e 等于 ab 这个条件的话,我们是可以考虑延长 c a, 然后再过 b 点做垂线的, 这样我们就得到了角 b a、 h 等于角 bo f, 然后就能证明三角形 bo h 和三角形 bo f 全等了,全等之后就得到了 bo h 等于 bo f。 好,那接下来再怎么走呢?我们的数据都在 bc 这条边上,而我们的辅助线在上面,那我们如何让上下两个部分产生联系呢?这里就需要认真思考一下了, 不知道你们注意到了没有啊? b f, 它在直角三角形 b、 f、 g 中,而这个三角形斜边 b、 g 的 长度是已知的,还有一个角 f g 也算是比较显眼吧,因为它也是等腰三角形 abc 的 底角嘛。 这里我是这样想的,如果我们继续延长 a h, 并且令 h k 等于 f g 的 话,然后再连接 b、 k, 那这个三角形 b、 h、 k 就 和三角形 b、 f、 g 全等了,所以我们就得到了 b k 的 长度是二十四, 然后还有角 h b、 k 等于角 f、 b、 g。 可以 看到这个角 k, 它和贝塔是互余的关系,所以这个角 k、 b、 c 它应该是九十度的。 而又由于 ab 是 等于 a、 c 的, 你们看斜边中线是不是出来了呀?也就是说 a 点现在是 c k 的 中点。 如果我们连接 k、 g 的 话,那三角形 c、 k、 g 的 面积就等于三角形 a、 c、 g 的 两倍了。 而由于这个三角形 k、 b、 g 是 一个等腰直角三角形,所以它的面积也能算,然后我们把它俩一加,不就是这个大三角形 k、 b、 c 的 面积了吗? 其中一条直角边 b、 k 的 长度我们已经知道了,现在要求另一条直角边 b、 c 的 长度,那这个是不是用面积法就行了?最后算出来 b、 c 是 等于三十八点二五的,你学会了吗?
1224五星几何兔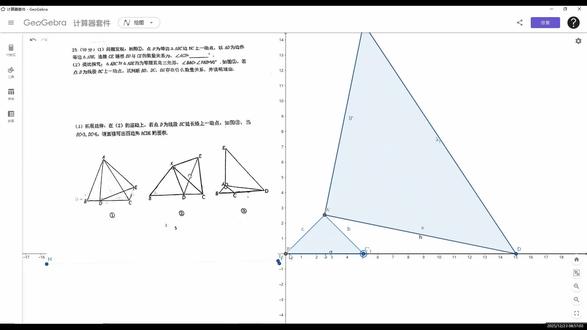 06:08查看AI文稿AI文稿
06:08查看AI文稿AI文稿看这道题,咱们看这道题,前两问比较简单,不说了,直接看第三问。这道题是一个八年级的一个探求题,三角形勾股定律,这块三角形考了个手拉手, 直接看第三问,拓展延伸在括号二的基础上,那还得看看括号二,括号二它俩是等腰直角三角形,这个是九十度一个洞点。这个简单,我们在括号二就能知道。有两个三角形全等 拉手吗?有两个三角形是全等,那咱们迁移一下,就得在括号三这找到那两个全等的三角形。简单了,把图放一下,当 bc 等于三, cd 等于六的时候, bc 等于三,那这个不行,画多了是不是得画到三 三,这对在三这个位置,这个直接求四边形 a、 c、 d、 e 的 面积。直接求四边形 a、 c、 d、 e 的 面积,那这个四边形 a、 c、 d、 e 的 面积,它等于啥呀?它等于三角形 a、 c、 d 的 面积,然后加上三角形 a、 d、 e 的 面积, 咱们就把这俩三角形的面积求出来就行。这里 c、 d 等于六,然后的话这个 bc 等于三。那我们直接就可以做高了呗,支到底。然后的话,把这个过点 a 做垂直三角形 a、 c、 d 的 高就算出来了,是不是?所以咱们先把这个高给做出来,做个垂线呗, 过点 a 的 一条垂线,描个点好, a、 g 就是 它的高, a、 g 就是 它的高。 看着有点长,看着有点长,咱们连一下,这回应该行了,这回应该行了。好, 然后的话由括号二嘛,根据括号二的条件,那肯定是还得是手拉手找全等,所以说咱根据括号二,咱把这个 c、 e 也给它连上 ce 连上的之后,那咱们根据括号二就有这个全等条件嘛。哪两个三角形全等?三角形 a、 c、 e 和三角形 e, a, b, d 全等, a、 b、 d 全等,能得到的就是啥?就是 c e 等于 b, d, 三加六得九, ok 吧?太简单了,然后的话咱就往里弄数呗。先求这个 a g, 先求这个 a g, 这个 a g 等于啥呀? bc 是 三,那这个就是二分之三,对吧?这是垂直的,这个四十五度等腰直,所以这个也是二分之三。 c e 是 九, cd 是 六,我可以直接勾股定力,求求这个第一。勾股定力求第一, 那第一是不是应该等于根号下 c、 e 的 平方加上 c、 d 的 平方, 等于根号九方加六方?整理一下,九方加六方,八十一加三十六,是不是八十一加三十六,等于三倍的根号十三,这三倍的根号十三就是 d e 的 长, d e 的 长。知道 d, e 的 长了,我们还可以求 a e 或者是 a d 的 长,因为它不是个等腰值吗?对不对?它不是个等腰值吗?这个是四十五度,这个是四十五度。这块这个是直角,用不用推一下? 这块是直角,用不用推一下?说一下吧,说一下这块这个角,这俩全等了吗?这个点和这个点相等, 对吧?那这块这个角他就等于四十五度,减这个点,这块这个大角等于四十五度,加上这个点,所以这俩角相加还是得九十度,所以这个角是九十度,这才能用勾股定律,这才能用勾股定律。 然后的话,现在我已经知道 d e 是 多少了,我想求这个 a e 是 多少? a e 和 d e 是 根号二倍的关系,根号二倍的关系是啥呢?是这个 a、 e 等于二分之根号二倍,或者是它除以根号二。 谁除以根号二?是这个或者这么写吧,根号二倍的 d、 e 等 a, e 等于 d, e, 那 d, e 知道了,那 a、 e 它就等于啥呀?这个 a、 e 等于根号二分之一倍的,这个 d、 e 也那个分母有理化,二分之根号二倍的 d, e, d, e 是 三倍,根号十三,三倍根号十三,然后就乘呗,对不对?那它就等于啥?等于二分之三倍的根号二十六。 这就是 a、 e, a, e 还得 a, e 乘 a、 e, 然后再除二,是不是就是三角形 a、 d、 e 的 面积? 然后就来吧,三角形 a、 c、 d 的 面积加上三角形 a、 d、 e 的 面积,三角形 a、 c、 d 的 面积等于二分之一乘以 c, d 二分之一乘以 c、 d, 然后再乘 ag。 三角形 a、 d、 b 的 面积,那它等于二分之一。 a、 e 乘 a、 e。 也可以用 a、 e 乘以 a、 d 往里弄数,是不是二分之一乘六?乘二分之三,加 二分之一乘二分之三倍,根号二十六的平方也行,那咱就再乘一个二分之三倍的根号二十六。数我就不算了,数我就不算了。它等于啥?等于四分之一百三十五。
29孙悟能 05:21查看AI文稿AI文稿
05:21查看AI文稿AI文稿等腰三角形、全等三角形、直角坐标系以及含有特殊角的直角三角形,这些都是八年级上册数学中的重要内容,它们不仅自身有着关键的知识点, 更常常综合在一起,以压轴题的形式出现在试卷的最后部分。接下来我们就一起看看他们是如何相互结合,形成综合问题的。由这个已知条件,我们知道什么?我们知道 ab 等于 ac 的, 而且这个角是一个直角,这说明 abc 是 一个等腰直角三角形。 现在是要求点 b 的 坐标,那点 c 的 坐标我们知道是二二负二。充分利用已知条件, 那我们做过 c 点做 c h 垂直于 x 轴,那很显然我们就知道这两个三角形是全等三角形, 为什么?因为 a、 c 等于 ab, 而且这个角和这个角是互补的,不余,都相加起来得九十度。 而在这个直角三角形里面,这个角加上这个角也是九十度,所以很自然就可以推出这个角等于这个角。又因为这个是这两个都是直角三角形,所以根据 a、 a、 s 就 可以判定 这两个三角形都是怎么样的。是全等三角形,所以很快就知道这个 a 点的坐标是多少。 因为 o a 就 可以推出 o, a 是 等于 c h 的, c、 h 长度是二,那 o a 的 长度也是二 o a, 所以 o a 长度是二,所以 o a 点的坐标是负二零,那知道 a 点的坐标,那 a、 h 的 长度是多少? a h 的 长度是四吗?知道 a、 h 的 长度,那就知道 ob 的 长度, ob 的 长度也是四,所以 b 点的坐标是什么? 零四,好,很快就可以解。解答出第一个 好,那看第二点, c、 a、 c、 b 分 别交坐标轴于 d、 e。 求证 三角形 a、 b、 d 和 c、 b、 d 的 面积分别相等。看一下,要求这两个部分面积相等,那我们现在知道什么?它们有个公共的底边 b、 d, 那 我们只要证明它们的高相等,那自然它们的面积就相等了。是不是 它们像这个三角形 b、 d、 a 的 这个面积,这个高度,这个高度是多少?是二嘛?就是 o, a 嘛,它的高就是 o, a 就 二。然后呢,这边这个三角形它的高是哪一个?就 c 点到 y 轴的这个距离嘛,也是二, 所以现在它们的高一样,所以它的面积就自然而然就相等了。好,这第二问也解决了。 连接 d, e, 求证 b, d 减 a, e 等于 d e, 那 就是说在 b、 d 上剪起截掉一段长度是 a、 e 的 一段,假设在这一点 m, 使得最后要证明什么?要证明这个 d、 m 和 d、 e 相等就可以了,是不是?那我们最好是要把 am 连接起来,是不是?连接起来以后,因为我们之前挣过 这个角角一和这个角角二是相等的,是不是?那很容易就可以证什么这两个三角形全等,因为 ab 又等于 ac, 现在 接起的这一段 b、 m 是 等于 a、 e 的, 所以这两个三角形全等一全等,我们就可以证出什么 a, m 等于 e、 c, 又因为 这一个角 o、 a、 d 是 等于角 c 都是四十五度,因为刚才我们这里 正出来全等这个角和这个角四十五度嘛,因为这里是一个直角,所以这个角等于这个角也是四十五度。又因为根据他们的坐标,我们都就知道这个 d 点正好在 a d 的 中点嘛, d 点是 a d a c 的 中点,所以 a d 又等于 c d, 所以呢就可以证明这个 a d o 和 b d e 是全等的,一全等我们就可以证明出 dm 等于 d 一, 所以最后就可以证明出 b d 是 减去 a 一 等于 d 一 的。整个解析思路就是这样子自己去写,这样子能够加深自己的印象。
 03:36查看AI文稿AI文稿
03:36查看AI文稿AI文稿终点中线是初中几何中非常重要的知识点,学完全等三角形考察他们的题型也是非常多的。今天再带大家学习一个几何模型,倍长中线模型。什么是倍长中线呢? 给了一个三角形 d 是 bc 边上的中点,连接顶点就是中线。我们延长这条中线 a、 d, 使它的长度呢增加一倍到一点,我们再连接 b、 e 或者是 c、 e, 这就是基本的倍长中线的辅助线做法。这样呢,我们就形成了一个八字全等结构,因为 d 是 中点,那 b、 d 就 等于 c, d, a, d 呢,又等于 d, e 加上一组夹角,对顶角相等 s a s, 那 这两个三角形就是全等的。全等之后呢,我们还能得出几个结论,对应边 a、 c 就 等于 b、 e。 另外呢,对应角的这个角和这个角是相等,它们又是一组内错角,那是不是 a、 c 就 平行于 b、 e, 所以说 a、 c 和 b、 e 是 平行且相等的。这里面我们也可以不连接 b、 e, 连接 c、 e。 结论也是一样的,解题时要根据题干条件决定连接哪边。这个呢,是最基本的被长中线的结构, 我们把它叫做基本型,很容易识别,考试时有可能不直接这样考,那就有了第二种变形,如图呢,给了一个图形,依然告诉我们 d 是 bc 的 终点, 但这次他没有给出中线 a、 d, 而是在 a、 b 边上任意一点 e 给了我们这样一条线段 d, e, 我 们给他取个名字叫内中线吧。此时我们依然可以沿用倍长中线的思路,延长 e、 d, 使得 e、 d 等于 df。 同时呢,我们连接 f、 c, 同样能够构造八字全等结构,那这两个三角形呢,也是全等的, b、 e 和 f、 c 也是平行且相等的,这种呢,我们把它叫做倍长中线的中点型,或者是类中线型。 还有一种呢,就是给了两条平行线中间加一条线段,知道他的中点连接到一条平行线,那么我们可以延长这条线段与另外一条平行线相交,也是可以得出这两个三角形全等的结论。这个我们就把它叫做中点加平行线形。不过这里的辅助线 不是倍长,而是延长相交。做题时我们要严谨一些,我们来做道题,如图 d 呢,是 bc 的 中点线段, b e 交 a c 域点 e 交 ad 也点 f, 又告诉我们 a e 等于 ef, 让求 a、 c 等于 b f, 证明两条线段相等呢。首先我们要考虑三角形全等,但是这两条线段好像也没办法在两个全等的三角形中。 题目中又给了两条线段相等和一个中点,大家看一下,我假如遮住上面这一部分,这个图形熟不熟悉, 是不是就是我们刚才讲的内中线的倍长类型?刚好这个 b、 f 就是 两个全等三角形的一条边。我们尝试一下延长 f d 到 g, 使得 f d 等于 d g 连接 c g, 马上我们就能得出三角形 b、 d、 f 是 全等于三角形 c d g 的, 那么 b、 f 就 等于 c g, c g 和 a c 刚好就在一个三角形中,证明它们俩相等就行了。因为全等对应角,角一和角二是相等的。 同时 a、 e 等于 e f, 那 么角三呢,就等于角四,角一和角三呢,又是对顶角,那么这四个角都是相等的,等角对等边,那么 a c 就 等于 c g 也就等于 b f 了,得正下课。
 06:12查看AI文稿AI文稿
06:12查看AI文稿AI文稿继续说题,这道题也是前边几问比较简单,咱们就不说了,直接说第四问弱点, m 在 线段 cd 上, m 在 线段 cd 上 连接 mpme, 直接写出 mp 加 m, e 的 最小值,那这里边我把这个图画完了,我把 m 标一下,也不用太费话,将军印马是不是?好,这个就是 m 点, 这个图是咋做的?这个原图在这我给它画完了,我是做了这个 e, 因为 e 它是一个定点,对不对?我是做了一个 e 关于 c d 的 一个对称点,一撇又过,这个一撇 做 bc 的 垂线点到直线,点到直线距离,是不是点到直线距离垂线段最短,那么这个时候当和 p 三点共线的时候,三点共线的时候就是它最短的时候。 因为这个 m 是 在一撇和 e 它的这个垂直平分线上,所以 m 到一撇的距离等于 m 到 e 的 距离, m 到一撇的距离等于 m 到 e 的 距离,它也挺有意思,它这个时候想让咱们求 cp 是 多长, cp 是 多长, 那这个就容易了,对不对?咱先把这个些已知条件,咱先往上标一标,提提已知了,这个是九十度,这个是六十度,这个是三十度,是不是还告诉了 ac 等于六, a c 等于六,这是六十度,那这一圈都是六十度,不是,这一圈都是六,都谁是六呢?这个 a c, e, c, e 等于 a, c 等于 a, e, 撇 都等于六,这一圈,对吧?然后的话,那么咋求这个 c p 呢?咋求这个 c p 呢? 打到角就行,因为这里边这个 c 一 撇是已知的,是不是?咱们要在这的话,能知道点这个这个特殊角三十度,六十度,咱这就成了,是不是?那也简单呐,这块这个是垂直的, 是不是?这块这个是垂,这块这个是垂直的,对不对?然后的话给他这块做过来对称了,这能不能研究出是垂直的? 这能不能研究出来?如果要是研究不出来的话,咱就把这个 e 给它连接上看一下,连接一下这个。好嘞,那咱就倒一下呗,看看都得多少?是不是? 这个 e 和 e 撇是对称的,所以说这个 e 撇和是相等的,没有问题,对吧?然后咱再看这个 cpcmp 这个角,因为它这块的话不是 角平分线吗? c d 是 角平分线,稍等一下, c d 是 角平分线,所以这个角就是四十五度, 那这个角也是四十五度,这个角也是四十五度,这个角还是四十五度,没有问题了吧, 对不对?所以这块这个就是九十度,太简单了,对不对?也就是说是啥呢?一撇一,一撇 p, 它垂直于这个 bc, 不是?一撇 p 垂直于 bc, 然后的话一撇 p 还垂直于 cm, 那 这个时候的话,它俩就是平行的,是不是它俩就是平行的,谁平行呢?这个 m e 和 bc 是 平行的,这些咱都能推得出来,对吧?都能推得出来,那现在的话,角 b 是 三十度,角 b 是 三十度, 那它对应的是谁呀?谁是三十度?是不是角? c e 撇 p, c e 撇 p, 这个角对应的就是三十度,为啥对应的它是三十度呢?它是 c e m c e m 这个角就是三十度,因为 c e 和 b e 还相等,这也是三十度, 它俩还平行, m e 和 bc 还平行,那么它就是三十度, 它是三十度,它也是三十度。 ok 了,它是三十度, c e 是 六,三十度角所对的边等于斜边一半,所以 cp 等于三, cp 等于三。 ok, 咱们整理一下步骤,不写了,咱就说一下得了。是不是 这里边的话我先知道怎么的最短先做一点的一个对称点,然后的话过这个一撇做 b c 的 垂线,我还能导出来一撇也是垂直的,所以这里边有一个关键的步骤,是不是咱们能得出是平行 bc 的? 平行 bc, 然后的话 c e 它还是啥呀? c e 它还是这个中线。直角三角形,斜边中线等于斜边一半。 也就这个题用了直角三角形,俩性质全给用了。直角三角形,斜边中线等于斜边一半,和直角三 角形中三十度所对的边等于斜边一半。 ok, 是不是剩下的话就是一个倒角了?他是三十度,他也是三十度,这两个是全等的,或者是说对称的,他是三十度,那么这个 c 一 撇, m 也是三十度, 这又是垂直的三十度,角所对的边等于斜边一半, c 一 撇等于六,完事。
15孙悟能 14:17查看AI文稿AI文稿
14:17查看AI文稿AI文稿好,我们来看一下,这是中山市一中八年级上册最近周考的一道压轴题, 这是非常常见的一类题目,就是解几何 几何图形的一一类长线的常见的一类题目。 好,我们读一下题。 在三角形 a、 b、 c 中, ad 是 平分角 b、 a、 c 的, 所以这个角是等于这个角, 角 a、 b、 c 是 等于两个角 c, 角 b 是 等于两个角 c, 然后求证 a、 c 是 等于 a、 b 加 b、 d。 方法一,如图在 a、 c 上截取一段 a、 e, 这一段 a 一, 使得 a 一 是等于 ab 的, 然后呢,连接 d 一, 就可以得到这两个三角形是全等的。 这两个三角形全等。为什么?因为这边等于这边,这边是公共边,然后因为角平分线,这个角等于这个角。根据 边角边,这两个三角形自然就全等了。这两个三角形一全等,就得出 b、 d 是 等于 e、 d 的, 然后呢,还有这个角等于这个角, 这个角等于这个角。然后因为提议又给出角 b 是 角 c 的 两倍关系,所以这个角自然也是角 c 的 两倍关系, 这个角又是三角形 e、 c、 d 的 外角,所以这个角加这个角等于这个角,所以就可以得出角 c 等于这个角 e、 d、 c, 那就可以得出 e、 d 是 等于 e、 c 的。 最后就可以推出 a、 c 是 等于 a, e 加上 e、 c, 也自然就是 a、 c 是 等于 ab 加上 b、 d 的 好看。方法二, 方法二采取的是补短 a、 b 作为较短的一条线,所以首先把延伸 a、 b 到一,使得 b、 e 的 长度是等于 b、 d 的, 然后 也可以证明出这两个三角形是全等的。为什么?因为这里有一条公共边,然后呢, 这个角等于这个角,还有哪个条件?还有 这个角等于这个角和这个角是两倍角的关系,是不是因为这里等于这里,所以这个角一是等于角 e、 d 等于角 e、 d、 b 的 这两个角是相等, 又因为角 b 又等于这个两倍的关系,所以这个角 e 和角 c 又是相等的,所以根据什么 aas 是 不是 aas 就 可以证明这两个三角形是全等的,是不是?好, 那我们看一下这道题,下面这个第二小问的这个解析思路。 在下面四边形 a、 b、 c、 d 中, e 是 b、 c 上的一点,然后 e, a 是 等于 a、 d 的, 然后角 d, c、 b 是 等于两倍的角 b 的, 然后角 d、 a、 e 加上角 b 是 等于九十度的 探求 dc, 还有 c、 e 还有 b、 e 之间的关系, 那我们通过这个图,这通过这个图我们可以大胆的去预测,怎么样呢?我们先说解析思路,预测出 b、 e, 它是有可能是怎么样的?等于 c、 e 加上 d、 c 的 是不是?好,那我们怎么样去证明这它们之间的关系呢? 通过我们刚才的这个上面的这些例子的解析思路,我们怎么样在 b 一 上弦起一段 等于 cd? 好, 假设我们在这里 取一点 f, 使得 ef 是 等于 c、 d 的, 这里等于这里。因为 a、 e 之前给我们的条件有 a, e 是 等于 d、 e 的, 那我们接下来的重任就是什么?证明这个等于这个 就可以证明这两个三角形全等,是不是这两个三角形全等,最后证明这两个三角形全等,就可以推出 a、 f 等于 e c, a, f 等于 e、 c, 然后 b、 f 等于 a、 f 不 就可以完美的证明出 b, e 等于 e、 c 加上 c、 d 了吗? 那怎么样去证明这两个三角形全等呢?这里就是解的关键了。好,我们来说一下这个过程, 因为呢, e、 a 是 等于 d、 e 的, 所以这两个角是相等,对不对?这两个角相等, 那这三个角怎么样呢?这三个角加起来就一百八十度嘛,那就可以证明得出两个角 e、 a、 d 加上角 a、 e、 d 是 等于一百八十度, 又因为什么?又因为角 d、 a、 e 加角 b 等于九十度,所以 两倍的角 d、 a、 e 加上两倍的角 b 等于一百八十度。好,根据等量带货就可以得到什么 角 a、 e、 d 就 等于两倍的角 b 又等于。刚才什么又等于角 c, 是 不是这是提议给的?得到这里以后, 又因为什么? 这个三角形 d、 e、 c 的 外角角 d、 e、 b 等于什么?角 a、 e、 d 加上角 a、 e、 f 角 d、 e、 b 同时也是等于什么?角 c 加上角 e、 d、 c。 因为所以我们就可以得到什么就可以得到角 a、 e、 f 等于角 e、 d、 c 是 不是因为刚才我们证明出 a、 e、 d 是 等于角 c 吗?这两个不就这两个相等不就消掉了吗?是不是就可以证明出来 a、 e、 f 等于角 e、 d、 c 了吗?所以这两个角一等, 所以三角形 e、 d、 c 全等于三角形什么 a、 e、 f 然后我们就可以证明说什么所以 a、 f 等于 e、 c 这两个角这两个边相等,还有呢, 角 a、 f、 a、 f、 e 等于角 a、 f、 e 就 等于角 c 嘛, 脚 a、 f、 e 同时又等于什么?等于等于脚 b 加上脚 f、 a、 b, 这是因为他们外角的外角的关系是不是外角和的关系,所以又因为角 c 又等于两倍的角 b 嘛, 所以就可以得到什么,就可以得到角 b 等于角 f a b 了。所以 a f 等于 f b, 所以 就可以得到 b e 等于 b 等于 f b 加上 f f e 同时等于 c, d 加上 c e 嘛。好,这道题 很有意思哈,如果说其他同学他还有其他的方法的话,可以挑战一下,在评论区写出你们的答案。好,这道题就这样子。
 00:26查看AI文稿AI文稿
00:26查看AI文稿AI文稿八上数学最难的四十八个几何模型全部吃透,逆袭班级前三。八上数学四十八个几何模型一, a 字模型、鸡爪模型,腋下两角合等于上下两角合。 八字模型,三角形中五大模型见八字除对顶,剩余的两角之合会相等。飞镖模型也叫燕尾型、双角平分线模型。三个结论完整版分享!
20小王老师爱分享










