三年级图形与几何思维导图燕子
思维导图到底好不好画?来吧,你也来试试吧。比如说这一篇文章,燕子教我们看到的内容,有序的、形象化的去呈现出来,就是思维导图了。
粉丝2951获赞1.4万
相关视频
 00:53查看AI文稿AI文稿
00:53查看AI文稿AI文稿当堂背过课文的诀窍居然是一幅图!今天光光老师带大家绘制的思维导图是语文三年级下册第二课的燕子。首先画一张喜欢的中心图,然后从四个分支进行整理,分别是外形、春景、飞行、修气。 第一条分支是外形,将特点和情感写在分支上。第二条分支是春景,将环境、植物、动物的特点写在分支上。第三条分支是飞行,飞行的姿态和动作同样写上 第四条分支是休气,将相关知识整理上就可以了。串联关键词后就能快速背过课文,快试一下吧!关关老师教你学思维导图,简单又有趣!
159青岛小博士培训 02:17
02:17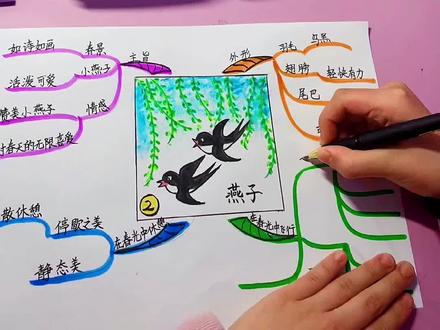 00:15查看AI文稿AI文稿
00:15查看AI文稿AI文稿有一个姑娘,她有一些任性,她还有一些嚣张。有一个姑娘,她有一些叛逆,她还有一些疯狂,没事吵吵小架。
1142语桐妈妈~ 01:12查看AI文稿AI文稿
01:12查看AI文稿AI文稿三年级第二课燕子这篇文章是著名作家正正朵写的。活泼可爱的小燕子从南方飞回来了,你对燕子了解多少呢? 一身乌黑光亮的羽毛,一对俊俏轻快的翅膀,加上剪刀式的尾巴,凑成了活泼机灵的小燕子。才下过几阵蒙蒙的细雨,微风吹拂着,千万条才展开。淡黄色的嫩艳的柳丝, 青的草堆的叶,各色鲜艳的花,都像赶集似的巨网过来,形成了光彩夺目的春天。 小燕子从南方赶来,为春光增添了许多生机。在微风中,在阳光中,燕子斜着身子在天空中略过积极的叫着,有的由这边的稻田上一转眼飞到了那边的柳树下边,有个横略过湖 面,尾尖偶尔沾了一下水面,就看到波纹一圈一圈的荡漾开去。几对燕子飞圈了,落在电线上, 蓝蓝的天空,电杆之间连着几横细线,多么像五线谱啊!停着的燕子成了音符,谱出一只正大演奏的春天的赞歌。
285艺鸣惊人 22:10查看AI文稿AI文稿
22:10查看AI文稿AI文稿结构决定性质,性质决定功能,不能上来就看数量规律,这样很浪费时间的,那图最好三十秒或者六十秒就做出来。各位小伙伴们大家好,今天这期视频的主要内容呢,是对判断推理四大板块之一的图形推理,他的知识点进行一个讲解, 同时呢以思维导图的形式进行一个串讲,能够使大家更加清晰的了解图形推理它整个一个考点和知识点的框架。 那话不多说,直接开始。图形推理呢,主要分为两个部分啊,按照题干图形的这个形式来区分,分为平面图形推理和立体图形推理。立体图形推理呢,它是三维的图形,具有长宽、高像,长方形,正方形或者说是球。然后平面图形推理呢,它是二维的,就去掉了高度,只有长宽,没有高 像长方形,正方形,然后还有圆线段等等之类的一些。然后具体的平面图形推理呢,包括五类具体的规律,数量规律、属性规律、位置规律、运算规律和特殊规律。这五大规律也不是我自己乱作出来的,而是我在我观看了市面上大部分的教徒的老师教学视频, 然后结合我自己的备考经验和考试经验得出来的这五大规律。那第一个数量规律呢,是包含这么几个点,线、面角数 和一些复合规律。复合规律主要是指前面五个结合起来的规律啊,这里呢点呢,主要是考察直直焦点,取取焦点和切点,这里重要的是一个这个切点啊,切点呢,一定是要有曲线,比方说我画一个圆,然后再画一个圆,这两个是两条曲线嘛?然后中间这个焦点是指取取切点, 然后我再画一个圆,再画一条直线,那这个就叫取直切点,切点的话一定是要有曲线在场的,那么我们在什么时候去观察,去识别这个点的数量规律呢? 当题干,图形出现多条直线或曲线相交,你看这里是不是出现了很多直线或曲线相交,那么这个时候可以考虑去计算点的数量规律。好,这是数量规律点。 再讲一下线的考察方式,主要是考察这么三种啊,直线数、曲线数和笔画数。直线数是图形线条,比方说我画一个正方形,那这个正方形它是不是就是一个简单的图形线条,它包含四条, 四条边嘛?就四条图形,然后呢就是汉字线条,这个汉字线条在图形推理呢,主要有两种方式,一个是没有加粗的,像这个填就没有加粗的,然后还有个加粗的,就是大家就能够非常的看出来,他是那种黑体字写出来的加粗的啊。 像这种就是看汉字的线条,比方说这个天字吧,有两条横线,两条横线,这个叫汉字线条。然后第三个是平行线组数,像这个正方形,它是不是就是两组平行线了?平行线组数,然后曲线数,这个比较简单,就是算曲线的数量,像圆里面这个只有一条吗?然后最后一个是计算笔画数, 主要是区分某个图形,它到底是一笔画图形或者是多笔画图形。那怎么去区分呢?主要是按照基点数来啊。什么是基点数? 就是从某个点出发,如果他出发之一条线一是不是基数?所以这个叫基点,这个设为点一吧,点一他就是基点,像这条线里面他就有两个基点嘛,所以他的基点数是二,那么他就是一笔画,那多笔画是一样的,多笔画就是基点数除以二,随便写一个哈 三角形,然后再多一条,这样一二再写一条啊,三四,他是不是四个基点,四除以二,所以这个图形呢?他就是两笔画图形, 这就是线的考察规律。那怎么去判别计算线的数量规律呢?第一题干图形出现了很多直线或者曲线,和前面的点的数量规律是一致的啊, 都是出现多条曲线或者直线相交。那么第二个是在指怎么去计算笔画数?什么时候去计算笔画数呢? 出现多端点图形,像这里这个图形是不是多端点的?或者是日字填字的变形,这个日字是作为一个图形的,整体来看 不能作为汉字线条。像这个字,正常来看,一、二三、四,他是不是四笔画?但是按照图形来算,他只能算一笔画,因为他只有两个积点,只能算一笔画,那填字他就是两笔画图形,这个是线的数量规律。 我们再来看面的啊,面的考察方式主要也有四种啊,面的数量和最大最小面。黑白块面,面的形状属性与外孔之间的关系。我随便画一个面啊, 看这里,假设这里全部都是涂黑了,这个叫黑块面,这里一共有加上黑块面是一、二、三,是不是一共有三个面,然后最大面是这个黑块面?黑块面它也有自己的性质啊,这里是个直角,它是个直角, 而且是个等腰直角,三角形黑块面啊,最大面就是这个黑块面,面的形状就是那个等腰直角。还有这里它是不是也有个四边形 与外框之间的关系呢?你看这个最大面,它与外观是相交了两条边,这个叫与外框之间的关系。 那什么时候去计算面的数量规律呢?当题干,图形的封闭面明显像这里,这个图形封闭面是非常明显的,这个时候呢,可以考虑去计算面的数量规律。 然后第四个是角的考察方式,主要是考察直角的数量,当然其他像什么锐角、钝角也可能考察, 只不过这个题目是偶尔会见到,非常少,像是某年的江速体,还是哪里会出现这种算其他角的,像锐角或者所有角的,那大部分只算这个直角,那在什么情况去算角的数量呢?第一个出现直角元素,像直角三角形啊,直角梯形等等,或者说 存在明显的垂直关系。像我画一个图形啊,这种就典型的,你看是不是分隔成了四个这个矩形, 然后这个直角数就需要去算了啊,当然一般不会出这么多直角数,应该一般是出一到两个,两到三个这种,这个是要计算角数量规律时候面临的识别的图形特征。 然后就是数的考察方式,主要包含元素的数量、元素的种类、元素的换算方法和部分数。比如说我再随便画一个哈, 你看在这里出现了一个圆,有一个球嘛,然后出现了一个三角形,那么这个元素呢?就是两个,然后元素种类一个是圆,一个三角形,它是两种啊,算换算主要是针对他可能出现一系列的图形,比如在第二个图形出现两个圆,加一个这个, 那第三个图形出现两个三角形,这样一种情况就是出题呢,想让你去计算一个三角形等于几个圆,或者是一个圆等于几个三角形,这个就叫元素换算方法。那么部分数指的就是它们相交在一起的时候,看成一个图形整理,它就叫一个部分,就叫部分数。 那我怎么在什么时候去数这个数的数量规律呢?当提纲中心由多个独立的元素组成,比方说像这里,你看是不是很独立,然后有多个这样不同的元素,这个时候就考虑计算数的数量规律。 那最后一个是复合规律,复合规律呢,指的就是前面点、线、面、角数所有的综合起来考察,比如说这里点与点、点与线,或点与面、线与面等等等等,这是复合规律。当然万变不离其中啊,它还是和前面的数量规律是归在一起的。 我们再来看第二大类的规律,是属性规律,主要包含三种啊,三种对称性、曲直性和开闭性。 对称器主要是考察轴对称、中心对称,那轴对称,这就比较简单啊,比如说我随便画一个三角形,那这个就是它的对称轴了,它是不是对称轴图形,它的方向和数量这个方向呢?主要是也是给出一列图形, 比如说第一个是数值吗?第二个就是向顺时针转四十五度,第三个就可能是平的,再转四十五度,那数量呢?第一个是一条,那第二个两条,第三个可能就是三条,这个是对称轴的数量。 那第三种就是考察对称轴和图形点、线面之间的关系。比方说这个对称轴将这个图形是不是过了点啊?是过一个点,然后过一个面和线呢?它是和线有交点,这就叫对称轴和图形点线面之间的关系。 那第四个多个对称图形拼和对称轴之间的关系,这什么意思?比方说我画两个三角形啊,你看这也是一个对称轴,这是个对称轴,说明他们两个对称轴,它是平行的,这个就叫对称轴之间的关系,当然也有可能垂直。那什么时候看出对称的属性规律呢? 当多个图形明显对称,可通过一条轴线折叠中刻或者旋转一百八十度,就可以考虑看到他的对称的属性规律, 这个是对称的属性规律。然后第二个是取值,取值的考察方式就是纯直线、纯曲线或者曲线混合图形和前面的这个曲线交点和直线交点是差不多的。这个图形识别特征啊,都是出现了明显的圆弧或者全曲线图等等啊。 然后第三个,第三个图形规律是指开闭考察方式主要是考察全封闭、全开放或是半开放、半封闭。我举个例子啊,像这个三角形,他就是没有开放的,这里面和这里面是完全隔绝的,这个叫全封闭。那什么是全开放呢?比方我这三角形是不是隔了一个,他就要全开放图形, 那什么是半开半闭呢?这也是个缺口嘛。那我在这里加条线,你看这里它既有这个什么封闭图形,然后又有开放图形,这个就叫半开放半封闭图形,那怎么去识别它呢?当出现生活化线条或者出现条时候,且没有明显其他个规律, 就是说这个开闭的属性规律是要在其他规律全部试完之后,我们再去试这个规律,这个叫属性规律的开闭规律。 我们再来看位置规律。位置规律主要有四个啊,第一个是平移,第二个旋转,第三个翻转,第四个是图形间的关系。那平移呢?就包括移动方向、移动步数,移动步数到底是恒定的,就都是移动一步,或是递增的一二,或是递减的三二一。这种和前面的对称轴的 旋转移动规律,它是相类似的啊,相类似的。然后图形特征呢,主要是当图形的组成元素基本相同,可以通过元素的平移,上下左右平移找到下一个图形,也是给一组嘛,然后在这个问号在下面 a、 b、 c、 d 四个里面选一个,就是平移的位置规律。 然后第二个是旋转的位置规律。考场方式呢?旋转角度四十度、九十度、一百三十五度,旋转方向是顺时针、逆时针。 那怎么去识别呢?也是组成相同,然后通过旋转可以得到下一个图形。然后第三个规律是翻转规律,主要包括左右翻转和上下翻转。左右翻转就是在中间画一个对称轴嘛,然后上下翻转是上下翻过来对称的图形的呢,也是元素相同,明显镜像通过元素的翻转可以得到下一个图形。 再来看图形间的关系,它是怎么一个考察方式,主要是考察图形的相邻相切和相交相邻呢?大概画一下这两个圆,它就是相邻的 相切呢,就这两个圆,有个切点,有个相切的相交呢?这个比较简单了哈,算交点了,两个交点它是相交的,然后相交它有两个比较明显的区分方式啊, 相交于边或者相交于面,相交于边主要是指相切哈,相切,这里再画一个,你看相交于边,这个边是不是大家的公共边,这个边是不是相交在一条边?只有相交一条边可能在某个图形里面呢?像在这种图形里面, 它和它相交,相交到两条边了,但图形画的可能比较丑啊,大家只要知道这个香蕉边的数量和样式,知道这个规律就行了。然后第二个就是相交于面,比如这里相交于面,这个相交于两个面,然后这个面积呢, 主要是在一些方块里面可能会出现这个面积的计算,这里可能会出现面积的计算,这个叫图形间关系。相交的关系,那么怎么去识别呢?当出现圆或者直线存在切点的时候,可以考虑图形间的关系。 那我们接着来讲运算规律,什么叫运算规律?当我们看到出现九宫格的时候,当出现这种呢,一般就是考运算规律,加减同异或者是黑白运算。那么加减同异呢?主要有这么几个 方向,主要是考察去同存异就去掉相同元素,或是去异存同去掉不同元素,保留相同元素,或者直接叠加在一起。那图形特征呢?是元素组成基本相似啊,相似,然后有相同的线条同步出现, 然后接下来一个是黑白运算,黑白运算呢,大体和价钱同意,他是同归属在一个运算规律里面,只不过黑白运算他更可能是偏向于那种颜色,就是黑白怪的考察。 图形识别特征呢,是当图形出现,图形分割、颜色填充、轮廓相同或者变化无序的时候,可以考虑黑白运算。当黑白运算需要注意一个点哈,就是我们得出来的规律一定要经过计算,比方说在某一个题里面黑加黑,他得到的是黑,但在另外一个图形里面,他可能得到就是白。 所以我们一定要进行运算,一般是先横行计算啊,在那个九宫格里面先横行接着横行,不行我们再竖行,一定要经过验证 才能证明我们这个黑白运算的规律是在这一幅图里面是成立的,这个是运算规律,我们再看特殊规律,当然这个特殊规律是我自己随便弄的啊,便利和功能元素,因为我们可以看到这个特殊规律其实就是前面四种规律的一个结合体。 我们看便利啊,便利是不是元素的增减,那这个元素是不是前面的数量规律数?同样的啊,我们看到功能元素,它也是这样子, 它是包含这个小点、小圈和小箭头,同样的和前面的算数是类似的,只不过这里可能它空元素更趋向于这个标记,比如说标记位置,我画一个三角形,画一个直角,三角形, 这是直角哈,然后我这里标记一个黑点,说明这个点一定是跟随这个直角,说明我们这个角呢,在后面的图形也要去关注到。然后第二个是标记移动轨迹,什么叫标记移动轨迹?然后在第一个图形, 这个小白球是在左上角,然后第二个图形呢,是在右上角,这个就标记移动轨迹,他是在顺时针走吗?而且是走一步。然后第三个是标记点,连线和图形之间的关系,这呢是出现两个标记点,我们那个图形中啊,他自己里面有很多这个线条啊, 然后这里标记一个点,这个标记点,这个在连线,是不是和图形之中的这个虚线或者实线,它是平行的,这个叫标记点,连线和图形之间的关系。然后第四个这个考点是比较新奇的,好像是在二五年的天津卷应该是出现过, 比方说我这里画一个三角形嘛,这里标记个点,这个点发出的直线数是两条,有点像算那个记点数是一致的,他是发出的直线数是两条,当然他有可能发出那个曲线,具体是要按照题目的图形来安排的。 好的,这就是所有的平面图形涉及到的规律。但有的同学可能会问,老师,你这规律这么多,你看你看这么多,我怎么去记?大家不要着急,我教给大家一个好用的比较直观的方法来记哈。 那么记忆的原则主要是按照这么一句话,结构决定性质,性质决定功能。那怎么去解释呢?我就按照拿我们的平面图形这五大类的规律来解释一下啊。 首先这个数量规律是不是指图形的基本构成点心面角数嘛?对不对?点心面角数是组成元素,是组成图形的最基本结构,特别是点啊,点是最小的,然后不同的点连起来就是构成了线, 然后不同的这个线围成的那个封闭空间是不是就叫做面?然后角也是一样的,角就是从一个点发出两条射线,那这个就叫做角。那数就更简单,它就是点心、面角它构成的这么一部分元素。所以说点心面角数它的数量规律呢,是构成图形的最最基本规律, 这个就是叫做结构,然后结构决定性质呢?性质就指属性嘛,就指图形的属性,像这个属性是包括对称、取值、开闭,然后性质决定功能。功能是不是某个事物要对其他的事物产生作用,这功能就是作用嘛,比如说我用手机是用来上网的,那上网就是手机的功能。 那在发挥功能之前,单个图形它的位置是不是要发生改变,发生移动,或者是各种交换等等之类的一些位置上的规律, 然后再和其他的图形进行一个计算。前面这三个呢,是单个的图形自己内部之间的这个规律,然后计算呢,是至少两个及两个以上的图形之间的规律,那这个就比较容易记了,结构决定性质,性质决定它这个计算的功能。 然后除此之外还有一些特殊规律。当然这个特殊规律我刚刚已经讲了,我这里是便利还有一个功能元素,但其实变量、功能元素都是前面四种规律的一个变形题。因为我们知道在国考的十道这个图形推理题中呢,每年总会有那么一两道是创新题,就是一眼咱们大家看不出来的。 那么这个时候呢,他就可以被归为到这个特殊规律里面,我教大家怎么去对付这种题目哈?怎么去对付?我们首先是要按照我们这个规则来,结构决定性质,性质决定功能,但是我们不能直接去看它的结构啊,那个太麻烦了。你看我们的数量规律,这里有直接四十九个点, 但是看我们这个预算规律,是不是只有十九个点,几乎是最少的?那我们就需要从事物的外部去看到事物的内部。什么叫从事物的外部看事物内容?因为我们知道事物的本质啊, 他是很难去认知的,他是不容易去认知的。所以我们看东西,比如说看一个人是不是先从他的外貌,从他的穿搭开始看,然后再去看到他的这个心灵或是本质呢? 做图形,做平面图形推理,他是一样的道理,通通的去看外表就行了。先看外表,比如说从第四个开始看啊,从计算规律,再看到位置规律,再看到属性规律,最后再去看点心面角数的数量规律。这个就是咱们做题的一个逻辑,做题的时候一定要按照这个逻辑来, 而不是按照其他逻辑。你不能上来就看数量规律,这样很浪费时间的,因为我们时间压力是比较大的嘛,那图子就要三十秒或者六十秒就做出来,如果在图子里面一道题目你花了两三分钟,你花在其他板块的时间就会变得非常紧张了,所以那是不建议的,就是按照这个从下往上去做题。 虽然我们认识规律是从上往下,从本质开始吗?但是做题还是从外表开始,这个是平面图形推理的这样一种记忆和理解的规律。还有这个规则,结构决定性质,决定功能。 那同样的立体图形推理呢?也是按照这么一个规律,结构决定性质,性质决定功能。分为多面形构,是不是结构了,是不是结构。因为立体拼合它是由一组一组这个立体图形搞在一起,它就是呃,图形和图形之间的关系, 拼起来重构嘛,就类似于立体的重构。然后接下来就是洁面图,是一个完整的立体,然后给他砍一刀去识别他这个洁面。然后是图类呢,就是看整个立体的它一个外表的轮廓是什么样子。那具体来讲一下多面重构呢?特征主要是这么两个哈, 要么题目会给出一个多媒体平面展开图,要求从四个选项选出这个立体图形,或者呢给出一个立体图形,要求选出对应的展开图。常见多面体包含这个两种,一个是六面体,一个是四面体或者八面体。还有其他什么不规则多媒体,乱七八糟的一些, 我们只要核心掌握六面体就行了,因为掌握这个六面体,顺带就会学会了四面体和八面体,这是很容易去迁移的。那么六面的解决方法呢?最常考的有这么几种啊,相对面的排除,整个相对面。比方说我画一个六面体的这个视域图啊,大家画的不怎么好啊, 你看这个面和这个面,这 z 字面它就是相对面,然后隔音面,这个面和这个面它是相对面,这个是相对面,这个是我们的核心排除法,我们根据选项来排除嘛,就是核心排除,然后 第二个是公共编法,比如说这个面和这个面这两条编的特征有没有对应啊?这个也是核心的排除法,那么这个箭头法就是做一个介绍,限于时间关系啊,我这里不做一个详细的介绍,就简单介绍的,就找一个特殊面,比如说这个面这里画个箭头,然后根据这个箭头的这几个相对面相对编吗?相邻编 就可以到脑海中给他拼一下,还是比较考验考生的这个空间重组能力的。这个箭头法是需要去简单的掌握一下的。 那同样的四面体和八面体,还有其他不规则多面体,通通都是六面体重构的变形形式。解题方法基本上是按照前面三个,只不过这里多了一个画编法,当然画编法和箭头法是类似的一个比较简单的易懂的这个判别法,这是多面体重构考点。 我们再来看立体拼合,主要题目呢,会给出一组立体图形的分解图,然后判断是不是两个凹凸互补吗? 凹进去的和凸的,他必须要两个要补在一起,这叫凹凸互补。然后数量守恒,主要是一些这样什么出现了很多正方小方块的, 那么这个数量拼前和拼后,他们数量要保持一致,这个叫数量守恒原则。那第三个考点是洁面图题目,给出一个例子图形,然后找出哪个是他可能的洁面主要是用刀去砍他,那核心原则呢?洁面一定是一个平面图形,这个不用多说嘛,因为刀他不可能是弯曲的, 他有可能有曲线,但是他一定不会是那种三维图形,他一定是个二维图形,平面图形嘛,然后前面是封闭的嘛? 对,还是比较容易理解。然后刀面延伸原则就是我们砍了这一块,不能只看这一块,因为他会延伸到其他部分,这个叫刀面延伸原则。要解决思路呢,主要是进行一个排除,反向排除, 然后要掌握基础几何体的洁面,比方说正方体有六个面嘛,我在这里面砍一刀,他最多只能砍到六边形,因为他只有六个面,最多只能砍到六边形。这是比较一个基础的几何体洁面的一个形式吧,大家要去熟练掌握。 然后最后一个就是仕途类,这个仕途类在我们之前的这个小学或者初中还有高中这个学阶段已经掌握了。三式图嘛,正式图、左式图,这三式图当然在公考的题目中呢, 其他几个式图像仰视图、右视图和后视图都会考到。题型特征主要有两个,已知立体图形,选择式或者是已知三式图呢,去判断立体图形或者是其他的组成方块数。 那解决技巧也主要有两个哈,也是轮廓法。轮廓法说白了就是硬看,因为我们的基础知识在这里啊,你硬看大部分题目是可以看出来他不会出的,很难。第二个原则是虚实线原则,这里的虚实线原则和我们之前接触到的可能会不太一样,因为在我们之前学习,是不是在没看到的这个线,是不是要标虚线, 但是在公考题目中,这个虚线就行了,标出实线来说明这个题目他没有这个太多的错误, 如果他没有标虚线,我们不能认为他是错的,因为在空号题目他不标虚线,他也是对的啊,所以在这组要注意到这一点,那这里呢就是所有的图形推理的整个考点,整个知识点框架,希望这期视频能给大家一个更好的帮助,谢谢。
44我心志翔
猜你喜欢
最新视频
- 1564草包1号














