师傅,咱们到通天河了,过了这通天河,咱们就离取真经不远了。猴哥,这河这么宽,哪过得去啊,咱们不如去找户人家化点斋饭呐。 呆,你这呆子要不要吃猪耳朵啊?看不到那边的石碑吗?走吧,师傅,咱们过去看看那石碑上写的啥。遇过此河须知河宽卷等三角,可解其难。悟空 这是何意啊?师傅,这石碑让咱们求出通天河宽是多少?啥是第八届,你们照看好师傅,老孙去去就来。 这通天河果真好宽呐,可无法直接亮出河宽,该如何求出这距离呢? 这河宽该如何求?大圣,我来助你是土地公啊,你可知这通天河河宽多少?小仙不知,但是小仙有本解题秘籍要送给大圣。什么解题秘籍?哈哈,大圣且拿去仔细观看。 小仙去也,这老头走的倒快,且让俺老孙看看通天河之谜。 俺老俺老孙明白了!证明俺老孙明白了 俺老孙明白了。证明线段相俺老孙明白了。证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决。哈哈哈, 这全等三角还真有意思,这通天河宽我能求出来了,且随俺老孙来看看。 这通天河之谜乃是我毕生所学,没想到大圣不过短短一刻钟就破解了我的问题,只是我还有一事相求,老人家尽管说来, 我这大徒弟无所不能。我一生酷爱数学,只可惜不够精通,听说在公元二零二六年,我这谜题小孩子都能破解,我想请大圣帮我去看看那个世界,回来讲与我听听。 这有何难?俺老孙可是齐天大圣,你们且安心过河,俺老孙去去就来! 这题我会判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等,解题时要根据已知条件的位置来考虑,只具备边边角时,是不能判定三角形全等的。 今天这堂课真是令我大开眼界,原来几千年后的世界是这样学习知识的,比俺老孙的七十二变还要厉害,也不知这几千年来是如何一个过程,不然俺老孙回去还可以讲给老龟听听。
粉丝7获赞168
相关视频
 05:10查看AI文稿AI文稿
05:10查看AI文稿AI文稿开始,好,我们今天要把这个角角边啊,当成我们三角形指规作图的最后一个内容啊,我们去看一下角角边, 那我们这两个角呢?一个角设成 a 法,一个角设成 beta, 另外一个角啊?另外一个边我们设成 a, 我们这写上角角边, 我们之前就说过这个角角边的问题,是吧?角角边的时候,我们去我们先看一下啊,那我们的一个角 a f a, 假装我们坐这儿,那我们再来一个什么角角边,那是不是要在这儿做一个角?但是我们会发现等 于贝塔的这个角是不是有无数个?看这是不是可以有一个,那我们把这根线如果给他延长的话,这是不是也有一个贝塔?这是不是也有一个贝塔?那我的角角边,哎,我们会发现了角角边,是不是这个画起来非常难画? 那我们在这呢,我们去考虑一个问题啊,怎么办呢?我们的三角形的内角和 等于一百八十度,那我们知道了两个内角之后的话,第三个角我们可以用 gamma 来表示, 那伽马就等于什么了?等于一百八十度减尔法,减贝塔,那我们的这个伽马该怎么去画啊?我们是不是可以考虑一下把尔法贝塔 踏放在同一条直线上面,是吧?那我们的尔法和贝塔放在同一条直线上面,一个是尔法,一个是贝塔,那剩下的那个是不是就是伽玛了? 因为我们三角形的内角和一百八十度是不是和一根直线的平角是正好吻合的,对吧?好,此时我们怎么办呢?我们先在图上面做一个耳法, 哎,我们先画一个 alpha 啊, 好,我们的 a 法这有了, 那我们刚才说什么来着?我们是不是说要再做一个 gamma, 是吧?好啦,我们在同样下面的位置啊,我们刚才把刚才的这个阿尔法重给它画一个, 我们这个用的是什么啊?用的是将我们的角给他去平移,哎,我们在这个位置 beta 的这个位置也画一个,那我们把这个 alpha 的角弧度量一下。 好,阿尔法有了, beta 呢?记不记得我们在第二章做这个尺规做角的时候啊?做两个角怎么办呢?这儿是不是阿尔法?嗯,那 beta 是不是在这个位置?哎,好啦, 那我们是不是就会得到了啊?这个角度就是尔法, 这个角度就是 beta, 那生下的这个角自然而然就是 高尔马了,这个高尔马是不等于一百八十度减阿尔法减贝塔。那我们现在是不是就把这个角角的另外一个角转化到了这个三角形里面了?那我们刚才说是不是这个是角角边那边是不是也是确定的呀? 那我们去量一下这个边啊,是不是转化到了这个位置,我们去量一下这个,哎,这个边有了,好嘞,我们把它搁这,那,这是不是就是 a 呀? 画一步标一步,以防忘记了,那角角边有了,那这个伽马应该放哪呢?是不是应该放到这个位置上, 是吧?哎,别忘了啊,那我们一样的啊,只会做图,我们做一个大大的蛤蟆,你看这个蛤蟆的角度非常大啊,那我们也尽量给它画大一点,然后我们再量取这个弧度。 哎,注意,在这量的时候,我们是不是一个焦点的边在这边看啊,一个在哪?哪个地方?在这个地方。哎,所以呢?这个焦点和这个顶点的连线就是我们的一个 伽马,哎,这个位置就是我们的伽马吧?那么我们的贝塔到哪了?是不是贝塔自然而然就到这了, 这是不是画出来了?那么我们的角角边是不是其实转化成了什么?边角?边角来去转化的,明白了没?嗯, ok。
60安迪倩 01:41查看AI文稿AI文稿
01:41查看AI文稿AI文稿这个视频我来讲讲。用齿规做角,比如已知一个角 a o b, 只有圆规和没有刻度的直尺,如何做出一个和它相等的角呢? 嘿嘿,要做角,先得有条边,拿直尺画一条边,记做射线 o 一片 a 一片角,有两条边,那还得再来一条。不过这一条就不能这么随意了,咋画呢? 步骤有点多,你可得听仔细喽。首先,在已知角上以 o 为圆心,以任意长为半径,画一段弧,交他于 c, 交他于 d。 接着把圆规挪过来,以 o 一撇为圆心,还是以刚才的长度为半径,再画弧交 o 一撇, a 一撇与 c 撇点,此时 c 一撇就对应这边的 c。 那我只要再找到对应这个地点的 d 撇点, 就能确定另一条边了。接下来,我就教你如何去找这个 d 撇点。用圆规量一下 cd 的距离,保持圆规不要动过来。在这边以 cd 撇为圆心,再画一段弧, 发觉没,第一撇点肯定记在这段弧上,也在这段弧上,那显然这个焦点就是第一撇。把 o 一撇,第一撇连起来做射线 o 一撇, b 一撇,那这个角就等于已知的角 a o b 啦。 好了,再回顾一下刚才的过程,做一个角等于已知角时,一共有三步,首先随便画出角的一条边,接着分别过角的顶点,做两段一样的弧。 最后用圆规亮出焦点距离,再做一段弧,有了这个焦点,就能做出角了。怎么样,明白了吗?明白的话就动手试试吧!
814爱学习 02:40查看AI文稿AI文稿
02:40查看AI文稿AI文稿哈喽,全等三角形尺规做图,那今天画已知一个三角形 abc, 我们要画一个三角形 a 撇, b 撇, c 撇,使他们的三边分别和已知三角形的三边相等。那首先第一步呢, 我们需要画 b 皮, c 皮等于 b c, 就是你任选一边先画上, 那画这个呢,做一条线段等于已知线段呢?我们需要先画一条射线, 然后把这个点呢记做必品,然后拿出我们的圆规, 圆规,然后来量一下这个 bc 的长度, 然后呢把圆规的固定的这个角放在这个壁点上,然后这样画一个壶,那这个壶和这个射线的焦点就是我们想要的那个 cp。 第二步,我们需要以这个 b 撇和 c 撇为圆心,以线段 ab 和 ac 长为半径画胡, 那以 ab 为半径画壶。那首先我们需要量一下 ab 的长, 然后呢把圆规的还是一个角放在 b 撇这画胡,然后呢再量一下 ca 的长度, 量一下 ca 的长度,然后呢再把圆规的这个角放在 c 撇上, 然后和刚才的壶会有一个焦点,两壶香蕉与点 at, 这样的话三角形的三个顶点就找到了。那下一步我们就是拿直尺去连接线段 a 撇、 b 撇 和线段 a 片 c 片, 这样就画好了。
306豆豆数学mathDRW 09:53查看AI文稿AI文稿
09:53查看AI文稿AI文稿好,咱们来学习啊,做,用指规来做一个作图。问题就是知道了三角形啊,这个 a b c, 嗯,然后咱们做一个新的三角形, a 撇 b 撇 c 撇,就是绿色的,这个使得呢,这个 a 撇 b 撇等于 a b, 角 a p 等于角 a a p c, 嗯, a p c p 等于 a c。 那这个指挥作图怎么做呢?咱们现在来说一下。先图实话,嗯,从这个地方开始, 我制作成了这个啊,可以模仿 ppt 的分布影视啊,可以点下一步,下一步就 ok 了, 你可以点上一步,回头看上一步的过程。点动画演绎,那就是连续的把咱们所有的动作连贯起来, 一般咱们,嗯,说这个问题的时候,应该用这个按钮,下一步, 嗯,就在平面上,嗯,做出了这个点 a p 的有角的顶点 a p, 我任意起的。然后呢,过 a p, 先画一条色线啊,看看, 下一步,直指放上来。过 a 啊,画一条射线,画完直指周啊,恢复原来的位置,这时候得到一条射线, 这个时候呢,咱们先做角 ap 出来先,好不好啊?先做角 ap 等于角 a, 这时候呢,用用圆规来做, 先把这个圆规呢放到 a 和 b 之间,嗯,当然圆规的半径是可以任意放的,嗯,适当就可以了。 然后就画一个弧,呃,那这条弧呢,他就和 a c 交于点,按和 a b 加一点点。画完了,这个就要把圆规啊放回到 ap 这个地方了,半径就不要不要变了啊,半径不要变,直接平移下来, 平移下来画出一个同样的弧,这个弧呢,他就和刚才射线 apd 有个交点 f 了,这时候呢,圆规又回到这个点,哎, 不是到 b 啊,到这个点 m 来截取这个 m m 的长度的,但是要有一个做图痕迹,要画出这个短的弧,再下来,以 f 为圆心,以同样 长的半径画个弧度,有一个交点,这时候圆规先放过边了,直指又来了,经过 a 撇距而放直指, 再画一条线,线,射线,食指画完又收回来,这时候呢,这个角 ap 啊,就是角这个, 那这个 e a 撇 b, 它就等于角 a 啦,已经 还要画呢, a 撇 b 撇等于 a b, 这时候呢,咱们下一步就用圆规来了,来截取这个 a b 的长度,然后呢,画 一个啊,这个指规的一个作图痕迹吧。然后呢,再把圆规放下来,半径呢啊,不要变。 再画出同样的一条短的弧,两个弧呢,它的半径是一样的,得到点 b 撇了,那么 ab 撇,就等于 ab 了, 然后这时候你圆规知足,又放到 ac 那里去了吧, 画一条短的弧,就是在这那个地方画一个作图痕迹啊,用虚线,然后这时候又放到 a 撇这里,然后呢,又来画 短的弧,它就和 a 撇 e 呃,有一个交底的 v c p ga, 一撇 c 撇就等于 ac 了,因为圆规同圆的半径相等下来,圆规不用等一下,要框住这个三角形出来,所以直指再用一次,再用一次, 把这个直指放到这个 b 一撇 c 撇这里, 这支笔出现以后,咱可以画出这条线啊,这样绿色的三边都连起来了,然后呢,咱到下 这个食指就放回原处,这时候画出来的东西啊,这个绿的和这个黄色的两个能不能重合呢? 咱们就用这个点这个按钮, s a s 按钮,那就过来看看能不能完全重叠。 ok, 发现了这两个字他都能够完全重叠的, 这个 c 品摊合这个点 c 也成别了。这样,那如果复位 点这个按钮,点这个边角边这个热文字按钮,那就移动过来验证一下。然后咱们就发现了一个公认的事实,这就所谓的 s a e s 边角边公里 就得到全等三角形的一个判定定理。如果两边以及这两边的夹角把它对应相等的两个三角形,它是全等的, 因为刚才指挥作图啊,作图的这两个能够重合。嗯,如果点这个动画按钮,就把刚才咱们 做图的过程呢连贯起来,大家看一下效果,这时候鼠标不用动,它会自动播放, 还有一个要连接起来。 好,那这样咱画好也可以验证一下。发现了啥?发 现了一个全等三角形的判定公里,就是 sas 这个判定的定公里 在书上,现在中学课本的书是作为宫里出现的,但是在欧基里德老先生的啊,名著里面就是几盒,原本里面他不是宫里的,咱为了照顾啊 这个青少年,他的那个灵敏阶段啊,思维啊没有发展,但像数学家这么高的层次,有谁都为了降低这个教学要求就搞成了公里的形 是, 那用这个呃课件就可以很好的演绎所谓的边角边公里。 想学几何画板的老师可以关注咱们这个号,订购几何画板培训的精品专栏, 专栏的名称是数学案例以及画板动画制作。感谢大家的支持,再见。
47初中数学苑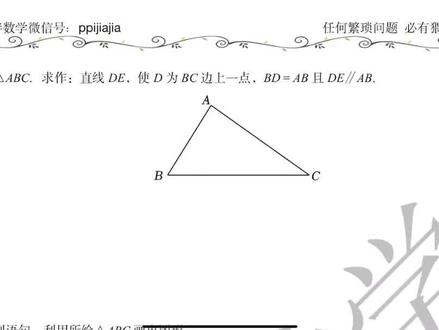 04:13查看AI文稿AI文稿
04:13查看AI文稿AI文稿八、上必考指规作图一、平行线的做法指规作图中相对说比较复杂的题目,该如何做到?那第一个呢?我们来先考虑一下如何画平行线, 大家可以读题,在三角形 a、 b、 c 中呢?我们做一条直线 d、 e, 使得什么呢?使得 d 为 b c 上的一个点,然后呢, b、 d 呢?等于 a、 b, 并且 d、 e 是平行于 a、 b 的, 那我们知道大概图形呢?应该长什么呢?长的是这样一条平行线。那平行线在我们指位做图里面该如何去做呢?这要给大家去做,说一下他的一个方法。 做平线呢,主要是通过什么呢?通过构造全等,构造全等,构造全等呢?利用什么呢?利用同位角的知识, 利用同位角相等他们的一个知识来证明出他们的一个平行。那如何构造呢?我们来看一下这道题,他说什么呢? b、 d 是等于一个 ab 的 bd, 等于 ab 呢?比较简单直接,拿什么呢? b 点为圆心, ab 长度为半径,做圆弧即可,我们可以得到什么呢?得到一点 d, 而此时呢,这个点地就是我们所要求的点地。那如何做一个 d、 e 平行于 a、 b 呢?注意了,我们需要构造什么呢?构造一个全等的图形,就比如说我们现在呢, a、 b、 d 已经是一个三角形了,要想证明一个平行关系呢?我们需要构造什么呢?构造一个三角形,比如说使得这个角一等于这个角 b, 而且这个三角形呢?应该是什么呢?和我们的 a、 b、 d 是个全等的关系,我们只要去构造这样的一个全等三角形,就可以利用同一角相等的知识来证明他们的平行道,那构造的方式是什么呢?全等该如何构造呢?利用的是我们边边边的一个证明方式, 那具体做法是怎么样呢?我们可以考虑怎么样呢?也第一步,以地点为圆心 以地点为圆心怎么样呢?以 b、 d 长为半径 怎么样呢?画弧,我们的目标是什么呢?通过这样的画弧,我们可以得到一个什么呢?得到一个 d, e 是等于一个 b, d 的 d 呢?是等于 b d 呢?相当于有一条边已经相等了,接下来呢,我们要靠什么呢?靠证明另外两条边也是相等的关系。 那此时呢,我们知道这道题里面比较巧的是 a、 b 已经等于我们的 b、 d 了,所以我们在求 e 的过程中,刚开始是画的一条弧,已经得到了一点, 那现在呢,关键就是 f 点应该如何确认呢? f 点确认的方式是什么呢?是以 d a 长度 d a 呢?是等于什么呢?等于 e f 的,所以是以 d a 长度为半径做的圆弧。那如何做呢?第二步,就应该是以 e 为圆心, 以 e 为圆心,而我们的 d a 长为半径 画弧,那画出来结果是什么呢?就相当于是一个这样的一个圆弧,他们交易什么呢?和刚才这个地点为圆心画圆弧,交易点 f, 那此时 f 就是我们所求的这个点。那我们第三步呢?连接我们的 e、 f, 那我们可以通过什么呢?三角形 a、 b、 d 是全等于三角形 f d、 e 的, 通过边边边的形式来证明,说明你全等,所以角一呢,就应该是等于角 b 的,角一等于角 b, 所以呢,两条直线就是平行的,我们只需要做什么呢?做一个延长即可。 那这就是我们的平行线的一个画法,通过构造 s, s, s 的全等来证明出它们的运行。
247胖胖数学 06:28查看AI文稿AI文稿
06:28查看AI文稿AI文稿今天我们来讲一下这个构造全等三角形的方法, 这是涉及到的比较常见的一种,就是利用小平衡线和垂线来构造全等三角形,这个往往也是我们呃构造辅助线的一个常常用的一个考点。 关于这种题目,就是说在出现了小平分线和垂线的时候呢,我们一般是通过延长垂线, 然后利用小脚边的这种方法来进行两个全等三角形判定,从而解决我们的一个题目。 呃,你看一下题目,这个如图,在三角形 a、 b、 c 中, b 一 是角平分线, ok, 这个根据条件我们可以找出一个信息, b 一 为角平分线,那我们做一个标注, 然后 a、 d 垂直于 b 一, 现在垂足为 d, 要注明角二等于角一加上角 c, 那 这种我们就可以通过构造 一个旋转三角形的之路来进行证明 整个助名。好,我们继续写一下,嗯,过线段 a、 d 给它进行延长,交 b c 于 f, 这样做一个辅助线, 这里是 f 点,然后因为 b e, 为什么呢?这里是交平分线, 所以这里我们可以得出就有角 a b 的 等于角 f b 的, 然后有一个角平分线的性质, 也就是说与角平分线 到平分线上的一个点到两边的距离相等,我们有这个性质, 两边的距离相等, 所以我们就可以知道 df 是 等于 a、 d 的, 嗯,同时还有什么呢?这里的这里的这个 a、 d, 而延长之后就是 af 是 垂直于 b、 e 的, 嗯,同时它是一个角平分线, 这里的 a、 f 垂直于 b、 d 啊,所以这个角 f 的 b 是 等于角 a 的 b 等于九十度。 ok, 嗯,这样的话我们就可以得出一个信息了。三、 三角形 b 的 f 和三角形 b 的 a 中, 我们可以根据前面得出的第一个两个三个信息, 有三角形 b 的 f 是 全等于三角形 b 的 a 的, 这里就可以说明是角角边的一个判定条件。 ok, 呃,根据这个判定条件呢,我们就可以知道 角二可以等于角 e、 f 的, 所以我们可以得出这个信息。然后,呃,不,由于 角 e、 f 的是三角形 a、 c、 f 的 外角, 所以我们根据内外角的一个性质就可以得出角 b、 f 的是等于角一加上角 c 的, 角二 是等于角一加上角 c, 所以 我们就可以证明出来了。这个呢,就是我们在利用角平分线和垂线来构造全等三角形的一个答题方法。
32健康小哥 03:19
03:19
猜你喜欢
- 2958车轨质检员


![八上数学:全等三角形的判定-角边角(ASA) 八年级上册第一单元,全等三角形是八上的一个难点,这个视频适合孩子预习,也特别适合家长和孩子一起学习,也适合在学校学完觉得理解的不透彻,再看史老师的视频巩固知识点#初中数学[话题]# #全等三角形教学 [话题]# #图形与几何[话题]#初二数学 #全等三角形的判定](https://p3-pc-sign.douyinpic.com/tos-cn-p-0015/oYAvBBbSEEnC57nI2T3fCF7bsD20TeIfsmaVRA~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2082182400&x-signature=L9ZKc5vb1%2F00je0%2Be%2BzgzdFpn68%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251227165439AFD115FF76C6AC8AE519)








