6年级上册数学几何奥数
去呐喊春在大地,啦啦啦啦啦啦啊。哎呦我去。 嗯, amazing。
粉丝37.3万获赞141.4万
相关视频
 03:18查看AI文稿AI文稿
03:18查看AI文稿AI文稿今天给大家分享一道六年级上册思维题,外圆内方与外方内圆来看题。 如果图一中外圆的半径是两分米,那么圆内大正方形的面积是多少平方分米?我们来先来解决第一个问题,它要求 圆内大正方形的面积,它告诉我外圆的半径是两分米。来看外圆跟正方形有什么关系呢? 我们知道外圆的这个直径呢,等于正方形的对角线的长度,那我要求正方形的面积,我们可以用一个公式,正方形的面积等于对角线 乘对角线除以二,那这条对角线的长度是几呢?相当于圆的直径等于二乘二等于四, 二乘二等于四,算出它对角线的长度是四,那我用这个公式四乘四除以二,算出正方形的面积就等于 八,所以圆内大正方形的面积是八平方分米。接着我来看一下第二个问题,如果图二中外面正方形的面积是十二平方分米, 那么内圆的面积是多少平方分米?来观察圆跟正方形有什么关系呢? 这条是圆的直径,圆的直径跟正方形的边长是一样的,我们可以把正方形的边长用二二来表示, 这个是二二。题目告诉我正方形的面积是十二平方分米,正方形的面积等于边长乘边长,那就是二。二乘二二等于十二,二二乘二等于四,二的平方等于十二 二的平方呢,就等于十二除以四等于三。要求圆的面积。我们知道圆的面积公式是等于 派二的平方,我们已经知道二的平方等于三,现在呢,我们只要用三点一四乘二的平方三就可以了,等于九点四二平方分米, 这个是八平方分米,写个单位,这个是四分米。 第二个问,算出内圆的这一个面积呢?是九点四二 平方分米。同学们,这道外圆内方与外方内圆的题,你学会了吗?
13思思老师 00:28
00:28 01:54查看AI文稿AI文稿
01:54查看AI文稿AI文稿今天还是风台六上的期末考试题,快来看看吧!图中阴影部分的面积占空白部分面积的几分之几。好简短的一道题图在这里 想知道阴影占空白的几分之几分别把空白和阴影都求出来呗。空白的, 哎呀,这是一二三四五六七七个完全一样的,想求七个,先把一个求出来。既然最终我只求面积比,这里面的半径就随便我设了,设一个最好求的数, 我设其中一个小圆的半径为一,那么空白的部分是七个。这样的小圆每一个面积都是 pi r 方,也就是 pi 乘一的平方来七个,所以是七 派,不用着急算啊。最后我们要求面积比的,那阴影部分呢?阴影部分不规则没关系,遇到不规则的图形,咱们就那么两个思路,要么胳膊,要么整体剪空白。 这道题的整体是一个大圆,空白是七个小圆,非常简单,所以咱们只要把整体的面积求出来,空白的再一剪掉就 ok 了。 整体的面积我得知道大圆的半径,既然小圆的半径是一,那么大圆的半径应该就是三, 所以说这个大圆面积应该是派乘三的平方,再减去空白部分的。刚算完是七派,也就是九派,减七派等于二派, 各自的面积都求出来了。我要算的是阴影占空白,那么应该是几分之几呢?老规矩,打在评论区哦!
11奥数章鱼姐 00:18
00:18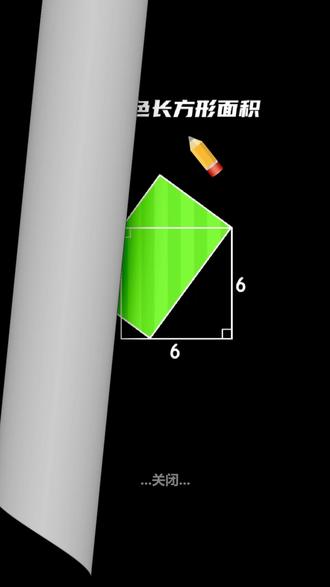 00:45查看AI文稿AI文稿
00:45查看AI文稿AI文稿小学几何拉分题,我们先回忆一半模型,以矩形的长或宽为笔,画一个三角形顶点连接平行的另一条边,三角面积为长方形的一半,顶点沿平行边随意移动,横成立, 画一条直线连接两个角,这里形成新的三角形。这个三角形和正方形形成一半模型面积是正方形的一半。 三角形和这个长方形同样是一半模型,同底面积也是长方形的一半,所以长方形面积等于正方形面积,正方形面积六乘以六等于三十六,长方形面积也就是三十六。是不是很简单?
81让数学动起来 02:11查看AI文稿AI文稿
02:11查看AI文稿AI文稿好,我们来看一道常见的几何题啊,他说 a、 b、 c、 d 呢?为梯形求阴影部分的面积,我们是要去求一个 a、 o、 d 的 面积。好, 这里面我们是不是不能够通过三角形的基本定义来求这个面积啊?好,在求这个面积之前,我们是不是可以把 o、 d、 c 的 面积给求出来?为什么?因为 a、 b、 c、 d 为梯形, a、 d 和 b、 c 是 平行的。好,那就意味着 a、 d、 b 和 a、 d、 c 是 相等,为什么 a、 b、 d 等于 s、 a、 d、 c, 因为它们共高,那么共高同时也共低,意味着这两个三角形是相等的。好,那么这两个相等的三角形减去一个共同的阴影部分,它是不是 相等的呀?那就意味着 a、 o、 b 和 o、 d、 c 是 相等的,那么 o、 d、 c 就是 六平方厘米。好,我们再看一看, 那么 a、 o、 b 和 o、 c、 b 它们是不是共底边 a、 c 的 呀?同时也共了一个顶点 b, 共顶点 b 意味着什么啊?它们的高是相等的,那么它们的高相等的话,那么意味着说 它们的面积之比,也就是底边的长度之比。那么 a、 o 比上 o、 c 是 不就是六比十 i, 也就是一比上二。既然一比二,那么 a、 c 是 不是也是 a、 o、 d 和 o、 c、 d 的 底边呢?它们同时也共了一个底,共了一个顶点 d 的 呀?意味着它们的高是不是也是相等的呀?意味着说 a、 o、 d 和 o、 d、 c 的 面积之比也是一比二,那这个时候 o、 d、 c 为六平方厘米,那么 a、 o、 d 那 是不是就是三平方厘米啊?
33飞哥小学数学 02:11查看AI文稿AI文稿
02:11查看AI文稿AI文稿a、 b 等于 bc 等于 c、 d 求角 d 等于多少度?图形又是个不规则四边形,已知条件也是三条等长的边和一个一百五十度的角。这个设定是不是有点熟悉? 直接算我们就不考虑了,直接考虑辅助先怎么做。一般的思路是连接 a、 c 或者 b、 d, 我 们先连接 ac, 连接之后 ab 等于 bc, 那 三角形 a、 b、 c 就是 等腰直角三角形, 那角 b、 a、 c 和角 b、 c、 a 都是四十五度角 a、 c、 d 就是 一百零五度,可是角 b、 a、 d 也算不出来,那角 d 就 没法算。这个思路不行, 那我们再连接 b、 d 连接之后 b、 c 等于 c、 d。 三角形 b、 c、 d 是 等腰三角形,那角 c、 b、 d 和角 c、 d、 d 就是 一百八十度,减去一百五十度,再除以二等于十五度角 d、 d、 a 就是 七十五度,可是角 a 不知道,角 d 就 还是算不出来,所以这两个思路都行不通。 这个时候大家注意三角形的特殊角有哪些呢?三十度、四十五度,六十度、九十度,这些大家都能随口说出来,其实一百五十度也是特殊角,因为它可以分成九十度和六十度。 怎么用呢?这道题我们就过点 c 做 b、 c 的 垂线 c、 e, 并且使 c、 e 等于 ab, 这样是不是就把一百五十度分成了一个九十度角和一个六十度角? 而且现在 c、 e 等于 a、 b 也等于 b、 c, 并且 a、 b 和 c、 e 都垂直于 b、 c, 那 连接 a、 e 所形成的四边形 a、 b、 c、 e 就是 正方形,这个有什么用呢? 我们一会再说。先看另一边这个六十度的角角 e、 c、 d 是 六十度,而且已知 c、 d 等于 a、 b, 现在 c、 e 也等于 a、 b, 那 c、 d 和 c、 e 也相等六十度角加两条相等的边是什么呢? 当然是等边三角形,所以我们连接 d、 e 三角形, c、 d、 e 就是 等边三角形,那三个角是都是六十度,而且三条边都相等,这时候我们发现 a、 e 也是正方形的一条边长, 和 c、 e 也相等,那 a、 e 也等于 d、 e 三角形, a、 e、 d 就是 等腰三角形,这个等腰三角形顶角是六十度加九十度等于一百五十度,那两个底角就是十五度,那角 d 就是 六十度,减去十五度等于四十五度。搞定。
3859数学?别怕! 05:32查看AI文稿AI文稿
05:32查看AI文稿AI文稿大家好,我又来讲题了,已知正方形 a、 b、 c、 d 就是 大正方形, e 是 c、 d 的 中点, e 就是 这个点。另一部分的面积是二十,就是这个一个不规则图形, 要求这个大正方形的面积。阴影部分呢,我们刚好被分成了三个三角形,给这三个三角形来编一下序号,这个是一,这个是二,这个是三, 因为同底等高的三角形面积相等,我们看 s 一 加 s 三都是用的这个底 ec, 这里的底高呢,是正方这个大正方形的边长, 然后我们再看 s 二加 s 三,他们也是用的 ec, 这条底高也是正方形的边长,所以我们我们知 得出 s 一 加三等于 s 二加三,我们发现这里都有一个三,三就可以抵消掉,所以就是 s 一 就等于 s 二,然后这里刚好有一个 两,这两条线交汇的一个点,我们就把它标成 o, 那 这个点 o, 我 们从点 o 这里做一条垂线, 那么这里接触到这里就是一个直角,那么这里就叫 h 一, 那这里也做一条也是直角,就是 h 二。 我们知道 h 一 和 h 二是长度是相等的,我们标这个点什么作用呢?看到这个 垂足我们会想到高,这里我们有三角形的高, h 二就是这个三的高 h 一, 我们把这个 二号三角形给它这个样子转过来,那转过来 bc 当做三角形二的底,然后 h 一 就变成了三角形二的高, 所以三角形二 s 二就等于 bc 乘 h 一, 因为三角形是底乘高除以二,所以这里要除以二,那么 s 三 它在底是 ec, 所以 就是 ec 乘它的高就是 h 二,然后也要除以二,我们刚才已经知道了 h 一 等于 h 二,而且这里都有一个除以二,那么 s 一 和 s 一, s 二和 s 三的差距就在 bc 和 ec 这里。 我们知道正方形它的四边相等,那么 ec 是 dc 的 一半,那么 ec 也就是 bc 的 一半,所以 s 二等于,嗯, s 三乘二, s 一 呢也是 s 三乘二, 所以阴影部分的面积就是五个 s 三,那么五个 s 三是二十,我们就可以求出一个 s 三,一个 s 三呢就是二十,除以五就等于四, 一个 s 三是四,那么我们可以把这个 s 三和 s 二看成一个整体,就变成这个样子的一个大的一个直角三角形,这里是直角, 我们再从这个点 e 这样子做一条辅助线,把这个大正方形平均分成两份, 我们先看这一半,先不看哈,先看这一半,我们发现这个多出来的空白,这个三角形刚好等于 s 二加 s 三,我们先把 s 二加 s 三的面积求出来, s 二是 s 三的三倍, s 三是自己的一倍,我们又知道了, s 三是等于四,所以就是四乘 二加一的和就等于四乘三就等于十二,所以 s 二加 s 三等于十二,那这个空白性质面积就也是十二。 这两个三角形的面积一样,那我们是不是也可以把旁边这个长方形的面积也想一下,把它这样子也分成两份,那么发现就有四分,那么 s 二加 s 三就等于这个 正方形 abc 的 四分之一。我们知道了四分之一是十二,那我们要求这个正方形就是用十二乘四, 十二乘四等于四十八,所以我们就知道了正方形 a、 b、 c、 d 的 面积就是四十八。这道题稍有点难,大家学会了吗?
21在学习的朵宝 00:35查看AI文稿AI文稿
00:35查看AI文稿AI文稿这是一道几何思维应用题,很考验娃的思维活跃度,不信你可以试试。一只小狗拴在等边三角形的墙角,墙边长三米,绳长四米,请问小狗最大的活动范围是多少平方米?以绳长为半径,逆时针绕半圈后,遇墙 墙会挡住绳子,只能活动小范围,回到原点,顺时针活动于墙后,也只能活动小范围。如图,可得到等式求出结果,你学会了吗?评论区给出你的答案,记得关注我,让学习轻松好玩!
 00:10
00:10 02:08查看AI文稿AI文稿
02:08查看AI文稿AI文稿今天给大家分享一道六年级上册的思维题,求阴影部分的面积, 如图,长方形周长是二十四厘米,图色部分面积是多少平方厘米?来看这个长方形跟圆有什么关系呢? 长方形的这条长相当于圆的什么呢?圆的直径我们用二 r 表示, 长方形的宽呢?相当于圆的半径,我用 r 表示。根据长方形的长等于二十四厘米,我们可以列出这样一个方程, 长加宽的和乘二,这是它周长。周长等于二十四,三二乘二等于六,二等于二十四,求出二等于四,我们求出它的半径呢? 为四。那我们求阴影部分的面积怎么求呢?阴影部分的面积我们可以用长方形的面积减掉半圆的面积。 那长方形的面积怎么求呢?我们知道它的半径是四,宽是四,长呢?长是两个半径,四乘二,这是长, 再乘宽四,算出长方形的面积。接着再求半圆的面积,我们知道它圆的半径是四三点一四乘四的平方,它是个半圆,得再除以二 等于三十二,减二十五点一二求出来,等于六点八八 平方厘米,所以阴影部分的面积是六点八八平方厘米。同学们,这道题你学会了吗?
17思思老师






