setw函数的头文件
我是老妖,今天咱们来聊聊 c 加加内置函数中 set with 函数。在 c 加加中, set with 函数就好比一个负责管理输出内容的管家,当你需要输出一些内容时,他会按你的心意定好输出内容的宽度, 使得输出的内容看起来更整齐、更美观。 sat wage 的语法是这样的,括号里的预宽是你希望设置的自断宽度,这里的预宽一般放整数, 不过你偏要放小数也没关系。 set with 函数最后都会取整数的,比如 set with 括号八点三,最后设置宽度时一定会取整数八。 接下来让我们用一组代码来实践看看,这是一个可以输出自定义几行几列正方形的代码。先看这个头,文件里包含了 set with 函数。 接下来我们在主函数中先定一个整形变量 square size, 用于存储你输入的数字。假如你输入六,就代表你希望正方形的大小是六行六列。 然后我们用嵌套的否循环,也就是一个循环,内部还有另一个循环。这里先是我们的外层循环 i 从零开始,每次增加一,都会执行一次内循环,内层循环的,这也是从零开始,每次增加一,一直循环到你输入的正方形大小的数据 才跳出循环。当执行完一次这个内循环后,就轮到我们的 c alt 语句出场了。这里的 set with 三是为了设置下一个输出字段的宽度为三,后面的字符信号就是我们要输出的内容。在这里我们就要理解为 set with 函数后紧跟的内容的 宽度为三。在这句代码中就是指星号占一个字符宽度,星号后面还要加两个字符宽度的空格。这句的意思是每跳出内循环一次,就要执行换行, 然后我们综合的来看看这个嵌套否循环。首先我们有一个外层循环,用来控制组成方块信号的函数, 这里的 i 每循环一次就加一,直到 square size 等于我们输入的方块大小数字。假如我们定 square size 为六,那么外层的 for 循环中按满足小于六的条件, i 字增益之后进入 four 的内循环,就刚开始的值为零, 小于六符合条件。这一次争议之后,执行 see out, 输出一个信号两个空格。 see out 语句执行完成后,返回否循环,继续判断这是 时 j 等于一,依然满足小于六的条件, j 继续自增一执行 see out, 依次类推,直到 j 等于六,跳出内循环,执行这个换行语句, 然后返回最外层的 for 循环,判断 i 等于一,是否满足条件。由于 i 等于一,小于六,自增以后继续执行这个 for 的内循环。就这样的思路,我们最后会得到由信号组成的六行六列的正方形图形。下面我们编译运行一下 输入六,也就是给 square size 复制六,我们就得到了这样一个六行六列的星号组成的正方形,且由于我们的 set with 三的加持,每个星号和下一个星号之间这个宽度为三,如果想要调整宽度,改变 set with 括号里的 参数即可。聊到这里,应该对 saturate 函数有个了解了吧,有问题请在评论区艾特老妖,听说给老妖点赞的人三日内必有好事发生。
粉丝77获赞313
相关视频
 26:01查看AI文稿AI文稿
26:01查看AI文稿AI文稿一口气讲完欧米伽的取之范围,这个题型是每年高考必考题,这期我们用四个题型彻底帮你知根知底。 我们来看到第一个题型哈,固定起点,你是说你起点带进去,它是固定的,已知 f x 等于这么多它的图像,关于这个点对称,好,这是第一个条件,且 f x 在 这一段上单调,这是第二个条件。我们先分别来解一下这两个条件哈。 首先第一个条件嘞,怎么解呢?就是说我这一坨东西啊,在这它是一个对称点,也就是我们不妨去令 t, 它是等于 w x 减三分之派的,然后嘞,这时候把这个六分之派带进去,六分之派 omega 减三分之派。此时来,这个 sign t 的 图像,我们可以画一下哈,它是这个样子的,那么它的对称点到底在哪里取得?是不是零加上 k 派呀?对吧?所以呢,这它就代表的是咱们 sign t 的 对称点,也就是零加 k 派的。 ok, 六分之派,欧米伽等于三分之派加 k 派,左右两边同时把这个六分之派给它消掉哈,就等于多少呢?等于二加上六 k 的 好,我们就得到了第一个条件,就是欧米伽等于二加六 k 的, 然后你再结合说,我的 omega 是 大于零的,此时呢,你就可以得到说,哎,当咱们的 k 等于零时,此时 omega 取的是二,当 k 等于一时,此时 omega 取的是八,就这样写下去哈,这是第一个条件。我们再去看第二个条件,它说 f x 在 这一段上单调, 也就是说什么呢?咱们的 t 呀, t, 它是等于 omega x 减三分之二的,我们去给它整体换元, 换成什么来?就是零带进去,也就是负三分之派,然后来四十八分之五派的进去,也就是四十八分之五派 omega 减三分之派的。好,我们的 y 等于 sign t 啊,它其实在这一段上是单调的,那你就会发现咱们 sign t 的 图像是非常好画出来的。 ok, 我 们来看一下哈,此时来我们的负三分之派在哪里啊?是不是在这取得呀?对吧?这里是个空点,不能取到。然后呢,我往右边走,哎,他说我在这一段上都要单调,那其实就是单调立增嘛, 但是如果超过这一条对称轴,往后边走来,他就是单调立减了,所以我们的右端点他一定是不能超过这一条对称轴的,也就是二分之派的。 所以这种题型就叫做,哎,我的起点固定了,那么我只用去看终点在哪就可以了。而这个起点固定是由谁决定的嘞?就是由这里的零决定的哈,所以你看到零开头的题目,你就知道这是固定起点题。那么此时我的四十八 分之五倍 pi omega 减三分之 pi, 他 就应该干什么呢?他就应该是小于二分之 pi 的, 那这时候他能不能取?等来你就去假设他取,等了取,等了之后,在这他仍然是一个空点呐,对吧?所以说我在这个空点到这个空点上,他仍然是单调递增的,所以呢,他是可以取得的。 此时哈,我左边还要带一下哈,我是大于什么呢?大于咱们的负三分之派的, ok, 它就是大于左端点嘛,但其实它一定是大于左端点,因为咱们的 omega 大 于零,而这一坨东西就大于零,它再减一个负三分之派,那肯定就是大于左端点的哈, 所以呢,由这个条件你去解出来,咱们的 omega 它是小于等于八的,大于零的哈,这个大于零在题目中已经暗示了,那么此时来 omega 小 于等于八,而我们刚才算出来, omega 是 在二加六 k 上走的, 所以呢,我们就只能取二八,八加六等于十四,这些都取不了了,只能取这两个数,所以呢,最后答案是选 c 选项,同学们不要着急记笔记,这几个的讲义和课后预习我全都整理好了,一定要下课后多复盘几次,点击我的主页置顶群聊就可以领取。 我们先来看一下哈,如果他题目问的是说我的 f x 在 a 到 b 上有多少个零点型的题目,他是非常常考的,他其实是有结论的,我给大家推导一遍哈。 首先,如果 f x 在 a 到 b 上有一个零点,那么此时来咱们把 f x 的 图像给画出来了,他是按照 t 就是 多少个周期来区分的, 那么咱们 b 减 a 这个区间长度嘞,它是可以怎么看的?我们先去看,如果说我们从第一个零点出发哈,我们要走多久才会遇到另一个零点嘞?我们其实只要从这个零点 得左边一点点出发,那么我们就会很快的遇到这个零点了,对不对?所以说我左边大于这个数呢,它是非常非常小的,其实只要大于一丢丢,把这个零点给它包括进去就可以了,对吧?所以说它一定是大于零的,那么此时它是小于什么的嘞?就是我从这开始走, 我从这开始走,就是看他最长能拉伸到哪里,对吧?然后你看,哎,通过来,通过来,然后你就会发现,哎,刚好在这有一个零点了,但是左两边这个零点我都是取不到的,因为他是一个开区间吗? 此时呢,他就是刚好有一个零点的,这就是他能撑到的最大的区间长度。但如果说我继续往这边走,我的终点继续往这边走哈,那么他就把这个零点也取进去了,他就有两个零点就不对了,所以此时哈,他最长就是在 t 这里的,这里呢,是可以取懂的, 因为取懂了,反正两个人都是一个开区间吗?对吧?都是开区间,所以刚好就把中间这个零点给他取到了。 我们再来看,如果说 f x 它在 a 到 b 上有两个零点,那么此时嘞,我们从这开始走哈,从这里开始走,一个两个,哎,从这里开始我就会得到两个零点, 但因为呢,它是开区间哎,我在这哈,我是取不到这两个零点的,所以我必须要稍微的往左右两边延伸一丢丢,非常一点丢丢,它就可以取到这两个零点了哈, 所以左边来,他应该是二分之 t, 但是我取不到等,因为我一定要比二分之 t 稍微大一丢丢,才可以把这两个零点给他包括进去,然后这是 b 减 a 的 长度,然后他是小于多少嘞?我们再来看,从这开始走哈,他是一个空点开始走, 空点开始走,走走,走好两个零点了,两个零点了,这是两个零点。好,我们再撑到这,最多撑到这就不行了, 再往左两边走的话,他就开始可以把这个零点和这个零点也给他包裹进去了哈,所以你看此时的话嘞,他的区间长度一共是多少? 是不是一共是二分之三 t 啊?对吧?所以他是小于等于二分之三 t 的, 他是可以驱动的。那么我们再来看,如果他有三个零点嘞,三个零点,那其实也是一样的,从第一个点开始,一个两个 ok, 那 么他的区间最短的是不是再往左边走一点,再往右边走一点, 那么此时它的区间长度就是 t 的, 那么我们的 b 减 a 的 绝对值长度一定是要大于 t 的, 取不到,等了哈,然后我右边是一个什么嘞,就是我从这开始走走走走走,这里一个、 两个、三个,三个零点可以取到了,但是我最终的这个终点是不是一定是在这一段上啊?对吧?就是我这个终点最长最长走到这了,因为我再往这边走,再往这边走,它又是可以取到更多零点了,所以此时呢,它的区间长度最多就是二 t 的, 它是可以取到等的哈。 那么大家去观察规律之后就会发现,哎,我好像左边的东西,我左边这个端点,我都可以写成什么二分之 n 减一倍 t, 而我右边都可以写成是二分之 n 加一倍 t 的, 你们看,当我有一个零点时,我左边是不是二分之 n 减一倍 t 啊?对吧?所以 n 等于一带进去,就是二分之二,就是等于 t 的, 而这里呢,就是二分之多少二减一就是二分之一倍 t 的, 而这边是二分之二加一至二分之三倍 t 的, 而在这种情况下,就是二分之 n 减一倍 t, 就是 三减一,就是二分之二嘛,对吧?然后呢,右边就是二分之三加一至二分之四也至二 t 的, 所以左右两边都对上了,然后呢,这里是左边不能取等,右边可以取等的。然后呢,这种情况是为什么呢?是因为题目给的条件它是一个开区间, ok, 所以 我们就记住了说,哎,如果是开区间的话,我们就是在右边取等的。好吧, 那么其实我为什么要发明开区间右边这一个口诀嘞?因为我为了补上另外一个口诀,就是 b 左, 如果是一个 b 区间的话,那么我们就是在左边取到等等。我们来看这样的三种情况, 如果说 f x 它在 a 到 b 上有一个零点,那么此时来哈,你看,我们两个都是 b 区间,都是可以取到这个点的, 那么我直接从零点开始走,在零点结束,可不可以啊?可以的,所以咱们 b 减 a 的 长度,它可以最小是零,那么此时是不是刚好有一个零点了,对不对? 所以呢,这是左边可以举到动,然后我们继续来看哈,如果我们端点从这开始,哎,走走走走走,你会发现我不仅中间是有一个零点,我左右两边还有两个零点的,那么此时哈,我真正的这个端点呢,他肯定是要往这里面收一点,这里面收一点的, 所以呢,我 b 减 a 的 长度,它绝对是不可能大于 t 的, 如果说我等于 t 了,我等于 t 了之后,它就会出现三个零点,对吧?所以呢,它只可能说我再稍微往上面一丢丢,这样走,我 尽量把它称的很大哈,最多称大到 t 这个程度,但是呢,我不能取等哈,所以此时呢,右边就是不能取等的。我们再来看第二种情况,他在 a 到 b 上有两个零点,哎,有两个零点,他最小是多少来?是不是就是从这走到这就是二分之 t 嘛,对吧?他也是可以取等的, 但是我要去说明一下,就是我有了两个零点哈,我确定了,就是这两个零点, 我们向左右两边延伸,哎,延伸延伸,延伸到这就不行了,我就取不到这个点了,我只能在他稍微往上一丢丢,否则我又多了一个零点,对吧?我这边也是,我再往这边走不行了,我再走到这的时候,我又是马上又会产生一个新零点, 所以咱们右边他是不能取到等的,而是二分之三 t 就 刚好小于他哈。那么如果是三个零点情况下,他最短就是取这三个零点嘛,加在一块就是 t 嘛,他肯定是可以取到 t 的。 而此时嘞,如果是三个零点,我们确定了是这三个零点,好,我们再向左两边分别延伸这么多,分别延伸二分之 t, 但是在这肯定是不能取等的,所以咱们的 b 减 a 嘞,它肯定是要干什么?它是要小于二 t 的。 所以你会发现,其实跟前面这一页我们做的东西上面,我们的左右端点是完全一致的, 都是二分之 n 减一倍 t 和二分之 n 加一倍 t 之间的。但是呢,我们的取等条件是不同的, b 左开右,这里是 b 区间,那我就是左边才能取到等的哈, 所以大家就已经理解了这一个由多少个零点去推他的 omega 的 粗略范围。其实这些题型我都整理在我的逆行北大解析一百招里了,如果你拿到这份资料,你会发现数学真的只是执行程序。点击我的主页置顶群聊就可以领取。 我们来看到第二个类型题哈,就是不固定起点的题目,它就开始变难了,这时候呢,有一个零点,已知 f x 的 图像是由这一个函数,它告诉你解析式了, omega 大 于零的图像向右平移三分之派个单位折到的。 若 f x 在 这一段上仅有一个零点,那大家思考一下哈,如果说咱们最初的图像,它是不是这个样子里,对吧?它是这个样子的, 然后嘞,我向右边平移三分之派个单位, a 得到了这个样子的,然后此时嘞,我的这个函数图像,我在二分之派到派上仅有一个零点, 那么我如果说哈,我去对这一个做平移,我写成是 omega x 左加右减就是减三分之派,再加三分之派,它就会变成什么呀? 同学们,它是不是就会变得很复杂?它里边打开就是 omega x 减三分之派, omega 再加三分之派,所以你看到前面后边都是会出现 omega 的, 它就会变得很复杂。那你应该怎么做嘞?我给它平移回去啊,对不对? 我现在给它平移过来,是在二分之派到派上,我的图像其实是没有变的,那我给它平移回去,我就向左边平移三分之派个单位啊,我就又得到了这个函数图像,对不对? 那么此时咱们的区间二分之派到派上,他向左边平移三分之派个单位,是不是就得到了二分之派减三分之派,然后嘞,这里是派减三分之派就给他平移回来了呀,也就是六分之派到咱们的三分之二派之间的。 那么这道题呢,他真正想说的是,哎,咱们前面这一个函数,我这一个二派之间的。那么这道题呢,他真正想说的是,哎,咱们前面这一个派到三分之二派上只有一个零点, 这时候呢,这道题才会变得稍微简单一丢丢, ok, 他 只有一个零点之后,那么我们就是两步走法则,第一步是干什么呢?就是我们要去确定好我们欧米伽的大致范围, 然后呢,刚刚给大家讲了公式的推导哈,咱们的区间长度,也就是此时的三分之二派减六分之派,它是不是应该大于二分之 n 减一倍 t, 小 于二分之 n 加一倍 t, 然后在哪里驱动嘞?就是由咱们的口诀哈,就是 b 左开右,哎,咱们此时哈是一个 b 区间, b 区间,所以说我们应该是在左边驱动的。好,我们再把这个一给他带进来哈,左边带一就是零的小于等于,然后中间可以给他解出来哈,也 就是六分之四派减六分之派,也就是六分之三派,也是二分之派的。然后呢,他是小于右边的多少嘞,这个一带进来就是二分之二 t, 也就是 t 的 哈, 此时嘞,我们这里肯定是可以取到的,我们看一下右边二分之派小于二派除上 omega 的 绝对值, 而 omega 是 大于零的,所以可以直接去掉绝对值符号解得咱们的 omega 它是小于四的,然后呢,它又是大于零的,我们就得到了 omega 的 初步范围。 那么我们第二步是干什么嘞?我们要试图去确定起点,然后呢,把起点用来分类讨论。 好,我们此时呢哈,把这一坨用起点带进去,起点就是六分之派嘛,对吧?所以起点呢,它就应该等于六分之派, omega 加上三分之派的。只要我们能确定起点在哪一个区间,那么我们就可以对起点的位置进行一个分类讨论。 此时嘞,我们把 omega 的 范围带进去,零到四等,所以它算出来哈,就是零加三分之派,也就是三分之派等,而这个四带进去嘞,就是六分之四派,也就是咱们的三分之二派,再加一个三分之派,哎,也就是派,所以咱们的起点它是在三分之派到派之间的, 而我们这个函数图像是 y 等于根号二倍 sine t d 的 吧,所以呢,我们把它的函数图像给它画出来,哎,也就是这个样子画出来了。然后我们的起点是在哪取得?是不是在咱们这一段和这一段上取得的? 所以你会发现呐,我在这一整段上取它都是没有穿过零点的,它都是不存在零点的。那么咱们的中点是在哪里嘞?是不是带右端点的三分之二派,也就是三分之二派。然后呢,欧米伽加上三分之派的, 你们可以看一下,我的起点在这哈,然后我穿过去往下面走,这里就出现了一个零点,好,继续往后面走,在这就不行了,我不能在这有零点,只能在这出现一个零点,所以我们的终点应该是在这一段之间的,对吧? 所以呢,我们把终点给他拿下来,他就应该是大于咱们的,这里是派,这里是二派,他肯定是在派到二派之间的,但是具体哪里可以去等嘞?你就去假设他可以去等, 如果说我前面假是可以取动的哈,而我们的起点是在这一段之间的,我们的起点从这开始,然后呢,走到这一段上,哎,你看,他确实在这停住了,他是在这一段上,他是出现了这一个零点的,有一个零点,对不对?所以呢,前面是可以取动的。 好,我们继续来看,假设说我右边是可以驱动的,所以说我们的起点不妨落在这哈,然后呢,我们的终点是在哪?是在这,所以我们就这样走过来,你会发现不行,这里出现了一个两个两个零点的就不行了,所以这是不可以驱动的, 我们就由这一条哈,假设它可以驱动,就推得最终真正的驱动条件。好,我们自己去解一下哈。 omega 就是 在一到二分之五的左臂右开区间的。 最后嘞,你是要综合这两个条件来得到最后的条件就是咱们的一到二分之五的左比右开,是不是选咱们的 c 选项? 我们来看到这道题哈,它是不固定起点的两个零点型的题目。若函数 f x 为这么多,它是扩散开头的,在区间上恰有两个零点,那么 step one 就是 由这个有多少个零点去粗略估计咱们的欧米伽的曲值范围,对吧? 此时来我们的区间长度也就是二分之三派减二分之派等,它是应该要大于咱们的多少呢?二分之 n 减一倍 t, n 呢,是为二的,所以是二分之一倍 t n, 它是小于多少了?二分之 n 加一倍 t, n 加一直是二分之三倍 t 的 这么多,然后在左边还是右边取等来,就由咱们的口诀哈,就是 b 左开右,哎,这是一个开区间,那么就是在右边取到等的, 此时嘞,咱们的 t, 它是等于二派除上 omega 的 绝对值的,而 omega 大 于零,所以呢,就是二派除上 omega, 这里直接打开绝对值符号哈,我们代入上面这个式子去解一下, 你们就可以解出来我们的 omega 的 大致范围嘞,它首先应该是在一到三的左开右闭区间之内的。好,这是我们的第一个粗略范围, 那么得到了这个粗略范围之后,第二步是干什么呢?就是由这个范围去反推咱们起点到底在哪个区间,并根据这个区间进行一个分类讨论。好,此生的话,我们可以去把起点给它写出来。是不是把二分之派给它带进去就是起点了呀? 也就是咱们的二分之派欧米伽加上五分之派,又因为咱们的欧米伽是在这样一个范围中取得的,所以呢,你给它算出来哈,它是应该在十分之七派到十分之十七派的左开右闭区间上的。 所以呢,我们再去把这幅图给它画出来,这是咱们的 cosine t 这个 t 哈, cosine t 的 图像给它画出来。 好,我们来观察一下,我们的起点呢,是在十分之七百到十分之十七百之间的,十分之七百在哪呢?就是在这边,对吧?就是在这开始的, 这里的对称轴是派的,这里的对称轴是二派的,此时嘞,他就是在这开始,然后往这边走,走到咱们的十分之十七百,他肯定是小于二派的,对吧?他这是在这,所以他应该是在这一段上开始走的, 那么此时你会发现它穿过了 x 轴,所以说它在零点的左边,还是说零点的右边就很关键,这里就是咱们的分类讨论依据,如果说它在左边的话,那肯定我等一会算零点,是不是从它开始?如果说我在右边的话,那我算零点,是不是肯定从这里开始? 所以我们的分类讨论条件就得到了,此时咱们的起点二分之派 omega 加上五分之派,它是在第一段上,也就是十分之七派到咱们的二分之三派之间的哈,也就是在这一段上, 那么咱们的第二种分类讨论条件哈,就是二分之派 omega 加上五分之派,然后嘞,他应该是在第二段上,他就是大于等于二分之三派,再到最后一段也是十分之十七派之间的哈,所以一共是两种分类讨论条件。我们先去看第一种, 第一种的话嘞,我们的起点都是在这些地方取得的,都是在这些地方取得的,所以说我从这开始走,我要经过两个零点,好,这两个零点一定是要经过的, 那么第三个零点我就肯定不能经过了,所以说我们的终点应该是在这一段之间的,卡死了。先是咱们的二分之五派到二分之七派, 但是此时哈,我们的终点到底是这里可以取等嘞?还是说这里可以取等了?你要去观察一下,如果说我们的终点哈在这可以取等了,又因为咱们的终点他是取不到等的,一个开区间,对吧? 对呢,我们就是从这开始走,开始走,开始走,开始走,好,走到这的时候, ok, 我 们在这取懂了,你就会发现他只经过了一个零点就不行了,这里就是不能取,懂了,再看这里能不能取懂。好,我们从这里开区间,开区间,走走走,走走, 走到这的时候,哎, ok, 这里也是开区间,所以呢,此时这里这里两个零点刚好的就可以了哈,所以呢,我们再来写一下终点, 终点呢,左边是二分之五派,右边呢是咱们的二分之七派,而左边是不能取等的,右边是可以取等的。终点是哪一个嘞?这是咱们的二分之三派代入这个式子里面来也是二分之三派 omega 加上五分之派的。好,这两个东西我们一起去解出来咱们 omega 的 范围哈。 第一条就是在十五分之二十三小于 omega 小 于等于五分之十一的这第一个情况, 我们再去看第二个情况,咱们的起点从哪里开始了?是从这开始了,而咱们的起点呢,他是一个什么?他是一个开区间,所以呢,他也是这个样子的, 他也是这样,然后我就往右边走走走,走了两个零点之后,哎, ok, 两个零点过了,那么咱们的终点他也是一个空点,对吧?所以呢,我这个空点是不是仍然是在这一段之间取的?二分之七派到二分之九派之间, 那么此时来我左边能不能取档?不能,因为如果他取档,他就是一个空点,在这只有一个零点的,那么我右边这里能不能取档嘞?那肯定就可以了,对不对?因为我在这走过来两个空点,这里还是有两个零点的, 所以此时咱们的中点是在二分之七派到二分之九派之间,而一个是空点,左边是空点,右边是一个可以取档的点。然后呢,咱们的中点是这个样子的 好,此时呢,我们去推出来哈, omega 的 取值范围,它就是在五分之十三到十五分之四十三之间,然后两边儿都是 b 区间的。 然后最后呢,你要去检验这两条它是不是符合一到三之间的,哎,你会发现都刚好符合。那么最后的答案就是,这两个并在一块的是不是选谁啊?是不是选咱们的 c 选项啊?其实当大家哈算出来第一种情况的时候,你就会直接选 c 选项了, 因为这道题它肯定是两个区间并在一块,所以只能选 c d。 而 c 和 d 它的区别不仅在这一坨,它这一坨哈也是有区别的,都是有区别的,所以你只要选出来正确的前面这一坨,后面这一坨,你其实都不用算了,选填题里面做起来会更快哈。 那么同学们,如果这道题哈,我再给大家改一个问的方式,你们看会不会做?他说若阔撒眼,在这个区间上,他是单调递增的,应该咋整啊?同学们, 我说它是单调递增的,应该怎么办?那仍然是两步走,因为第一步应该是干什么?由它给的条件得到 omega 的 大致取值范围,所以此时呢,我们的区间长度也就是二分之三派减二分之派的,它应该是干什么?它应该是 应该是干什么呢?小于一个单调区间长度的,咱们的单调区间长度是不是为二分之 t 呀?对吧?所以它就应该是小于二分之 t 的, 它可以取等哈,因为取等了之后嘞,哎,它还是一个单调区间之内的。 那么此时嘞,我们去解一下,左边就是 pi, 右边嘞就是二分之一乘上二 pi 除上 omega 的 绝对值,又因为 omega 大 于零,所以呢,解到 omega, 它应该是小于等于一的。好,这就是咱们解到的第一条性质, 那么第二条是什么呢?根据这个 omega 的 粗略取值范围,我们要去干什么?我们要去带入起点来观察一下我们的起点是什么嘞?是不是二分之 pi, 欧米伽加上五分之派,它应该是属于多少啊?零先带进去,也就是五分之派。到咱们的一带进去,二分之派加上五分之派,也就是十分之七派的。那么此时我们来画图看一下哈,我们的 cosine t 的 图像是这个样子的。 而此时来我们的起点是在哪里啊?这里是派,这里是二分之派,起点是在五分之派到十分之七派之间。哎,他是在这到这之间,说明咱们刚才提出错了哈,不应该是单调递增, 应该是单调递减,所以你看,我们的起点在这里之间,那么我们的终点来 我们的中点是不是也必须在这一段上单调递减啊?对吧?所以中点你可以去算出来,也就是二分之三派,欧米伽加上五分之派的,它应该是干什么小于等于派的呀?它应该小于等于派, 所以呢,你再由这一条式子去得到欧米伽更精细化的范围,然后你就能得到最终的答案了。 视频的最后,我给大家准备了三份非常重磅的干货,分别是四十页的逆袭北大解题一百招,还有两万字梳理我为什么从五十分进不到一百四十六分的数学底层学习方法?最后来是为前五十名同学赠送一个免费的数学成绩分析和规划, 点击我的主页这个群聊,就可以免费领取。数学想要考年级第一,从来不是天赋,而是执行程序。我是北大堂,我们下期再见!
1225北大糖的魔法数学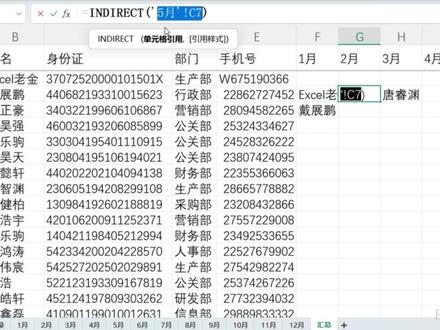 06:25查看AI文稿AI文稿
06:25查看AI文稿AI文稿前面视频呢,我们讲了用 indirect 呢来引用各自的表统计数据, 那么相对这个函数呢,是比较不常见的,我们今天呢来稍微讲一下这函数,大家看的同时呢也帮忙点点赞,有不懂的呢也可以发在评论区。 首先我们在引用数据的时候,比如怎么引用,等于我们在选择当前汇总表,随便选择一个,比如说这里有个 号码好,我们点过后就能引用到一二单元格的数据,那一二呢就是一个单元格地址, 字母代表类,数字代表行。好,我们还有一种情况,等于一月 b 二单元格回车,这样点了过后呢,我们就能引用一月份 b 二单元格的数值,会引用到这里来, 这里呢第二个属性我们已经知道了,那在他前面的会有一个感叹号,感叹号的前面呢,那就是他对应的工作表名称,我们引用单元格本表的, 他是没有工作表名称的,那其他表也就是我们指定哪个工作表,那就需要在前面引用名称 回车,那这个呢就属于是一个引用的地址的问题,当然我们还有可能会引用一个其他工作部,我这里新建了一个工作部,我们可以等于 这个工作部的这个地址回车,那他呢有个中括号,工作部名称表名称 单元格,这是整个单元格常规引用的一种方式,我们以这个一月份这个表的单元格去分析,这里呢是引用,我们可以改成三, 但是呢我们在这里输入一月回车,那他就不能够识别这些内容。再来,比如说我们再输入 b 二, 外面加了两个双引号呢,也就是说把这个 b 二变成了一个文本回车,他呢就变成了一个文本,就不是单元格了。我已经告诉表格他不是单元格,就是 b 二这两个字, 这就是引用与文本的差异。那我们 indirect 呢,它呢就是把文本变成单元格引用,我们比如说我们输入双引号, b 二, 双引号回车,他呢就引用到了这个 b 二单元格,那文本我在下拉的时候呢,那也肯定就不会动。讲到这里呢,我们应该稍微的就了解了,哦,原来 indiewact 是 把一个文本型的制服串 转换成单元格引用,那么我们这里相对来说引用的是一月份表的 b 三,我们在它的两边加上双引号呢,它是不是就是一个文本就不能返回任何数字?我们把它给复制 给 indirect 回车呢,它就能得到一月份 b 三,单元格呢,它就是带整棚, 这个的作用呢就给我们对于单元格地址呢做了一个可操作空间,比如说我们把它的三连上肉 a 三板块号 回车,那我再往下拉,那我就能获取到整个一月份表对应的数据,看下一月份表, 熊正豪、彭浩强是吧?熊正豪和彭浩强他就能获取到了。那我们最常用的就是这种前面期呢有讲到的跨表引用的问题,比如说 好,我们现在要把表一月这个字变成二到十二,相对来说这个一字呢就要去发生变化吗?好,我们把变化变在哪里?把一字去掉,双引号打上,这个呢是工作表的一些特性 啊,不带符号的部分呢,不要这个单引号也是可以的,我们直接 call 了 a 一 连上,那 column a 一 呢?就返回 a 一 的类号, a 一 是第几类呢?第一类我们就是一月,如果我往右边拉一类呢,拉到 b 一 的时候呢,它就是二月。好,我们回车看一下带针蓬,比如说拉上去一格, 哦,这里拉上来呢,这个 a 一 就没有了,我们换回 a 一 回,撤下脑筋,好再拉过去一个人,再拉过去看一下, c 一 就是三,那应该来说就是三月的 b 二单元格是多少?三月的 b 二单元格 唐瑞元,是吧?这样呢,我们就能通过一个文本,我们选中这个参数,按 f 九呢就能得到它计算的结果。三月这个是表名称,那 b 二是单元格地址。好,这串文本转换成单元格 尾车呢,就得到了唐瑞渊,这个呢就是这个函数的基础。至于我们最终要怎么使用呢?就在这串文本里面怎么去构造一个它,最终引用单元格的地址。常规的来说,我们是可以去先 点他点一个看看,对吧?这样呢,我们就能得到这串制服,我们想办法去变动这些制服的结果,学会了记得点赞哦。
48Excel老金 13:13查看AI文稿AI文稿
13:13查看AI文稿AI文稿同学们好,今天我们来讲解操作题当中的 excel 表格,那首先咱们来看一下这一道题目, 打开文件夹中的期中考试成绩表,完成下列操作并保存。那我首先已经把这个 excel 表格打开了, 那首先第一个题,使用函数算出每个同学的八门课的总分, 使序列填充在 k 二到 k 十二单元格中。那首先 k 二是哪个?是不是这个单元格 k 十二呢?是不是它要把这些同学的一个总分算出来,那求和,你看总分对吧?那求和那要用到我们的一个什么函数,是不是叫 sum 函数,你看一下,这里有一个函数, 我们可以插入函数 sum, 他 说返回某一单元格区域内所有数值之和啊,那我们确定,你看那怎么去使用呢?那我可以怎么样? 他要求总分对吧?那我这个同学的总分是不是按住鼠标键,从 c 二一直拖,拖到哪里?是不是拖到 j 二?那这个呢?就是我们这位同学的一个总分啊,那你可以看到这个操作结束后, 这里有我们的一个函数的写法,对吧?等于 sum c 二到 g 二啊,也就是求 c 二到 g 二的总和。那这样的话呢, 我们第一位同学都算出来了,他说让序列填充在下面的单元格当中,那也就这些都要算,那我总不能一个一个的去点,对吧?那我们就要使用到填充柄,那首先点击这个单元格, 放到这个单元格的右下角,当鼠标变成实心的十字交叉这种符号的时候,我们向下拖拽,哎,一直拖拽到哪里? k 十二啊?那这样的话,我们就可以使用自动填充来把所有人的总分都给他算出来,那这个呢,就是我们的第一道题啊,求总分。下面我们来看第二道题, 他说使用 rank 函数,求每个同学的总分成绩名次填充在 l 二到 l 十二单元格中,那也就是在哪里是不是这么多, 也就把每个人的名次都算出来,对吧?那你看一下他说 rank 的 作用是怎么样返回他的大小排名啊?例如他 就表示 e 三啊,在这个区域内的排名,那也就是我们可以根据它这个来写,对吧?一模一样的,我们可以在这个函数这个框当中, 根据它这个来写等号啊, rank rank 函数,然后呢小括号,对吧?哎,最好是先把这两个括号先写上, 那么接下来呢,我们要在括号里面填我们的参数,那第一个参数呢?它是表示什么?看一下,它说表示这个单元格在 这个区域内它的一个排名,那也就是第一个参数是我们所需要排的那个数据,那也就是我们这里的这位同学总分 这个单元格是什么?是不是 k 二呀?那所以写 k 二,那在哪个区域内呢?是不是在 k 二到 k 十二这个区域内,总分是不是只有这么多,他在这个区域内进行排名,所以呢,根据这个规则来,对吧? 那也就是 k 二到 k 十二。那咱们有没有发现他前面行号和列号前面都加了一个什么美元符号,那这个呢?是我们的绝对引用啊,那他这里用了绝对引用,那我们也去用它,因为以防我们的行号进行改变了之后呢函数出错。 好,那美元符号怎么输入呢?需要在英文状态下去,先按住键盘上的 shift 键不放,然后呢去按我们字母键的上方有一行数字,去按住那个四, 那这样呢,就可以实现我们输入美元符号啊,美元符,然后呢是什么?在哪个区域内? k 行号和列号前面都需要写啊?都需要写美元符,然后再写一个美元符二,然后呢一个冒号,然后再一个美元符什么? 再一个美元符十二,那所以呢,这个就写好了,那按下回车, 也就是我们的 enter 键,那我们这个同学他的名次就排好了,那根据我们第一道题同样的原理,把我们的鼠标放到这个单元格的右下角啊,变成十字交叉实心箭头,就可以使用填充柄, 那这个呢就是第二道题。好,那第三道题呢?他说对于名次列进行声序排序,那名次列是不是 l 列?我们点击这个 l 列鼠标左键,然后呢去点击我们的一个 排序,选择什么题目当中要求声序排序啊?扩展选定区域排序,那这样的话呢,我们是不是按照名次的声序进行排序了,对吧? 好,那这个是我们的第三道题,第四道题呢,他说以考号和总分两列为数据圆,生成这个 柱形图,图表明期中考试成绩。那我们来看一下。啊,啊,生成这样的一张图,那我们首先要干嘛呢?去,他说以考号和总分这两列数据,那么考号是不是这么多, 也就是 a 一 一直到 a 十二,对吧?那这个列是考号列总分呢?是不是 k 一 到 k 十二,对吧?那我们要怎么样去同时选中这两列呢?首先鼠标点击考号这一列, 然后一直往下拖,拖拖拖,哎,你发现啊,有一个绿的框框给它框住了,那也就是目前选中了 a 一 到 a 十二,然后按住我们键盘上的 ctrl 键啊,键盘的左下角有一个 ctrl 键按住不放, 然后呢鼠标再去从这个 k 一 一直拖拖拖一,一直拖到这个 k 十二,哎,那这个就同时选中了啊,把它拖完了之后,你就 ctrl 键可以放掉了,然后呢我们就去点击插入, 我们插入什么啊?图标插入柱形图,那么点击,哎,出来了,这样一张图就出来了,那咱们看一下他和我们这个要求有什么样的区别? 这张图我们这张图有什么区别?是不是他这个标题不一样呀?那我们看一下我们第四道题,他是说什么?他说是不是要把图要标题改为期中考试成绩,那我们呢,就可以 双击这个总分这个地方,我们就可以把它修改啊,就可以打字 把它修改掉,那这样的话呢,是不是就是期中考试成绩标题了?哎,那有没有看到我们这我这生成的是不是还多了一个,那我们怎么把它去掉呢?这边呢有一个 第一个按钮,它可以什么隐藏掉我们这里的什么东西?图例,哎,你看它把它隐藏掉了,是不是就可以了?那也就是说我们这里图标的元素我们都可以去给他添加或者隐藏啊, 具体的以你的题目要求为准,尽量做的和我们的参考图一样。那由于我们这里的 wps 版本呢,可能不同,所以呢,你去插入的时候,可能那个插入图标呀,你可能选的跟我就不一样啊,但是内容大差不差。 那这个呢,就是我们这个第四道题啊,你看一下生成一个图标,对吧?好,那生成完之后呢?第五道题,他说什么保存文档并关闭 wps 啊?点击保存,这有个保存,那 随后呢就把这个文档给它关闭,那我们这道题呢就做完了好了,那这个呢是我们这个题目啊所要求的这些,那其实在我们考试当中呢, 还有一些常考的点,比如他让你呢去插入一行标题,那我们可以怎么插入?把你的鼠标放到这个行号这里, 点一下第一行,然后呢右键给他在上方插入一行,然后呢在这个 a 一 单元格当中怎么样?他说要写一个期中考试成绩。好, 那这个是不是标题了?那标题呢?它还需要怎么样?它需要将 a 一 到 l 一 怎么样去合并单元格并居中,那我们怎么弄?我们选中鼠标 一直拖拖拖拖拖到这个 l 一, 我们这里呢有一个合并居中啊,那我们这个标题 a 就 可以进行合并以及 居中了。那还有常考的是什么呢?就是把这里,比如说我把这里的字体给它改一下,改成什么?改成等线啊,把它的字号改一改,对吧?然后呢把它的字体颜色啊,这里是颜色改红色, 这个都是我们常考的一些啊,还有呢比如说把它加粗啊,这里是加粗,这里呢是倾斜啊,倾斜,那 这个是我们的一些文字类型的一些操作。那还有是什么?比如我们的一个列宽行高,那比如说我想把这个考号这一列 啊,设置一下它的列宽,那我该怎么弄呢?首先把鼠标点击左键点击这个 a 这一列,然后呢右键给它选择列宽,比如说它题目当中要求十五,那我们就输入十五,然后点确定, 那这个列宽就设置好了,那行高呢?同样,假如说把这第二行给他设置一个行高,那同样点击这个行这一行号,然后呢右键行高啊,比如说二十, 那这个呢,就是我们的行高以及列宽。好了,那接下来呢,你看一下,假如说啊,我要算语文的这个平均分,怎么办呢?比如说我要算在这个单元格内平均分,是不是要使用到我们的什么函数 平均值吧,你看算平均值好,我们就可以点击确定。然后呢 语文是不是 c 三到 c 十三啊?你看是不是就可以点确定了? 那我这里是不是就算出来了我们的语文平均分呀?那我们同样我想算算数学,外语,物理,那我是不是怎么样 可以又自动填充呀?横着也可以填啊,横着也可以填,那这个,哎,填充完了,填充完了之后呢,我想怎么样?我想把它保留两位小数,那该怎么办呢?你看啊,我把它这个地方全部选中,然后右键 给他怎么样设置单元格格式,那我把这个格式设置为什么数值类型,然后呢小数位数,你看我可以怎么样 给他选择两位啊,或者三位啊?都可以确定,然后呢这样就可以了,那比如说你看他这个没有进行居中,对吧?那我就可以怎么样这里问水平居中啊,那这个呢?都是我们常考的一些点, 那同学们,咱们这道题呢?以及我们 excel 的 一些需要考试注意的事项就讲到这里。
8299王者风范zc 09:29
09:29 00:53查看AI文稿AI文稿
00:53查看AI文稿AI文稿发现一个特别适合发论文的方向,损失函数加自注意力机制。深度学习中,损失函数与注意力机制的结合正成为提升模型性能的关键方向。传统损失函数在处理类别不平衡或造声数据时存在局限,而注意力机制能动态聚焦关键信息,但可能忽视大局上下文。 通过将二者结合,可以引导损失函数更精准的优化模型注意力机制,识别重要特征损失函数锯子调整权重,从而提升模型鲁棒性和泛化能力。例如,在分类任务中,注意力加权损失可缓解样本不均衡问题。在噪声数据下,注意力引导的损失设计能减少溶于干扰。 这一协同优化策略为图像识别、自然语言处理等复杂任务提供了新思路,有望推动深度学习模型的性能边界。另外,我整理了十篇关于损失函数加自注意力机制的最新论文及代码,方便大家参考。
44芒果-论文指导 06:0231菜鸡的老黎
06:0231菜鸡的老黎 03:01查看AI文稿AI文稿
03:01查看AI文稿AI文稿这节课呢,我们来说一下 vivo 三的 set up 函数和 conversation api。 vivo 三呢,它引入 set up 函数和 conversation api, 标志着 vivo 的 应用构建方式的革新,它提供了一种更加灵活而模块化的代码组织方式,有助于逻辑赋用和状态管理。让我们深入探索 set up 函数和 conversation api。 首先呢是 set up 函数,它的位置和作用。那么 set up 函数呢?它位于组建的顶层啊,作为组建实力创建过程的一部分,被调用是 conversation api 的 入口点,目的呢,就是集中管理组建内部的逻辑, 包括响应式数据、计算属性、生命周期、钩子函数等等,为组建提供初步所需的全部上下文。那么返回值呢?就是返回一个对象,哎,该对象的属性和方法将被暴露给模板。使用 composition api 的 核心,首先一个呢是响应式 api, 它的 ref 和 reactive 是 用于创建响应式数据的。好吧,就比如咱们上一节课所说的那样。 还有就是生命周期钩子,像 on, before mount, unmounted, un updated, unamounted, 是 吧?这些函数代替了传统的生命周期。 另外就是组合函数,我们通过创建纯函数来调用逻辑,这些函数接收状态作为参数,返回新的状态或副作用处理逻辑。 那么 conversation 这个函数呢?它是允许多个逻辑片段组合在一起,形成组建特有的行为,提高代码的可读性和可维护性。 那我们使用 conversation 呃 api 和这个 set up 函数啊,上节课呢,我们也写了一个基本的势利,对吧?就是一个计数器组建,用 r, e, f 和 set up, 我们在 g 呃 gs 代码当中呢,是引入了 e, f, 然后可以去定义一个 count, 通过这个事件呢,去触发咱们 button 按钮身上的事件,从而让这个 count 进行加加。 那需要我们注意的就是在 setup 当中不能使用 this 关键字访问组建实力,那么所有依赖项呢,应该直接导入或者定义在函数内。第二个呢就是 compensation api 组建内的逻辑声明顺序是不影响它的执行逻辑的, 这是鼓励关注点分离和呃逻辑模块化,那模板中直接访问 set up 访问的对象属性,哎,不需要点 value 访问响应式属性。 总的来说呢, set up 函数和 compensation api 是 real 三的一个重要改进,它们推动了组建逻辑的模块化和可维护性。 通过集中管理响应式数据,生命周期钩子和逻辑片段,哎,让我们可以更清晰的去组织代码,哎,异于附用的和测试。 ok, 希望大家呢能够把这两点呢好好的去理解。
13前端高频面试题 01:39查看AI文稿AI文稿
01:39查看AI文稿AI文稿看下这道面试题,请实现一个生考背函数。近期需要前来面试的同学建议领取非面试宝典,查看一些工程画,甚至于画以及八卦纹都有生考背本质上是一个深度优先变现的过程。 简拷贝只负责指向堆堆层的指征,而深拷贝需要在堆堆层中开辟新的空间,完全复制一份新的数据结构。这里提供三个层级的方案,方案一,接受虚拟化凭证写业务。如果对象里全是刚刚进来的数据,没有函数 on the find 日期,直接用 接收点 pos 一 号代码搞定。虽然它很暴力,会把函数和 on the find 的 弄丢,也不支持循环引用,但处理 api 返回的纯接收数据够用了。如果环境允许,还可以用 struct 克隆 这个 api。 这也是我们的第二个方案,性能好,支持循环引用。第三个,递归叫 quickmap 方案,这是面试中含金量最高的写法,解决的循环引用和特殊类型的问题。 第一步,如果是基本类型,直接返回,这是帝国的出口。第二步,专门处理 data 和政策。很多同学面试挂在这是因为忘了这两位,不能直接变利,必须溜出来。第三步,我们要传入一个 wikmap, 这次拷贝前先看 map 里面有没有,如果有,说明这是个圈,直接返回,结果 给他转了。第四步, new target construct。 这招就要轻而易打力,不管你是宿主还是对象,找过这函数,拿个新的就行,这样连连勋章都继承过来了。最后用 delete on case 便利。为什么不用赋音呢?因为 delete 能把 simba 属性也拷走。
13前端架构师杰哥 10:44查看AI文稿AI文稿
10:44查看AI文稿AI文稿同学们好,下面继续进行复习,接下来请看第四题,函数 range 一 六产生一个列表,它是什么呢?那这道题呢,我们首先要搞清楚我们 range 函数 它的格式啊,它的语法,也就是我们括号里面有几个参数,你要知道它是什么样的含义,那我们来看一下 rand 函数里面有三个参数, 我们的初值,中值以及不长啊,那注意的是,我们的中值呢,它要到达中值之前就停止,它不包括中值啊,一定要知道不包括,那 我们来举几个例子来知道一下我们的 run 函数。首先 run 函数呢,我们里面啊写一个什么呢?根据它的格式来,比如说二,四, 哎一,那这样一个 range 函数呢?你看一对应,它是初值,它是中值,它是不长,那 range 函数呢?可以生成一个列表,列表用什么表示?是不是用一个中括号去表示呀?啊?中括号 列表,那我们的圆组呢?圆组用什么表示?是不是小括号啊?是圆组,那中括号,小括号都有了,那大括号呢? 是不是就代表的是集合啊?集合以及它是什么呢?也可以代表我们的字典啊。字典, 那你要搞清楚这几个他用什么样的符号去表示, 那这是一个列表,对吧?列表,列表里面有什么数呢?啊?他从二开始,哎,二开始,然后呢?用逗号隔开。第二个数是多少呢? 它是根据我们的不长来决定的啊,你看一下,我们不长为一,所以第一个数与第二个数中间相差一,所以呢?哎,它是不是三了,三了?好,那下一个第三个是不是有,有了 四了?哎,那我们看一下,我们这里说了不包括中指,所以呢,我们这里的四它能不能存在?它是不是不能存在?所以呢,我们这里啊,要怎么样 到四就停止了,所以这个列表呢?就是二三啊,二三,那这个就是我们的第一个例子,那接下来我们来看一下第二个例子, range 二十二呢?开始吗?是不是也是一个列表?从哪开始?二开始,哎,他不查为几,是不是 为二,那依次去增加二四、六 八,哎,然后到哪了?是不是到十了?但是我们的中指是多少?是不是十,所以没有那个十啊?所以呢,这边就是我们的一个 它所生成的一个列表,那大家看一下,我们这里题目当中呢,它只有两个参数,对吧?哎,那两个参数是什么样的意思呢? 他是省略了我们的不长啊,省略了不长,那我们省略不长之后,他的默认不长为一啊,默认不长为一。所以呢,根据这个规则来看,我们应该选什么?从一开始 到几结束,是不是到五结束?中间是相差一的,对吧?所以选择我们的 b 选项啊。 b 选项,那这个是我们的一个 range 函数,哎,那有的时候呢, 它还有一个参数的情况,比如说啊,我们的 range 就写一个六,那是什么意思呢?他是把我们的出值以及布长都省略啊,都省略,那默认的出值为零,所以呢,他这个应该是什么? 是不是从零开始啊?然后一直到结, 是不是到五啊?那这个就是我们的一个第四道题,下面我们来看第五道题,第五道题是一个阅读程序段,那首先我们来看一下第一行, 第一行是什么?是不是一条负值语句,将一的值付给了 s, 也就变成了一,对吧? s 变为一,那第二行呢?它是一个什么? 是不是一个 for 循环了啊? for 循环的开始,那这里首先有一个 range 函数啊,我们刚刚那道题所讲的,这里的 range 函数,它代表一个什么样的列表呢?是不是一个从零开始, 然后呢?不长为三,那第二个数是不是为三,然后呢再变六,然后呢?再是再是什么?再是九啊?那后面呢?是不是到到多少了? 到十二了,但是呢,我们是不是要到十就停了,所以呢,这个就生成这样一个列表啊,那也就是说我们列表已经求出来了,那这里呢,我们来看一下 这个负循环,它所代表的含义啊,它是怎么样运行的? 我们来看一下 for 循环呢?你看刚刚那个啊,一个 for 一个,这个叫什么?循环变量,那我们这里,哎,这里的 i 是 不是就是循环变量,对吧?那后面呢是一个 in, 是 一个关键字,然后呢一个列表, 那列表呢?我们刚刚已经算出来了,是不是零三六九,对吧?好,那接下来呢,他有一个缩进,缩进代表什么意思呢?他代表他这个缩进的语句,他是循环体。 什么叫循环体?也就是重复去做一件事情啊,重复所做的一件事,那 这样的呢,就叫做我们的循环啊, for 循环,那我们这里呢,这个例子,比如说 for i in 啊,一二三四五六七八九十,然后呢,这里是不是就是我们的循环体? 那循环体这是什么?这是不是一个输出函数呀?输出,那输出什么呢?哎,这里是个 i, 那我们循环体是重复所做的事情,那第一次我们爱的值为几呢?他是怎么来的呢?他是从这个列表当中去取啊,取列表当中的第一个,所以第一个是谁?是不是一,所以呢,他会输出一个一积分。 好了,那结束了之后呢?哎,这个循环体只有一条语句,对吧?结束了之后,他再回去啊,再去 执行第二次循环。那第二次循环呢?他还是从这个列表当中取,取谁了呢?是不是把这个值取到了二,所以呢,他会又会输出一个二积分, 依次类推啊,他会输出一积分,二积分,三积分,四积分,五积分,六积分,七积分,八积分,九积分,十积分。那这个呢,就是我们的一个负循环啊,负循环。 好了,讲完了这些呢,我们来看一下这一道题, i 是 不是就是循环变量? 那这个 rung 呢?它是一个列表,我们已经算出来了,那我们这个 i 每次循环,它从列表当中是不是都要取一个数出来 啊?第一次是不是取零?第二次呢,取的是三,第三次呢,取的是六,第四次呢,是不是取的是九,对吧?那我们循环题里面执行的是什么呢?循环题这个干嘛的? s 加等于 i, s 加等于 i, 哎,那这个呢,是我们的一个负值运算符啊,它的减写,它代表什么样的含义呢?它相当于 s 等于 s 加 i 啊,相当于 s, 等于 s 加 i, 那 第一次循环是不是 s 就 等于什么 s? 原来的 s 是 多少?是不是一?那加上一个 i, i 是 多少?是不是零?所以呢,是不是就等于一了? 好了,第二次呢?他又去取,那第二次 s 的 值为多少?是不是原来的 s 的 值为一,加上取什么取?是不是三?是不是就是四了?那第三次呢? 是不是 s 等于四,去加上六是不是等于十了?那第四次呢?是不是 s 等于 十?加九是不是等于十九了?哎,那好了,那到后面呢?我还去取,是不是九后面没有了。 那没有的话呢?那我们这个循环就停止了啊?循环停止了,那我们这一部分就是我们的循环。 那循环停止了之后呢?它干嘛了?是不是 print 一个 s 了?那 s 最终的值是多少?是不是就是十九?所以选择的是什么?是不是 b 选项?
5390王者风范zc 04:39查看AI文稿AI文稿
04:39查看AI文稿AI文稿还在为复杂计算头秃?这款卡西欧计算器来拯救你!从中学到大学,从考研到竞赛,从留学考试到职考取证,这款卡西欧计算器堪称你的数学神器,四种颜色可选,他身怀四百九十八种函数功能,绝技、解方程、算矩阵、岗位积分进至转换 你能想到的理科计算需求,他几乎都能满足。全国中学生物理竞赛、中国化学奥林匹克竞赛、周培元大学生历学竞赛都 推荐它。考研专业课、 iq i b 建造师考试也能靠它高效答题,把计算时间省下来,让你有更多精力思考。核心考点,双重电源纽扣电池加太阳能续航拉满附赠卡扣式外壳,防摔耐磨。还在为复杂计算头凸,这款卡西欧计算器来拯救你! 从中学到大学,从考研到竞赛,从留学考试到职考取证,这款卡西欧计算器堪称你的数学神器,四种颜色可选,他身怀四百九十八种函数功能,绝技、解方程、算矩阵、岗位积分、静止转换,你能想到的理科!
0米喵 07:00查看AI文稿AI文稿
07:00查看AI文稿AI文稿此题不会,高一期末考试必备,今天一期视频彻底讲清楚此类题型。好,我们来看一下咱们三角函数的单选压轴题,也是高一期末考试经常喜欢考的题。他说 f x 在 零到三分之二上存在零点, 在三分之二派到派上单调递增,让你去求 omega 的 取值范围。那这个题的话就分为两步走嘛。第一个是先算那个零到三分之派上存在零点,算出 omega 的 范围,再算三分之二派到派单调递增, 算出 omega 的 范围,取它们的交集就可以了呀。来一个一个来。首先先写一个 解,他说 x 属于零到三分之派,那我们 omega x 就 属于零到三分之派, omega 继续。然后呢,我们 omega x 加三分之派,它就属于三分之派到三分之派, omega 加三分之派就行了。好,我们把整体的范围已经表示出来了。接下来就是换元,零 omega x 加三分之派等于 t。 好, 那 t 呢?就属于三分之派到三分之派, omega 加三分之派,那我们这个式子就变成了 f g 就 等于 c e t。 换元之后呢,我们就可以画图像,通过图像来看一下什么时候它是存在零点的, 这是我们 c 音 t 的 图像,那我们的 t 范围是三分之派到三分之派,我们应该加三分之派,那好,那应该就是从三分之派往右找,什么时候存在零点,对吧?那我们找下三分之派,中间这个点是二分之派,那三分之派大概就在这。 那我们拿个红笔画一下,就是从这开始一直往后走啊,走到这的时候是存在第一个零点,对不对?那往后的话,他都存在零点了,所以我们这个 t 的 范围,他三分之派,欧米伽加三分之派,他最小,最小应该要是比这个派要大的,因为过了这个派这个点,他才能存在第一个零点。好,那我们可以写出第一个式子,就是 三分之派,欧米伽加三分之派,他应该是大于派的,但是注意注意这块能不能取等,如果取等, 这等于等,所以他这也能等于派,那他这能等于派的时候,但是他取不到派,那就说明从三分之派到取不到派的时候,他是没有零点的,所以我们必须要让他大于派, 所以在算的时候一定要注意取等条件啊。那这个可以算出来,三分之派欧米伽大于三分之二派,那我们就可以得到欧米伽是大于二的,是不是? 那所以呢,我们就在 ab 里面选,但是呢,这只是其中的前半句话的情况,然后还有后半句话说,在三分之二派到派上单调递增,那同样嘛,还是先算出它整体的范围, x 属于 三分之二派到派,那欧米伽 x 就 属于三分之二派,欧米伽到派欧米伽欧米伽加三分之派就属于三分之二派,欧米伽加三分之派到 派欧米伽加三分之派,这不就是它的范围吗?同样嘛,和上面那个过程一模一样,令 欧米伽 x 加三分之派等于 t, 那 t 呢,就属于三分之二派欧米伽加三分之派 pi 欧米伽加三分之派,然后呢,这个式则变成了 f t 就 等于 c n t, 那同样我们也要去画图像,好图像已经画好了,那这样的话,他要单调递增,对吧?因为咱们正弦函数是一个周期函数,所以我们只需要让他找出其中的一段 增区间,然后呢加上二 k pi 就 可以了。好,那我们一般都是取最小的就是负二分之派,负二分之派到 二分之派,他这一段是不是单调递增吗?对不对?他是单调递增的话,意思就说你这个 t 的 范围一定要在这个负二分之派到二分之派中间,可以去的吗?对不对?就是他的子集的时候,我们就满足他单调递增。好,那我们可以写出一个式子, 就是三分之二派欧米伽加三分之派,他应该是大于等于负二分之派, 然后呢派欧米伽加三分之派应该小于等于二分之派,就是他的中间,但是呢,这只表示的是其中的一段,我们的正弦函数是周期函数,对不对?所以我们还需要加上一个周期是二派派, 对不对?好,那我们解出这个式子就可以了。计算过程我就不写了,我们直接可以算出这个 omega 是 大于等于三 k 减四分之五,小于等于二 k 加六分之一啊,那到这一步的时候我们说过了,算出前面这个欧米伽范围,算出后面这个欧米伽范围,要取它的交集,是不是?那我们就给 k 要赋值了啊?当 k 写这吧,当 k 等于零时, 当 k 等于零的时候,那 omega 就 属于负的四分之五,然后到六分之一,是不是和第一步算出来这个 omega 大 于二,是不是没有交集?那就不行,来继续,当 k 等于一时,那 omega 就 属于等于一的时候,是四分之七到 二分之十三,那这样的话我们和前面就有交集了,前面算出来是 omega 大 于二,那后面算出来是四分之七到二分之十三,取交集之后, 所以欧米伽就属于二到二分之十三 b 区间,所以这个题选的是 b 选项,你学会了吗?
414烟花虽易冷
猜你喜欢
- 4215戈蓝V








