六年级下册数学光数学圆锥怎么做立体
六年级开学要准备的学具来了,透视几何体演示器结合课本第三单元,需要孩子借助教具来学习。圆柱和圆锥把圆柱展开是两个圆形和一个长方形,圆锥展开是一个圆形和扇形。 由此可以发现,长方形的长等于圆柱体面的周长等于圆柱的高,而同等同高的圆锥体三个正好能装满圆柱体。 这套透明几何能把复杂的图形平面化,培养孩子的思维和想象力。他还是通体透明的设计,可以让孩子各个角度观察,更加全面理解几何形状。家里有五六年级的孩子,提前准备上网。
粉丝3782获赞1.7万
相关视频
 00:25查看AI文稿AI文稿
00:25查看AI文稿AI文稿六下数学最难的圆柱和圆锥,就这六大题型,寒假练完稳进前三,可打印六下数学圆柱和圆锥六大题型加解析技巧专题一切专题二,消 专题三,融注专题四,增高减高专题六,旋转体应用题专项训练专项练习一、与圆柱表面积有关的实际问题与圆柱体积有关的实际问题与圆锥体积有关的实际问题以上均有电子版。
234菜菜爱学习 01:45查看AI文稿AI文稿
01:45查看AI文稿AI文稿这是一款小学生使用的圆柱与圆锥体积演示器,还原课本推导过程,包含了圆柱和长方体之间的转换,等底等高的圆柱。这是一款小学生使用的圆柱与圆锥体积演示器,还原课本推导过程,包含了圆柱和长方体之间的转换,等底等高的圆柱。 圆柱圆锥六合一演示器辅助学习六年级圆柱圆锥单元,学习圆柱的体积还原公式。推导过程立体呈现圆柱与长方体的相互转换,学习面动成体。
 00:24查看AI文稿AI文稿
00:24查看AI文稿AI文稿六年级下册数学学习圆柱与圆锥需要用到这款圆柱三合一演示器,打开里面包含圆柱演示器,一个十六等分圆柱表面积演示只三张 皮筋,两根面动成体器,一套快速旋转面动成体教材同步学具。
 00:56查看AI文稿AI文稿
00:56查看AI文稿AI文稿六年级下册数学学习圆柱需要用到圆柱三合一演示器,我们先把它打开,组装成一个圆柱,用皮筋做固定,用长方形的表面基纸包住,圆柱用胶带固定好。 还有上下两个底面积,圆柱是由三个面围成的,圆柱上下两个面叫做底面,圆柱周围的面上下底面除外叫做侧面。圆柱的两个底之间的距离叫做高。从上图我们可以看到, 圆柱的表面积等于圆柱的侧面积,加两个底面积的面积。打开这个圆柱的表面积, 得到的是两个圆形,一个长方形,所以圆柱的表面积是侧面积,加两个底面积。与教材同步。下个视频分享一下圆柱的体积。
 00:25查看AI文稿AI文稿
00:25查看AI文稿AI文稿六下数学最难的圆柱和圆锥,就这六大题型,寒假练完稳进前三,可打印六下数学圆柱和圆锥六大题型加解析技巧专题一切专题二,削专题三,溶注专题四,增高减高专题六,旋转体 应用题专项训练专项练习一、与圆柱表面积有关的实际问题与圆柱体积有关的实际问题与圆锥体积有关的实际问题以上均用电子版。
1097盈盈💯 02:07查看AI文稿AI文稿
02:07查看AI文稿AI文稿圆柱和圆锥的体积之间存在什么关系呢?哎,请说一说。等底等高,等圆柱体积是圆锥体积的三倍, 等比等高的圆锥体积是圆柱体积的三分之一。好,根据这种关系,我们出了很多的填空题,请看,一个圆柱削去八立方分米,正好削成一个与它 等比等高的圆锥,这个圆柱的体积是多少立方分米? 我们在读题的时候要牢牢的抓住关键词,等比等高。好, 等比等高的关系。圆柱体积是圆柱体积的三倍,见了倍子距,先找一倍数,三倍前面的得得,前面的圆锥体积就是以倍,而圆柱的体积就是 三倍。那么看三倍的圆柱,我要把它削成一个最大的圆锥,快看一看。 哎,看这幅图,那么这个圆锥的体积就是一份呀, 那么这个圆柱的体积就是三分呀,消去了几分呢?对,三减一,消去了两分,那么消去了八立方分米, 那么两分就是八立方分米,所以八除以二,是不是一分的体积呢?也就是圆锥的体积,而圆柱的体积是三分,再乘三。 好,就是这道题的答案。简单吧,理解了关系,我们做题就变得非常简单了。好,点个赞吧!
62燕子老师讲数学 00:40查看AI文稿AI文稿
00:40查看AI文稿AI文稿六下数学最难的圆柱和圆锥就这七大题型,寒假练完稳进前三,可打印六下数学寒假预习圆柱与圆锥计算公式,圆柱,圆柱的底面积等于 s 圆,圆柱的侧面积等于底面周长乘高圆柱的表面积等于圆柱的侧面积加底面积乘二 圆锥公式拓展应用图七、问题圆柱形物体表面积问题圆柱的体积问题圆柱的体积问题圆柱、圆锥转化问题 圆柱和圆锥常考题型归类类型一,圆柱侧面积、表面积的实际应用类型二,圆柱、圆锥表面积增加或减少的实际问题类型三,圆柱、圆锥的等级变形问题类型四,有关长方形和圆柱的问题类型五,稍复杂的等级变形问题类型六,旋转体问题类型七,瓶子容积问题以上均有电子版。
422盈盈💯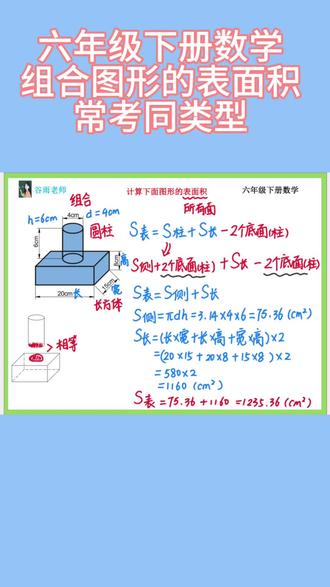 04:11查看AI文稿AI文稿
04:11查看AI文稿AI文稿同学们好,我们来看这个题,计算下面图形的表面积,那么如图所示,这是一个组合图形,那么这个组合图形的上面呢,是一个圆柱,而这个组合图形的下面呢,是一个长方体, 那么现在要求这个组合图形的表面积,我们先思考一下什么叫做表面积,围成立体图形所有面的面积之和。好,那么很多同学呢,会想到, s 表就等于圆柱的表面积 加上长方体的表面积,但是大家想一想,在这个组合图形当中呢,这个面圆柱的这个底面是被遮住了的, 而长方体当中也有这样的一个面被遮住了,这两个面有什么关系?这两个面相等,并且都是圆柱的什么面?圆柱的底面,所以因为被遮住了,所以咱们还要减去两个 底面,这个底面啊,是圆柱的底面。接着这个式子咱们就可以进行进一步转化,圆柱的表面积等于 s 册 加上两个底面,对不对? 那么长方体的表面积呢?咱们就直接进行计算就可以了,这个式子咱们就可以进行进一步推导。 好,现在大家观察,加上两个底面减去两个底面,实际上就被怎么了?就被相互抵消了嘛,这两个部分就被相互抵消了,那实际上 s 表就怎么求? s 表就等于 s 测圆柱的侧面积加上长方体的表面积就可以了。接着咱们来根据题目当中的已知条件,分别求出侧面积和长方体的表面积就可以了。那么 s 测 圆柱的侧面积就等于派 d h。 好, 我们现在来找已知条件, d 圆柱的底面直径 d, 那 么等于四厘米在这里高呢? h 等于六厘米,所以代入式子就等于三点一四 乘四,再乘六,那么就等于七十五点三六,单位是平方厘米。那么长方体的表面积 s 长就等于长 乘高,加上长乘高 的和再乘二。好,现在我们来看,二十厘米是长方体的长,而这里的十五厘米是长方体的宽, 那么八厘米是长方体的高,所以咱们直接代入,也就是二十乘十五,加上二十乘八,加上十五乘八的和再乘二, 那么就等于五百八十乘二,等于一千一百六十平方厘米。好,现在我们来求表面积 s 表就等于 圆柱的侧面积,那么就等于七十五点三六,加上一千一百六十,就等于 一千二百三十五点三六,带上单位平方厘米。
138谷雨老师 04:30查看AI文稿AI文稿
04:30查看AI文稿AI文稿圆柱圆锥表面积体积演示器来了!六年级同步教材课堂学习专用!圆柱表面积演示圆锥表面积演示圆锥圆柱体积演示第一杯、第二杯、第三杯。 圆柱圆锥表面积体积演示器来了!六年级同步教材课堂学习专用!圆柱表面积演示圆锥表面积演示圆锥圆柱体积演示第一杯、第二杯。 圆柱圆锥表面积体积演示器来了,六年级同步教材课堂学习专用!圆柱表面积演示圆锥表面积演示第一杯、第二杯、第三杯。 圆柱圆锥表面积体积演示器来了!六年级同步教材 课 抖音 抖 音。
0恩恩 14:53查看AI文稿AI文稿
14:53查看AI文稿AI文稿看最近一段时间呀,我们一直在研究和圆柱、圆锥有关的问题, 刚才那节课,我们通过实验发现了圆柱、圆锥在等底等高的情况下,它们体积之间的关系呀,是这样的,圆柱的体积是圆锥体积的三倍, 而圆锥的体积呢,是圆柱体积的三分之一。淘气在学完了刚才的内容后啊,也有了自己的想法,我们一起来看看。 淘气说,把圆柱体削成一个和它等底等高的圆锥体,削下的体积是圆锥体的三分之二。 同学们,你们同意淘气的想法吗?把你的想法用喜欢的方式表达出来,让我们一起和同学交流一下你们都是怎么想的吧。 先来看第一位同学的,我是用射术的方法来解决问题的,因为圆锥和圆柱等底等高,所以我先射它们的底,面积都是六平方厘米,高都是六厘米, 那么圆柱的体积就等于三十六立方厘米,圆锥的体积等于十二立方厘米。 淘气说,圆柱削成圆锥,削下部分的体积就是圆柱体的三分之二。通过计算,我发现圆柱体的体积的三分之二是二十四立方厘米, 用圆柱体的体积减去,圆锥的体积也刚好等于二十四立方厘米,所以淘气的说法是正确的。还有的同学啊,是用了不同的方法也解决了这个问题,让我们快来听听看。 我同意淘气的想法,我是用画线段图的方法解决问题的,因为是把圆柱削成一个和它等底等高的圆锥,所以我把圆锥的体积看成一份, 圆柱的体积就有这样的三份,也就是说圆柱的体积比圆锥的体积多两份,这两份就是削下的体积,所以削下的体积是圆柱体积的三分之二。 我还想到削下的体积是圆锥体积的两倍,你不仅解决了这个问题,还有了自己进一步的思考。大拇指啊送给你,下面我们再来听听后面两位同学他们是怎么想的吧! 我同意淘气的想法,因为圆柱和圆锥等底等高时,微锥等于三分之一,微柱如果微柱是单位一,那微锥就是它的三分之一,那削掉的部分就是一减三分之一,也就是圆柱的三分之二。 同学们,让我们把刚才三位同学的做法放在一起,再来看一看,它们的结果是相同的,但所用的方法却不一样, 无论是设数还是画图,还是寻找数量之间的关系,这些都是我们研究问题,解决问题的好帮手呢。 好了,同学们,我们来看一看。刚才我们对圆柱、圆锥在等底等高时,体积之间的关系进行了深入的讨论。那同学们,如果让你继续思考, 你还想研究点什么呢?能提出什么问题吗? 我想研究圆柱和圆锥的底面积,高体积之间还有没有别的关系呢? 我来帮你补充。我们已经研究了圆柱、圆锥在底面积和高相等的情况下,体积之间的关系。 如果是体积相等,底面积也相等,圆柱和圆锥的高会是怎样的呢?如果是体积相等,高也相等,圆柱和圆锥的底面积又是怎样的呢? 这真是一个好问题啊!同学们,你们听清楚刚才那位同学也提出的问题了吗?那你准备用什么方法来研究呢? 对刚才我们用到的设数画图,寻找数量之间的关系,是不是能够帮助到你呢?让我们来听听同学们是怎么研究这个问题的吧! 我是用设数的方法研究的,先假设圆柱和圆锥的体积都是十,底面积都是二,再分别求出圆柱和圆锥的高。利用公式我计算出圆柱的高等于五,圆锥的高等于十五, 然后用圆柱的高和圆锥的高作比较,发现三个圆柱的高等于一个圆锥的高。接下来我又设了两组不同的数来找圆柱高和圆锥高的关系,得到的结果和刚才是一样的, 所以我的结论是,圆柱的高等于圆锥高的三分之一,也可以说圆锥的高等于圆柱高的三倍。同学们,你们听清楚这位同学的想法了吗? 他最难能可贵的地方啊,是当他设数找到了圆柱高和圆锥高之间的关系后啊,没有急于下结论,而是又设了两组数来验证自己的想法是否正确。 像他这样严谨的研究问题的态度啊,特别值得我们大家学习。当然,我们在说自己结论的时候,别忘了把重要的信息说在前面,那就是在圆柱和圆锥 体积相等,底面积也相等时,它们的高之间的关系是这样的。还有谁也是用了射术的方法研究了刚才同学们提出的第二个问题呢?让我们一起来听听看。 老师,我也是用了射术的方法,先分别假设圆柱和圆锥的体积是十十八六, 高是五九六,然后再分别计算出圆柱和圆锥的底面积,我发现结果也都是一样的, 所以我得出的结论是,当圆柱和圆锥体积相等,高也相等时, 圆柱的底面积等于圆锥底面积的三分之一,也可以说圆锥的底面积等于圆柱底面积的三倍。两位同学用设数的方法分别研究了刚才同学们提出的那两个问题, 还有没有同学是用其他方法也研究了这两个问题呢?让我们一起来听一听下面这位同学他是怎么想的? 我解决这个问题,用了公式推导的方法,因为圆柱的体积和圆锥的体积相等,根据体积的计算公式,我列出了这样的等式, s 柱乘 h 柱等于三分之一, s 锥乘 h 锥。又因为圆柱和圆锥的底面积相等,根据等式的性质,等式两边同时除以相同的数,零除外,等式不变。我把等式两边同时除以底面积, 就得出了圆柱高和圆锥高之间的关系,就是 h 柱等于三分之一 h 锥,也可以说成 h 锥等于三 h 柱。第二个问题也是用了同样的方法得出了圆柱底面积和圆锥底面积之间的关系。是这样的, 同学们,你们听清楚了吗?几位同学虽然用的方法不一样,但是得出的结论是相同的,让我们一起来看一看。 刚才同学们通过设数和公式推导等方法,发现圆柱和圆锥在体积相等,底面积也相等的时候,它们之间的高是怎样的?对, h 柱等于三分之一 h 锥, h 锥等于三 h 柱,那圆柱和圆锥体积相等,高也相等时,它们的底面积之间又有怎样的关系呢? 没错, s 柱等于 s 锥的三分之一,而 s 锥呢,是 s 柱的三倍。 再把我们刚才那节课找到的发现的规律啊放在一起,我们来看一看。 同学们,我们今天通过实验、设数、公式推导等方法,研究了圆柱、圆锥底面积高体积之间这三组关系,同学们,你们都学会了吗? 那让我们来看看笑笑又给我们带来了什么问题吧。 圆柱和圆锥的体积相等,底面积也相等。如果圆锥的高是六厘米,那么圆柱的高是多少厘米呢? 刚才我们研究问题时用到的方法能帮助到你吗?让我们来听听同学是怎么想的。 笑笑提出的问题,虽然不知道圆柱和圆锥的底面积和高, 但是我们可以用体积相等,底面积也相等时,圆柱的高是圆锥高的三分之一来解决这个问题。 只要用圆锥的高六厘米乘以三分之一,就能得到圆柱的高是两厘米了。 看来呀,当我们掌握了圆柱、圆锥底面积、高体积之间的关系,还真能解决不少和圆柱、圆锥有关的问题呢。那让我们快来看一看 草原上的牧民叔叔又给我们带来了什么问题吧。一个蒙古包由一个圆柱和一个圆锥组成,这个蒙古包所占的空间是多大? 要想解决这个问题,同学们我们需要怎么做呢? 这个蒙古包的上面是一个圆锥,下面是一个圆柱,所以我先分别求出圆柱和圆锥的体积,再相加,得出二十一乘三点一四,也就是六十五点九四平方米。 刚才这位同学呀,把蒙古包分成了两部分,分别求体积再相加,求出了蒙古包的空间有多大这个问题,那还有没有同学是用别的方法也解决了这个问题呢?让我们一起来听听看。 我想用今天研究的柱锥之间的关系解决问题。我发现圆锥和圆柱的底面积是相等的,圆柱的高是圆锥高的两倍,于是我先求出圆锥的体积是九点四二毫米, 然后我把大圆柱平均分成两份,这个圆柱和圆锥等底等高,所以体积就是圆锥的三倍。 而大圆柱里有两份就是三乘二,等于六分,这样整个蒙古包就有六加一,一共七份。再用七乘九点四二就求出蒙古包的体积是六十五点九四平方米。 同学们,你们听清了吗?刚才那位同学呀,他不仅关注到了圆柱、圆锥等底等高时体积之间的倍数关系, 还想到了大圆柱的高和圆锥高的倍数关系,从而巧妙的解决了这个问题。 淘气呀,也想用这种方法来解决蒙古包体积的问题,快来看一看。哎,它的结果和刚才两位同学的结果不一样呢,你能发现淘气的问题出在哪了吗? 我发现淘气是把圆柱部分的体积看成圆锥部分的三倍, 可是只有在等底等高的情况下,圆柱的体积才是圆锥的三倍。他并没有注意到圆柱部分的高是两米,而圆锥部分的高是一米,他们并不等高,此时圆柱体积应该是圆锥体积的六倍。 哇,你真厉害,一下就发现了淘气的问题所在呢。那看来要想很好的解决这个问题,我们要关注到圆柱圆锥高的变化呢。同学们,回顾一下今天我们的学习过程, 通过今天的学习,你有什么收获?今天我们是用什么方法来研究圆柱和圆锥之间的关系呢? 相信同学们一定也积累了不少解决问题的经验吧,如果让停课不停!
 00:31查看AI文稿AI文稿
00:31查看AI文稿AI文稿大红老师在视频当中介绍了六年级下的重点章节圆柱与圆锥,而圆柱与圆锥最常用的公式,老师帮你整理了一份。 除了公式之外,我们还讲了几个专题,分别是切削融。今天介绍一个切的专题,一招公式解决掉汤。
199大宏老师讲数学 02:31查看AI文稿AI文稿
02:31查看AI文稿AI文稿大家好,我们看这道题,圆锥容器中有十升的水,那在哪里呢?就是我们的下面这部分的小圆、小圆柱,小圆、小圆锥,所以我们用小圆锥这样来表示, 如果小圆锥的高为 h, 那 大圆锥的高, 因为小水的高度是圆锥高度的一半,所以大圆锥的高就是二 h。 然后我们再从这个图当中能够看出来小圆锥的底面半径,如果是一大圆锥的底面半径就是二, 一个是半径是二,一个是半径是一,它的底面积就是一比四, 这是底面积的关系,所以我们小圆锥就可以看成是它的体积可以看的是一底面积是一乘上高,我们假设高也等于 h 等于一, 再乘三分之一等于三分之一。而我们大圆锥的体积, 它的底面积就是四乘上高是二, 那么再乘三分之一就是三分之八。然后题目教我们求的是什么呢?题目教我们求的是还能 装多少升的水,装的是哪一部分?是上面这部分,所以上面这部分就是大圆锥的体积,减去小圆锥的体积就是我们上面所谓的圆台,就是三分之八,减 去三分之一,那么就等于三分之七。所以说上面能装三分之七,其中三分之一所对应的就是十升, 那么三分之七还能装三分之七,对应的就是十乘七等于七十升,所以这里就是七十升。那这道题就讲到这里,再见。
4龙哥 02:35查看AI文稿AI文稿
02:35查看AI文稿AI文稿包含了圆柱和长方体之间的转换等。底等高的圆柱圆锥可以演示三倍容积,借助教具,孩子更容易理解推导公式。 这款圆柱圆锥体积表面积演示器采用 pvc 材质制作而成,包含多种圆柱圆锥展示模具,与小学六年级课本内容完美契合,有了它,孩子能够直观的理解并掌握相。
0贸易百货






