福州一检数学解析几何压轴

那本期视频的话呢，讲解一下本次福州市一剪卷的两道几何压轴题，其中第十六题我们在考前的一剪冲刺复习一当中原原本本讲过的，那么用函数法求最值，大家可以参照一下之前的资料，那这边不再赘述了哈， 下面来看一下这个二十五题，简单把条件捋一下，这是一个等边三角形，那么异正 b o 垂直平分 a c。 之前给你们着重讲过，一定要两个点到线段，两段距离相等，这个过程一定要写出来， b a 等于 b c o a 等于 o c， 对 吧？那么这个时候既证明呢，它是高线，也能得到这个特殊角。 角距等于 a d e， 我 们可以用几何标记 r 相等等弧对等弦对等角，所以这两个角可以同时标上背塔。 由于这个是三十度加 r， 这个也是，所以等角对等边第一步就正反了。既然等幺三角形，那么三线合一，这个 e p 将垂直平分 b d， 所以说根据平行线所夹的线段成比例，即可证明 mn 为中位线。第三，很多人说这个辅助线不知道怎么添加，那实际上不需要添加辅助线，你们可以听我讲解一下，为什么 a e 比去 b e 涉及到这个三角形，我们刚才知道阿尔法加贝塔是六十度，对吧？那么这个 e a b 也是贝塔， 因为这个角是一百二，对吧？四边形对角互补，所以说 a e b 与这个 e m b 相似，同时两直线平行，我们可以在 a d e 这个地方标上背他，所以说 a e 假设这个点是 i a e i 和这个 b a e 也是一对拇指相似， 那我们在假设参数的时候，以小不宜大，对不对？本题没有具体的线段长度，肯定要设参数，不妨设这段为 m， 这段为 n， 那 a e 比去 b， e 等于 m 比 n。 第一步正过 b， e 等于 e d。 大 型的几何综合题跟你们讲过，要步与步之间逻辑给大家关联一下，所以我们可以把这个 b e 换成 e d， 于是就得到了 a e 比去 e d 等于 a， e 比去 e d。 这边又是一对母子相似，它将会等于 a i 比去 a d， a d 呢，也是等边三角形边长的一半，所以跟这个 n 是 一样的，我们可以标上 n， 从而证明了 a i 等于 m， 那 么 m i 呢，就可以用 n 减 m 来表示，因为这个 m 是 终点嘛。 接下来可以用这对八字形相似啊，也叫 x 形相似。 i 这个交叉地方构建出一个等式， m 比去 n 等于 n 减 m 比去 m， 接下来交叉相乘参数换算一下即可求出这对比例，所以说特别简单，也不需要做任何的辅助线。最关键的是要用啊，我教大家的这种 几何标记法。只不过这种压轴题呢，更加重视综合的标记能力，既要重视到角度，也要重视到边之间的关系，相互之间是形成了一个整体好，因为在相似当中，角跟边的关系是非常密切的，通过等角找到相似，再切换相似笔， 这也是相似等比代换当中的一种压轴。那么在微窗底当中有详细的这块内容的介绍。

这次福州一届的第二十五题，最后一问，我们应该如何突破呢啊？第二十五题，其实这是没有考大招技巧，考的是大家扎扎实实的基本功啊，和中考的亚洲题呢，其实非常接近哈， 那前两问难度不大，不用花太多的时间，大部分同学哈，稍微思考就可以解决了。那最后一问呢，其实他的特征呢，也非常明显，题干中呢，没有给线段的比值，我们就用色双元求比例。 那这一题呢，还有用到的方法，包括我们非常重要的一个就是解三角形啊，什么是解三角形呢？一个三角形当中如果有已知的边或角，有三个条件啊，那我们就可以求其他的边或者角啊，那具体怎么做，辅助线怎么求呢？哈，初中只有唯一的一个办法 做垂直啊，那这一点呢，在我们的几何题当中啊，是反反复复非常高频的出现的啊，所以对应的这个解三角形的方法，大家一定要掌握。 那这是一道几何综合题啊，做这道题呢，还有我们要求一些其他的基本功，比如说包括圆倒角，还有相似三角形的判断和性质啊，那相似三角形基本上也是我们压轴题当中必考的，那我们平时呢，最好按照专题 进行深度的训练，这样子考试的时候呢，思路会更加清晰啊，那对应的专题像设双圆，求比利，还有呢，解三角形，圆倒角、圆压轴，相似三角形压轴专题等等哈，我这边都有整理好的专题啊，有文档，有视频， 如果说考后或者说寒假有兴趣进行突破的，可以说一下二十五，或者呢和我这边进行沟通交流。

又考了又考了，他又考了，色双元球比例啊，今天福州一减的压轴题的最后一题，第二十五题的最后又问了哈，考察的就是我们的色双元球比例啊， 这个色双元球比例呢，在我们的二零二二年的福建中考考过，然后去年的福州一减二减啊，他也考过，你看今年的福州一减，他又出来了。 这类题呢，其实它的特征非常明显，它题目当中呢，没有给你任何具体的线段的长度，然后呢，叫你求两个线段的比值啊，那我们说它像这一题啊，它叫你求 a e 比 b e 嘛， 题目没有给你任何具体线段的长度，那你不可能求出 a e 和 b e 的 长，对不对？我们就可以设 a e 为小 a， 然后呢？ b e 为小 b， 然后呢想办法列出小 a 跟小 b 的 一个式子啊，就可以了。那列这个式怎么列呢？我们一般说通过勾股定律啊，相似啊，或者三角函数，那相似用的是最多的， 找到他们的一个等式，那两个字母一个等式，我们就可以求出它的比例了哈，所以说这个叫做色双元求比例，大家一定要掌握这一类题对应的答题方法呀。然后这一类题呢哈，我有专门的这个色双元求比例的专题，总共有十六道题， 那大家通过把这十六道题练透啊，我相信你对这类题啊哈，会比较有深刻的理解，考试的时候呢，就不会说无从下手了。那有想练习的同学啊，可以跟我说一下哈，我这边沟通一下，或者说一下射穿圆球比例。

哈喽，同学们大家好，欢迎观看助力老师的课堂之初三一减之二次函数压轴题系列，本期视频带你从题干入手，从读题再到画图，再列式再列，答案一气呵成！点赞加关注，我们马上开始！好，首先来看第一题，二次函数的压轴题， 我们直接读题就开始做啊，不需要过多的思考。已知抛物线 y 等于 a， x 平方加 b， x 经过 ab 两点，而 ab 两点的坐标已知，那 a 点是不是应该满足这个方程？所以我们的第一个设置是不是就可以得出，把 a 点的横坐标带进去？横中坐标一是不是应该等于 a 乘以负一的平方，也就是一，然后呢，再加上一个 b， 第二个 b 点带进去四是不就应该等于四？ a 加上二 b？ 由此通过计算，我们就可以知道， a 等于一， b 等于零。所以这个二函数的解析式是不是就变成了 y 等于 a 为一， x 平方就没了？这是第一题。再看到我们的第二题， 第二题说我们有一条直线， y 等于 k， x 加 t， 其中 k 和 t 是 常数， k 不 等于零与抛物线有且只有一个公共点是一撇 c， 那 我们可以大致的把这个抛物线和 e 参数放在一起， 那这个抛物线是 y 等于 x 的 平方，那我们把它画出来就应该是这样，我们把它画出来就行了。 y 等于 k， x 加 t， 它向上还是向下？我不用管它，因为它只有一个焦点是 c c 点， c 点的坐标是一撇 c， 那 由我们画的图，我们就应该知道这个 c 点是不是既在二函数上，又在这个一函数这条直线上，既然它在二函数上，那我们是不是可以把我们 c 点的坐标带入二函数？那我们将 c 一撇 c 带入二函数的解析式， y 等于 x 平方，那我们是不是就可以得出 c 等于一的平方也就等于一？所以我就可以知道 c 点的坐标是一撇一好， c 点的坐标是一撇一。已知以后，现在 c 点又在我们直线 y 等于 k， x 加 t 上，那由此我们就可以得出，把 c 点带入 y 等于 k， x 加 t， 是 不可以得出一等于 k 加上一个 t 好， 得出这个式子以后，那是不是可以得出 t 等于一减 k， 由此 y 等于 k， x 加上一个 t， 是 不是就变成了 k， x 加上一再减 k。 看我们从原来有两个未知的未知的字母变成了只有一个未知的字母，是不是就大大的简化了我们的这个解析式？ 同时要看到现在有了一个公共点， c 点的坐标已经用完，但是题上还有一个条件，有且只有一个公共点，那我们读到这里是不是就应该知道他们有公共点，有焦点就干嘛就连利吗？那我们将一参数 y 等于 k， x 加上一减去 k 与 y 等于 x 平方连立起来，他们只有一个共点，说明是不是只有一个解。那现在这个是指我们整理一下左边和左边相等，右边和右边相等，是不是可以得出 x 平方等于 k， x 加上一，再减去个 k？ 因为它只有一个解，所以我们整理一下 x 平方减去 k， x 减去一，加上 k 等于零，这是一个解，说明德尔塔等于德尔塔， b 平方减四 a， c， b 为负 k， 负 k 的 平方减去四倍的 a， a 为 x 平方的系数一，然后呢，再乘以 c， c 是 负一，加上一个 k， 它就要等于零。好，我们整理得出 k 平方，然后呢，减去一个四 k， 再加上四等于零，由此可知， x 减去哎， k 减去二的平方是不等于零，所以得出 k 等于二， k 等于二。现在我直线的方程是不是就变成了 y 等于二 x， 然后呢，加上一减去一个 k， 也是加上一，减二也是减一的形式。那这样一二题我们是不是就成功的解决了出来？ 好，再看到我们的第三题，第三题，也就是第二个小问，他说将直线 l 向下平移两个单位长度得到 l 一 撇，那 l 一 撇 的解析式我们是不是可以表示出来？读一句，写一个 y 等于二， x 减一，是 l 向下平移两个单位长度左加右减，上加下减，是不直接减二，那所以它就变成了 y 等于二， x 减三，这是 l 一 撇， 然后呢，再读第二句过点。 a 的 直线与抛物线的一个焦点是 d， 那 相当于说这条直线与抛物线交于一个点，是 a 点，负一撇一，一个焦点是 d 点，那 d 点的坐标不知道有焦点，也就是相交相交就怎么 直接连，所以直接将这个 m 这条直线 y 等于 r 减一倍的 x 加上一个 r， 与我二函数 y 等于 x 平方进行连立。连立完以后，是不是可以得出 x 平方等于 r 减一倍的 x 加上 r， 再次整理 x 平方，减去一个 r， 减一倍的 x， 减去 r 等于零。那现在有什么用呢？连立好以后，它有两个焦点，那这两个焦点的横坐标是不就应该是这个方程的解，因为这个方程是关于 x 的 方程。那 x 一 加 x 二， x 一 加上 x 二，是不就应该等于负的 a 分 之 b， a 为一， b 为负的 r 减一，所以负的 a 分 之 b 就 应该是 r 减一， 而这个横坐标，一个坐标是不是 a 点的坐标，一个坐标是不是 d 点的坐标？也就是说 x a 加上 x d 等于 r 减一，而 a 点的横坐标为负一，所以我们带进去负一加上 x d 等于 r 减一，那我就知道 d 点的横坐标是不应该等于 r， 所以由此我们就可以知道 x a 加上 x， d 等于 r 减一，所以 x d 等于 r， 那 x d 等于 r 有 什么用呢？因为我有焦点是地点，所以我选择把地点的坐标表示出来。那所以地点的坐标横坐标为 r， 重坐标为多少？因为地点在抛物线上， 因为 d 点和 a 点是焦点，焦点既在抛物线上，也在直线上，所以我把横坐标为 r 带进去，那重坐标就应该为 r 的 平方， 因为它满足 y 等于 x 平方，也就是重坐标等于横坐标的平方。好，这是 d 点，我已经求了出来。好，这是第二句，我们已经用完，再看第三句。过点 b 的 直线，这条直线与抛物线交于 b 点和 e 点， b 点的坐标是二撇四。用相同的方法是不是可以把 e 点的坐标求出来？所以连力连力， y 等于 s 加二， x 减去二， s 与 y 等于 x 平方。 老师直接整理了哈，所以 x 平方减去一个 s 加二倍的 x 加上二， s 等于零，同理可得。那 这这个等式算出来的是不是应该是 b 点和 e 点的 x 坐标？也就是说 x， b 加上 x， e 就 应该要等于负的 a 分 之 b， 也就是 s 加二。由于 b 点的横坐标为二，所以 e 点的横坐标是不是应该为 s？ 所以 我可以得出 e 点的横坐标为 s。 重坐标呢？ e 点同样在抛物线上，所以 e 点的重坐标为 s 的 平方， s 平方。好，这样我们的这一句话也已经用完了，你看我们压根就没有怎么思考，就是他说了什么有相交，我们就列个等式，把相应的坐标给它求出来。再看。当直线 m n 的 焦点 p 在 定直线上时，好，直线 m n 的 焦点， 现在我是不是就需要 p 点 m 点的 m， 直线的解析式是它， n 直线的解析式是它。那我把它们连立，是不是就可以求出 p 点的坐标？那我们连立出来， y 等于 r 减一倍的 x 加上 r 与 y 等于 s 加二倍的 x 减去二 s 进行连立，是不是就可以求出 p 点的坐标？那我们来求一下，我们放到上边来。 既然它们俩相等，说明左边是 y 和 y， 右边 r 减一倍的 x 加上 r， 是 不是就应该等于 s 加二倍的 x 减去个二 s， 那 我们把有 x 的 放在一边，没有 x 的 放到一边， 那有 x 的 放到一边，是不是就是 r 减一倍的 x 减去 s 加二倍的 x 等于负二 s 减去一个 r。 好，得出这个以后以后再整理一下。所以就是 r 减 s 减去三倍的 x 等于负的二 s 减去八。所以我的 x 是 不是应该等于 r 减 s 减去三分之负二 s 减去八。我们分子分母同时给它乘一个负一，是不是得出二 s 加上 r， 除一个 s 减去 r， 再加上一个三。好，现在我们就可以把 p 点的横坐标写出来， s 减 r 加上三分之二 s 加上一个 r， 这是 p 点的横坐标，那我们还需要谁呢？我们还需要 p 点的纵坐标，由于它的横坐标，已知纵坐标怎么办呢？ 那重坐标是不是把横坐标 x 任意的带到其中一个人里边去？比如说我们带到第一个，那 y 是 不是应该等于 r 减一去乘一个 s 减 r 加上三分之二 s 加上 r， 再加一个 r， 那 y 是 不是就可以直接解出来？我们通一个分就行了，是不是就变成了 s 减 r 加上三分之 r 减一去乘一个二， s 加上 r， 而后边这个 r 我 们是可以给它乘一个 s 减 r 加上三，再除一个 s 减 r 加上三。 那现在我们把这个式子整理一下， s 减 r 加上三分之二 r， s 加上 r 平方减去二， s 减去 r， s 减去 r 平方，再加上三 r， 那 我们消一下 负 r 平方， r 平方消掉，所以我们整理为， s 减 r 加上三分之三倍的 r， s 减去一个二 s 再加上一个二 r。 好，得出这样的设置， s 减 r 加上三分之三倍的 r， s 减去二， s 加上一个二 r。 好， 看似很复杂，好，看似很复杂， 实际待会我们来看得出了这个以后，那我们把这个擦掉，这句话已经用完了。好，现在是我们读题读出的这些信息， 试探求直线 d， e 是 否过定点，由于题上告诉我们 p 点在定直线 l 一 撇上，那 p 点是不是就应该要满足 l 一 撇这个解析式，所以我们把它代入就可以得出， s 减 r 加三 分之三倍的 r， s 减去二 s 加上一个二 r 就 应该等于二倍的 x 也是二去乘以个 s 减 r 加上三 分之二 s 加上 r 再减去一个三的形式好，得出它以后，我们是不是可以方程的两边同时乘以这样一个分母？是不是可以得出？ 老师把它写到上面，三倍的 r， s 减去二 s 加上二 r 等于四 s 加上二 r 减去三，乘以它是不是三 s 加上三 r 再减去一个九的形式好，得出它以后，那我们来削一下， 那现在我们如果消一下，是吧得到三倍的 r s， 然后呢？这里是 一个 s， 那 一个 s 减过来是减去三倍的 s， 然后呢？这里是减去一个三 r 再加上一个九，是不是就应该等于零？好，得出这个以后，是不是可以得出三倍的同时除以一个三吗？ r s 是 不是就应该等于 s 加上 r 再减去个三的形式好，由此可以得出， r s 等于 s 加上 r 再减去一个三。好，现在我们又做了一步，也是通过这一句话再用了一步探求 d e 是 否过定点，那要求 d e， 那 么已知 d 点的坐标是 r 撇 r 平方， e 点的坐标呢？是 s 撇 s 的 平方。那我们是不是可以把 d e 的 解析式给它表示出来？那 d e 的 解析式表示出来为多少呢？ y 减去 r 的 平方等于 k， k 是 s 平方，减去 r 平方，再除以 s 减 r 倍的 x 减去个 r， 你 可以用代练习算法来解哈，这个不难，所以就可以得出， y 减去 r 平方等于那上边 s 平方减 r 平方，是不是写成 s 加加乘以个 s 减 r， 也就是 s 加 r， 再乘一个 x 减啊？那我们把它展开，是不是就可以得到 y 等于 s， x 减去 s r， 然后呢？再加上一个？哎， 那我们是不是就可以得到 y 等于 s 加 r 倍的 x， 然后呢？减去 r s 减去 r 的 平方，再减去 r 的 平方， 再加上 r 的 平方，那后边刚好消掉，所以 y 等于 s 加上 r 倍的 x 减去 r s。 好， 得出这个以后，那我们要看喽，这里是 s 加 r， 而这里呢是 r s， 那 怎么办？那是不是这里再把它转化一下？那我们是不是可以得出 s 加上 r 等于 r s 加上一个三？ 那我们把 s 加用 rs 加三代替一下，是不是就 y 等于 rs 加上三倍的 x， 再减去个 rs？ 由于要过定点，那要过定点就要和谁无关呢？是不是就应该需要和 rs 没有关系？比如说无论你的 rs 等于多少，哦，我 照样过这个点，所以我们可以把这个式子进行整理。 y 等于什么呢？ r s 倍的 x 加上三 x， 再减去 r s， 那 我们把有 r s 的 项放在一起， 是不是就可以变成 x 减一倍的 r s 再加上三 x 的 形式？那我们来看一下这个式子要想过定点，它变过哪个点呢？既然要和 r s 无关，那只需要让 r s 前边乘的数是零是不是就可以了？因为如果它前边乘的是零的话，无论你 r s 怎么变，它是，这 这个式子是不是始终为零，对我的式子就毫无影响？所以当我的 x 减一等于零，也就是 x 等于一时， 如果我的 x 等于一，这个式子是不是就变成了 y 等于零，乘以 r s， 再加上三的形式？也是说 y 等于三，也就是说，只要我的 x 等于一， y 一定等于三，所以它必固定列，一撇三， 一撇三。所以我们这样就把我们的这三个小题全部解完。那我们来看一下整体复盘一下，整体复盘一下。 第一题，由于抛物线经过了 a 点和 b 点，所以将 a 点和 b 点带入这个抛物线，求出 a 和 b 的 值，得出抛物线的解析式。 第二题，他说直线与抛物线有且只有一个公共点， c 点，由于 c 点是他们的公共点，所以 c 点在抛物线上，所以把 c 点带入解析式，可以求出 c 点的纵坐标为一， 得出 c 点的中坐标以后， c 点呢，既在抛物线上，它也在这一条直线上，因为它是公共点，所以把 c 点带入直线，把 k 和 t 的 关系表示出来，用 k 表示出 t。 然后呢，由于此时有一个公共点，所以 有焦点嘛，就连立，与抛物线连立以后，得它等于零，解出 k 为二，得出直线 l 的 方程。那第二题的第一个小问看似很复杂，实则很简单，为什么？ 读一句写一句，将直线向下平移两个单位长度，那向下平移两个单位长度？将抛物将直线的解析式减二，得出 l 一 撇， 得出 l 一 撇以后，读第二句过点。 a 的 直线与抛物线的另一个焦点是 d， 有 焦点就连立，所以将直线与抛物线连立得出，整理以后，整理为一个一元二次方程。由于这个一元二次方程的两个解是 x， 而 x 就是 这两个焦点的横坐标， 所以利用韦达 x 一 加 x 二等于负的 a 分 之 b， 可以 得出 x a 加 x， d 等于 r 减一，求出地点的横坐标。求出地点横坐标以后，由于地点在抛物线上，所以地点横坐标为 r， 那 y 等于 r 的 平方，所以得出纵坐标为 r 平方，同理可得。 最后第三句，过这个点的直线与抛物线的另一个焦点是 e， 那 得出 e 点的坐标是 s p s 平方。继续读，当直线 m n 的 焦点 p 在 定直线上时，有焦点， 有焦点连力连力直线 m 和直线 n， 得出 p 点的坐标。虽然说计算复杂，但是实际上思路很清晰哈。得出 p 点坐标。由于 p 点在 l 撇上，所以把 p 点带入 l 一 撇，也就是 这个 y 等于二 x 减三上，得出下边这个式子。得出这个式子以后， 得出我们的 r s 等于 s 加 r 减去一个三。好，得出这个以后，它让我们去探求直线 d e 是 否过定点，那怎么办？ d 点坐标 r p r 平方， e 点坐标 s p s 平方。然后呢？把 d e 的 利用代练习数法，把 d e 的 解释表示出来，那我们表示出来它是 y 等于 s 加 r 倍的 x 减去 r s， 那 得出它以后。这里很关键， 得出了它以后，由于我们已知的是 r s 等于 s 加减三，所以我可以把它变成 s 加 r 等于 r， s 加三，那 s 加 r， 就 直接用 r s 加三来替代。那替代好以后，那这个是指它说是否过定点过定点，也就是说要与这个 r s 无关，就是无论你的 r s 取多少，它都得过这个点，所以就要让 r s 的 系数为零，所以我们把它整理为这个形式， 就是 x 减一乘以 r x 加上三 x 的 形式。现在我让 r x 的 系数为零，那 x 减一等于零，说明 x 等于一。如果 x 等于一，那 y 是 不就应该等于零乘以零加上三乘一，也就是三，所以它必过定点一撇三。 好，这是我们的这个题，那大家可以看到，我们是不是通过读题就把这道题给解了出来，也就是二三数，它其实难在计算，它不是难在啊，每个犄角旮旯的地方。嗯， 所以我不知道啊，同学们听到听完这一题以后，有没有什么感悟呢？好，然后我们再看一道题，已知 零撇负一。在二函数 y 等于 x 减 m 的 平方加 n 的 图像上，他说要求 n 关于 m 的 函数关系式还是一样的，因为这个点在二函数上，所以把这个点代入，是不是可以得出负一等于 零减 m 的 平方加上一个 n， 那 由此我就可以得出，负一等于 m 平方加 n， 那 要得出 n 关于 m 的 函数关系式，那说明 n 是 不应该等于负 m 平方减一。这是第一题，简单吧。好，再看第二题。第二题要求 m 加 n 的 最大值， 看一下 m 加上 n， 他 要求他的最大值。怎么办呢？要注意了，我的第一题要让你求函数关系式，那第二题大概率就需要用到第一题所求的东西，那所以我们选择把它变换，那 m 加上 n， n 是 不是就写成负 m 平方减一， 对吧？那此时他是不是就变成了负 m 平方加上 m 再减一的形式？那这个式子是不是可以看作一个 二函数？哎，或者说，你可以，哎，或者说你可以把它那个配方嘛，是不是就写成负的 m 平方加上 m， 然后呢？加一个四分之一， 由于前面有个符号，所以我再给他减一个四分之一，原式不变。那此时是不是就变成了负的 m 加上二分之一括起来的平方减去四分之五，那它的最大值是不是？当 m 等于负二分之一时，是不是最大？ m 加 n 的 最大值 是不是就应该等于负的四分之五？好，这是我们的第二题，那我们说男的一般都在第三题，所以我们来看一下第三题，老师把第二题擦了哈。第一题老师不知道会不会用得到他， 但是大概率需要用到，为什么？因为他可以让我们的整个式子变得更加的简单。第三题，设直线 y 等于 t 与抛物线 y 等于这么多，交于 ab 两点，那看一下，读到这画图， 画图我们这个抛物线 y 一， 很明显它的对称轴是 x 等于 m， 然后呢，大概是这样的， n 大 于零，小于零无所谓啊，因为我们只是画一个草图， y 等于 t 是 不是应该是一条水平的直线？我们假设它在这就是 y 等于 t， 因为它告诉我们 t 大 于 n， 那 因为这个点是不是应该是 m p， n 也是顶点的位置，那也是说 y 等于 t 在 他的上方，是吧？他说交于一个点是 a 点，一个点是 b 点，那我们要得出 ab 两点 以后要干嘛呢？啊？可以先把结论瞄一下他让我们求证 ab 的 长度是 c d 长度的两倍，那我们来看一下 ab 的 长度可以怎么求呢？ 那 ab 的 长度是不是就可以写成 x a 减去 x b 的 绝对值的形式，但是这样好不好求呢？嗯，不好求。那如果我能把 a x a 减去 x、 b 的 长度求出来，那同时呢，把 c、 d 的 长度求出来？也是，如果我能把 ab 的 长度求出来，和 c、 d 的 长度求出来，验证它们是不是二倍关系，那这个问题是不是就简单了？好，还是一样的老问题， 我们既然交于 ab 两点啊，什么都不管，先连立，也就是说， y 等于 x 减 m 的 平方加上 n 与抛物线， 抛物线与 y 等于 t 连立，那此时我就可以得到 x 减 m 的 平方加上一个 n 等于 t， 我们把它展开，是不是可以得出 m x 平方减去二 m x， 然后呢，加上 m 平方，加上 n 减去 t 等于零。现在它有两个焦点，一个焦点是 a 点，一个焦点是 b 点。根据尾答， x 一 加 x 二，那也就是 x a 加上 x b 是 不应该等于负的， a 分 之 b 也是二 m， 同时呢， x a 乘一个 x， b 是 不是应该等于 a 分 之 c， 也就是 m 平方加上 n 减去一个 t， 我 们先把它甩在这，因为我们现在还不知道该怎么样去使用它。再看第二个题，他说 与抛物线这个交于 c、 d 两点，那还是一样的。 y 等于 t， 与另外一个抛物线交于 c、 d 两点，那我们是不是仍然连立连立起来，不管它？ y 等于四倍的 x 减 h 的 平方加上 n 与 y 等于 t 进行一次连立。 连立以后，四倍的 x 减 h 的 平方加上 n， 就 应该要等于 t 展开，也就得到四 x 的 平方 减去八 h 倍的 x， 加上四 h 平方，加上一个 n， 减去个 t 等于零。那此时由于焦点是 c 和 d， 所以 c、 d 两点的横坐标 x c 加上 x d 就 应该等于负的 a 分 之 b 是 不是就应该等于二倍的 h， 而 x c 乘以个 x d 是 不是就应该等于四分之四 h 的 平方加上一个 n， 再减去个 t？ 好， 得出这个以后，我们把这些擦了。 这个画图只是便于我们理解，他要让我们去证明 ab 等于二倍的 cd， 但是 ab 有 多长我不清楚，因为我的 ab 是 不应该等于的是 x a 减去 x b 的 绝对值，而我的 cd 是 不是应该等于 x c 减去 x d 的 绝对值？因为我不知道 c 和 d 哪个在左边，哪个是在右边，谁大谁小我不清楚，那我直接去求他们，是不是要需要讨论非常多啊？ 由于 a、 b 是 线段，它一定是一个正数， c d 也是线段，它必然也是一个正数，那正数嘛，我就给它平方，要让我证明 a、 b 等于二倍的 c、 d， 也就是要让我证明 a、 b 的 平方是不是等于四倍 c、 d 的 平方，我证明这个就行了，所以我把它平方一下。 所以我是不是可以得到 ab 的 平方就应该等于 x a 减去 x b 的 平方，那 x a 减去 x b 的 平方，我要求它，但是我知道的只有 x a 加 x b 和 x a 乘以 x b， 那 此事怎么办呢？ 好，那我们可以看一下我们以前学的 a 加 b 的 平方等于 a 平方，加上二 a b 再加上 b 平方，而 a 减 b 的 平方是不等于 a 平方，减去二 a b， 然后呢，再加上一个 b 平方，那很明显，我们可以看出来的是， a 加 b 的 平方 减去 a 减 b 的 平方是不是恰好等于四 a b？ 也就是说 a 减 b 的 平方是不是就应该等于 a 加 b 的 平方减去一个四 a b？ 那 由这个信息我们是不是就知道 x a 减 x b 的 平方是不是就写成 x a 加上 x b 的 平方，减去一个四倍的 x a x b， 对吧？那 x a 加 x b， 我 们已知 x a 乘以 x b， 我 们也表示了出来，那我们是不是可以把它整理出来了？那我们整理一下， x a 加 x b， 用二 m 来替代，也就是四 m 的 平方，减去四倍的 x a 乘以 x b， 也是四倍的 m 平方，加上一个 n， 再减去一个 t， 那 它就等于什么呢？它是不是就等于四 t 减四 n？ 所以 这是第一个式子，老师把这边擦掉哈。 然后这样 ab 平方就已经表示了出来。而我的 c d 平方是不是就应该等于 x c 减去 x d 的 平方？用同样的方法，它是不是可以写成 x c 加上 x d 的 平方，减去四倍的 x c， 再乘以 x d， 而 x c 加 x d 是 不是等于二 h， 所以 它等于四 h 的 平方，减去四倍的 x c 乘以 x d， 而 x c 乘以 x d 等于这么多，那也是减去四 h 的 平方，减去 n， 再加上一个 t， 所以它等于 t 减去一个 n， 那 ab 的 平方等于四 t 减四 n， 而 cd 的 平方等于 t 减 n。 而且题上告诉了我们， t 大 圆说明它是一个正数，那我们是不是就可以知道 ab 的 平方应该等于四倍 cd 的 平方， 对吧？ ab 平方等于四倍 cd 平方，由于它是线段，所以 ab 一定等于二倍的 cd， 是 不就可以得正？那看一下我们是不是在读题的过程中就把这道题给解了出来，那当然以后去遇到还有那种什么啊， 与相似相关的，与圆相关的，其实也大差不差。那那个过程中可能就填几条平行线或者垂直于 y 轴的垂线啊，就可以把它解出来。那我们下一个视频再讲与几何，也就是与相似相关的一些题型。 那我们常说，要想数学考得好，点赞关注少不了，赶紧关注助理老师，我们下期视频再见。

一起来看一下今年一减十六题填空压轴题。这一题对于填空压轴来说难度不算大，基本上平时有练的同学做起来是比较顺的。 而且这类题型有很显著的特征，就是求线段最值，并且我们发现它可以构建线段之间的关系，所以我们可以用代数的方法来解决几何当中的最值啊。那我们先看一下题目， 题目给的条件是，这一段 a b 长度等于二， c 段长度用 m 来表示， m 多少不知道，然后 b c 的 长度是二，给了三个垂直，那么这三个垂直是我们经常见到的图形。一条线上三个直角， 那也就是一线三等角，我们可以用相似。那先看一下他问的问题， m 最小值， m 的 最小值就是 c 档的最小值，要求的是 pe 与 c 档的交点，我们把它定义为这个 h， 要求 h 一定要在 c 档上，那大家可以思考， 如果 c 弹太短了，那 h 就 跑到 c 弹的外面去。所以我们看似研究 m 最小值，实际上要先研究一下 c h 的 长。 当我们知道 c h 的 范围，那么很容易就知道 c 弹的范围了。好，那可能一眼无法看出思路。我们先来研究一下这里面的相似，把已知条件变成更多的已知条件。 因为这段长度为二，所以我们为了列相似，需要把这两段表示出来， c p 跟 b p， 所以 我们可以设其中一段为 x， 另一段就是二减 x 啊。异正，这两个三角形相似啊，很好，正 角一加角二九十，角二加角三九十，所以这个角一就等于角三了。接下来相似以后，我们依次写出它们对应边的比例， ab 比去这个 c p 等于 b p 比去 c h 啊，好，那依次把线段带进去就行了。 ab 是 二 p， c 我 们设为 x， 那 么 b p 二减 x， c h 保留，因为我们研究的是 c h 交叉相乘， c h 就 等于这个，那么这个大家发现它是个二次函数，二次函数，而且开口是向下的哈，这个负开口向下呢？待会有个最大值，那我们先看一下它最大值哈，先把它展开，展开以后配成顶点式。 好，那这个二叉数开口向下最大值是二分之一，这个顶点重坐标二分之一。二分之一代表的是 c h 的 长度，最大大到二分之一。 既然 c h 最大大到二分之一，那么如何保证 h 一定在 c 档上呢？ 只要保证 c 大， 不要比二分之一短就行了。所以 c 大 大于等于二分之一，也就是 m 要大于等于二分之一， 那最终 m 的 最小值就是二分之一哈，那最后总结一下这种类型的题啊，首先求最值，最大值或者最小值哈，并且呢，它可以在几何当中构建关系。最后我们通过 代数的问题求线段的最值，那这种类型的题，如果没练过的同学可以集中练五道六道题，你就一定会有心得体会。

好，我们来看福州一剪的第十六题，那 ab 平行 c 档角， b 是 九十度， ab 等于二， bc 等于二， c 档等于 mp 为一个动点，将 pa 老 p 点旋转，逆顺时针旋转九十度。好，那我们可以得到 ape 是 九十度。 好，那这里有很明显有一个东西啊，一个垂直，两个垂直，这里是不是也是垂直？三个垂直，那这里是不是就可以转化成我们的一线 三垂直的模型，对吧？那这里，哈，这里，这个，我们给他一个焦点，给他点 f。 好， 那这时候是不是一线三垂直的相似模型啊？ 相似，也就是这里的三角形 p， c、 f 是 相似于这里的 a、 b p 的， 对吧？这两个三角形是相似的。 好，他这里当时他问的什么？他问的是这两个穴位，他这两个线段 p、 e 跟 c 档他总有交点，并且这个交点总在 c 档上面。问这个 m 的 最小值，也就是 c 档的最小值，他问的是 c 档的最小值。 好，那在这个图上里头，也就说明啊，他这里说明他的焦点，他总在这个 c 档上面，说明什么呢？说明我们这个 f 点一定要在 c 档上面， 对吧？那 f 点一定要在 c 档上面，那我是不是求 c 档最小值，我就转化成什么了？ c f 的 最大值。 好， c f 的 最大值，如果 c f 的 最大值都在 c 档上面啊，它刚好就等于 c 档， 那说明啊，不管 cf 再接下来再怎么变化，它一定一定都会在这个线段上，都会在 c 档上，所以我们把 c 档的最小值转化成什么？ cf 的 最大值？问题， 好，可以吧？好，那放到这里来说，也就是什么呢？好，我们可以应用通过我们的干海的相似，我们可以得到 cf， cf 比上比上我们的 b p， 对吧？等于我的 c p 比上我的 ab， 好， 我们这时候带数字进来， c f 就是 c f 吧？ 那好， b p b p， 我 们这里没有其他的数字，那我们可能设个参数，比如说 c p 是 为 x， 那 这条边是不是就二减 x？ 好， 那是不是 c f 比上二减 x 等于 x 比上二？ 好，我们整理一下，是不？填到 c f， 它是等于负的二分之一， x 平方加 x。 好， 那这个东西长得像什么？是不是很像我们的函数？ 那求这个函数的最大值，是不是我们接下来可以通过顶点啊？求这个函数的顶点就可以知道。那我们就可以进行一个配方嘛，对吧？那我们配完方负的二分之一提出来，它可以整理成 x 减一的平方加二分之一， 对吧？那是不是就可以知道当 x 等于一的时候， x 等于一时，这个 c f 就 会有什么最大值？哈？ c f max 就 等于二分之一， 对吧？好，刚才说了， c f 的 最大值就是 c 大 的最小值，所以这一题它 m 的 最小值就是什么？就是二分之一。好，这就是第十六题。

好，我们来看一下福州这次一减数学的第十题，若二次函数 y 等于 a， x 平方加 c， 它的图像经过四个象限，问，下列判断一定正确的是哪一个？好， 那看这是二次函数，考察的是二次函数的图像的性质问题，所以我们需要去画草图。哈，那画草图的话，那开口向上向下是不知道的， 所以我们是不是要进行一个分类讨论，如果开口向上， a 大 于零的情况下，那我们画一个草图出来，比如说他要经过四个象限，既然要经过四个象限，他的顶点，我们先确定顶点吧。顶点是不是一定要在 x 轴的下方？如果在 x 轴上方的话，是不是就这么画了？ 因为开口向上吗？是往上延伸，那这样下面两个象限我是不会经过的，所以不可能往上划。好，如果往下划呢？我们比如说 x 啊，顶，它的顶点在第三象限。好，第三象限我是不是可以这么划， 但这样的话是不是就会经过四个象限？好，如果再画，我再换一种画法啊？如果是这样画， 这样的话，是不是我的第二种画法是不是没有经过第四象限，对吧？那是不是这种情况就不存在？ 不可以是这种情况，对吧？但这两种情况区别在什么地方呢？好，它的区别就在于我与 y 轴的这个交点，一个是在外的正半轴，一个是在外的 负半轴的话，是不是说明我的 c 是 小于零的？ c 是 小于零的， 对吧？好，那有可能有没有其他的画法，比如说我开口不在这边的话，我开口我开。哦，我的顶点不在这边，我的顶点不在这边，我换一个吧，我顶点在第四象限，第四象限我是不是也是这样？这样画，这样是不是得会经过四个象限， 对吧？那这种情况下，我的 c 是 不是一样在复盘中，对吧？ c 一 样是小于零。 好了，如果说啊，我们换一种情况讨论 a 小 于零的情况下，好， a 小 于情况下，我们一样画出超图吧。 那根据刚才推理哈，如果要经过四个象限，这时候开口要向下了，所以这时候的顶点要绑在第一象限，要绑在第二象限，因为他要往下延伸，如果在第三根第四象限再往下，是没有交点的，对吧？好， 那在第一或者第二象限，我们就可以画草图，比如说我在第二象限，我就画一个草图， 哎，我这样画是不是会经过四个象限，对吧？好，那我换一种画法哈，我换一种，我这么画啊，这个可能太长了，我画过来一点，这么画，画小一点，对吧？画小一点，我同样，我开口向下，但是这时候啊，他是不是没有经过第一象限啊？ 那同样的，这两个函数的区别在啥？不，不管说大小也好哈，它区别在于什么呢？区别就在于这两个与 y 轴的交点是不是一样的，一个在正的，一个在负的， 对吧？那经过四个象限的这一根，好，我把这根擦掉。经过四根象限的这一个函数，它的 a 是 小于零， a 是 小于零的，但它的 c 在 正半轴是不是大于零， 所以两个合在一起， a， c 是 小于零，可以确定。那跟 b 为什么会没有关系呢？因为我发现我要不然在第二项线画图，或不然我在第一项线画图， 那我们根据 b 跟 a 的 关系是不是 b 与 a 的 关系是不是叫左同右异， 对吧？那说明什么呢？我 a 在 确定大于零的时候或者小于零的时候， b 它干嘛？ t b 它不确定， b 是 不确定的，所以这里 a b 的 乘积是不能固定的，因为 b 不 确定。好，所以这一题我们选的是 c 选项， a， c 小 于零。

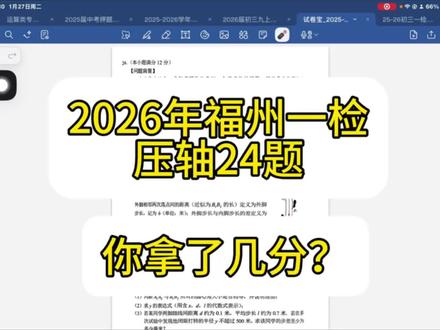
好的，各位同学，各位家长来，今天所讲的就是我们福州市医检的第二十四题，怎么样？现在全网还没有老师开始讲这道题，是不是？哈哈，这会已经是深夜了啊，今天下午苏老师开了两场直播，下午开了一场，晚上开了一场， 也都把这个二十四题已经讲过了，但还有很多同学没听明白，那么还有老师很多同学没听到，苏老师再给大家详细的讲一遍，这个东西叫什么呢？叫做综合数据分析题啊，我们叫综合 分析题，那么这种题呢，其实是属于定义新运算的高级版本啊，他是属于定义新运算的高级版本，他把一种定义类的游戏规则与几何图形圆的知识结合到一起。 那么这道题呢，很多同学都已经看的大脑发热，是不是啊？可能这会啊，大家可能没有什么时间，没事大家先点个赞啊，点个关注，或者是转发起来，收藏起来，回头慢慢再看。那这道题的核心呢？是什么呢？是一定要搞明白这里面的运算规则， 而这个里边的运算规则有多少种呢？我们来详细的看一下。对于这个题来说，首先这个位置如果你没有详细的拆解明白，所以这道题你是做不出来，那么我们在拆解的过程当中一定要注意啊。来第一步， 这是一个同心圆儿，圆心为 o， 所以 第一步你要先明白，它有一个半径 o a， 有 一个半径 o b， 还有个半径 o c， 那 么分别以 o a、 o b 为半径的时候呢？这个时候我们有一个叫做 c a 等于 c b， 什么叫 c a 等于 c b 呢？来这个位置是 c， 这是 c a， 这是 c b， 也就是这两段距离完全是相等的。这是这道题第一个算式，你要先整明白，然后紧接着呢，这里面的内角和外角踏外线， 这个时候内外线之间的距离，哎，这段距离 ab 之间的距离是大， 那也就是说 o b 减去 o a 啊，就等于这个，当这是第二个关系式，我们一定要也弄明白的。 紧接着第三个关系式，就是这个 o c 等于 y。 这道题是隐藏的比较深的啊，这个 o c 等于 y， 那它与 o a 和 o b 是 什么关系呢？来，我们来看一下。说 y 等于 o c 啊，那它等于 a， 哎，我设这个 o a 为小 a 哦，这是小 a 的， 这两边是小 b， 那 么我就明白了哦，如果我把 o a 加 o b， 那 等于什么呢？等于小 a 加小 a 加二 b。 好， 如果我把 o a 加 o b 除以二，它除以二，是不是刚好就是 a 加 b， 所以其实我们的 o c 就是 二分之 o a 加 o b。 所以 在写的第二、第三个关系式里面呢，我们就明白， y 等于 o c 等于二分之 o a 加 o b， 这个事非常重要。 好，紧接着再往下读，这里边的 a 一 和 a 二的长度为内角长，也就是往前迈一步， a 一 a 二之间的距离是 a， 那么 b 一 b 二的距离是 b， 是 不是这个意思？所以左脚迈一次 a 一 a 二等于 a， 右脚迈一次啊，右脚在这呢，右脚迈一次 b 一 b 二等于 b 啊，你看，我写了第一个关系式、第二个关系式、第三个关系式、第四个关系式、第五个关系式， 那这里面又出了第六个关系式，就是这个 x， x 是 什么呢？是 b 这一段距离和 a 这一段距离的微小的这么一个叉， 也正是因为这么一个叉，最后才会实现这么一个顺时针的走走圆，知道吧？哎，就是外角的这个 b 啊，外面的角这个 b 和比里边这个角啊，走的距离要稍微长，那么 x， 所以 这 x 等于 b 减 a， 也是非常重要的一个关系式啊。我们再看 最后这一段话，是很难理解的，他没有关系，你就是理解不了，你也可以明白，这两段之间的差距叫平均不长，哎，叫平均不长，平均不长是什么呢？他就是四分之 a 加 b。 所以这道题的第一步，你一定是要先把这个读明白，读完明白之后，你能有这样的一二三四五这五个关系式，你才有可能做出来第一步。 但很多同学啊，在在啊，可能做着第二步，很多同学在第一步就卡死了，那第一步怎么卡死的呢？那是因为他们没有看明白，这本身还是一个圆的问题， 它本质上就是一个圆的问题嘛。他问说这个啊， b 一 b 二和 a 一 a 二弧所对的圆心角度数是不是？那么你很简单嘛，你把 o e a o 啊 o a 二 o b 一 和 o b 二，你把它连上， 那这本质上这一段距离和这一段距离也是相等的，所以你看他是不是有一个手拉手的旋转全等， ok， 这个旋转全等之后，就意味着他俩全等，全等完了之后，我们是不是就有角一等于角二了？那么一加三不就等于二加三， 对不对？所以 a 一 a 二弧与 b 一 b 二弧所对的圆心角就是相等的， 那也由于这个第一步你能看出来，你再把这俩连上，你把 a 一 a 二连上， b 一 b 二连上，那这个图形与这个图形不就相似了吗？ 一旦它相似，那我的 a、 b、 b 来注意，一旦相似，我的 a、 b b 是 不是就是 o a b o b？ 所以这也是第二问，刚才我说的五个关系式中最隐藏的一个，如果你这个没有发现，那你是完全做不了的。好，第一问结束了，啊，啊，圆形角相等，那我们来看第二问。 第二问，我们通过这个东西的分析，找到了一二三四五这么五个位置关系，这五个位置关系生成之后，我需要对一二三四五这五个关系式进行一个详细的运算， 那这个运算呢？苏老师再给大家算一遍啊，大家认真听，这个计算过程可是相当的复杂，那也是大概率考的我们的代数推理。首先看我们的第一个关系式，我们先找一个 ob， o b 等于什么呢？ a o b 等于 a 分 之 b 倍的 o a。 好， 再结合第二个关系式，我把 o b 换掉， o b 换掉，这不就变成了二分之 o a 加上 a 分 之 b 倍的 o a。 好， 我提取 o a 就变成了二分之 a 分 之 a 加 b 括号，那么就等于 o a 倍的二 a 分 之 a 加 b。 哎，这个看懂没有？那这就是我们的什么哎，我们的第二步的过程，在第三步的过程当中，我们发现这个算数还没有用的，但等于 o b 减 o a。 好的，那么此时我就可以知道哦， o b 是 什么呢啊？ o b 是 等于蛋加 o a， o o b 等于蛋加 o a， 那 这个再换过来，我把 o b， o b 不 就换掉了吗？ 对吧？所以它就变成了什么叫做 a 分 之 b 倍的 o a 等于蛋加 o a， 那 我们的蛋 这个蛋就等于 a 分 之 b 倍的 o a 减 o a。 好 的，那蛋就等于 o a 倍的 a 分 之 b 减 a。 通过这个运算，我找到了 o a 等于蛋乘 a 除以 b 减 a。 好 的，这个 o a 我 找到了，我发现这个位置我往回一荡，我就可以换掉 o a， 因此最后我就得到了这么一个算式，叫做 b 减 a 分 之蛋乘以 a， 再乘以二 a 分 之 a 加 b。 那么在这个运算过程当中呢，你得运气很好，一下子算对 a， a 约掉，最后变成二乘以 b 减 a 分 之三倍的 a 加 b。 好的，最后我们终于到了第四步，我发现这两个东西我还没有用呢，是不是？所以我们的 a 加 b 是 等于四 l 的， 我的 b 减 a 是 等于 x 的， 好的，我把它进行一步的替换， 最后就变成二倍的 x 分 之四 l 倍的 d， 那 我们把二二预约，这就变成 x 分 之二 l d， 因此这就是第二问。所以这个第二问的要求和难度是比较大一些的，对不对？哎？但前提是你必须把这幅图里面的这些位置关系和数量关系都给他挖出来，才能导出这五个关系式， 明白了吗？好的，我们再看第三问，这个第三问呢，其实基本上是在第二问的基础之上，你已经找到了 y 等于二倍的 dl， 其实这是不是一个反比例函数呢？ 对不对？如果你直接计算，那就是二乘以零点七，再乘以零点一，最后 x 分 之零点一四， 但这个东西呢，我没有那么做啊，我也是这么代入的，直接代入不等式，在这个不等式里边呢，最后有一个 x 大 于等于五万分之十四米，可是题目要的是毫米啊，那么我们干脆就把它换成毫米，怎么说？乘以一千， 消掉三个零，变成五十分之十四，所以最后 x 是 大于等于二十五分之七，等于零点二八毫米。所以同学们，你做对了吗？怎么样？哈哈，这次的二十四题是不是非常的炸裂，他几乎是参考了， 他参考了我们二零二五年中考的二十四题，所以这种综合实践分析题对大家要求还是比较高的哈。同学们继续努力啊，明天继续加油一姐，考个好成绩，苏老师等你好消息。

同学们大家下午好，今天大家讲一下十六题，他说如图啊，在我们四边形 a、 b、 c、 d 当中， 然后呢， a、 b 是 平行于 c、 d 的， 对不对？那么角 b 等于九十度，我肯定知道这个角 c 这里也等于九十度，对吧？两支平行同旁的有互补嘛，对不对？ ab 等于二，好吧， bc 也等于二，那么说我们 c、 d 啊，它的长度 m， 那 么 p， 为什么呢？ bc 上一个动点，对吧？ p 为我们这个 b、 c 上一个动点，连接我们的 pa， p 将 pa 这个顺时针给它九十度，得到 pe， 所以 说这个角为九十度，好吧，哎，这里为九十度，这里为九十度，这里也为九十度。大家想起什么？想起我们考前讲的是不是叫做一线三角模型啊？对不对？是吧？这个题目我们太熟悉了，肯定是遇到过类似的， 叫做一线三角模型，对不对？那么不就是正三角形和这三角形相似吗？对不对？是吧？那你看好我们这题目是不是这样做的。他说，若点 p 啊，在线段 b、 c 上有点 b 向选 c， 点 c 运动， p， e 与 cd 的 交点在线段 cd 上，对吧？则 m 的 最小值，那么求 m 的 最小值，这个 cd 为 m， 对 不对？是吧？ 好的，那么我想我，我刚说了，我们这个一三角模型是正三角形和三角形相似，对吧？那么我假设这里一个交点于谁呢？我假设 a， b， c， d， e， 我 找这个点 y、 f， 好 吧，行吗？好吧， ok， 这时候我看一下，你看角一加角二是不是等于九十度，对不对？是吧？这个也等于角也等于九十度，所以说角二加角三也等于九十度， 旁边这个角角角二加角三也等于九十度，那么你看角一加角二等于九十度， 我们的角二加角三也等于九十度，所以说角一是不是应该等于角三啊？没问题吧？角一等于角三，这里有个九十度，所以说这两三也相似啊，对不对？是吧？哪两三也相似写出来，所以说三角形啊， a b p 相似于三角形，从点 p 出发， p c f， 对 不对？是吧？ ok， 那 么这时候我们把它相似比写出来，是不是有一个 a b 比上我们的 p c， 对 不对？等于 c 等于 b p 比上一个 c f， 好 吧，那么我设这个 b p 为 x， 可以 吗？好吧，那我的 p c 是 不是二减 x 啊？没问题吧？因为这个 b c 等于二嘛？ ok， 这时候 b p 我 有了， p c 我 有了， ab 我 也有，等于二，对不对？把它带进去嘛，对吧？ ok， 那 么这时候 ab 等于二比上这个 p c p c 等于什么呢？二减 x， 好 吧， 等于我们的 b p b p 等 x 比上我们的 c f， 对 吧？ c f 这时候交叉相乘相等两倍的这个 c f 是 等于 x 被括号二减 x， 对 吧？等，所以说 c f 就 等于什么呢？二分之 x 被括号二减 x 等于负二分之一 x 的 平方，对吧？加上个二 x， 是 不是再加上一个 x 啊？对不对？是吧？ ok， 这是一个二次函数，对不对？ 是吧？那么我们想求 m 这个最小值，是不是？实际上求什么？不求我们的 c f 最大值吗？对不对？ ok， 我 的二次函数开口向下有最大值吧？ ok， 把负二分之一提出来，对，负二分之一被夸 x 平方，对吧？减去个二 x， 对 不对？加一个一， 一，再减去个一，好吧，等于负二分之一，被括号 x 减一括号的平方可以吗？好吧。再加上一个二分之一，那么当 x 等于一的时候，对吧？当 x 等于一的时候，这个 c f max 等于多少？等于二分之一，对不对？是吧？ c f 等于二分之一，那么不就是我这个 m 啊，等于多少？我的这个 m 不 就也应该等于这个二分之一吗？好吧，结束。

最近很多初三同学问我，福州医检数学到底考什么？难不难？今天我就用几分钟的时间给大家讲清楚。首先，医检是什么呢？他是初三上学期的期末考试，主要检测九年级上学期的学习成， 考察范围呢，是从九年级上册的一元二次方程到九下的相似这一块。那整体难度怎么样呢？实话实说，一减一般比后面的二减和中考要更难一些，因为它不仅考九年级的知识，还会涉及中考常见的压轴题型，比如说二次函数、 旋转圆相似、四边形综合那一些。那么基础题应该如何准备？历年一减的基础题型其实是比较稳定的， 建议各位把前三年的卷子刷一遍，这样就能够摸清楚每一章节的基础题怎么考。不过要留意，现在的基础题也喜欢跨学科出题，尤其是和物理结合， 平时可以多注意这类题中难题有什么样的趋势。最后几道题，比如说二十二到二十五题，会紧跟近几年中考的导向， 重阅读、重创新、重思维。去年一检就新增了材料阅读理解。根据去年中考的情况，今年除了继续关注圆综合、四边形综合这些经典题型之外，建议大家多练练方程、 函数、代数、推理和阅读量较大的题目，这类题型正在变多。一检是一个很重要的阶段性检测，既考基础，也考能力，大家一定要稳住节奏，扎实复习，一定没问题。

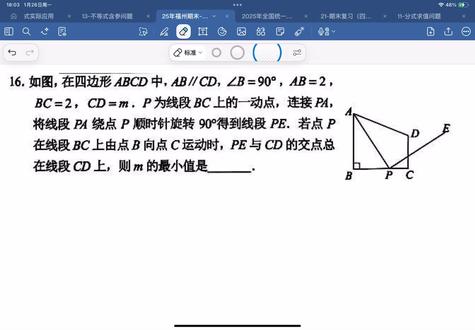
呃，各位同学下午好，那继续往下，翔哥来带大家看一下第十六题，题目给到我们一个四边形 a、 b、 c、 d， 已知条件说 a、 b 平行 c， d， a， b 平行 c， d 的 潜台词就是角 c， 这是一个直角。 那么继续往下，题目给了我们一些线段长度，我们把它标注到图中， a、 b 等于二， bc 等于二， c 段的长度是 m， 那 从而我们可以看出这个 m 它不是一个定点。 题目说 p 是 下方 bc 的 一个动点，在这个 bc 上从 b 往 c 运动，那 bc 就是 它的两端两个运动边界，然后沿顺时针方向旋转九十度，将这个 a p 旋转到了 pe， 那说明这个 ape 它是一个等腰直角三角形，那么说明稍后有可能要利用到这个等腰直角三角形来构造 k 型全等啊，因为它的这个构图很像是一个一线三等角啊，少了一个直角的构图有可能，但不一定。那么再往下，它要我们求什么呢？要我们求如果 pe 与 c 档， pe 在 这， c 档在这，他们的焦点在这个位置，我们把这个焦点取一个名字叫 f 点，也就是说这个 f 点的位置。他说如果总在线段 c 档上，在线段 c 档上的意思就是在 c 点跟蛋点中间的意思，要我们求 这个线段啊， m 的 最小值就是线段 c 档长度的最小值。那么大家来想一件事情，我现在把这个 f 跟蛋的位置来做一个对比，大家看，你这个 f 如果要永远落在 c 档当中，它其实本质上就是要干嘛呢？ 本质上就是要对比 c、 f 跟 c 弹这两条线段的长度。我们假设 c 弹的长度是二， c， f 的 长度是一，那一比二短，这个时候 f 肯定被夹在 c 跟弹的中间， 假如说这个 c f 的 长度啊等于二， c 弹的长度，那等于一个一点九，那么这个反过来的话，就会我们就会发现 f 就 跑到外面去了，这就不行了， 那相比通过这个对比，大家就看懂了，其实他的等价条件就是要满足什么呢？就是要满足 c 档的长度大于 cf 的 长度。假设这两点刚好重合，那应该也是符合题的，所以 c 档要大于等于 cf。 所以 这道题目真正的问题就是要我们求出 c 档大于等于 cf 时，他的一个 最小值，那大家说要求 c 档的最小值，我们是不是就可以先转为去分析 cf 的 长度？那么回到这个图中，怎么研究这个 cf 的 长度呢？通过观察我们可以发现这是个直角，这是个直角，这是一个直角，这天然存在的一组一线三等角的结构，所以在三角形 abp 和三角形 p c f 之中，这本身就存在着一种天然的什么呢？一线三等角所带来的 k 形相似，下一步我就可以利用什么呢？就可以利用对应边乘比例来表示出 c f 的 长度。好，现在这个 ab 的 长度是二， 那我把对应边标成相同的颜色，它的这个对应边 p c 的 长度位置，那我可以先把 b p 的 长度设为 a， 那 么这个 p c 的 长度我就可以设成什么呢？这个 p c 的 长度，我就可以把它表示成二减 a， 因为整段是二，拿走了 a， 剩下二减 a， 而我们要求的这个 c f 的 长度不确定，我就先把它设成 b， 那 么利用对应边乘比例，蓝边比蓝边等于红边比红边，我们先写它的这一个那名字， cf 的 对应边啊，应该是 b p 啊， cf 对 b p 好， 这个 k 型相似的对应边叫啊右对左下，左对右下啊，两组对应边，那么另外一组对应边就是一个 pc 比 ab 等于 pc 比 ab 好， 然后我们把它列出来，就是一个 b 比去啊，比去 a 等于一个 pc， 就是 二减 a 啊，比 ab 就是 比一个二 好。然后我们把这个分母 a 乘到等式的右边去，我们就可以得到 b， 可以 写作是啊，把这个分数我们给它分离陈述一下，就是一减去二分之 a， 再乘一个 a， 再把括号去掉，就是一个负二分之一 a 方啊，再加上一个 a， 如果我们对它配个方，它就可以变成一个负二分之一倍的 a， 减去一的完全平方，括号外面应该是加上一个二分之一。这个计算过程难度不大啊，我这边就不展开说那么细了。 那么接下来我们去分析一下他这个四变量 a 的 取值范围，因为 b p 他 是落在 bc 上的一段，这整条线段长度是二，这个说明 a 的 长度肯定小于二，哪怕重合的话就是等于二，那么从这个地方出发，他的最小值应该是零，所以四变量 a 的 取值范围应该是落在零到啊二之间。 那么说明什么呢？说明它是可以取得对称轴的，对称轴是 a 等于一，因此当 a 等于一时，因为这条抛物线开口向下，那这个函数就有最大值， 这个最大值就是 b 的 最大值啊，它的最大值就是一个二分之一，那么这个最大值就是谁呢？就是这个 c f 长度的最大值，所以 c f 长度的最大值就是一个二分之一， 那它的最大值是二分之一，说明什么呢？我们把这个 bc 这条直线所在直线想象成地面，这就说明 f 点离地面的一个最远距离是二分之一。如果你这段长度永远要被 c 弹包在内的话，那就说明这个 c 弹的长度至少也要比二分之一大一点点， 最少最少也得是跟这个二分之一重合的情况。那么从我们就可以从中看出， c 大 的长度要大于等于二分之一，那说明它的最小值就是谁就是二分之一。所以这道题目最终的答案就是啊，二分之一。

讲一下最新的五中稀缺的这个期末考试的第十题啊，我们来看一下题目。首先审题， c 呢等于 c， b 等于二。标一下二二角 a， c、 b 呢等于九十度，所以这样能得到一个等腰直角三角形 a、 c、 b， 因此 a、 b 呢等于二倍。根号二 点 d 呢，在 b、 c 上运动， d 是 动点 d。 在 运动的过程中呢，以 a、 d 为边，做一个正方形， 做一个正方形，过点 f， 再做 f， g 呢，垂直于 c 的 延长线，交它呢于点 g， 然后把 f、 b 呢给它连起来啊，交这个 d， e 呢于点 m， 这个 d， e 呢又跟这个 a、 b 呢交于点 n。 问，下列说法错误的是， 那这一题很显然它是一个怎么样反照这个二五年咱们的这个中考题出的一道这个压轴，对吧？我们这二五年的那个背景的话是一个刮豆模型，那这题依然还是一个呃，刮豆模型。所以这一题的话，就需要大家对刮豆模型呢有一个非常熟练的一个了解。 好，我们来看一下啊，这个刮动模型呢，我们就先不在这里面介绍了，有兴趣的同学。嗯，可以看我以前录的这个视频。我们来看一下这个刮动模型的话。呃，很显然这个点 d 呢是主动点， 点 e 呢是从动点好光度模型满足什么呢？就是主动点到定点的距离跟从动点到定点的距离比是一个定值。那这题很显然， a、 e 比上 a、 d， 就 这有个距离比， 这个距离比很显然等于根号二是一个定值。还有一个就是夹角的这个夹角，比如说主动点 和定点的连线，从动点和定点的连线，你看，以定点为顶点组成的这样的一个夹角，那这个夹角呢？也得是一个定角，那这题很显然它是一个四十五度，有了这两个条件，它才符合我们的这个刮动模型。 那刮动模型的话，熟悉的同学应该知道，就是主动点的轨迹它是一致的。现在主动点的轨迹呢， 是在一条直线啊，或者说他这是直线上面的一条线段，那么我点 e 呢？他应该也是直线上的一条线段，对吧？那么所以这样的话，我们就可以把从动点的轨迹给他，干嘛给他确定，我们要确定这个从动点的轨迹， 那从动点的轨迹呢？如何去确定呢？方法呢？有很多。那这题比较特殊，我们可以通过主动点的特殊位置去找从动点的特殊位置。 大家来看一下 d 点在特殊的位置时候，能推 e 点的这个特殊的位置，我们就把 d 放在哪个特殊位置，你比如说 d 可以 在 这个 c 的 时候，对吧？那如果 d 跟 c 重合，此时 a d 是， 是这个对不对？那很显然，那我的这个 d e 呢？是不是就呃等于这个 c b， 所以 这个当地在 c 的 时候，那 e 呢？是不是在这个地方？这帮我可以标个 e， 对 吧？好，那这时候我们再找 d 的 一个特殊位置， 那显然我们可以找当 d 在 b 点的时候，你是不是以 a d 为边？是不是再向外面再做一个？等腰直角三角形的时候，或者在外面再做一个这个，呃，正方形的时候，给它擦一下，那此时这个正方形画出来了，那刚好 应该是长这个样子啊，那刚好应该是长这个样子啊，那差不多呢，嗯， 在这啊，这个地方我图就不要画的特别准了啊，那很显然，那这是一几啊？这是一二，你看这三个点刚好在一条线上面，一一一二一三，我们刚才知道这个从动点的轨迹是一条直线，对吧？其实我只要找这条直线上面的两个特殊的点，就能把这条直线给它，缺什么给它基本确定了啊。 好，那这样的话，我们的一点的轨迹呢，就全部怎么样解决了？把这个图给它擦掉，五官的图都给它擦掉啊， 那这个一二的这个点的坐标呢，也比较特殊，也比较特殊，那我们来看一下啊，因为这个角是四十五度，这个角呢也是这个，呃，四十五度，所以这个三角形，这个三角形相当于就是一个等腰直角，是吗？三角形啊， ok， 那 我们现在把这条线呢再给它延长一点点，那整个 e 呢？就在这条直线上面干嘛动啊？这上面动。 好，嗯，我们来看一下啊， a 选项，他是说了当这个点 d 在 直线 bc 上面运动的时候，也就是说 a 选项有一个关键词，他把地点的这个运动的一个范围，从刚开始的这个边上面运动扩展到了这个直线上面运动， 所以现在这个 e 点的轨迹也是在整个直线上面动，而 a 选项让我们求 a e 加 c e 的 最小值，那很显然 a 选项求的是 a e 加上 c e， a e 加上 c e 的 话，它的一个是线段之和的最什么值？最小值，因此的话，那 a 选项很显然是一个将军印什么印码，而且是两定一动， 你看啊， a e 加上 c e 的 这个最小值，那很想我是不是做一下对称就可以了啊？那我就把 c 点关于它对称一下，我们把图给它标一下。 好，咱们把这个 c 呢给它对称过来，用个绿色的吧，对称过来，好，对称到这个地方，这边标一个 c e 撇， 那此时的话，我们的这个 c e 是 不是就变成了 c 撇 e， 然后直接连上 a c e 撇是不就可以了？也就是说，此时 a e 加上 c e 的 最小值，是不就等于 a c e 撇， a e 加上 c e 的 最小值，等于 a c e 撇，我们怎么去计算？那很显然我们还是要去。呃，添加辅助线，把它构造成一个直角三角形，我可以过 c 呢，往这边再做一条垂线啊， 这方我标个点 m 点 q 吧。 ok， 那 么现在我们开始一个计算，呃，咱们知道这个角呢，可能说是四十五度，那这个角呢，也是四十五度，所以 三角形这个地方呢，这个三角形它是一个等腰直角三角形，这条边呢是二，因此的话，那这个，呃，这条边的长度呢，就等于根号二。对称过来，这个长度也是根号二，这个方是垂直的，所以我们的 c c 一 撇呢，等于二倍根号二，是不等于二倍根号二， 而这个角呢等于四十五度，这个角呢也等于四十五度，所以我们的 c 一 撇 q， c 呢，它是一个等腰直角三角形，因此这条边呢， c 一 撇 q 等于二， c q 呢也等于二，所以我们再用勾股定顶，就能把它长度呢给它算出来了啊。那此时很简单，等于根号下， 应该是二的平方，再加上四的平方，所以答案呢，应该等于二倍杠五，所以这题的最小值呢，应该等于二倍杠五，并不是等于二倍根号二加二。如果你选了这个答案，你是估计没有看到这个关键词，它是在直线上面运动。好，这是 a 选项，所以当然呢，这题呢，就直接选 a 就 可以了。 这个和我们二五年的那个安徽中考题，他的那个第十题的压轴题的答案呢，也是 a 选项，如此一个类，一个意思啊，一个意思，但是他也是，呃，有一个审题的一个关键点。好，那这样的话，我们 a 选项呢，就不在这方继续讲了，继续我们看 b 选项， b 选项的话，它点 d 在 边 bc 上运动的时候，问我们正方形 a、 d， e、 f 面积的最大值，那 b 选项很简单， 这个正方形是不是等于 a d 的 平方，所以 a d 最大的时候呢，它整个面积就最大。那很想这个 a、 d 是 不是有一个直线形的距离，就是一个线段，那它距离最大的时候，肯定到 a b 的 时候是最大，所以那个 b 选项它是对的啊，所以这个 s 的 最大值呢，刚好等于二倍根号二括号的平方等于八。 c 呢？我们再看 c， c 是 点 d 在 这条边上运动的时候， b m 的 这个最大值是二分之一，我们知道这个地方是个垂直，所以这个图里面会形成一个一线三等角， 这有个一线三等角，这种题目在做一线三等角的题目的时候应该接触过，对吧？我要求一下 b m 的 这个最大值，那这个地方呢，我们就可以几何转代数啊，几何转代数， 那这条边呢，是二，我们可以设个圆就可以了。设这条边是 x， 那 这条边呢，等于二减 x， 把 b m 呢设成 y， 我 们知道这方有一个一线三角的相似，那熟知一线三角相似的乘积式的结论的同学，这方就可以直接写了啊， 或者你把比例式列出来，那我们直接写乘积式，应该两个 y 等于 x 乘上二减 x， 那 这方把 y 呢写出来，应该等于二分之一， 这个负的二分之一 x 的 平方再加上 x 配方就可以了。那就是负的二分之一 x 的 这个平方再减二， x 再加一，再减一，等于负的二分之一 x 减一，括号的平方再加上二分之一。所以 当这个 x 等于几时？等于一时，它的最大值呢？等于二分之一一，刚好呢，在这个取值范围上面，对吧？好，所以 c 答案呢，也是对的啊。这题比较难的是这个 d 选项啊，像有很多同学当时呢可能没有办法很好的处理这个 d 选项， d 选项呢，是一个模型， 这模型大家可以学一学啊，就是目前像咱们安徽的话，考的不是那么多啊，不是那么多，它是一个斜大于直的模型。斜大于等于直来讲一下啊，那 这个三角形是一个直角三角形，那这种题目呢，因为我们要求 a n， a n 刚好是这个直角三角形的斜边，对吧？我们遇到直角三角形的斜边，我们可以考虑取一下 a n 的 中点，取 a n 中点 o， 我 们取一下它的中点 o。 啊，这个地方的话，嗯，图不一定很准啊，就差不多这是点 o。 好， 这是它的中点，那显然的话， o d 是 不就是这个？呃， o n 的 这个 a n 的 一半，所以它是等于二分之一 a n。 好， 那这时候我们可以设个圆，把 o d 呢设成 x， 把 o a 呢也设成这个 x， 那么我这时候我再过 o， 那 向这再做一条垂线，在这再做一条垂线，把垂足呢标为点 h。 很 显然，此时我是不是形成了一个直角三角形 o d o h。 现在的话， o d 在 这里面是不是作为它的这个斜边，而 o h 呢，是作为它的这个什么边，这个直角边，显然这个 o d 的 话，它一定是大于这个 o h 的。 那什么时候能等于 o h？ 就是 当这个地点和这个 o 点，就是这个 h 点和这个地点刚好重合了，那此时 它的这个斜边呢，刚好肯定是等于这个 o h 的。 有时候这方有一个取等的过程，有一个取等的这个这个过程。好，那这时候我们就把这个 o d 和 o h 用我刚才射源的这个量给它表示进去啊，所以 x 呢，就大于等于。我们看一下， o h 等于呢，我们射的这条边是 x， 因此这个 o b 这条边呢，它应该等于二倍根号二，再减 x， 而这个地方 o h b 始终是一个等腰直角三角形，所以我的 o h 应该等于这条边，再除以根号二，所以它就大于等于 根号二分之二，再减多少减 x， 然后把这不等式解出来，那就根号二 x 大 于等于二倍根号二，再减 x， 把不等式解一下啊，那就根号二，加一倍的 x 大 于等于二倍，根号 x 应该大于等于二倍根号，除以根号加一分母由里化， 那又变成的是根号乘以这个根号，再怎么样减一啊？减一这括号打不下去了，那应该等于多少？所以的话应该是 x 大 于等于这个四减二倍根号，而我刚才说了这个 o d 呢，它是等于 a n 的 这个一半，因此 a n 的 话就应该大于等于八减四倍根号，所以 d 答案呢，它也是对的啊。所以这题大家重点学习一下 d 的 这个模型的一个处理的方法。

接下来呢，我们去看第二十三题的几何压轴题，老规矩，还是先读题，他说这个问题情景，在数学活动课上，老师呢，提出了如下问题，将图一中两个全等的直角三角形直板 a、 b、 c 和 呃，这个三角形 e、 b、 d 重合放置，往下翻一翻，找找图哈，那我们往下翻一翻，看到这个图一的位置哈，然后呢，其中这个 a、 c、 b、 e、 b、 b 都是九十度， a、 c 的 长度呢，和 e、 d 的 长度重合是四， bc 和这个 b、 d 的 长度重合是三，也就是说这个三角形，而两个三角形啊，都是什么呀？都是三四五形三角形，对吧？我们这写一下要小心哈，三四五形三角形比较特殊，后续用法过程可能会用到哈， 然后呢，将三角形 e、 d、 b 绕点 b 进行顺时针旋转，旋转角度为 r 法呢，这个度数哈，然后呢，如图二，当什么呀？当 b、 d、 e 这个三角形的直角顶点 d 恰好落在边 a、 b 上的时候， 然后 e、 d 的 延长线交 a、 c 与 d、 f， 然后是判断 d、 f 与 f、 c 的 数量关系啊，数量关系重点啊，然后呢，并说明理由。然后这个问题一，请解决老师提出的问题，这个就比较简单了，数量关系无非就是那么几种嘛，对吧，我们常见到的相等 是吧？这道题目里面比较简单的这个证法就是什么呀，连接 b、 f 去证 b、 d、 f 和 b、 c、 f 是 全等关系。这的话，我需要给你去分析一下一个条件哈，因为本身前提条件现在已经给我了，叫做 b、 d 等于 bc， 然后呢，这个 呃， e、 d， b 等于 a， c、 b 等于九十度，这已经有两个天然性条件，我要去证 d f 和 c f 的 数量关系，那我把它放到两个三角形里面的话，那直接点 b f 做公共边就可以了，对吧？所以我直接 把 b f 给它连起来，然后呢，去证明三角形什么呀？然后去折三角形 b， d， f 全等于三角形 b， c f， ok 吧？呃， h l 定律啊， b f 做公共边， b c， b d 相等九十度，然后挣到权呢，以后的话就可以得到谁了，就可以得到 d f 的 长度和 c f 的 长度，它是对应边相等， ok， 第一问结束之后的话来看，第二问，他说将三角形 e， b， d 接着绕点 b 进行旋转，旋转到图三的位置，然后呢？做射线 c d 啊，做射线 c d， 然后呢？ 呃，交 a e 与点 n， 然后此时这个小组的同学认为 n 点是 a e 的 终点，请判断他的观点是否正确，并说明理由。我们常规性的这个判断方式的话，我要去判断终点， 就是要去正 e n 等于 a n， 也就是说我这道题目要判断是否为终点，我们给他转换一下证明的这个结论。我只要能够正到什么呀？正到 e n 的 长度和 a n 的 长度是相等的， 是不是我就能够得到 n 点是 a e 的 中点了，对吧？那我们要去证明这两个角度相等，依旧是常规性方法，要么找全等，要么呢去利用特殊关系，然后去 呃，证明他， ok 吧？那这个题目里边的话，我们相对来说不太好做的就是这一点，因为他本身题目里面并没有给到我过多的信息。那我反过来要去正中点的话，我们其实可以用一下逆向思维，我们在我们在有终点的前提条件下，我们的做法相对来说就会比较多了，对吧？ 比如说我可以做中位线，我也可以做背长中线，那反过来，如果让我去正中点的话，那我是不是依旧可以假借这个信息，然后去给他做一个这个思路？ 那我们这的话，因为他本身没有什么中位线性的信息，所以我这先不考虑中位线，然后呢去给他做什么呢？做这个背长中线，那既然要做背长中线的话，那我就直接去连就好了，对吧？ 连就好了，然后呢把 c n 他 已经给我连下来，这条线呢？给他延长出去。延长出去以后的话 到底要延多长？有交点就行哈。与谁有交点呢？叫过点 e 做 a c 的 平行线，有交点就行，为什么？因为我要去做一个八字全等，然后呢以八字全等帮助去干什么呢？证明这个全等就可以了。那我们这标一个 m， 也就是说我只要正到 m e n 和这个，呃， c n 这两个三角形是全等的，那是不是就可以正到我想要的 e n a n 对 应相等， 对吧？那关键信息来了，我在做辅助线的时候要说明清楚，我要延长 c n 过点 e 呢？做这个 e m 平行于 a c 交 c n 的 延长线于点 m， 那 这个时候的话有平行角相等啊，因为本身这个地方是有对应角相等的，对吧？ 有对顶角相等，还有什么呀？我们答内错角相等，对吧？内错角相等，那这个地方的话还有一个内错角在这里， 对吧？还有个内错角在这里。然后的话我们去关注一下，我想要这两个三角形，全等三个角都过来，但关键问题是我想要正全等是缺边长条件的，那我想要去正边长条件，有没有信心？ 这我们要去关注一个点，叫做我做射线 c、 d 交 a、 e 于点 n， 那 这个时候的话，相当于是我是把 c 和 d 这两个点连起来之后延长出去的，对吧？那这个时候的话，我们要知道 bc 和 b、 d 这两条边角对应边， 是啊，本身就相等的，那我连起来以后的话，代表着三角形 b、 c、 d， 它是一个等腰三角形呀，那等腰三角形以后的话， b、 d、 e 又是个九十度，那我这就可以去假借谁的呢？叫假借啊， 九十度的互余关系，帮助我去证明线段相等，来看一看我这是怎么去正的哈。首先呢，我们知道 b、 c、 d 的 话，它是一个等幺三角形，那说明等边对等角是不是就有了什么了？叫做这个角和 这个角是 b、 c、 d 和 b、 d、 c 这两个角度是相等的。然后呢，我们要去注意 b、 d、 c 加上 edm 这个角度正好是个互余关系，也是相等的。然后呢，同时这个 b、 c、 d 加上 a、 c、 n 又是一个互余关系，也是相等的， 能不能反应过来叫等角的与角相等吗？所以我们会发现 a、 c、 n 和什么呀？和 e、 d、 n 这两个角度它是相等的。哎，这个时候我们再关注 我这打双杠的角度是不是就出现了三个？首先的话，我们刚开始给到的平行线内错角相等，角 m 和角 a、 c、 n 就是 相等的， 然后这个时候我又通过等角的与角相等，从而推到了 a、 c， n 和 e、 d， n 这两个角度是相等的，那从而得到的在三角形 e， m， d 这个三角形里边叫等角对等边，我们就可以得到 m， e 和 b， e 是 相等的。然后呢，由我们刚开始题目当中给我们的体概念信息叫做 e， d 和 a， c 是 对应边相等，从而正到什么呀？正到 m， e 和 a， c 是 对应相等的，那这样的话，我在三角形想，正的这个三角形 a， c， n， a， c， n 和三角形 e， m， n 当中 除了有三个角对应相等，我要两个就可以了，对吧？以及我正到的 a， c 和 m， e 是 对应边相等的，是不是就从而正到了这两个三角形全等， 对吧？这两个三角形全等以后的话，是不是就有了对应边相等倒过来就正到了 e， n 等于 a n， e， n 等于 n n 以后的话，我就可以得到 n， 是 啊， a， e 的 中点， ok 吧？这是我们假借被场中线的这样一个思路去 帮助我去正中点的，正好是一个逆向思维的去做法哈，那这个呢，就是第二问。好，第二问结束以后的话呢，我们再看第三问，他说当三角形 e， b， d 再绕点 b 进行顺时针旋转的过程当中，连接 a， d， a， e 是 否存在某一时刻使得三角形 a， d， e 是以 a， e 为直角边的直角三角形啊？那我们要连接 a， d， a， e 以后去关注这个三角形了，那我这给了两个图哈，正好是在它旋转一周的过程当中所形成的两种特殊情况，那如果存在呢，请直接写出此时 a， e 的 长度，若不存在，请说明理由，那这的话就， 嗯，存在是肯定存在的了，对吧？我图都给大家画出来了，然后我们就借这两个图去算一下 a、 d 的 长度就可以了， ok 吧？那第一种情况当什么呀？当这个，呃三角形 b、 d、 e 还在 b、 c 这条直线啊，在它左半边旋转的时候，我们要此时达到什么呢？叫做 a e 是 a d e 这个三角形的直角边长，呃，直角边，对吧？那这个时候的话，我们会发现它有一个旋转前后的对应边关系， 叫做 b e 和 b a 是 对应相等的，那就间接告诉我这个三角形 b、 e、 a 是 一个等腰三角形，我们有等腰三角形要去小型等腰三角形，它其实是有什么呀？有 三线合一的嘛，对吧？所以我们还是去借助等腰三角形的三线合一帮助我去求这个题。那我们把这个三线合一给他画出来，三线合一画出来以后的话，这个地方是有垂直的， ok 吧？我们还是去 呃标一下这个字母吧。那我们把这个地方呢？还是给他标一个 m 吧，常规性习惯用的一个字母哈。然后的话，我们在这个呃 bm 这条三线合一的基础之上，我们去倒回去分析我们能得到的某些信息啊。首先第一个 三线合一有垂直，所以 emb 是 九十度。我们刚刚说过了，我在旋转的过程当中，我要使得 a、 d、 e 是 一个以 a e 为直角边的直角三角形，那此时这个直角三角形的直角在哪里呢？在 a、 e、 d 上，也就是说 a、 e、 d 此时这个地方是一个九十度， ok 吧？那我们就会发现一个问题，叫做 a、 d 的 这个位置关系和 b、 m 的 位置， 这个，然后这个时候的话，我们就会发现 a、 d 和 b、 m 它的位置关系的话就是一个平行关系，那此时因为 m 点的话，做三线合一的交点出现，那 m 正好是 a、 e 的 中点，那说明平行关系以后有一比二，那这个时候 bm 与 a、 d 的 呃， b， m 与 e、 d 的 交点，我们标一个字母哈，我们标一个 f 吧，标一个 f 哈， m f 的 话就是这个三角形 a、 d、 e 的 中位线，那 f 的 话恰好就是 ed 的 终点， 那此时的 m 这个 f 的 话就是 e、 d 的 中点， ok 吧？表哥，相当题目当中刚刚告诉过我们， e、 d 的 长度的话是等于四的呢，中点的话就各是二，对吧？各是二，然后的话继续 三角形 abc 也好还是 b、 d、 e 也好，都是三四五型三角形本身它的三四五是存在的，所以这个地方是三， ok， 这个地方是 五，就是 b、 d 的 长为三，然后 b、 e 的 长为五，那这样的话我们本身在三角形 e、 d、 b 这个直角三角形里边， b、 d、 e 就是 九十度，然后还给了我，或者说我推出来了这个 d、 f 的 长度是二， b、 d 的 长度已知本来就是三，然后通过勾股定律的话，我们就可以求出来， b、 f 的 长度的话是一个根号十三，对吧？是一个根号十三， 然后的话我们要去求这个 ad 的 长度，其实直接求 ad 也行，然后间接 先求 m、 f， 再求 ad 也行， ok 吧？然后的话我这是先求的中位线 m、 f 的 长度，因为这个三角形比较好看的原因在哪？哈？这个地方是 b、 d， e 是 九十度，然后呢？这个，嗯， b， m、 e 也是九十度，还有一个对顶， 还有个对平角，对吧？然后这两个三角形的话一定是相似的，那相似完以后的话，我就可以直接去呃，求这个什么相似比了，对吧？那相似以后，我这哎写下吧，叫三角形 b， d、 f， 和什么呀？ 和三角形 e， m、 f 是 相似的，然后呢，我要求的是 m、 f 的 长度，所以我们先求 m f， 对 应边的话是 f， 对 应边的话是 d f， 已知的线段长度呢，是 e f， 然后呢，对应的边长是 b f， 我 就可以得到 m f 的 长度， 对吧？然后我们求出来的 m 长这个 m、 f 的 长度，呃，这还是老规矩哈，大家自己往前带一下数据去算一下就可以了，我这直接给答案哈，这算下来的话，正好是一个这个十三分之四倍，根号十三 啊，十三分之四倍，根号十三。然后 m、 f 的 话恰好是 a、 d 这个长度的一半，所以 a、 d 的 长度的话，就等于二倍的 m f， 也就等于多少呀？等于十分十三分之八倍，根号十三。 那这个呢，就是第一种情况，第一种情况结束以后的话，我们来看第二种情况，也就是我再再继续往这个顺时针方向往右旋转，旋转到， 呃，三角形 b， d， e 恰好落在这个线段 bc 右侧的时候，它又有一种情况，叫做以 a e 为直角边的直角三角形。 那此时的话，我们要注意，本身三角形 b、 d， e 就是 一个直角三角形，而且叫 d， 是 九十度，对吧？然后呢，我现在又是以 a、 e 为直角边长的 a、 e、 d 又是一个九十度，它也就是平行关系，所以这个时候的话，我为了方便计算的话，把这个不规则型或者叫把这个 直角梯形给他补成一个我们比较熟悉的图形出来啊，往外延一下，给他补一个什么？给他补一个这个这个矩形出来，好吧，比较熟悉的一个图形 补一个矩形出来，相当不太好看。做垂线， ok 吧？做垂线哈。然后呢，我们形成一个矩形，形成矩形以后的话，我们就会发现这个 b 点的话，恰好是， 嗯，标个 n 吧，没用过哈。然后这个焦点标点 n， 那 此时的 b 点的话，恰好正好是 d、 n 这条线段长度的中点， ok 吧？正好是中点，我们可以用全等去正一下哈，用这个 a、 b、 n 和 e、 b、 d 这两个三角形全等去正哈。正完以后的话， b、 d 的 长度和 b、 n 的 长度是相等的，都是等于几啊？都是等于三，那 这个 a、 n 的 长度和 d、 e 的 长度相等等于四，那说明 a、 e 的 长度就等于六，对吧？ a 的 长度和 d、 n 的 长度相等的嘛，就等于六，那这样的话我再去求 a、 d 是 不直接一步就出来了， 对吧？所以这个一步的 a、 d 的 长度就直接勾股就出来了，就是个二倍根号十三，不需要花费多长时间啊？ ok， 那 这样的话我们就把两种情况都给他算出来了，所以算出来以后的话，上面要给他一个结论的话，叫综上所述， ok 吧，因为他是直接写出吗？我们这可以直接答的哈，综上所述 所数，这个 a、 d 的 长度的话，要么是等于一个十三分之八倍根号十三，要么呢？是等于什么呀？等于一个二倍根号十三， ok 吧？那这个呢？就是两种情况所得到的答案，那这个呢？是二十三题的几何压轴题，如果还有别的问题的话，我们可以私信探讨， ok。