七上数学三角板旋转问题技巧
粉丝22.6万获赞109.4万
相关视频
 03:13查看AI文稿AI文稿
03:13查看AI文稿AI文稿本月期末考试十二分的压轴题必考,这种冻脚问题一定收藏保存给孩子看,考试遇到不丢分!这道题难度非常的大,综合了两个压轴考点,第一个是双脚平分线运动,第二个是冻脚中的适而不求方法。 今天韩老师用一个视频带你彻底学会这两种题型韩老师已经全部整理好了, 拿去给孩子练习,期末考试轻松多考二十到四十分。我们一起来看这道题。直角三角板,直角顶点 p 在 直线 c d 上, a 和 b 在 c d 的 同侧, 当角 a p c 是 四十度的时候,问角 b p、 c 是 多少度?这个非常简单,就是用平角减去四十度,再减去直角顶点九十度,所以它等于五十度。第二个问 pm 平分角 a p c p n 平分角 b p d。 求角 m p n 的 度数,那这就是一个非常典型的双角平分线模型。遇到这种题,直接用设而不求的方法,我就设 角 a p m 和角 m p c 都等于 r 法,角 b p n 和角 d p n 都等于贝塔,那于是乎根据平角,我们可以列出一个等量关系,就是两个 r 法加上九十度,再加上两个贝塔是等于一百八十度的,那我不能求出 r 法加上贝塔就等于四十五度, 要求的是角 m p n 这个角的度数。角 m p n 其实就是由 r 加九十度再加上贝塔构成的。 而我刚才已经求出了 r 加贝塔这个整体,直接带入进去就等于九十度,加上四十五度,那么就等于一百三十五度。会发现这是动角问题中的一个定值问题,不论咱们的角 a、 p、 b 怎么样,旋转的时候只 只要左边有角平分线,右边有角平分线,那么这两个角平分线之间的夹角一定是一个定值,即为一百三十五度。那这里我们也用到了适而不求的方法,那根据这个方法,我们 可以继续求解第三个问题。如图三,当点 p, 让三角板 a、 b、 p 继续旋转,使得 a 和 b 在 c、 d 的 异侧, a 在 上方, b 在 下方。当角 a、 p、 c 是 四倍的角 b、 p、 d 时,求角 b、 p、 c 有 多少度?那这道题 我们依然可以继续用适而不求的方法。我就设角 a、 p、 c 为 x 度,那我就可以通过已知条件把 其他的角给他表示出来。那么此时因为角 c、 p、 d 等于一百八十度,那么角 a、 p、 d 就 应该等于一百八十度减去 x 度。那么同理, 角 a、 p、 b 等于九十度,那角 d、 p、 b 就 应该等于九十度,减一百八十度,减 x 度,所以它就是 x 度减去九十度。那么接下来呢?我们就根据题目给到的等量关系,直接列方程就可以了。 x 度是等于四倍的 x 度减去九十度,那所以说 x 就 应该是等于一百二十度, 那么 x 既然等于一百二十度,所以角 d、 p、 b 是 不是就应该等于一百二十度减去九十度,等于三十度,那么角 b、 p、 c 是 不是其实就是角 d、 p、 b 的 一个补角,所以它应该等于一百五十度,所以它的值也是一个定值。这两种题型你学会了吗?
579韩佳老师数学方法 05:15查看AI文稿AI文稿
05:15查看AI文稿AI文稿本期视频我们来讲解期末压轴的动角旋转问题。分析条件,点 o 为直线, ab 上一点 过点 o 去做了射线 oc, 并且 boc 始终都是六十度。一个三角板的直角顶点放在了 o 这个地方,那我们就知道了,图中的角 m o n, 它就是九十,所以 m o c 我 瞬间就能读出来, 不就是九十减去六十等于三十度吗?好,来看问题。第一个,当我们的三角板 m o n 的 一边 o n 与射线 o b 重合时,求 m o c, 哎,我们在梳理条件的时候是直接求出来了,就是九十度减去六十度,所以等于 三十度。好!第二个问题,将三角板 m o n 绕着点 o 逆时针旋转至图 三的时候,并且告诉我们角 n o c 等于五度。好,中间这个非常小的夹角是五度,让我们去求 a o m 的 度数。好, a o m。 我 们来观察一下要求 a o m 的 度数,我们需要知道的是, m o n, 哎,这是九十度,再加上 n o c 五度,哎, b o c 的 度数你知不知道 它是固定不变的六十度,所以我们得到了一个平角方程对不对?隐藏条件,一条直线, 哦, a o b 就是 一百八十度,所以角 a o m 就 等于一百八十度。把其他角全减去九十度,再减去六十五度,等于九十减六十五,当然是二十五度, 好,关键。第三问,如图二,将图一的三角板 mo 绕着点 o 进行每秒钟十五度的速度, 逆时针方向旋转一周非常重要。第一个,我们知道了它的速度为是等于十五度每秒的。第二个,我们知道了它的运动时间 t 旋转一周大于对零小于等于哦,三百六十除以十五等于多少?哎,二十四。换句话说,我等会要求解出来的时间一定要在这个范围内。他说,在旋转过程中,当 直线非常重要, o n 恰好平分锐角 b o c 时,旋转的时间是多少秒?好,怎么去处理这个问题?我们要找的是什么? b o c 的 角平分线对不对?那管他三角十一,我先把他的角平分线先做出来来, 他的角平分线在这个地方,对不对?换句话说,我们的 o n 对 吧,一定是和这条直线重合的 是不是?那我们知道 o n 在 旋转的时候,哎,他可以哦,转到这里的时候和上半部分进行重合,同理啊, v 可以 转到下半部分和 这个部分进行重合,所以有两种情况哦,这个时候你就知道为什么要给时间的范围,对吧?要看一看这两个时间是不是都在这个范围内啊?好, 那么既然你告诉我 o n 是 b o c 的 平分线,那我要看整个三角板旋转吗?不用, 记住问题,我们思考的是什么?把问题怎么去简化,而不是复杂,它表面给的是什么?哦,表面给的是三角形 m o n 去进行 旋转。但是第三问这个问题,最终我要把它转换成什么?仅仅是 o n 进行旋转,对吧?你看一条 直线、射线或者线段的旋转远比一个图形的旋转要简单的多,因为我只要它旋转就够了,对不对?好,你看啊,第一种情况,我们的 o n 从哪里开始转的?从第一幅图开始,也就是我要标出它的起始边 来, o n 是 在这里转的,那第一种情况哦,转到哪里啊?哎,转到这里转了多少度啊?哦,转了 b o c 六十度始终不变吗?那不就得转一半三十度吗,对不对?所以第一种情况,哎,直接我们的时间等于 路程除以速度,对不对?速度每秒,所以直接两秒钟搞定。那第二种情况呢? 哎,说了哦,我们的边转到哪里来?哎,转到从这开始,一直转转转,转到这里和它重合,对不对?那我们来看看 转了多少度啊?哦,转了一个三十度,再加上一个平角一百八嘛,对不对?所以转了多少度?哦,二百一十度,是不是?所以来 t 等于二百一十?那我们直接用一百八十度加上三十度去除以多少?二十五度每秒, 对不对?那不就是十二再加上多少三十除以十五二吗?所以等于哎,十四秒。 ok, 好, 那么本期视频就到这里,大家拜拜。
130小鱼数理化 06:13查看AI文稿AI文稿
06:13查看AI文稿AI文稿家人们注意了哈,动脚问题一定是我们期上期末考试必考的亚洲王,其中啊,三角板的旋转问题更是难倒了一大片的孩子,像这道题啊,听说全班做出来的人没有几个,我们来看一下,一步三角板,如图,放置三角板 a, c, d 啊,绕着 a 点 以 m 度每秒,顺时针啊,顺时针方向旋转,同时三角板 a、 e、 d 绕着这个 a 点逆时针旋转,速度是矮盈度每秒。 当 a、 b 和 a d 啊首次重合时, a、 b 和 a d 旋转的时候,首次重合时就停止运动了,说当角 m m a d 等于六分之五倍的角 c, a, e 的 时候, 说求 m 与 m 的 关系。那拿到这样题,首先我们要把动角问题转化成数轴上的动点问题,那么我们的思路就会很清晰。好,那既然动点呢,我们要有什么圆点?我们假设 a n 为圆点,是吧,记作零度,那么 a m 的 话 就是个一百八十度。好,然后我再假设顺时针方向,为什么方向呢?正方向啊,当然喽,你也可以假设什么啊,顺时针为正方向,我们也可以假设逆时针,为什么正方向都是可以的?好,我们假设啊,逆时针方向为正方向, 那么 a n, a e 射线 a e a d a b a c 这些射线所对应的什么度数,是不是都可以表示出来了,对吧?所以第一步我们就要表射线, 我们把所有的射线表示一下,这里涉及到旋转问题,同时没有旋转时间,所以我假设啊,旋转时间为什么 t, 是 吧,旋转了 t 秒。刘 老师,那最后 t 的 话怎么办?我们可以有一种方式思想,叫做什么适而不求的思想啊,所以先不要怕我们把它表示出来啊,那么来看, a e 起初是在零这,然后它是绕着 a 点旋转,旋转的速度是 n 度为秒,所以 a e 啊, 一秒钟旋转 n 度 t, 一 秒就旋转了什么 n 度 t? 是 不是?那么 ad 的 话, ad 初始位置是三十, 沿着正方向旋转加也旋转了 n 度 t, 所以 加上 n 度 t, 好, 这是射线 ad 的 位置,那我们再来看一下 am 出来了, ac 射线 ac 怎么表示? ac 的 话,初矢位置是记在一百八,它沿着顺时针方向,逆时针记作正,那顺时针是不是就负了啊?那就向这边来的话,就要什么减,向负方向我们去什么减?好,一百八, 一秒钟旋转 m, 读 t 秒钟旋转 mt, 所以 说 ac 的 话应该是一百八减去 m 度 t, 那 我把 ab 也给表示一下啊, ab 的 话,呃,这是一百八,然后这是四十五,那这个位置的话是一百三十五度,对吧?然后向负的方向是不是旋转,也就是一百三十五度,要减去 m 六 t 是 不是它也旋转了 mt, 好, 那有了这些线的位置,第二步我们就去什么第一步表示线,第二步求夹角 啊,把我们要求的夹角给表示出来,也就角 m a d, 我 们来看一下角 m a d, 我们来看观察一下角 m a d 是 吧?已知大小大减小,位置大小差绝对 m a 和 a d 是 不是 a d 要比什么 m a m 要什么小,是不是啊,因为这边是正方向啊,然后它大的话,我们就拿大减小,然后一百八, 一百八十 am 一 百八,然后减去 a d, 减去括号三十度,加上 n o t, 也就等于一百五十度,减去 n o t, 是 不是好?这是角 m a d, 再来表示角 c a c a c a e。 好 明显的 c、 a 是 永远比 a、 e 大 的,因为当这两条线重合时,是不是停止运动了,也就 ac 始终是比要这个 a e 要什么大,所以我就拿 ac 的 位置减去什么 a, e 的 位置是不是好? ac 的 话是一百八十度, 减去 m 度 t, 再来减去 a e a e 的 话就是 n 度 t。 好, 这是 c a e, 这是 m a d。 好, 这两个有什么关系呢?所以说叫第三步,列方程 好。第三步,我们来列方程,根据这个等量关系啊,我们把方程列出来解一下啊,也就是角 m a d, 也就是一百五十度减去 n 度 t, 要等于六分之五倍的,是不是它 啊?角 c e, 也就是一百八十度,减去 m 度 t, 再减去 n 度 t。 好, 我们来看一下,先去分母,两边同时乘以六,也就是这乘以六的话是九百 度,减去六倍的 n 度 t, 等于五倍的它,也就乘以它五倍的括号一百八十度,减去 m 度 t, 再减去 n 度 t。 好,我们去下括号九百度,减去六 n 度 t 等于九百,减去五倍的 m 度 t, 再减去五倍的 n 度 t。 同学们来看一下,两边都有九百, 是不是消掉了 n 度 t? n 度 t 移过来来,也就是负移过来,是不是加,也就是负六,加上五,也就是负 n 度 t 等于负五倍的 m 度 t。 朋友来看一下,我们刚刚设了 t, 但是我们有没有参加我们最后的计算,是不是没有叫设,而不求 t 和 t 消掉了,符号和符号消掉了,那我们就得到 n 等于五倍的什么 m 是 不是好?也就是 m 与 n 的 关系。我们是不是找到了 n 等于什么?五倍的 m? 这就是事而不求的思想来解决三角板的,是吧?旋转问题。好,你学会了吗?关注刘老师,学习路上不迷路。
 04:33查看AI文稿AI文稿
04:33查看AI文稿AI文稿这道题太难了,就这种动脚问题,难倒了咱们百分之九十的同学。其实我们动脚问题解析是有技巧的,我们原模原样利用之前我教大家数轴上动点问题解析的三要素四部曲,就可以轻松求解这类动脚问题。 那有关于动角问题,这里常考的五大题型,我都给大家做了一个系统的总结,历年的真题都在这了,那么我们动角问题这里五个题型,每类题型都是有方法的,你把通用的技巧搞定了,那这种题目真的咱们是个个能拿满分的,并不难啊。 下面呢,老师就带着大家通过这道题,一起把我说的三要素四步法再来一起复习一下。这里告诉你,角 a o b 这个角呢,是一百二十度哦,它一百二十度。 现在说了,射线 o c 从 o a 开始绕点 o 逆时针旋转, o c 是 这么转过来的,速度为每分钟二十度,那 t 时间它就转动这么大的角度呗。 o d 呢,从 o b 开始绕点 o 逆时针旋转,它就这么转呗,速度为每分钟五度,那 t 时间不就转动这么大的角度吗? 他说了两条射线同时旋转,旋转的时间在这个范围内, t 为和值时,两条射线重合。 那什么叫做两条射线重合呀?它像不像我们之前那个竖轴的动点问题?这是一个竖轴,这是点 p, 往这动二十 t, 这是点 q, 往这动五 t, 像不像竖轴上的一个锥级问题啊? 他在角,这他不也是一个追集问题吗?把角拍平了就行呗。所以啊,我教大家用竖轴的思想来解决动角问题,特别容易看,在这我建立一个旋转竖轴,那么同样我把竖轴的圆点标出来,这就是正方向, 那对应 oc, 咱们就可以看作一个从圆点出发,向竖轴正方向运动的点了,我们把射线拍平了再去看,所以射线 oc 运动 t 时间之后的位置,我们就可以用零加二十 t 来表示。 同样啊,我们由于 o b 是 一百二十度,这是那个一百二十度的位置,那我们 o d 对 应这条射线,就是从一百二十度这个位置出发,向正方向运动,用加法运动了五 t 个单位长度, 射线运动 t 时间之后到达的位置咱们都表示出来了,接下来我们要研究两条射线重合,那怎么办呢?让它俩直接相等就可以了,所以我们就有二十 t 就 等于一百二十,再加上五 t, 那 在这啊,我们计算一下,就可以求出 t 等于八。第一个问咱们就很容易的解出来了,继续来看第二个,问问你 t 为何时 c、 o d 等于九十度来? c、 o d 是 什么? 是不是由动点 c 和动点 d 组成的这个夹角啊?它其实在竖轴上,不就是让你求这两条动点之间的距离 是九十吗?对不对?所以角的动态问题,我们就把它拍平了,看成点的问题,求角等于多少度,就是在求这两点间的距离呀, 所以对应我们已经把射线运动 t 时间之后的位置表示出来了,那对应这个角 c、 o d 就 可以用它俩求距离。怎么求?距离?已知大减小,未知察觉。对, 看看 o c 和 o d 谁在前谁在后啊?来,这是正方向对不对?刚开始的时候 c 在 后, d 在 前, 但是运动一会,由于 c 的 速度快,他是不是就把 d 给追上了,所以他俩的大小关系是不确定的。那我们要求他们俩之间的距离是不得加绝对值啊,是不是用一百二十加上五 t 再减去二十 t 的 绝对值表示啊? 那不就是我们一百二十再减十五 t 的 绝对值吗?这就是角 c o、 d 的 度数,我们直接令它等于九十,就可以求出 t 的 值。了 解这个绝对值方程会吧,我们直接分类讨论,第一种,一百二十减十五 t 等于九十。 第二种,一百二十减十五 t 等于负的九十,代入求解,再利用对应的时间进行检验就可以了。那接下来的时工作啊教给大家了,请你来算一算时间 t 到底等于多少吧。
521依依老师讲初中数学 11:53查看AI文稿AI文稿
11:53查看AI文稿AI文稿期上数学期末压轴必考的就是冻脚问题,看见冻脚问题就想跳过的同学有救了,去老师用一个冻脚问题理清思路,冻脚问题不再丢分。第一个就是看到这道题生理反感,第二就是不知道怎么下手。好,来我们看看啊!如图一,将一副直角三角板 放在直线 a、 d 上,哎,左边这个和右边这个,这都是标准的三角板啊!然后现在告诉我们一些具体度数,什么 o b c 等于九十, m o n 等于九十, b o c 等于四十五,那说明这个就是标准的等腰直角三角形 m n o 等于三十,哎,说明这是三十,这是六十,是吧?保持三角尺 o b、 c 不 动,将三角尺 m、 o、 n, 哎,就这个右边这个,他要绕点 o, 以每秒十度的速度顺时针旋转啊, 这样去转,旋转的时间为 t t 是 在零到九秒。好,其实我们可以先开始在这先审一下他,既然速度是十二,一共要转最多九秒,是吧?哎,所以他最多转多少? 十乘以九九十度,对吧?那转九十度,这个 m o n 转到哪去了?转到这边了,到这边了,哎,就是 n o 是 不是正好跟这个 o d 这条边重合了,对吧?那 m o 是 不是正好转到垂直这个位置了,对吧?转了一个九十嘛?先看第一问啊,当 o m 平分角 b o c 的 时候, om 平分角 b o c 的 时候,求 t 的 值,那这个倒比较简单了,是吧?我们是不是只需要考虑 m o 这条线,它转到这个位置是不是就行了 啊?他转到这个位置,我们需要知道就是他转了多少度吗?那既然你这个角 boc boc 是 四十五,那一半 就是二十二点五,对吧?你撞了二十二点五,你的速度是十,所以我们应该用二十二点五度除以十度每秒,那就应该是二点二五秒啊,这道题就做完了。好,再看第二个 判断, m o c 和 n o d 的 数量关系,其实同学们基本上就是在这啊,在这他们会蒙, m o c 是 这个角吗? n o d 是 这个角,很多同学就蒙了嘛,对吧?目测一下啊, 祖传的目测大法是吧?哎,觉得这个角是这个角的一半,对吧?哎,错了,肯定不对啊。我们如果要去聊清楚 这个东西,首先我们需要先想一想啊,它是不是要分类讨论,那得吧,它绕过去那个了, o m 就 在 o c 的 这边。哎,对了,其实我们在聊的是 m o c 在 聊什么? m o 和 c o 这两条线,它们俩组成的角 就这两条射线,它俩有没有什么位置的变化?有的,因为 m o 有 可能转过去了。再看 n o d, 你 也得看看那 n o d, 它是哪两条射线的关系呢?应该是 n o 和 d o, 它俩有没有可能会出现什么转过去的情况呢? 没有,没有,因为最多赚九十多,所以这个是不需要聊,就只需要聊他,聊他就应该分一种情况,聊聊,聊他就应该分两种情况,对吧?哎,对,好,我们现在已经把两个图都已经分别画完了,我们接下来需要从每个图里面去分析两个角的关系,这个角和这个角的关系, 对吧?怎么去分析?你直接看图是看不出来的,你需要把这个动角用 t 来表示啊。哎,我们都需要让他们用统一的一个字母来表示,然后你看看能不能把这个字母给它消掉,求出来它一个固定的关系。如果要求这个角,其实这个角 moc 啊,它是跟底下这个角有关系的, 对吧?那 m o b 它就跟 t 有 关,为什么呢?它不就是 m o 从 b o 这,然后转到这吗?所以它的这个角度就是这个三角板,它转的路程啊,相当于是路程,所以应该用速度乘以时间,那是不是就十乘 t 啊?这个就是十乘 t。 好,那这个角度我们就知道了,因为整个这个角 c o b, 他 是四十五。第一种情况,角 m o c 就 等于四十五度,减去十度成 t。 好, 我们再看这个,再看这个, 这个怎么求呢?哎,我们需要想一下 n o 他 此时的运动过程了,那本身 n o 是 在这个位置啊,我把它画出来啊,就在这,是吧?所以 n 变到 n 撇,它转的是这个,这个是不是也是一个十度乘 t, 那 跟它有什么关系呢?九十减去十,哎,加起来等于九十,所以应该用九十减去它,等于它,对吧?所以角 n o d 就 等于九十减去十度乘 t, 我们确实开始的时候看不出来,对吧?瞪眼法是不行的,但是当我把它式子写出来的时候,我天生就知道这俩东西一样,他俩一减就可以消掉 t 了,所以他减,他就应该等于九十减,四十五等于四十五。角 n o d 减去角 m o c 就 等于四十五度。 好,第一种情况我们就分析完了啊,那第二种情况跟第一种情况是不是还是一样呢?看这个图啊,这个图吧, 其实道简单,如果你眼神够好,你真的可以瞪出来啊,一样相等不是?哈哈哈,怎么能是相等呢?肯定不是相等啊,相加等于四十五度。对,那是对的,这个角 c o m 和这个角 n o d 啊,它们俩虽然看不出来一个定量, 但是他们俩如果加上他是一个大定角,那这个角是多少度?是四十五度的补角是一百三十五,对吧?哎,所以他加他加他等于一百三十五,那减去这个九十,就他俩相加应该等于四十五 啊,这个确实可以瞪出来,好,但是如果我们要写的话,你不能这么写啊。啊,你这么写,那学校老师肯定不给分,对吧?瞪眼法怎么写?那你的方法还跟刚才是一样的啊, m o c 应该等于什么呢?你现在要想的是 m o 这条线,他是从 b o 开始,从从这块转的,是吧?这一段是那个十乘 t, 所以减去这四十五,是不是这个?所以角 m o c 就 等于十度乘 t 减四十五。然后我们再看角这个 n o d 啊,这个角,这个角是是不跟刚才一样的 n o 最开始在这,然后他转了这么多,这是那个十度乘 t, 然后九十还是减它,是吧?跟刚才这个结果一样啊,所以角 n o d 就应该等于九十度,减去十度乘 t。 好, 我们观察这式子能不能把这 t 消掉,能相加相加就消掉了,所以角 m o c 加上角 n o d 就 应该等于他俩没了,他俩相加等于四十五。好,那我们就解决完了。第二问啊,如果十二分的话,九分已经拿到了。这个第三问,他不是很恶毒,他要是真的出的恶毒了,就像是 原来四十三或者二十七中那道题就是我们需要讨论的,是好多好多种情况,但这道题还好,哎,这个第三问啊,哎,他又增加了一个运动的元素, 他说在三角板 m、 o、 n 开始旋转的过程中,哎,另一个三角板 o、 b、 c 也开始转了啊,那他是怎么转呢?绕点 o, 以每秒五度的速度顺时针旋转。回想一下,刚才我们那个 m o n, 他 也是绕点 o, 以每秒十度的速度顺时针旋转,他们两个的 这个转动的方向都一样啊,它这边,它也是这边,无非就是它快,它慢啊。好,然后当三角板 m、 o、 n 停止的时候,三角板 o、 b、 c 也停止,嗯, 时间一共就这么多啊,整整个这个跨度不大,然后直接写出在旋转过程中,角 m、 o、 c 和角 n、 o d 的 数量关系。 好,那这种题啊,其实我们前面也遇到过啊,咱们分析的时候就是分析这个角组成它的两条射线 和这个角组成它的两条射线的位置关系。我们先分析 moc 啊, moc 是 由哪两条射线构成的?是 mo 和 co, mo 的 速度快一点,它是十, co 的 速度慢一点,它是五, 那他们两个都是同向的运动,所以 m o 在 追 c o, 对 吧?能不能追上呢?这个就是我们的关键讨论点,是能追上的, 他们两个开始的时候差了四十五度,然后他们俩的速度差是十减去五,所以我们用追击问题的公式,这个四十五除以五应该等于九秒,那就是说直到最后 才追上,所以整个过程其实不需要考虑,对吧?那这个 m o c 不 需要分离讨论,只有一种情况,那么角 n o d, 他 涉及到的是 n o 和 o d 这两条射线,我们看他怎么动 n o 呢?是顺时针在动,对吧? o d 动不动啊? 不动 o d 都不动,对吧?哎,那就是 n o 再往这边走,看能不能追上 o d 能不能追上呢?你整个一共是一个九十度,然后你的速度是十,所以九秒追上, 九秒追上你,最多你时间也到不了九啊,所以追不上,对吧?它也不需要涉及到分类讨论。好,这个题都不需要涉及到分类讨论,我们的难点就在于你如何用含 t 的 式子去表示这两个角。 好,先说第一个啊,角 m o c, 那 我们画一个这个这个图啊,大概去去说一下它们的位置关系,比如说 m o 转到这来了,咱们用 t 的 式子去表示它们的过程啊, 这个角度就是 m o 纯纯的从从从平齐往这转的,所以它的角度就是路程十度成 t。 好, 再说这个角 c o a 这个角度是怎么回事? 它是什么呢?它最开始的时候,你这个 c o 和这个 a o, 它距离是四十五,是吧?但是它又转了一些,转了多少?转了五乘五乘 t, 所以 应该在四十五的基础上加一个五 乘 t。 好, 我们要求这个角 c o m 是 不是就用它减去它就行了?角 m o c 就是 四十五度 加上五度乘 t, 减去十度乘 t, 那 就是四十五度减去五度乘 t。 来,我们再看角 n o d, n o d 其实就特别好看,因为 o d 不 动,我们只需要用这个图就好了。最开始的时候,在这 这个角度是一个十度乘 t, 我 们刚才第二个就分析了,那 n o d 就 这个九十减去十度乘 t 叫 n o d, 就 等于九十减去十度乘 t。 好, 最后的问题问我们的是,这个角度和这个角度有什么样的数量关系?两倍,哎,对了,就是两倍关系,对吧?所以这个答案就出来了, 角 n o d 就 等于两倍的角 m o c。 像是这种动角问题啊,其实是我们期末的常考题,必考题,我们在分析这种动角问题的时候,你要注意 他的类型是,哎,在问我们这个角度和这个角度啊,他们两个之间的一些关系,是吧?那你要你要注意,你分类讨论的关键在于你要去聊构成这个角和这个角, 他们最关键的元素是射线,你要去聊每一条射线的运动状态,那么我们其实是根据射线的位置关系去分分类讨论的,把这个东西聊透,然后我们用含 t 的 式子去表示它所转动的度数, 就可以去求出来我们题目中问的这些角度关系。所以这种题其实不难啊,他只是有一些麻烦,同学们平时在做题的时候认真一点,你可以的,没问题,难题压轴不用处,曲老师带你有思路。
1065屈笑圆周率 03:37查看AI文稿AI文稿
03:37查看AI文稿AI文稿初一期末考试必考的动脚问题啊,有很多看起来很难,但实际上是忽悠人的,那么今天呢,我们来看一下其中的这个三角板旋转问题怎么解决?三步法哈,动线位置先列时间坐标,当然核心点是找到谁在动,怎 怎么动。第二个呢,把这个角度问题啊,化成做叉求绝对值的问题,这样可以规避前后关联的分歧讨论。第三个呢,去解一个简单的方程就可以了。所以这类题呢,我们首先要看题目当中怎么样去套用我们这个三步法来看问题啊,周围有一个直角三角板啊,它的直角边呢, o m, 在 这个直线上做一射线 o c, 给你个角度啊, b o c 等于一百二十五,也就是说在这个图当中,这个角是一百二十五度,这个三角板开始旋转啊,以每秒七度的这个速度呢,逆时针旋转,也就是说呢,我们整个这个直角三角形啊,它要往左去逐渐的旋转啊,那你旋转到什么时候的时候,这个 o c 恰好是 a o m 的 平分线,我们可以发现啊,这个 a o m 呢,其实它是在不断的运动的,对吧?因为你在没有旋转的时候,这个 a o m, 它实际上是一个平角,也就是一百八十度, 随着往左旋转的进行呢,你会发现这个 m 呢,跑到上面去了啊,那么它的角呢,会越来越小,所以我们这里边要分析的这个动的线啊,实际上是这个射线 o m, 其他的这个直角三角形的这个 n 点啊之类的,跟我们其实没有任何关系啊,我们只找我们想要的那个动线。第一步啊,写动线位置,时间坐标,现在呢,假设啊, o b 啊,这样一个直线向右的方向,它是零度角,那么显然越往左啊,它的角度呢,会越来越大,所以我们可以写 o m, 现在的位置是起点的零度 加上,因为你越转越大嘛,对吧?所以是加号,加上它的速度乘以时间,也就是说七 t 零加七 t 啊,这就是 o m 的 位置, o a 的 位置是固定的,对不对?哎,是一百八十度, o c 的 位置呢,当然也是一个固定的,人家给你了是一百二十五度, 所以现在我们求哎,当 t 等于多少的时候,这个 o c 是 m o a 啊,这个角的平分线,那么这个里边呢,我们可以用到一个平分线的一个公式啊,其实呢,啊,我们就特别类似于这两个点,去找一个 中间点,这样一个概念,当 o c 是 平分线的时候,那么 o c 这个位置实际上是这两条线位置之和除以二,这就是求平均值吧,所以我们来列一百二十五度,它等于 o m 啊,七 t 加上 o a 一 百八除以二,这样就可以了啊,其实非常简单,来,我们快速解一下,把二挪过来,相当于二百五等于七, t 加一百八,对吧,那么七 t 等于七,十 t 等于十。那么这个题呢,有些同学可能会觉得,哎,老师啊,你是不是说的有点复杂啊,完全没有必要啊,因为这个题的旋转特别简单啊,你直接去找哎, 这个,首先你去求 a o c 啊,这个角呢,它等于一百八减一百二十五等于五十五度,对吧?那么你去求哎, a o m 等于一百一十度的时候,这样就可以了,这是完全没有问题的。但是呢,其实假如说我们用这种算术的办法,它并不是通法,假设有的题目射线变得更复杂更多,怎么办? 那么我今天给大家这个方法呢,实际上是三步走,解决所有动角问题的一个通法,那么大家不管是简单题还是难题,只要套用的这个方法,都可以轻松的去解决。总结一下,第一步我们列动线的位置跟时间有关,对吧?速度乘时间加上起点。第二个 把角度问题呢画成做叉,或者说哎平分线这样的一个式子。第三个呢,去解方程就可以了。
148清华史大爷数学思维 13:24查看AI文稿AI文稿
13:24查看AI文稿AI文稿来看题,这是一道动角问题,我们要抓住两点,第一个呢是建立坐标轴,第二个呢,根据实际情况进行分类讨论。好,咱们先看第一题 啊,两个小三角板,一个呢,长一点的啊,我们生活经验知道,短一点的啊, o d, c 啊,这个短一点的 逆时针啊,十五度,当 o d 和 o m, 那 就是要经过一百八十度以后,时间停止啊。问, t 等于两秒的时候会怎么样?好,我们先看第一问, 先建立坐标轴,以 o b 为圆点, o b 为初矢位置, 即零摄氏度,顺时针呢,为正方向。好,所以呢,我们把不动的先找出来。 o b 呢,是不动的啊,已经说过了啊,继续的 o a 呢,也不动,它是三十度。 好,我们再看 o c, o d, 它是要动,动的话就是往左边动,所以呢,咱们就看 o c 真实位置, 这个度数啊,很容易算出来,一百三十五度往左边走,所以呢,减去一个十五度 t, 好,我们再看海水洞, o d 也洞,它是从一百八十度开始,然后呢,减去十五度 t, 啊,所以呢,我们可以算出来,一等于二,那减去三十度,还剩一百零五度,这个减去三十度,还剩一百五十度。 好,那咱们就开始进行搭配, boc 是 哪个角? o b 和 o c 那 么大的减小的,一百零五度减零度。 ok, 搞定一个再继续看, a o d, o a, o d。 好, 大减小一百五十度,减去三十度,就等于一百二十度。好,我们继续 a o c, o a o c 啊,又是大减小。 好,就等于七十五度。好,我们填上去一百零五度, a o d, 一 百二十度, a o c, 七十五度,这里稍微严谨一点,它已经写了一个圈圈。 好,我们继续看第二个想问, 如图二,两个方向盘开始旋转,然后呢? o、 o b 顺着转啊,还记着刚刚开始的这个 o d、 c, 它是逆时针转的啊,所以呢,我们把它们的轨迹也表示出来。 一开始的时候啊,有一个 o b 本来好好在零度,然后呢往右边,那就是二十度 t, o a 呢?从三十度出发,也是加上一个二十度的 t, 还有 o c、 o d, 好, o c, 我 们还记得一百三十五度减去一个十五度 t, o d, 那 就是一百八十度减去十五度 t, 好, 还有一个 o n 是 我们固定的, 一百八十度 o m 也是固定的,那咱们就看第一种情况,它需要 o a 和 o n 重合,也就是说 o a 和 o n 重合,那咱们就 计算一下,重合的时候呢,等于一百八十度 t 呢,就等于七点五,也就是说七点五秒的时候,他们终于停止运动,因为这个时候重合了。好,所以咱们看第一问, 看第一问,他的要求呢是什么? o a、 o d 重合,好,我们看 o a、 o d, 那 这个时候呢? o a、 o d 重合,我们看发生什么事情,两根线变成一根线,位置在同一个位置 啊,就这个题我们解一下, t 呢,可以算出来啊,三十五,一百五,那就是一百五十度,除以三十五度,给它画个减起三十秒。 好,有了这个时间,哎,我们发现没有,最大时间七点五秒,然后这个呢是四秒多一点点啊,那咱们看它的已知条件, a、 o d 表示一下 a、 o d, 看咱们知不知道大减小 o d, o a, 好, 那咱们不知道,直接把它给写下来, 三十度加上二十度的 t 减去一百八十度减去十五度的 t, 好, 这个时候呢,咱们把它写下来, 就等于一百五十度减去三十五度的 t。 好, 这个时候我们想一想看,之前我们是有一个已知条件的 t 呢,是在七分之三十秒以内,咱们带进去啊,正好呢,这个是一个正数,所以直接把符号给去掉了啊,这是 a、 o d, 那 咱们再看 b、 o c, 找到 o b 和 o c, 哎,你是 o b, 你 是 o c, 继续做个减法,它呢来一下,那就是三十五度的 t 减去一百三十五度, 那么这个呢,我们还是这个有可能是正数,有可能是负数,所以的话,我们现在只能是保留这个绝对值符号,那么我们就得到 已知条件, a、 o、 d 呢,是它的一点五倍,所以呢,一百五十度减去三十五度的 t, 它就等于一点五倍的 三十五度的 t 减去一百三十五度。好,那咱们解方程第一种情况,这个呢,要是正数, 我们让三十五度的 t 大 于一百三十五度 g, t 大 于。 好,那这个时候呢,我们解方程解出来一百五十度减去三十五度的 t, 就 等于一点五倍的三十五度的 t 减去一百三十五。那咱们解方程解出来是多少呢 啊? t 就 等于三十五分之一百四十一啊,咱们也确认一下,哎,正好是比它大啊,所以做的挺好的。那咱们再看第二问, 当三十五度 t 小 于一百三十五度时啊,这个时候呢,咱们得变个号,加等于号, 需要呢,一百五十度减三十五度的 t, 就 等于一点五倍的 一百三十五度减去三十五度的 t, 这是编号,所以呢,我们就得到新的 t, 三啊,这个三就是三分三十五分之一百零五啊,是比它小的,所以呢,两个都对。 中上所述 t 等于 或三。好,那咱们再看最后一问, 第二问呢,应用绝对值说,我们要分类讨论好。第一种情况,当 a o d 减去 b o c 啊,它就是五度, 那这个时候呢,咱们就把上面的移值条件放进去, a o d 呢,已经是一百五十度减去三十五度的 t, 而 b o c 呢,咱们确实不知道,所以呢,还是要保留绝对值, 它们等于五度。再分类讨论,当这个是一个正数的时候, 解方程减去。 好,这个时候你发现减三十五加三十五, t 直接抵消了,最后呢,十五等于五,方程不成立。 继续, t 大 于等于三十五分之一百三十五式,再来一个新的方程, 这个时候呢,其实就是绝对是变号了,等于五度解出来呢, t 等于四,哎,挺好,因为它就是三十五分之一百四,比它正好大一点点。继续咱们看第二种情况, 当 b o c 减去 a o d 等于五摄氏度啊,五度,这个时候呢,我们又得到个新的方程,那就是一百三十五 减去三十五度, t 减去打括号,就是减号,前后交换顺序等于五度啊,还是一样的。当 t 小 于, 这个时候呢啊,放成不成立, 那咱们看下一种情况,当 t 大 于, 这个时候呢,我们就要变个号减去。 好,然后咱们解方程, t 就 等于呢七分之二十九,那咱们比对一下,乘以三十五 五啊,一百五比他要大一点点,正好,所以呢,这个是对的。然后呢这个也是对的,所以我们直接在书上写一下 t 呢,等于四秒 或七分之二十九。好,这个题我们讲完了,下个视频我们再见。
53菁菁学爸 48:43查看AI文稿AI文稿
48:43查看AI文稿AI文稿作为七上数学的终极大 boss, 动脚问题排第二,没人敢说第一。题型多变不说,一会儿是射线旋转,一会儿是角平分线叠加。最让人头疼的就是藏在里面的分类讨论,稍不留意就会漏解,就算思路对了,最后还是拿不到满分。 很多同学都问我,有没有一招先的通用解法能搞定所有动脚问题? sorry, 这还真没有。但是别慌,我们学习数学讲究的就是一个万变不离其宗,不管题型的核心逻辑都是相通的。 所以本节课汤姆老师将会用一个视频,五道经典例题,循序渐进,有浅入深,带你彻底搞懂动脚问题。如果对你有帮助,记得艾特一下你的学渣同学也来听一听。对了,千万不要忘了一键三连哦!搬好小板凳开课! 所谓动角,简单说就是大小会发生变化的角,它和我们之前学的固定角是相对的概念。举个直观的例子,已知点 o 在 直线 a、 c 上,射线 o b 绕点 o 从 oc 位置开始,以每秒十度的速度逆时针旋转。 旋转前,角 b o、 c 等于零度旋转三秒后,角 b、 o、 c 等于十乘以三等于三十度。旋转十秒后,角 b、 o、 c 等于十乘以十等于一百度。那旋转 t 一 秒后呢?显然角 b、 o、 c 就 变成了十乘以 t, 我 们就用十 t 来表示。 可以看到,这个角 b、 o、 c 是 随着 ob 的 旋转而不断变化的,所以角 b、 o、 c 就 属于动角。 同理,角 a、 o、 b 也是动角,它可以表示为一百八十度减十 t。 这里有一个非常容易出错的点,需要同学们格外注意。上面我们说到,在射线 o、 b 旋转的过程中,动角 b、 o c 等于十 t, 对 吧? 那是不是无论 o b 旋转多少角度,都可以用这个表达式来表示角 b、 o c 呢? 当然不是,我们来看图,当射线 o b 从 oc 位置旋转到这个位置的时候,他转过的角度已经超过了一百八十度。此时我们说角 b、 o c 的 时候就容易有歧义, 到底是说这个角还是说这个角呢?就不太能分清了。为了规避这个问题,我们就规定在初中阶段研究的所有角度都是小于等于一百八十度的。 所以当射线 ob 转过的角度超过了一百八十度时,我们说的角 boc 就 表示的是下面这个角, 它是满足在零到一百八十度之间这个要求的。而此时角 boc 如果用 t 表示的话,就变成了三百六十度减去射线 ob 转过的角度十乘 t, 即三百六十度减十 t, 并且这时的角 aob 我 们也知道了,等于一百八十度减角 boc, 即十 t 减去一百八十度。 我们可以总结一下,对于上述动角问题来说,当 o b 的 旋转角度大于等于零度,并且小于等于一百八十度的时候,角 b o c 等于时辰 t。 角 a o b 等于一百八十度减去时辰 t。 而当 o b 的 旋转角度大于一百八十度,小于等于三百六十度的时候,角 b、 o c 则等于三百六十度减去时辰 t。 角 a o b 等于十乘以 t 减去一百八十度。 ok, 以上就是射线运动过程中动角的表示形式,我们来做两道基础的动角题型应用一下。先看第一题,他说 o 点在直线 a c 上,角 a o d 等于三十度, 这个角是三十度角。射线 o b 从 o d 出发,以每秒十度的速度逆时针转动, 有一条射箭 o b 从 o d 出发,是逆时针旋转,速度呢,是每秒十度。我们来标注一下, o b 是 从 o d 的 位置出发,逆时针转动速度 v 等于十度,每秒问多少秒后角 a o b 等于九十度。那首先我们来简单的模拟一下 o b 的 运动状态, o b 是 从 o d 的 位置逆时针转动,假设它转动到这个位置, 那根据刚才我们对于这个动角表达形式的描述,它转动的角度就应该是十 t 吧,每秒转动十度,那 t 秒就转动十 t。 看此时角 aob 就是 这个角, 那现在要让角 aob 等于九十度,所以这个 ob 呢,它就应该转动到这个位置。我们来算一下这个角 aob, 它是可以写成这个角 a o d 加上角 b o d 的 吧。于是我们就得到了这个三十度,加上十 t, 它是等于九十度的啊。这个角 b o d, 它转动的角度可以用十 t 来表示,这里是三十度,所以就得到了这个等式。那解出来这个 t 呢,它就等于六秒。那这道题结束了吗?哎,当然没有啊,它还有第二种情况,同学们看, 当这个 o b 它继续转转转,转动到这个位置,那么此时角 a o b 是 不是又变成了九十度啊?所以第二种情况下呢, 就是这个 o b 继续转转到了刚才的反向延长线上。为了区别一下,我们把这个叫做 b 撇,此时这个角 a o b 撇,是不是也满足等于九十度啊, 那这个时间 t 呢?也非常好求,我们只要在刚才的基础上继续转动一百八十度即可把刚才这个记作第一种情况,那么第二种情况下呢?那么这个十 t 就 等于一百八十度, 那为了区别一下,我们把它叫做 t 撇吧,算出来这个 t 撇等于十八秒,也就是说 o b 在 原来的基础上继续转动一百八十度,那需要的时间是十八秒,再加上刚才的六秒,此时的这个 t 呢,就等于 六加十八等于二十四秒。所以这道题一共有两个答案, t 等于六秒的时候和 t 等于二十四秒的时候,这个角 aob 都可以满足等于九十度。 第二题他说木条 abc 定在一起,角一等于一百二十度,角二等于五十度。木条 a 以每秒四度的速度绕着 a 点顺时针旋转一周, 这个木条绕着这个旋转点 a 顺时针旋转一周。求当木条 ab 垂直的时候, 旋转时间为多少秒。那这道题的题干呢?也很清楚,小 a 绕着这个 a 点顺时针转动,那要解决这个问题的话,我们先把它的垂直状态下的图像给他画出来。同学们看,这个木条 a 从原来的状态转动到这个位置,因为垂直,那这个角呢, 实际上是一个直角吧,这个木条 a 转动的角度就应该是这个角,它的速度是四度,每秒时间呢,可以设为 t, 所以 它的旋转角就应该是四 t。 那 接下来我们来看看这个角度能不能求,如果能求的话,这个时间 t 不 就出来了吗?怎么来求这个角呢?这里是一个平角吧, 也就是一百八十度,所以假设我们能够把这个角度算出来,用一百八十度减去它,是不是就得到了这个木条 a 的 旋转角啊?哎,这是一个思路,我们可以把这个角记作角三,那这个角三怎么求呢?好,我们来看这个已知条件,角一等于一百二十度, 所以这个角是不是也是一百二十度啊?因为他俩是对顶角,对顶角相等,我们又知道角二等于五十度, 这里又是一个直角,所以角二和这个小角是互余的吧。我们把这个小角记为角四,于是就得到了这个角二,加上角四,它是等于九十度的。那我们又知道角二是等于五十度,所以就能得到角四等于四十度, 角四等于四十度。刚才又说这个大角它是等于角一等于一百二十度的,所以也就得到了这个角三,它就应该等于一百二十度,减去四十度,那就等于八十度,角三等于八十度,那我们刚才这个旋转角不就等于一百度吗? 哎,所以这样我们就得到了原来这个旋转角四 t, 它是等于一百八十度,减去八十度等于一百度, 算出这个 t 呢,它就是二十五秒,所以当 t 旋转二十五秒的时候,就能够满足这个木条小 a 和小 b 垂直吧。 那么继续看还有没有其他情况呀?当然有啊,同学们看,当这个木条 a 在 这一种状态下,它继续旋转,转转转一百八十度,是不是又能跟这个木条小 b 垂直啊?为了方便同学们的理解,我们可以把这个木条转呢看成一条 射线的转动,我用这个颜色来表示,那这是第一种情况,那第二种情况下呢?哎,这根木条他转到了这个位置,同学们看, 在这种状态下,这个木条 a 依然和这个木条 b 是 垂直的吧。所以这道题和我们刚才那个第一题呢,是非常像的啊。我们把 这个叫做第一种情况,那第二种情况呢,就是这个小木条他在转动一百八十度,那他的旋转角依然可以用四 t 来表示啊,也就是四 t 等于一百八十度, 算出这个 t 他 是等于四十五秒,我们把这里叫做 t 撇, t 撇等于四十五秒, 也就是说,在原来的基础上,他继续转动四十五秒,又能得到 ab 两个木条垂直。所以第二种情况下,这个时间 t 他 就等于二十五,加上四十五也就等于七十秒。 所以这道题呢,也是有两个答案, t 等于二十五秒和 t 等于七十秒,都能够满足木条 ab 垂直。 这两道题做完,是不是感觉貌似动脚问题也不是很难吧?别高兴太早,要是真这么简单,人家就不是大 boss 了。接下来咱们加点难度,再引入一个知识点,角平分线 还是看前面的问题,他说在射线 o d 始终平分角 b o c, 然后让我们求角 b o d 的 大小,这时候又该如何处理呢?我们一起来分析。显然还是需要分两种情况。第一种情况,当 o b 旋转的角度大于等于零度,小于等于一百八十度时, 因为角 b、 o c 等于十 t, 根据角平分线的性质,角 b o d 等于二分之一倍的角 b o c, 即二分之一乘以十 t, 最终等于五 t。 第二种情况,当 ob 旋转的角度大于等于一百八十度,小于等于三百六十度时, 因为角 b、 o、 c 等于三百六十度减十 t。 根据角平分线的性质,角 b、 o、 d 等于二分之一倍的角 b、 o、 c 即二分之一,乘以括号,三百六十度减十 t, 最终等于一百八十度减五 t。 我 们再看两道包含角平分线的动角问题,难度比前两题大了不少,千万别分心。点 o 是 射箭 o b 上的一点 点, p 是 射线 o a 上的一点角 b、 o、 c 等于一百度,所以这个角就是一百度。射线 op 绕点 o 以每秒十度的速度逆时针旋转一周,这个射线 op 是 绕着 o 点逆时针旋转的啊,速度呢,是十度每秒 o d。 平分角 b o p 旋转时间即为 t 秒。啥意思呢?我们来简单说明一下。比如说,当这个 o p 转到这个位置,那 o d 作为这个角 b、 o p 的 平分线差不多就在这个位置。 先来看第一个小问题,当 o p 恰好为射线 o c 的 反向延长线时,求时间 t 等于多少?那我们知道 o c 在 这里,它的反向延长线 就是这条线,那 o p 转到这个位置的情况下,让我们求这个时间 t。 这个第一小段还是比较简单的啊。 o p 的 转动速度我们已经知道了,它是十度每秒, 旋转的时间即为 t 秒,旋转的角度就是十 t。 那 当它转到 o c 的 反向延长线上时,显然这个角和这个角是相等的吧。此时这个十 t 呢,它就是一百度 t, 解出来也就是十秒,所以这个第一空就是十秒。再来看第二个问题,若角 cop 等于角 p o d 的 时候,让我们求时间 t, 那 么这个第二问呢,是需要进行分类讨论的啊。我们先简单的分析一下这个 op 的 运动状态,同学们看 op 的 位置它是不停的在变化的吧,所以这个角 cop 呢,它的角度也是在变化, 比如说当 o p 它就转到这个位置的情况下,那么角 cop 就是 这个角,那这个角度呢,它就可以写成这个八十度加上十 t 吧,那此时角 p o d, 它就是这个角,也是可以用含 t 的 表达式写出来的。但是请大家注意了, 随着这个 o p 不 断的旋转旋转,当它转到这个位置,再往后的话,这个 cop 它就变成了这个角了吧,我们刚才用八十度加上十 t 的 这个表达式就不成立了啊,所以接下来这个位置就是我们分类讨论的临界点, 那我们知道这个角是一百度,刚才第一问我们已经知道了, o p 转到这个位置的时候呢,是需要十秒的吧,所以第一种分类的情况也就确定了,当这个 t 大 于零, 小于等于十秒,在这种情况下,我们来看一下是否能找到满足这个条件的时间 t。 为了方便大家的理解,我们重新画一个图啊,同学们看,那此时角 cop 就是 这个角度,角 p o d 呢,就是这个角度。哎,显然这两个角看起来是有可能相等的吧。那接下来呢,我们就用含 t 的 表达式,分别把这俩角都写出来,角 c o p, 显然它是可以写成角 a o c 加上角 a o p 的 吧,也就等于八十度加上十 t, 对 吧?刚才我们说这个 o p 的 速度是十度每秒的运动时间 t, 所以 这个角度就可以写成十 t 啊。 这样的话,我们就把角 cop 给它写出来了。再看角 p o d, 角 p o d, 在 这里 我们又知道 o d 是 这个角的角平分线,所以这个角 p o d, 它是等于二分之一倍的角 p o b, 那 p o b 又可以写成这个一百八十度减去角 a o p 吧,这样的话,这个角 p o d 也就能写出来了啊。角 p o d, 它是等于 二分之一倍的角 p o b, 那 角 p o b 又可以写成一百八十度减去角 a o p, 也就是一百八十度减去 十 t。 那 整理一下这俩等式,就能得到这个角 p o d, 它是等于九十度减去五 t, 这样我们就把这个角 p o d 也用很小 t 的 表达式写出来了。那最后因为这俩角相等,也就能够得到 八十度加上十 t 等于九十度减去五 t, 那 解出来这个 t 呢?等于 三分之二秒。好,那这个三分之二呢?确实在零到十秒这个范围内。接下来的情况呢?前面我们已经讲了,当这个 o p 转到这个位置的情况下,继续往后转, 这个角 cop 的 表达式就需要变化了吧,那大概这个 o p 转到这个位置 o d 呢?大概在这个位置, 那此时角 cop 和角 p o d 也可能出现相等的情况吧。这里必须要提醒一下这个中间态,同学们一定要自己动手去画一下,这个是我们解决分类讨论非常重要的一个能力,一定要学会自己动手画图, 同学们看,在这种情况下,这个角 cop 和这个角 p o d 是 不是也有可能出现相等的情况下啊?那这个就是第二种情况啊。当 t 大于十秒,小于等于三十六秒,此时角 cop 又该怎么表示呢?这个角 cop, 它是可以写成角 boc 减去角 bop 吧,那这个角 bop 呢?又可以写成这个大角减去一百八十度, 对不对?因为我们这个 o p, 它是从这个位置出发,一直旋转到了这个位置啊。 ok, 那 这样我们就可以先写一下角 p o b, 它是等于十 t 减去一百八十度,看,十 t 就是 这个角度,那减去这个平角一百八十度,是不是就是角 p o b 的 度数啊?角 c o p 呢?又可以写成角 b o c 减去这个角 p o b, 那这样我们就得到了角 cop, 它是等于角 cop 减去角 pob, 整理一下这个表达式就得到了。这个角 cop, 它是等于二百八十度减去实体, 这个 cop 的 表达式已经有了。那再来看这个角 p o d, 那 p o d 就 简单了,因为 o d 始终平分角 p o b, 所以 p o d 就 等于这个角的二分之一啊。 角 p o d, 它是等于二分之一倍的角 p o b, 整理一下,也就是五 t 减去九十度, 这样角 p o d 的 表达式也有了。那最终因为这俩角相等,所以二百八十度减去十 t, 就 等于五 t 减去九十度, 解出来这个小 t 呢,它是等于三分之七十四秒。最终这道题的答案呢,就是 t 等于三分之二和 t 等于三分之七十四秒。这两种情况下,哎,都是符合要求的啊, 这道题我们就给他说清楚了,同学们一定要记得自己在做题的时候,一定要动手去画一下这个中间态,那有同学说,这个 o p 在 这个位置的时候,或者说在这个位置的时候可不可以啊?哎,你要自己动手去画一下, 除了这两种情况下,在其他位置的时候,都没办法能找到满足条件的这两个角。 第四题,他说 o 点是直线, ab 上的一点角 c o d 是 直角,所以这里是一个九十度的角, o e 平分钝角 b, o c 是 这个钝角的角,平分线 角 a o c 等于三十度角 c o d 绕着 o 点以每秒五度逆时针旋转, t 秒 t 的 范围呢,是在零到三十六度。同学们看这道题和我们前面讲的那个题型呢,稍有不同, 他讲的是这个直角绕着这个 o 点开始逆时针旋转吧,我们前面讲的都是射线绕着某一点旋转。问,在旋转的过程当中,角 a、 o c 和角 d、 o e 之间的数量关系,这个角 和这个角之间的数量关系。那有了前三题的铺垫,我相信大多数同学在做这道题的时候,应该会有一个大概的思路,要想探究这两个角之间的数量关系,肯定是要用含 t 的 表达式 把这两个角都给他表示出来,因为这个角度他都是在变化的啊。那么具体应该怎么表示呢?下面我们一起来分析一下。首先题干当中给到的是这个角绕着 o 点,然后每秒五度逆时针旋转, 那显然角度旋转这个过程是比较抽象的吧,我们要把它变成我们熟悉的形式, 所以对于这个条件,我们可以把它转化成 o c 和 o d 这两条射线的旋转,所以射线 o c 旋转的速度 v c, 它就是五度每秒,射线 o d 旋转的速度也是五度每秒,那方向呢?都是逆时针啊, 这是第一个细节,同学们需要注意的。再来看第二个细节,他说这个旋转的时间 t 是 在零到三十六度吧,这个条件又有什么用呢? 同学们看 oc 的 速度是每秒五度,所以旋转三十六秒。那么显然这个 oc 呢,它的最大旋转角度就是 一百八十度,相当于告诉我们射线 o c 转到这个位置以后就停止,那同理,射线 o d 最大的旋转角度也是一百八十度。 那接下来我们就来看看具体的在旋转的过程当中,这个角 a o c 和角 d o e 大 概是如何变化的啊?那这里又需要同学们去模拟一下这两条射线运动的中间状态。 比如说我们看射线 o c, 假如它运动到这个位置,那 o d 始终跟它垂直,所以 o d 大 概在这里,这个角还是九十度,那 o e 呢?同学们看 o e 是 角 b o c 的 角平分线, 并且这个角 b o c, 它始终是一个钝角吧,所以 o e 大 致应该在这个位置,这个细节非常关键。同学们看角 c o e 大 致应该在这个位置。这个细节非常关键。同学们看角 c o e 大 致应该在这个位置。这个细节非常关键。同学们看角 c o e, 所以它的角度一定是小于九十度的,那 o d 是 和 o c 垂直的,所以 o e 大 概就在这个位置啊,在 o d 的 左边,那此时角 a o c, 它就应该是这个角,它的旋转角度呢, 可以用五 t 来表示吧,旋转的速度是五度,每秒时间 t, 所以 旋转的角度就是五 t, 那角 d o e 呢?就是这个角,这个角度呢,也是可以用含 t 的 表达式来写的吧。同学们看,我们可以写成九十度减去这个角 c o e, 因为这个 c o e 是 等于 c o b 的 一半,那 c o b 是 可以写成一百八十度减去角 a o c 吧。那通过刚才的分析,我们知道这俩角都是可以用含 t 的 表达式来写的吧,这样我们就完成了第一阶段的分析。那接下来同学们继续看, 当这个 o c 继续旋转,一直到它转到 o a 的 这个位置,再往后转的话, 比如说 o c 转到了这个位置,现在角 a o c 就是 这个角度了吧,那这个角度它就不再是这个三十度减去五 t, 而是五 t 减去三十度了吧。也就是说这个 o a 就是 oc 在 旋转过程当中的临界状态,只要突破 oc 的 位置,再往后这个角 a o c 的 表达式就要发生变化了。我们再来看一下 o d, 那 o d 呢?它就跑到这个位置, 那此时角 b o c 就 变成了这个角,所以 o e 的 位置大概在这里,显然这个角 d o e 的 表达形式也发生了变化吧。 那经过刚才的这个分析呢,我们基本上就已经找到了接下来分类讨论的标准。同学们看,当 o c 从这个位置转到这个位置转动了,是三十度,他的速度呢,是每秒五度,所以他转到这个位置需要的是六秒。 所以这道题的第一种情况就应该是当时间 t 大 于零,小于等于六秒的时候,此时角 a、 o c, 它是等于三十度减去 五 t。 同学们看角 a、 o c 是 不是等于这个三十度减去它的旋转角度啊?那这样我们就有了角 a、 o c 的 表达式。再看角 d、 o e, 我 把这里面多余的两条线段先给它擦掉啊。同学们看, 此时角 d、 o e 应该是这个角,那这个角呢?前面我们说了,可以写成这个直角减去角 c、 o e 吧。具体我们来写一下啊。 角 d o e, 它是等于九十度减去角 c o e。 我 们又知道 o e, 它是角 c o b 的 角平分线, 所以角 c o e, 它是等于二分之一倍的角 c o b。 也就等于二分之一倍的一百八十度减去角 aoc。 角 c o b, 它可以写成这个一百八十度减去角 a、 o c。 化简一下,它就变成了九十度减去二分之一倍的角 a o c。 那 角 a o c 又等于三十度减五 t, 所以 它就等于七十五度加二分之五倍的小 t, 对吧?因为角 a、 o c 是 等于三十度减五 t, 那 二分之一倍的角 a、 o c 就是 十五度减去二分之五 t, 那 九十度减去这个角,整理一下,它就变成了七十五度加二分之五 t。 有 了角 c、 o e 的 表达式,那这样我们就能得到这个角 d o e, 它就等于十五度减去 二分之五倍的小 t。 现在同学们再来观察,角 a、 o c 是 等于三十度减五 t, 角 d o e 是 等于十五度减二分之五 t。 显然在这种情况下,我们就得到了角 a o c, 它是等于两倍的角 d o e。 那 接下来我们再来看第二种情况,那第二种情况呢?就应该是当 t 大 于六秒,小于三十六秒的情况啊。我们先把这个草图先画出来,同学们看, 此时角 a o c 就是 这个角度,那这个角呢?我们就可以用这个大角减去三十度吧。那这个大角其实就是射线 o c 的 旋转角,也就是五 t, 所以 角 a o c, 它就是五 t, 减去三十度。再看角 d o e, d o e 就是 这个角。 那这个角呢?我们可以看成两部分,可以写成这个九十度,加上角 coe 吧。这里我们写一下角 d o e, 它就等于九十度, 加上角 c o e c o e 是 这个角。因为 o e 是 角 b o c 的 角平分线,所以角 c o e, 它是等于二分之一倍的角 c o b。 那 c o b 又可以写成 一百八十度,减去这个角 aoc, 所以 它就是二分之一倍的括号。一百八十度减去角 aoc, aoc 的 表达式我们已经写出来了,只要把它带进去啊, c o e 的 表达式就有了,那 c o e 的 表达式有了角 d o e 也就能写了。整理一下这个角 d o e, 它就等于一百九十五度,减去 二分之五倍的小 t, 我 们再来对比一下这两个角。角 a o c 是 五 t 减三十度,角 d o e 是 一百九十五度,减二分之五 t。 对 比一下这两个表达式的形式, 我们就能得到角 a o c 加上二倍的角 d o e, 它是等于三百六十度的啊。 同学们看,我们把它扩大两倍,它就变成了三百九十度,减去五 t, 它俩一相加是不是就等于三百六十度啊?那第二种情况下,这俩角的数量关系呢?就应该是角 a、 o c 加上二倍的角 d、 o e 等于三百六十度。 这道题我们就说清楚了啊,同学们注意消化一下我们刚才对于整个细节的分析啊,因为这道题当中的 o d、 o c、 o e 都是在变化的, 那解析的核心呢,就是要找到这个 o c 旋转过程当中的临界状态。因为临界状态一旦确定,那么我们就可以用含 t 的 表达式,把这里的动角 a、 o c 和动角 d、 o e 的 形式都给它写出来。 通过前面四道题的训练,我相信大多数同学对于动角问题的处理方法一定有一些思路了。接下来继续提高难度,把前面引入的角平分线换成角的等分线, 比如还是前面的问题。不过在射线 o b 旋转的过程中,射线 o d 变成了角 b、 o c 的 四等分线,这时候角 b、 o d 的 大小又等于多少了呢? 首先同学们要明确, o d 是 角 b、 o c 的 四等分线,其实对应的有两种情况,一种是 o d 更靠近 o b 边,另一种是 o d 更靠近 o c 边。 再结合, o b 旋转的角度大于一百八十度和小于一百八十度,也需要分两种情况。所以我们分析角 b、 o d 的 大小时,就需要分四种情况来讨论。首先,当 o b 的 旋转角度时,就需要分四种情况来讨论。首先,当 o b、 o d 的 大小时,就需要分四种情况来讨论。首先,当 o b、 o c 等于十 t, 如果此时 o d 是 更加靠近 o b 边的四个分线,则角 b、 o d 比上角 c、 o d 等于一比三,所以角 b、 o d 等于四分之一倍的角 b、 o c 也就等于二点五 t。 而如果 o d 更加靠近 o c 边,则角 b、 o d 比上角 c、 o d 等于三比一, 所以角 b、 o d 等于四分之三倍的角 b、 o c 也就等于七点五 t。 其次,如果 o b 旋转角度在一百八十度到三百六十度之间,角 b、 o c 等于三百六十度减十 t, 那 么当 o d 更靠近 o b 时,角 b、 o d 就 等于四分之一倍的角 b、 o c 也就等于九十度,减去二点五 t。 相反, o d 更加靠近 o c 时,角 b、 o d 就 等于四分之三倍的角 b、 o c 也就等于九十度,减去七点五 t。 ok, 这就是含有角的等分线的动角问题。很显然,一旦引入等分线,需要我们考虑的情况就会明显增加,难度也就一起提升了,大家一定要注意做好分类讨论。最后,再来看一道涉及等分线的例题, 这道题一共有三个小问,我们分别来看一下。先看这个第一问,他说,如图,角 aob 等于四十度,若角 aoc 等于三分之一倍的角 boc, 求角 boc 的 度数。面对这样的问题,同学们一定要自己动手去画一下。那这里呢?实际上是有两种情况, 第一种情况就是 o c 在 角 a、 o b 的 内部,这种情况下,角 a、 o c 有 可能是角 b、 o c 的 三分之一吧,那么我们把它设为 x, 那 角 b、 o c 的 大小呢?就是三 x, 相当于这个 o c 就是 角 a、 o b 的 四等分线。那简单的计算一下, x 加上三 x 是 不是等于四十度啊? 所以算出 x 就 等于十度,所以在这种情况下,角 boc, 它就是三十度。那第二种情况呢?哎, o c 还可以去角 aob 的 外面,那也有可能存在角 aoc 等于三分之一倍的角 boc 吧,这个角 它是这个角的三分之一,所以我们把它设为 x, 所以 这个角 aob, 它就应该是二 x。 那 么在第二种情况下呢,我们就得到了二 x 等于四十度,所以 x 是 等于二十度,角 boc 它就等于六十度。所以这个第一小问呢,有两个答案, 三十度,六十度,都是符合要求的。下面我们再来看一下第二小问呢,有两个答案,三十度,六十度都是符合要求的。下面我们再来看一下第二小问呢。图形看起来比刚才要复杂一点啊,但是难度并没有大多少。 他说角 a o c 等于二十度,这个角是二十度, o m 是 角 a o b 内部的一条直线 o m。 在 这里 o n 是 角 m o c 的 四等分线, 且三倍的角 c o n 等于角 n o m。 哎,这个条线非常重要,我们来看一下什么意思,他说 o n 这条射线呢,是角 m o c 的 四等分线,并且 三倍的角 c o n 等于角 n o m。 根据前面我们对于角的等分线的理解,这里我们把角 c o n 设为 x, 那 角 n o m, 它就是三 x。 求四倍的角 a o n 加上角 c o m 的 大小。好,我们来看一下,角 a o n 呢,是这个角,那这个角,显然它是可以写成 a o c 减去角 c o n 吧。 角 a o n, 它是等于角 a o c 减去角 c o n, 也就是二十度。减去 x。 我 们再来看一下这个角 c o m。 那 角 c o m 指的是这个大角,那这个角它不就是这个角,加上这个角,也就是四 x 吧。所以这个角 c o m, 它就等于角 c o n 加上角 m o n 等于四 x。 现在我们把这个角 a o n 还有角 c o m 都用含有 x 的 表达式写出来了吧,所以这样我们就得到了四倍的角 a o n 加上角 c o m, 它就是 八十度,减去四 x, 再加四 x, 结果就等于八十度。所以这个第二问,只要同学们理解了四段分线,然后设 x, 把这两个要求的角都给他表示出来,那最终就能算出这两个角的和,哎,他就是一个定值啊,八十度。 接下来我们再来看这道题的第三问,这个第三问还是比较复杂的,因为接下来在解决这个问题的过程当中,我们需要分多种情况进行讨论。他说角 a o c 等于二十度,这个角是二十度。这里说明一下,角 a o b 始终是等于四十度啊。这个是前面题干当中给到的条件, 射线 o m 绕着 o 点,从 ob 开始,以五度每秒的速度逆时针旋转一周,直到 ob 结束。什么意思呢?有一条射线 o m, 它是从 ob 的 位置 逆时针旋转,哎,旋转一周,速度是每秒五度。在旋转的过程当中,射运动的时间为 t o n 是 角 m o c 的 四等分线,且三倍的角 c o n 等于角 n o m。 我 们来理解一下这句话,比如说假设 o m 转到了这个位置, 那角 m o c 就是 这个角,他说 o n 是 角 m o c 的 四等分线,并且三倍的角 c o n 等于角 n o m, 那 o n 大 致就在这个位置,这里就是角 c o n, 这个就是角 n o m。 根据前面我们对于这个角的等分线的理解, o n 这条边肯定是更靠近 o c 的, 对吧?当 t 在 某个时间范围内, 四倍的角 a o n 加上角 b o m 会是一个定值,让我们写出这个定值,并且指出对应的时间 t 的 范围。通过前面几道题的讲解,我相信大多数同学在做这道题的时候,应该会有一个大方向了。要想求出这两个角的和是不是一个定值, 那首先我们需要想办法把这个角 a o n 和角 b o m 都用含 t 的 表达式给它写出来吧。要想写出这两个角的表达式,那我们就得仔细的去分析一下 当这个射线 o m 在 运动的过程当中,这个角 a o n 和角 b o m 的 位置,下面我们一起来分析一下。角 b o m 指的是这个角 o m 的 速度是每秒五度, 经过时间 t, 它的旋转角就应该是五 t 角 a o n 是 这个角,怎么表示这个角呢? o a, 它是一条固定的射线,所以这个角的大小它是由这个射线 o n 决定的吧。 那我们知道,在这个 o m 旋转的过程当中,这个射线 o n 的 位置也会发生变化,因为它始终要保证是这个角 c o m 的 四等分线。 比如说当 o n 在 这个位置的情况下,那这个角呢?我们就可以写成角 a o c。 减去角 c o n, 那 c o n 它又是四分之一倍的角 c o m c o m 又可以用这个六十度减去这个五 t, 所以这个角 a o n 它一定是可以用含 t 的 表达式写出来的吧。但是同学们继续看,随着这个 o m 不 断的旋转,直到这个射线 o m 它旋转的位置突破这一条射线,比如说 c m 转到了这个位置, 同学们看,那现在角 b o m 就是 这个角,这个角依然可以用五 t 来表示吧,但是这个 o n 的 位置就已经发生变化了。 同学们看, m o c 就 变成了这个角,那 o n 作为它的四等分线,还得要保证三倍的角 c o n 等于角 n o m, 那 o n 大 致就跑到了这个位置。在这种情况下,角 a o n 是 不是就变成了这个角了呀?此时这个角的表达式就已经发生了变化吧,它就应该变成这个角加上这个角了。所以我们会发现, 当 o m 旋转的角度大于六十度以后,角 b o m 的 表达式没有发生变化,但是角 a o n 的 表达式已经发生了变化啊。这样的话,我们第一种分类情况其实就已经出来了。那为了后面方便同学们的理解,我们可以把这个 o m 旋转的角度 用字母阿尔法来表示。那第一种情况就应该是,当这个阿尔法角在零到六十度之间, 这个 o m 的 速度是五度每秒,对应的旋转时间就应该是零到十二秒。那接下来我们就来看一下 t 在 这个时间段内,角 a o n 和角 b o m 的 表达式怎么写。 我把这个图重新画一下,看起来有点乱,同学们看,我们可以先把这个角 b o m 写出来,因为它是比较好写的,它的速度是五度每秒,那时间 t 内它转动的角度就是五 t, 角 b o m 就 等于五 t。 再看角 a o n, 那 这个角呢?我们可以写成角 a o c。 减去角 c o n, 那 角 a o c, 我 们是知道的,它是等于二十度。角 c o n 呢,它是等于四分之一倍的角 c o m 吧。角 c o n 等于四分之一倍的角 c o m, 那 角 c o m, 我 们又知道,可以写成六十度,减去五 t, 也就等于四分之一倍的括号,六十度减去五 t。 整理一下这个表达式,我们就能得到,角 a o n, 它是等于五度,加上四分之五 t。 角 b o m 的 表达式有了,角 a o n 的 表达式也有了,所以就能得到 四倍的角 a o n。 加上角 b o m, 它是等于二十度加十 t。 显然在零到十二秒这个范围内,这个四倍的角 a o m 加 角 b o m, 它的值不是一个定值吧。那下面我们再来看第二种情况。这个第二种情况下呢,我们要讨论的就是,当 o m 旋转的角度在六十到一百八十度之间, 那为什么是在六十度到一百八十度之间呢?刚才我们已经说过,当 o m。 旋转的角度突破这个六十度以后,角 a o n 的 表达式就会发生变化吧。当射线 o m。 旋转的角度突破了这个一百八十度,比如说 o m 转到了这个位置, 那么此时角 b o m, 它就是这个角嘞。那这个角的表达式,它就不再是刚才的五 t 了吧。 所以接下来我们讨论的第二种情况呢,这个旋转角阿尔法,它只能在六十到一百八十度以内, 因为在这个时间段内,角 b o m 以及角 a o n, 它们的表达式都是统一的啊。那那个时间 t 呢?我们来算一下,就应该是 大于十二秒,小于等于三十六秒。此时角 b o m, 它的表达式依然是五 t, 因为 om 旋转的速度是五度每秒,那时间 t 内它转动的角度就应该是五 t。 角 a o n 呢, 它就是这个角,那这个角呢?它就可以写成角 a o c 加上角 n o c a o c, a o c 还是二十度。 角 a o b 还是四十度。角 a o n, 它就等于角 a o c 加上角 c o n, 这个角依然是二十度。那么角 c o n, 我 们说它始终是等于四分之一倍的角 m o c, 那 现在这个角 m o c, 它就变成了这个角 b o m 减去这个六十度了吧,所以它就等于 四分之一,括号五 t 减去六十度。连立这两个等式,我们就能得出要求的。这个角 a o n, 它的表达式 就等于五度,加上四分之五 t b o m 的 表达式有了,角 a o n 的 表达式也有了。所以 四倍的角 a o n 加上角 b o m, 它就等于十 t 加二十度。所以当 t 在 十二到三十六这个时间段内,四倍的角 a o n 加上角 b o m, 它们的和依然不是一个定值半。 那这样我们把第二种情况也就说清楚了。接下来我们再来看第三种情况。第三种情况下,这个旋转角阿尔法,他就在一百八十度到二百四十度之间,也就是说 o m 在 这个角度内旋转。 下面我们来重点解释一下二百四十度这个临界值又是怎么得到的?那其实逻辑跟前面是一模一样的。刚才我们讲过,当射线 o m 转到了这个一百八十度的下面,也就是说它的旋转角度超过了一百八十度,那么角 b o m 就 变成了这个角吧。这个角的表达式呢, 和刚才一百八十度以内的是不一样的了。比如说我们要求的这个角 b o m, 在 这个状态下,它就可以写成 这个周角三百六十度,减去它的旋转角五 t, 而且随着这个 o m 不 停地往后旋转,直到和 o b 重合,这个角度的表达式 都不会发生变化。那么为什么还要分二百四十度这个区间再讨论呢?哎,原因就是角 c o m 的 表达式发生了变化。这个就是这道题最难的一个部分, 我们在考虑分类讨论的时候,是需要同时去思考这两个角度的形式是否都统一。接下来角 b o m 的 表达式虽然统一,但是这个角 c o m 它是会发生变化的呀。同学们看, 当 o m 旋转的位置只要突破了这个二百四十度,比如说 o m 转到这里来了,那么角 c o m, 它就变成了这个角,那显然它的表达是又要发生变化了。 角 c o m 的 表达式发生了变化,那么角 c o n 的 表达式就发生了变化。角 c o n 的 表达式发生了变化,那么角 a o n 的 表达式是不是就发生了变化呀? 所以这就解释了为什么第三种情况下,我们讨论的 om 旋转的范围呢?它是在一百八十度到二百四十度之间,只有在这个区间内同时满足角 b o m 和角 c o m 的 表达式都是统一的。 此时角 b o m, 也就是这个角,它是可以写成这个三百六十度,减去它的旋转角吧?那这个旋转角始终等于五 t 吧,所以角 b o m 就 等于三百六十度减去五 t, 角 a o n, 它就等于角 a o c 加上角 c o n, 对 吧?这个角等于这个角度,加上它,角 a o c 依然是二十度。那角 c o n 呢? 同学们看,它始终等于四分之一倍的角 c o m, 角 c o n, 它是等于四分之一倍的角 c o m, c o m。 这个角度呢,我们可以用这个五 t 减去六十度吧,等于四分之一,括号五 t 减去六十度。 那整理一下这两个等式,就能得到角 a o n, 它是等于五度,加上四分之五 t。 角 b o m 的 表达式有了,角 a o n 的 表达式有了,所以在这个范围内, 四倍的角 a o n 加上角 b o m, 它们就等于四括号五度加上四分之五 t, 再加上三百六十度, 减去五 t, 哎,整理一下,发现刚好等于三百八十度。当阿尔法角的旋转角度在一百八十度到二百四十度之间,此时这个时间 t 就 应该是大于三十六秒,小于等于四十八。 在这个时间段内,我们讲这两个角的和它就是一个定值了,对不对? ok, 再接再厉,我们再来看第四种情况。这个第四种情况呢?这个旋转角阿尔法,它是在二百四十度和三百四十度之间,也就是说射线 o m, 它在这个范围内旋转。 这个三百四十度的临界点又是怎么来的呢?前面我们说,当射线 o m 旋转的位置突破这个二百四十度以后,角 c o m 的 表达式就发生了变化吧,它就会写成角 c o b 加上角 b o m, 再往后,比如说当它转到这个位置, 那么角 c o m 的 表达式还是和刚才是一样的吧。那么为什么还要框定一个三百四十度的临界点呢?这又是一个非常容易出错的点,原因就是当射线 o m 在 这个范围内旋转和在这个范围内旋转, 射线 o n 的 位置会发生变化, o n 的 位置发生变化,角 a o n 的 表达式不就发生变化了吗?比如说,当这个 o m, 它恰好转到了三百四十度这个位置, 这里原来是六十度,那这个角度它是三百四,所以它就是二十度,这个角是八十度。我们又说 o n 始终是角 c o m 的 四等分线,那此时这个 o n 它就会和这个 o a 重合,哎, 对不对?好,这个角等于它的四分之一射箭 o n 和 o a 是 不是重合啊?所以 o m 再往上转的话,那 o n 就 会跑到这个位置。所以这就引出了下面我们需要讨论的第五种情况, 当旋转角 r 大 于三百四十度,小于等于三百六十度。第四和第五种情况主要考虑的就是射线 o n 和 o a 的 位置状态,这里对应的时间 t 的 范围呢, 它就是大于四十八秒,小于等于六十八秒。那这里对应的时间 t 呢,就是大于六十八秒,小于等于 七十二秒。那么接下来同学们需要做的就是分别在这两种情况下,把角 b o m 的 表达式和角 a o n 的 表达式分别给它写出来。比如说在第四种情况下,那角 b o m 的 表达式 和前面是一样的吧,它始终等于三百六十度减五 t, 那 角 a o n 呢?它就可以写成角 c o n 减去角 a o c。 那 再往后整个的处理方法和前面我们讲的三种情况是一模一样的, 所以接下来计算的过程就交给你们了啊,如果同学们听懂了的话,我相信这个第四和第五种情况你们肯定能够搞定啊。那最终计算的结果,第四种情况下呢,这俩角的和不是一个定值,但是在第五种情况下,求出来这两个角的和是一个定值,等于二十度。 那到这里,我们就把这道题的五种情况给同学们全都说清楚。那希望这道题呢,同学们自己一定要花时间好好的去消化一下啊,最好听完以后呢,自己把这道题完整的再做一遍,看看你能不能做到清晰明了的把五种情况都分别写出来。 以上就是本节课的所有内容,复盘一下。在处理动角问题的时候,核心思路就是做好分类讨论,而分类讨论的关键就在于处理好射线旋转是否超过一百八十度这一个分界点。 当然,如果题目中出现了等分线,那等分线的位置也是需要注意的。这节课就讲到这里,咱们下节课再见!拜拜!
3.7万Tom张数学 08:58查看AI文稿AI文稿
08:58查看AI文稿AI文稿十三题大家自己先看看啊,你把它当做个填空题去做吧, 也不要去蒙,也不要去猜了。好,这个题一起来看一下吧,让你们自己做,估计这个很难全部做完,因为难度比较大啊,这个题要真正考就他就得考填空啊,然后就很多人就可以选择放弃了,是吧?就觉得性价比太低了, 也没那个时间搞。来我们看一看啊,他这个至少有一组边互相平行,那是要分类讨论的对不对?每一个边都有可能跟另外一个边平行,但是好处是,比如说你看这个边, 这个边因为和 b、 c 和 ab 都有一个交点,是 b 的, 所以说它是不是跟它们俩不可能平行?所以 b、 d 是 不是只有可能跟 a、 c 平行?好一种一种来啊? b、 d 如果平行于 a、 c, 接下来这个题有一个问题,就是你要画图,知道吗?如果你不画图,你这个光号肉眼看你可能不知道怎么看 b、 d 平行于 a、 c, 我 们想想大概是怎么样 的,是这样子吗? 是不是这样子?好,此时他和他平行吧。好,那平行,那头角相等,这是九十,这个是不是九十? 好,这个是九十,我们要知道这里是四十五度,所以这里是不是就是四十五度?问这个 a、 b、 e 的 角度是不是就是这个?那是不是四十五加三十, 是不是七十五度?第一个答案, 第一个能听懂吗?没问题吧?好 啊,实际上要求 a、 b、 e, 它不是说一定要指出 a、 b、 e, 因为 a、 b、 e 是 个什么,其实就是个旋转角,你以任何一个边为那个基准求旋转角,其实都没有问题,知道吧?第二种情况,那我们就再求一个 b e 为那个基准,求旋转角,其实都没有问题,知道吧?第二种情况,那我们就再求一个边为那个直角,求旋转角,其实都没有问题,知道吧?第二种情况,那我们就再求一个边为那个 c, 因为 b、 e 这条边和 b、 c 和 ab 是 不是都有交点?所以它在旋转的过程中是不是也只能和 a、 c 有 可能平行吧?是不是?那 b、 e 平行于 a、 c 应该是到什么情况?转转转转转转转转,一直转到 这个样子对不对?好, b、 e 转到这个样子,你就把图画出来, 是不是现在这样抓住平行, 那么内错角相等九十度,这里是三十度,所以说此时是不是一百二, 对不对?好,这第二个答案,第三个答案,这个前面我们都 讨论过这个 b、 d 和 b e 了,这两个其实是相对简单的啊,接下来就是最不简单那个了,就是谁,就是这条边, 这一条边,我们看其实跟这三条都有可能会平行,对吧?好,我们一个个来。第一个 d e 如果平行于 a、 b 是 什么时候?是不是当这一条边啊?继续往上转,转到它水平线的时候, 是不是这样子?好,此时多少度? 这个是四十五吧,那这个是内拓展商,等于是四十五吧,所以是不是转了四十五度?你看,第三种情况已经出来了,接下来第四种情况, 大家先听吧,我觉得你可能记的话,你画图画不过来,明白吧,对吧?你这个时候画图画不过来,先听好吧,课后呢,自己再找个空白纸,好好的把几个图画一画,我觉得这样你不要同时做两件事情啊。呃, 再看下一种情况,下一种情况 d e。 就 挨着来呗。比如说 平行于 b c。 那 长什么样? 长这样, 是吧?它们俩平行。好,它们俩平行 同旁,内角互补,这是九十度,这是四十五,这就是四十五,这是三十,所以这个角是多少度?是七十五度, 七十五度重合了,对吧?也,这个答案出现两次了。最后一种情况, d e。 平行于 a c 好, d e 平行于 a c。 我 们来看看啊。 最后一个情况是最难的, d e。 我 们看一下,它现在是这样的, 然后转着转着就变成这样的,然后这样的,然后这样的,这样的,这样的,这样的。是不是当他转到这个方向的时候,是不是可能是跟他平行的?好,我们把这个图画出来啊,就是在这些这个题目中啊,画图其实是一个很重要的一个 事情啊, 他最后是这样的。 好,那这个图是这样平行,怎么求这个角呢?那你要抓住啊,因为两直线平行,所以内错角相等。现在有一个问题啊,我先问大家一个问题,这个角 和这个角,就我图上标示这两个角,你们看我图上这两个角是内错角吗? 大家觉得它俩是不是内错角? 目前来说还不是,因为我们从来没有说过这一条线和这条线是共线的吧, 因为我们只是把这个三角形旋转过来,使得它和它平行。从来没有说过这一条和这一条是连起来的吧?就它有可能是有角度的,对不对?所以这个题很关键啊,虽然最后可以证明它这条直线,但你不能认为它就是, 那怎么证明呢?是这样的,现在因为平行,那么我假设我先不知道它们是不是共线,我延长 c、 b 应该会和这一条线 相交,有一个交点,这个交点这个角才是和它是内错角,是九十度,而因为原来这个角正好就是九十度,所以说明这个点和原来这个点是同一个点,说明三点共线 啊。我说这个细节不知道多少同学能听进去啊,这是你们可能自己想不到的点, 就说这里,我实际上证明了一个 c、 b、 d 三点共线, 知道吧?啊?当然如果说你是就单纯是一个选择题啊,那你就认为它是一条直线,你只要图画得准,那也无所谓。 好,所以这个地方其实是一条直线,那么这里是四十五,这里就是一百三十五,再加上原来的三十,所以这个就是一百六十五。 刚还有个答案或或四十五度的,对不对?所以最后三个四个答案,五种情况啊,其实最后是五种情况,四个答案。想参加我们 teo 训练营的家长可以在评论区留言哦。
 05:28查看AI文稿AI文稿
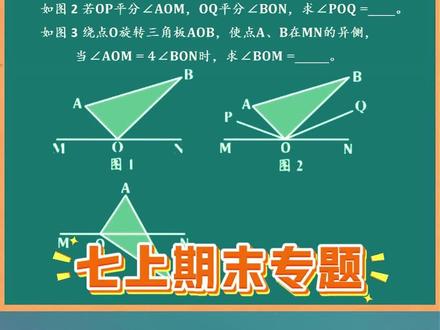
05:28查看AI文稿AI文稿大家好,今天我们一起来看这道去年初一期末考试的压轴题。这是一道和三角板有关的动角问题,综合了多个重要考点。我们先来读题这块三角板 aob 直角顶点 o 在 直线 m n 上, 那角 m o n 就是 一个平角一百八十度。另外,三角板 aob 中角 aob 是 直角九十度。 注意,这是两个隐藏条件,很重要,我们后面会反复用到。先看第一问,图一中三角板是这样放的,点 a 和 b 在 直线 m n 的 同一侧,已知角 a o m 是 四十度, 求角 b o n 是 多少度。你看,整个平角 m o n 被分成了三部分,角 a o m 中间的直角 a o b 和角 b o n, 所以 角 b o n 就等于平角一百八十度。减去角 a o m 四十度,再减去直角九十度,算出来等于五十度。 这一问很简单,对吧?这其实是为后面做了一个铺垫。接下来看第二问,看图二多了两条角,平分角 a o m o q, 平分角 b o n。 问我们角 p o q 的 度数。 这时很多同学会犯难,角 a o m 和角 b o n 没有给具体的度数啊,这怎么求?别急,这恰恰是这道题想考察我们的核心方法,设而不求,以及一个经典的双角平分线模型。 既然不知道,我们就设未知数。设角 a o p 和角 m o p 都是 r, 法那角 a o m 就是 二 r。 法同样的设角 b o q 和角 n o q 都是贝塔,那角 b o n 就是 二贝塔。 还记得第一问的结论,不?角 a o m 加上角 b o n 就 等于平角一百八十度,减去中间的直角九十度,等于九十度 用,而法和贝塔表示就是二,而法加上二,贝塔等于九十度,两边同时除以二,而法加贝塔就等于四十五度。 这个式子先放在这,待会要用。现在看我们要求的角 p o q 观察图形,它是由哪几部分拼起来的呢?角 a o p 也就是而法加上中间的直角 a o b 九十度,再加上角 b o q, 也就是贝塔。 看而法加贝塔这个整体我们刚才已经算出来了,等于四十五度,直接代入四十五度,加上九十度,等于一百三十五度。 这就是设而不求的妙处。不需要算出阿尔法贝塔单独的值,而是用阿尔法加贝塔这个整体。大家看,无论三角板具体转成什么样,只要 a b 在 m n 同侧,这个布局不变,角 p o q 的 度数永远是一个固定值,一百三十五度, 这就是动点问题中寻找定值的典型思路。继续看第三问,图三是旋转后的情况, a 和 b 跑到了直线 m n 的 两边了, a 在 上方, b 在 下方。问,当角 a o m 是 角 b o n 的 四倍时,求角 b o m 是 多少度。 图形变了,但核心条件没变,角 m o n 依然是平角一百八十度,三角板的直角 a o b 也还是九十度。根据角 a o m 等于四倍角 b o n, 我 们设小角 b o n 为 x, 那 么角 a o m 就是 四 x。 因为角 a o b 是 九十度,所以角 a o n 就是 九十度。减 x, 又因为角 m o n 是 平角,所以角 a o m 加上角 a o n 等于一百八十度,代入得到方程四 x 加上九十度,减 x 等于一百八十度。解这个方程 x 等于三十度, 也就是角 b o n 等于三十度。题目让我们求角 b o m, 我 们看图,角 b o m 和角 b o n 刚好凑成一百八十度,互为补角, 所以角 b o m 就 等于一百八十度。减去角 b o n, 三十度等于一百五十度。 那这道题我们就讲完了。最后一起来回顾一下这道题的三个得分密码。一、抓引含条件,这是解析的起点,平角一百八十度和三角板的直角九十度。 二、用模型思维。第二问是典型的双角平分线模型,遇到这类问题,要敢于设未知数。三、掌握设而不求, 这是处理动角问题的利器,我们设出未知数,而法贝塔不是为了单独求出他们,而是为了求出他们的和,而法加贝塔这个整体,从而解决问题。 希望通过这道题的讲解,大家能对动角问题,角平分线模型有更深的理解,我们下期再见。
64张云数学思维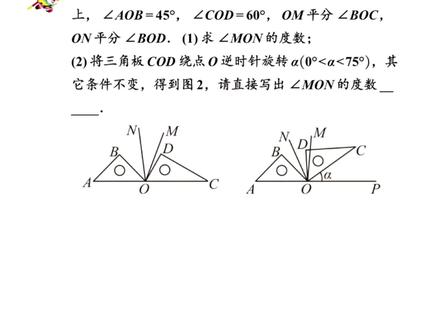 02:43查看AI文稿AI文稿
02:43查看AI文稿AI文稿期末数学想拿高分,压轴题一定要搞定,今天我们就看一道七年级数学的动角问题,听完之后再把这套压轴题练习拿去巩固,选择、填空压轴,还有解答题压轴都包括在内。我们看一下这道题, 把一幅三角板按照图一摆放,使得他们在同一直线上,这里是四十五度,这个角是六十度。 o m。 平分 b o c, 这里是 o m, 那 就说明这两个角相等。 o n 平分。角 b o d, 这里是 o n, 那 b o d 是 这个角,所以这两个角就相等。第一小问,求 m o n。 的 度数。 m o n。 这个角在图里看一下,你可以用这个红色的这个角减去蓝色的这个角,那剩下的就是角 m o n, 所以角 m o, n 是 等于角 b o m。 减去角 b o n, 这里的 b o m。 是 等于二分之一的 b o c, 所以 这里就是二分之一的角 b o c, 这里的角 b o, n, 那 就是二分之一的角 b o d。 最后计算一下,那首先就是这个角 b o c, b o c。 在 图里看,它应该就是这个角,那就是这个平角一百八,去掉这一个四十五度,那就是一百三十五度。 再看这一个角 b o d, 它可以用这一个平角去掉这边的四十五度,再去掉这个三角板的六十度,所以 b o, d。 应该是七十五度,这里计算一下,那就是一百三十五度, 减去七十五度,所以结果就是三十度。第一小问,角 m o n, 它就是三十度。第二小问,它现在把三角板 c o d。 旋转到了这么一个位置,旋转了 alpha, 它告诉你 alpha 是 在零到七十五度之间,其他条件不变, 让你写出角 m、 o, n 的 度数,先把这个其他条件标上去,就是这两个角平分线 o, m 是 平分 b o, c, 这里是 o m, 这是 b o, c, o, n 平分 b o, d, 这里是 o, n 平分这个 b, o, d。 现在想求 m o, n, 同样我们就用红色的这个角减去蓝色的这个角,那剩下的就是 m o, n 的 这个角, 所以角 m o, n 等于角 b o, m。 减去角 b o, n, 下一步还是把它换掉。 b o, m 就是 二分之一倍的 b o, c, b o, n 呢?就是二分之一倍的角 b o, d。 下面把角 b、 o, c 算一下, b、 o, c。 是 这么多, 那就是用平角一百八减去这个四十五度,再减去这一个 alpha。 所以 b、 o, c。 应该是一百三十五度,再减去 alpha。 下面算一下角 b, o, d, b、 o, d。 在 图里看一下,它就是这么一个角, 先用这个一百八先减掉这个四十五度,再减去这个 alpha, 再减去这个三角板的这个六十度的这个角,剩下的那部分,它就是 b o, d, 那 就是这个角。所以这里算一下,一百八去掉四十五,去掉六十,那还有七十五,七十五,再去掉 alpha, 所以 就是二分之一乘以七十五度减去 alpha。 这里计算一下, 二分之一提走之后,那括号里面应该是减去七十五度,再加上 alpha, 所以 最后你这个 alpha 会抵消掉,最终的结果你算出来还是等于三十度,所以这里 m、 o, n 的 度数,其实它是不变的。
22数学老孙 02:31查看AI文稿AI文稿
02:31查看AI文稿AI文稿动角问题中的三角板旋转,在七年级期末考试中一定会出现这类题,通常会和角平分线结合在一起。最后考察的是一个定值问题,就比如这道题, 把一副三角板拼在一起,那这里就是四十五度的,这里就是六十度的那个三角板。现在把这个 c、 o、 d 固定不动,那就是这个六十度的固定不动。将 a、 o b 绕着 o 点,以每秒五度的速度旋转,那就是往这边旋转。在转动的过程中,三角板 a、 o b 一 直在 e、 o d 的 内部, 那 e、 o d 就是 这里,就是它在这个范围内旋转,设时间为七秒,现在告诉你 o m 平分 b o e, 这是 o m 平分了 b o e, 那 说明这两个角相等。 o n 平分 a o d, 这里是 o n, 它平分了 a、 o d, 所以 这两个角相等。题目最后说,在旋转的过程中, m o n 的 度数是否会发生变化,那么 m o n 就是 这个角,这里的这个 m o n 这个角,我们可以怎么求呢?我们可以用这一个大角减去黄色的这个角,再减去这边绿色的这个角, 那么剩下的部分就是这个角 m o n。 这一个角很容易求,因为你这个是六十度,所以这个 e、 o d 呢?那肯定就是一百二十度。所以我们现在需要把这个绿色的和这个黄色的角求出来, 先找到它的旋转角 o a。 一 开始在这里,那现在 o a。 到了这里,它的速度是五度每秒,所以它旋转过的角度,那这个角就是速度乘以时间,那就是五 t。 所以 这个绿色的角,这个 e o m, 它就等于二分之一的 b o e, 这个角 b o e。 在 图里看一下,它可以由这一个四十五度的这个三角板再加上这一个五 t, 所以呢就是四十五度加上五 t, 这个是 e、 o m。 再看一下 d, o, n, 它是等于二分之一的角 a o d, 那 这一个 a、 o d 怎么求呢? 因为我们知道这个 e、 o、 d 这个角肯定是等于一百二十度的,因为你这个三角板,这里是六十度,那它旋转过的角度是五 t, 所以 用一百二十度减去这个五 t, 那 剩下的就是 a o d, 所以 它就相当于一百二十度减去五 t, 那 最后这个角 m、 o n, 它就可以用这个 e、 o d 减去这个绿色的部分,那就是 e o m, 再减去这个 d, o n, 所以 最后剩下的,那就是这个角 m、 o n 的 度数 e, o, d 呢?它就是一百二十度。把 e、 o m 这一部分带进去, d, o, n 这一部分也带进去。最后去括号化减一下,这里就是二十二点五度。减去二分之五 t, 这里是减去六十度, 这里是加上二分之五 t, 所以 最后发现这里的角 m、 o, n, 它的度数是不会发生变化的,它就是三十七点五度。
872老孙数学 02:58查看AI文稿AI文稿
02:58查看AI文稿AI文稿初一上学期你必须学会的两种数学思想,一个是整体思想,一个是分类讨论思想。那咱们再通过这道三角板旋转的问题,练习一下分类讨论的思想。 角 aob 比上角 boc 是 一比二,这是一个平角,一比二立刻算出这个角是六十度。将一个直角三角板顶点放在 o 处, o m 这条边和 o b 重合, o n 放在下方,现在我要把它绕着 o 旋转一周,旋转的速度是十五度每秒。 说当这个直角边 o n 所在的直线恰好平分这个角 a o c 的 时候,让我们直接写出三角板绕 o 旋转时间 t 的 值来。你读完题之后,你觉得哪个字眼最重要?打到评论区, 这个字眼最重要,它说的是直角边 o n 所在直线恰好平分它的时候,你一定要关注题干中的一些限定词,那这就是限定词。你要想这种压轴题拿满分,你必须具备两个满分意识,第一个是便利的思想,第二个就是关注限定词。 便利的思想指的是你必须让 o n 旋转一周,整个这一周的所有的情况你都考虑到了。哎,那满分跑不了了。我们来看,那这道题动的是 o n, 不 动的是什么?我们一定要从不动的啊,简单的情况入手,不动的是什么? 谁平分这个角 a o c 是 不是永远是不变的呀?那老师画出来的这条红色的线,是不是就是平分 a o c 的 所有的直线了?就这么一条,对吧?这里是三十度,三十度。 现在我们要想让 o n 所在的直线恰好平分 a o c 是 不?这个问题就转换成了你 o n 在 转一圈的过程中,只要和这个红线有重合, 那就是我们要的情况。好嘞,我们再看图,是不就非常简单,从这里开始转到这第一次重合,然后继续向后转,再转到这第二次重合, 两种情况,再继续转转转,转到这是不是一周就转完了,我们就变力了。然后在整个一周的过程中有这两种情况,那接下来咱们就算转的角度,再算时间就可以了。第一种情况, 转到这里,那这个角这是三十度,所以这是三十度。对顶角相等九十度减三十度,剩的这是六十度,速度是十五每秒,所以六十除以十五四秒。第二种情况,那从这是不是继续转了个平角,转了个一百八, 等于十六秒,这题满分就是四秒或十六秒,跟着明笛轻松学习。
353初中math铭迪老师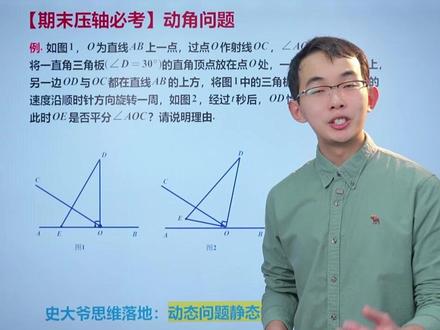 03:31查看AI文稿AI文稿
03:31查看AI文稿AI文稿期末压轴必考的动脚问题啊,难倒了全班百分之九十五的同学,如果你掌握了这个方法啊,其实这类题呢,很容易来处理好,我们一起来看一下这样的一个典型的例题啊,他说有图一啊, o 为直线上 ab 的 一点好,这块有点 o 啊。 然后呢,做一个射线 o c, 好, 首先给你一个角度了啊,说 a o c 的 这个角啊,等于三十,好,所以我们先把这个角画出来,哎,三十度我们是已知的,对吧?接下来啊,有一个直角三角板啊,说上面这个角呢,也是给我们固定了,对不对,有没有用再说啊,反正我们先已知一个条件好, 把顶点顶在这个点 o 的 位置啊。接下来呢,开始进行旋转了,发现,哎,它这个三角板啊,绕着点 o, 以每秒五度的这个速度呢,往右边来掰,对吧?你比如说这个 o d 这条线啊,它要逐步的往右边来旋转,你要转到这转到这,转到这,对吧? 好,随着旋转的时间,它是不一样的啊。好,接下来他问,说经过一定的时间啊,说 o d 啊,恰好平分了 b o c。 然后呢,问你 o e 是 否也平分另外一个角 a o c。 其实这道题虽然是一个动角问题,但是我们发现题目里边其实没有问我们任何关于速度时间转到什么位置的一个情况,对吧?他只是给我们了一个特定的固定条件,问我们是否这个条件能够满足另外一个问题。 好了,那么重点的方法叫动态问题静态化啊,因为它本身这道题问的就是一个静态的问题,来,我们来分析啊,它说首先一个重要的时间节点是 o d 平分了 b、 o c, 那 么往右掰的过程当中, 谁在动,谁不动,这是我们第一步要做的事情。好,只有这个三角板在动,那么你看 o c 这条线动了没?根本就没动,对吧?好,所以这个东西呢,是个定的, o b、 o a 动了没,也没有动,这两个东西也是个定的,所以他说平分了 b、 o c, 那 么这个角是固定的,那它的角平分线也是一个固定的位置。 好,这个角多大呢?人家给你了,说 a、 o c 这边这个角是三十度,对吧?那么 b、 o c 跟 a、 o c 是 互补的, ok, 这个角总的角是一百五十度,那么一百五十度平分一下,除以二等多少? 七十五度,所以,哎,两边都是七十五,好,没有问题,这是我们的得到的一个第一个条件,那么这个条件怎么跟这个 o e 去连接啊?你看 o d 现在是平分线,这边七十五,这边七十五,没有问题。好, 这个 o e 和 o d 呢?我们看它是一个直角三角形的关系,这块肯定是一个垂直的,你这三角板转,你不管怎么转,你这个角是不是永远都是个垂直的呀?对吧?你不可能有其他的变化啊,所以你看有一个直角,其中呢,这边是七十五,那么剩下这边小角落多少? 十五度,对吧?好,所以这个小角就是十五度,那么我们又知道了,整个的大角是不是角平分线, 确实是角平分线啊,所以呢,最后这个答案肯定是确定的。所以这道题,其实你看,它虽然是一个动角问题,但是它其实是一个假的动角问题, 它本质上是一个动态问题,静态化的一个出题方式以及我们的思维过程。所以呢,很多题目啊,大家不要被它的外衣所迷惑啊,一定要学会识别它里面具体的问题和信息。好,这道题你学会了吗?
490清华史大爷数学思维





