上海数学二模24题解题技巧
粉丝2017获赞1984
相关视频
 00:52查看AI文稿AI文稿
00:52查看AI文稿AI文稿矩形二缺二唯一性的问题,如果有两个定点 a、 c 和一根轴,现在需要在这根轴上找一个点鼻,使得仅有一个点鼻能构成矩形 a、 b c d。 这个问题可以转化为直角三角形 a b c 去 a c 的 中点 m, 那 么点鼻就在以 m 为圆心,以二分之一 a、 c 为半径的圆上。那如何保证只存在一个点鼻呢?那就让这个圆和 x 轴相切切点,即点鼻,这时 m 鼻和 x 轴垂直。所以这类问题的解决方法, 先用中点坐标公式求出 a c 的 中点坐标,再用两点间距离公式求出 a c 的 长度,然后令点 m 的 纵坐标的绝对值等于二分之一 a c 的 长度,也就是圆的半径。然后你就能求到你想要的东西,学会了吗?
28小阳哥 08:07查看AI文稿AI文稿
08:07查看AI文稿AI文稿好,同学们,我们一起来看一下,去年这个二模的这个二十四题,是一道新定义的题型,那么这是我们现在考试的一个趋势,也是拉开差距的一个地方。那么有很多同学不适应的就是在于对于新定义是无法理解, 那么这道题的新定义呢?相对还好理解一些,他说横坐标与纵坐标呢互为导数,就称为导数点,那么他说这个直线 l 呢?有且只有一个导数点,即作点 p, 那 么我们要翻译一下什么叫有且只有一个导数点。那么首先这个直线经过导数点呢?我们可以设这个 p 点 x x 分 之一, 那么因为他在这个直线上,所以你大胆往里面带,那么 x 分 之一就应该等于负 x 减 c。 好, 做到这时候大家应该可以去思考,其实就是在解一个什么分式方程,那么你应该要知道, x 肯定是不等于零的,所以两边可以去同时乘以负 x, 那 么得到一等于 x 平方加上 x, c, 整理一下,应该是零等于 x 平方加上 x, c 再加上一。而大家去思考什么叫有且只有一个倒数点,说明只有一个点,屁,所以你也只能得到一个 x, 所以 应该接下来的思考就是,第二,他等于零 啊。这一步可能有些同学是没有想到的,那么得到 c 方减四等于零, c 等于正负二,又因为 c 大 于零,所以 c 等于二。 好,那么第一问,这个 c 把它就求出来了。好,那么 c 如果求出来了,我们把这个带到方程里,是不就是 x 平方加上二, x 加一,所以解得应该 x 等于负一,所以 p 点坐标就出来了,应该是负一,逗号负一。 好,那么第一问也是需要一些思考量的,那么第二题啊,第二题有些同学会卡在这个两个,因为他只知道了一个点, p 是 第一问求出来的嘛, 有些同学会卡在两个这个点坐标,怎么把这个方程的三个系数求出来?那么其实这时候要跟大家说,特别要注意,这个 c 应该是同一个 c, 所以 你的这个解析式其实先可以设成 y 等于 x 平方,加上 b, x 再加二。 好,那么这时候 p 点是负一负一, q 点坐标是一逗号七,所以这时候你就应该往里面带,那么这时候你往里面带的话,就应该得到六等于二, a 加四, 那么 a 应该解得等于一, a 等于一的话,所以 b 等于四,所以最后得到的方程应该是 y 等于 x 平方加上 x 再加上二, 好,那么把它配方就可以知道它的顶点坐标,那么就应该是 x 加二的平方减二,所以顶点 m 的 坐标是负二负二, 那么顶点坐标也是一下就求出来了,也是比较简单。这个啊,那么主要是看第二问,他说如果抛物线上是否存在点 n, 使得 p m, n 是 以 p n 为直角边的一个直角三角形, 好,那么这个题我把这个坐标啊重新再画一下,那么先找到顶点的位置,大概在负二负二的位置,那么顶点坐标 a m 在 这。 好,那么与这个 y 轴的交点应该是二开口向上,那么所以大概率可能是这样的一个图形,那 p 点呢,也是在这二次函数上,所以 p 点差不多在这个位置, 他说 pm 作为直角边的直角三角形,那我们肯定知道你的 n 点,起码从视觉上你就知道肯定不会在右边,对不对?一定是在左侧,那么所以这时候就有了第一种情况,因为他没说哪个角是直角, 那么所以第一种情况可能是不是这样的,也就是说你要清楚的知道是不是当这个 p m n 等于九十度的时候,对不对?角 p 是 不可能再成为九十度的了,因为它不可能在右边啊。当角 p m n 等于九十度的时候,好,这时候我们要求这个呃点 n 的 坐标其实非常好求, 我们有两种方法,第一种方法,设 m 的 坐标,因为在二次函数上,那么就麻烦一点 t t 方吧啦吧啦写下来,然后用勾股定律完成一个计算。那么第二种方法呢?我们就用几何的方法啊,通常用的就是一线三垂直,那么做完这个一线三垂直呢?我比如说这种情况, g 点好,这里是 f 点,那么也就说做 n g 垂直于 m f, 做 p f 垂直于 g m 好, 那么如果说我这样去做完垂线,就把它组成了一个一线三垂直,对不对?那么在这个基本模型里,其实我们可以去再啰嗦一下, 就是得到了相似三角形,对不对?因为是垂直垂直的关系,那么所以叉角和叉角是对应的,圈角和圈角是对应相等的, 那么具体论说,我觉得这个可以不用多说,大家能看到这里应该都明白,那么所以三角形 n 及 n, m 及 n 应该是相似于三角形 p m f 的 好,那么在这个里面我会发现一件事情啊,呃,我可以先不说相似比,但是我会发现 p f 的 长度就是 p 点的纵坐标与 m 点的纵坐标之差,哎,应该是等于一的,对不对?因为 f 点的坐标啊,因为 p 点的坐标是不是负一负一啊, 对不对?大家会一下, p 点坐标是负一负一,然后你的这个 m 点是负二负二,对不对?所以 p f 等于一, 我发现 m f 也等于一,那么说明 p f m 是 个等腰直角三角形,那么对面的 m g n 也一定是个等腰三角形,所以我可以得到的结论是, n g 等于 m g。 好, 那么这时候我其实只要把 n g 的 点坐标表示出来就可以了,那么就是 n 点的纵坐标 减去这个 m 点的总坐标,那么这个时候我就得到了,是不是啊?我先把这个坐标设一下,设 n 点是 t 对 不对?逗号, t 方加四, t 加二,那么所以 n g 就 应该是 t 方加四, t 加四,对不对?好,那么我的这个,嗯, m g 我 们就应该是它的横坐标相减,对不对?那么就是负二减去 t, 因为这时候你特别要注意,一定是在这个第三项线 t 一定是小于零的,对不对?第二,第三项线 t 一定是小于零的,那么把它规定好解这个方程, t 方加五, t 加六等于零,那么得到 t 加二乘以 t 加三等于零,所以 t 一 等于负三。 好,那么这时候发现 t 等于负二,就舍去,因为这是跟原来的点重合了,好,那么把它回代,是不是我们的 n 点就出来了,所以我们的 n 点应该是负三, 然后你把它进行一个计算,应该算出来是正好是负一,好,那么第二种情况我就发现,哎,那么是不是角度有变化了?是不是 当我的这个呃 m p n 等于九十度的时候,哎,当这个角是九十度时候,方法是不是一样的?其实好,那么这时候也是一样做一条垂线下来,是不是一样的方法做 n h 垂直于 p f, p f 是 不是也是垂直于 n h, 那么同理是不是三角形 n h p 是 相似于三角形 p f m 的, 那么一样的点坐标的表示是不是应该得到 n h 等于 hp 啊,对不对?这时候 n h 去表示出来,应该是 t 方加四 t, 这时候应该是减负一,是不是变成加三了, 那么应该等于负一减 t 好 解,这个方程 t 方加五, t 加四等于零,那么得到 t 加一乘以 t 加四等于零,好,所以 t 一 等于负一啊, t 二等于负四,那么负一这个点也是重合的,所以舍去, 那么这时候再回代,所以 n 点的坐标应该就是负四,等号回代进去应该就是二,所以最后两个答案就是负三,负一和负四二。那么这道题整体的难度呢?其实还可以,主要是尝试 对于第一问的这个新定义的理解,大家一定要这个呃,把题目给真的弄懂,那么在第二问中的这个主要第二问相似,其实用到了我们的基本模型,一线三垂直加上我们点坐标的表示,那么其中的关键就是设点坐标的时候一定要注意是 t 小 于零,然后点坐标一定要表示对, 那么对于这道题,如果大家有别的方法,也可以留在评论区或者在后台私信我哦,十天可以改变很多,当然你也可以。
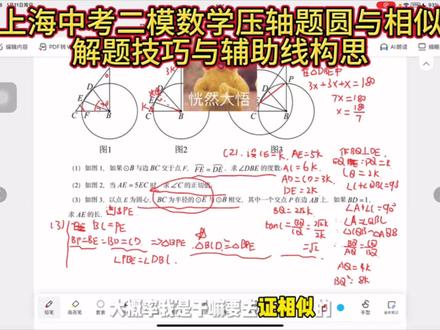 11:19查看AI文稿AI文稿
11:19查看AI文稿AI文稿同学们,我们一起来看一下这个二模啊,关于相似与圆的这样的一道亚洲题,那么这道题我是推荐大家去做,这个亚洲题就是由简单到难嘛,可以从最开始去尝试做这样的一道题,因为我觉得相对来说, 嗯,是稍微好做一些的。那么来看一下弧,第一问,他说角 abc 等于九十度,然后 b 为圆心, b 的是这个 a c 上的一个中线。好,那么第一问,他说 弧 f e 等于弧抵 e, 求角抵 b e 的 一个度数。好,我们来看一下角抵 b e 的 度数,那么首先我去标记一下,那么也就说我在这个呃打问号的这个地方,这个角度是我要求的, 那么他因为说了这个弧 f e 是 等于弧抵 e 的 对不对?那么意味着我的这个问号是不是下面这个也应该是问号对不对?这两个角应该是相等的吗?对不对啊?那么再看,因为很特殊, a b c 是 个直角三角形, b、 d 是 斜边上的中线, 那么我就会发现,哎,角 dcb 如果是个弧角,那么角 dbc 是 不是应该也是一个弧角,对不对?那么这时候我就会发现有很多的什么等量关系, 是不是有很多角的等量关系,当碰到这种角度关系特别多的时候,我往往推荐大家去干嘛呢?射啊,是射角度往往会来的比较快,来的比较清楚,那我们干脆就怎么样呢?射,我的角 dbe 等于 x, 那 么是不是等于我的这个角 ebc 啊? 好,那么所以说角 dcb 是 不是就应该等于两 x, 对 不对?这个没有太大的问题,因为 bd 等于 dc 嘛,对不对?好,那么所以我是不是能够大家去观察一下,你的两倍角和单倍角构成的是不是叫 deb 啊? 角 d e b 是 不是等于角 e b c 加上角 c 啊?那么是不是就是二 x 加上 x 等于三 x 啊?所以你的角 d e b 是 不是三 x 啊?对不对? 好,这个没有什么太大的问题了,对不对?好,那我们再去观察一下。哎,我的这个 d e b 是 不是等于我的 b e 的, 所以这个我的角 d e b 是 不是等于角 e d b 啊? 哎,那么我就是不是发现了,在三角形这个 d b e 内,是不是三 x 加 三 x 再加 x 应该等于一百八,那么所以是不是七 x 等于一百八?那么是不是解的 x 等于七分之一百八?那么第一问就出来了,虽然答案不太合乎常规,对不对?出了一个很奇怪的一个分数,但是我们制作的过程就是这样的, 对不对?好,我们再来看我们的这个第二问啊,他说这个 a e 啊,现在等于五倍的 e c, 那 么求角 c 的 一个正切值。呃,我们首先不管怎么去想,求正切值一定要放在哪里啊?放在直角三角形内,对不对? 所以我们放在这样三角形这里有个现成的,那我们是不是只要求 ab 比上 b, 呃, ab 比上 bc 啊,对不对?好,那么在这个其中里面呢?我们通过第一问去发现,其实它里面有很多的线段倍数关系,对不对?那么我们可以去总结一下,比如说我如果设这个 c e 等于 k 的 话, 那我的 a e 是 不是应该等于五 k, 对 不对? a e 等于五 k? 好, 所以我的总长 a c 是 不是就应该等于六 k, 那 么 a、 c 的 中点,这个 d 是 中点,所以 a、 d 是 不是应该等于我的 cd 等于三 k, 所以 d e 是 不是应该就等于两 k? 好,那么这样我可以去标一下, c 是 k, d 是 两 k, a d 就是 三 k, 好, 那么我先把它标记出来,可是在这个里面我发现如果只有这个边的关系,我而且不知道这个,呃,角 a 和角 c 这个角度的关系下,我 ab 和 bc 是 没有办法去表示的,对不对? 所以这时候大家去想的一个问题就是我能不能把角 c 去进行一个转换?在这个图里,我只知道角 c 是 不是等于角 d b c 的 其他没有任何信息,那么也不在直角三角形里,那么所以我想到的是能不能把角 c 去放在一个直角三角形里去进行一个尝试呢?能不能啊? 哎,这时候大家是不是想办法要把角 c 放在直角三角形内啊?那么大家去想你的第一个方法,大家第一反应肯定想到过点 d 去做辅助线,但是这时候同样有一个问题,其实你没有 改变他的本质,他的本质是不是还是你做这条垂线是不是本质上还是需要靠 a b 和 c b 啊?因为他其实相当于是中位线对不对?所以这时候大家去想啊,我们很喜欢常规的去做的辅助线应该是干嘛呢?哎,想办法去做一个类似于弦心距的东西,对不对? 好,那么我选择过点 b 去做这样的一条垂线,比如说这个垂足点为 q 点啊,那么第二位,我选择做这个 b q 垂直于 d e, 好, 我选择去做这样的一条辅助线,那么这样我的 t n 它 c 是 不是就转换了?是变成了 b q 比上我的这个 c q 啊? 而且做 b q 垂直于 d e 有 个好处对不对?它是不是相当于弦心距啊?所以是不是 d e 是 等于 d q 就是 d q 是 等于 eq 的, 对不对? d q 是 等于 eq 的, 是不是等于 k 啊? 对,这个,呃, q c, 我 们的 c q 是 不是就应该等于两 k 啊?对不对?好,而且更期待的是什么?我的角 c 是 不是加上 角 q b c 等于九十度?我的角 a 加上角 c 也等于九十度,那么所以是不是这是一个像反八字一样的角 c 是 不是等于角? 这个 q 角 a 等于角 q b 哎,那么所以是不是三角形 c q b 相似于三角形 a q b 啊,对不对?那么所以我是不是得到了一个呃,关键的结论? 是不是得到一个关键的结论,也就说 b q 比上我的 a q 是 不是应该等于我的 c q 比上我的 b q 啊?这其中我 b q 不知道,但是 a q 和 c q 我 是不是都能够表示出来,是不是啊?我的 a q 现在是不是就相当于是三 k 加 k 对 不对? a q 是 不是就应该等于四 k? c q 求过了,是不是两 k? 所以 b q 方是不是等于八 k 啊?那么是不是解的 b q 就 应该等于两倍的根号二 k 好, 那么所以 ten it c 就 有了,等于 b q 比上 c q 等于两倍根号二 k 除以两 k。 最后答案是不是出来了,等于根号二啊?这道题大家去分析,包括是去思考的一个过程,可能就这样子 好,那么再看我们的第三位,他说以点 e 为圆心啊,他说 b c 为半径的圆 e, 注意啊,特别注意,他说以 b c 为半径的圆 e, 那 啥意思啊?看一下以 e 为圆心的这个圆,其中有的这个,呃,半径是 b e 对 不对? 那么你会很奇怪的发现一件事情,居然能够找到现成的半径,没有,除了 b e, 他 说是以 b c 为半径的原意,你没有找到任何一条半径,但是呢, 这时候我们要去看啊,这里面其中有很多的线段相等的关系,我们去观察一下, b p 是 半径, b p 是 等于 b e 的, 对不对? 那么又因为是这个直角三角形斜边上的一半有这样的一个关系,所以是不是等于 b d 啊? b d 是 不是又等于这个?呃, c d 啊?好,那么大家你去看,把这种字母你去圈出来 b p, 会发现你会联想到三角形, 三角形 bpe, 三角形 bcd, 哎,三角形 bcd, 我 发现是现成的,而且这个其中好像就啊牵扯到了题目说的以 bc 为半径这个字眼吗? 是不是啊?那我想到 bpe, 我 干嘛就把 pe 连起来,我就发现 pe 刚好又是什么?又是半径,所以我发现 pe 是 不是等于 pe 的, 所以我想到第三问,干嘛连接 pe? 好, 那么这时候我就发现三角形 bcd 应该要干嘛?是不是全等于三角形 bpe 了?如果你能发现这一点,你做出这道题就特别的快,真的特别的快,因为他这道题目关键的字眼是以 bc 为半径,那么你发现圆 e, 你 去取到半径只有 e p, 是 不是? 那么你得到了很关键的信息,三角形 bcd 全等于三角形 bpe, 这时候你就会发现角 p、 e 是 不等于你的角 dbc 啊, 对不对?大家去想思考一个问题啊,我最后如果要求出 a、 e 的 长,其实求线段的长度无非放在直角三角形里,无非相似,三角形无非全等,就是这种常规的操作手段, 对不对?他不在直角三角形里,其实大家要心知肚明,大概率我是干嘛要去正相似的,而如果正知道题相似,长得像的,大家去看一看,是不是大概率是 d b e 和 a b e 啊,对不对?那么我现在正出来角 b p e 等于角,这个, 呃, d, b, c 啊,不是 d b c 应该是角 c d, b 等于角 c d b。 好, 这两个角是相等的。之后呢,我就会发现一件事情,哎,什么事情啊?我的这个角 p b d 是 不是拆成角 p b d e, 我 的这个角 c d、 b 是 不是拆成了角 a 加上角 p b, 哎,那么大家发现,所以是不是角 a 等于角 d b、 e, 对 不对?所以角 a 等于角 d b e, 所以 这是圈角,这也是圈角,那么角 e 又是公共角,对不对? 角 d e, b 等于角 d、 e、 b。 那 么所以推出来一个重要的结论,三角形是不是 d、 e 相似于三角形 a 比 e 好, 那么这两个相似是不是你就可以推得 d e 比上比 e 是 不是等于比比上这个 a、 e 啊? 好,其中大家你去看 a、 d 的 长度你是知道的是一, b、 d 的 长度你也知道是一, b、 e 的 长度你也知道是一。所以你是不是只需要设 d e 等于 x, 就 能表示出来所有的线段了,对不对?那么你设 d e 啊,我用 t 吧,因为 x 前面设过了, 那么 a e 是 不是就等于 e 加上 t, 那 么所以是不是得到 t 比上一等于一,比上一加 t, 所以 是不是 t 方加 t 加一等于零, 所以应该 t 这个解一下应该是等于多少?是不是二分之根号五减一,那么 t 等于二分之根号五减一, a e 是 不是等于加上二分之根号五减一啊? 那么所以最后答案是不是应该是二分之根号五加一?那么这就是最后一个推导过程啊。这道题总体而言,我觉得难度其实不是特别的大啊,真的不是特别的大,那么关键在于一点,能不能想到在第二稳正切值的角 c 去进行一个转换, 这是第一点,第二点是在你第三问的时候能否去啊,很明锐的捕捉到 e 这个圆的半径,还有一条是不是 p e, 而且给你的很凑巧, b e 等于这个 c d p b 又等于 d b, 嗯,最后找到相似去解就可以。 那么对这道题,如果大家有别的这个思考或者说想法,也可以留在评论区或者在后台私信我哦,时间可以改变很多,当然你也可以。
 10:07
10:07 06:21查看AI文稿AI文稿
06:21查看AI文稿AI文稿好朋友们,我们一起来看一下这个去年二模的这个二十四题的这道真题啊,那么这道题的难度呢?其实还可以啊,但是 有的同学呢,容易这个计算发生一些错误,我们来看一下啊。他说第一问球抛物线那个表达式,那么首先我们看题目很简单,他说与 y 轴交于点 a 零五,那么可以找到这个解析式,就是 y 等于 x 平方加上 b, x 再加上五 好。他说抛物线顶点在 p d 一 项线,且在这个 y 等于二分之一 x 上,那么我们可以利用这个顶点坐标的公式,把这个顶点作为表示出来,那么它的顶点就可以表示成负二分之 b 四, a 分 之四 a, c 减去 b 方, 这是他的顶点坐标,那么带入到这条线上,那么就是四分之二十减去 b 方,应该等于负四分之 b 好, 那么解一下这个式子应该是 b 方,然后应该是减 b 减二十等于零 好,那么再去解这个式子,应该是 b 减五乘以 b 加四等于零,那么解得 b 就 应该等于负四好,那么 b 等于负四解出来之后呢?大家要去注意验证一件事情,因为你的顶点是在第一项线对不对?那么你发现,哎,当 b 等于五的时候,是不是顶点位置就不对了,所以要舍去, 那么所以得到我们的解析是 y 等于 x 平方减四, x 加五好,那么它的顶点是?我们也顺大变写一下 x 减二的平方加一好,那么第一问很快就出来了, 那么第二问他说啊,向上平行直线 l 交抛物线的左边呢是 c 点,右边呢是 d 点,他说当 cd 等于 o p 的 时候,求 c 点坐标。其实拿到这个题呢,我觉得大家第一反应应该是挺好的,因为这道题没有出什么幺蛾子, 而且啊,大家看 c d 平行于 o p, 那 么其实在你脑子里有概念一样的,你做 x 轴的一个平行线,比如说这个平行线是 l 二啊, 做 l 二平行于 x 轴,好,那么这个比如说有个这个交点是 m 点,那么你的这个角 c 啊,角 d c m 其实是应该等于你的这个角 p o, 比如说这个点是有一个 q 是 应该等于角 p o q 的, 对不对?好,那么其实这时候你就会发现,哎,如果我往这里做一条垂线下来啊,好,把这个 q 点换到这里,是不是就是说 c m 应该等于 o q, 因为这肯定是全等的嘛。 h l 对 不对? p 等于 d m 好, 那么所以说你是不是就能够得到?如果你设这个 c 点的坐标是 t 啊,你把它带入解析式,那么得到应该是 t 减二的平方加一,那么所以说你的这个 d 点坐标是不是就可以表示成 t 加二都好, t 减二的平方,那么再加多少?再加一啊,再加二对不对?然后你在干嘛?把它回带到你的什么解析式里是不是就可以了? 好,你把它带入到这个解析式里,应该得到。呃,把 t 加一往里面带的话,应该是得到 t 减一的平方加上一,等于再把这个往你的这个 好,应该是 t 减二的平方加上二,应该等于把 t 加二往你的这个函数里带,是不是就 t 方加一, 那么这个发现你的这个 t 方是不能约掉了,所以最终解出来 t 应该就等于四分之五。好, t 等于四分之五的话,这个 c 点坐标就一下就可以写出来了。 c 点坐标应该是四分之五,逗号十六分之二十五。 那么第一问就很快啊,第二问也很快出来,第三问,其实大家也应该感到很开心,因为他也没有出什么特别大的一个变化啊。他说把这个二次函数向右平移 m 个单位,如果顶点为 n, 然后呢?他的这个焦点是 m 啊,他说 m 如果垂直于 l, 求这个 m 的 值,那么如果做到这个地方,大家想要赶时间,而且你对这道题确实没什么思路,我这时候可以给大家提供一个参考性的方法。 因为我之前其实一直讲过,当两条线垂直的时候,垂直于 l 时,那么其实有个结论是 k m n 是 乘以你的这个 k l 应该等于负一,也就是说当两条直线垂直的时候,它们斜率之积应该要等于负一。当然这个是明确,你在这个上海中考的时候,一定是会扣分的,因为这个相当于是没有教过的。 但没关系,如果你去利用这个想去抢一些时间和分数的话,这样写也是可以的啊。那么直线 l 的 这个解析式呢?你也知道是 y 等于二分之一 x, 所以 你知道了这个 km 的 一个斜率,那么应该是负二,对不对?好,接下来一件事情就非常简单了, 因为它是向右平移 m 个单位,对不对?你原来 p 点的坐标啊,你原来 p 点的坐标应该是找一找应该是多少,是不是应该二,逗号一,那么你向右平移 m 个单位之后,你 n 点的坐标就应该是二加 m, 逗号一 好。这时候有同学说我这个 m 点的坐标该怎么表示?其实大家去想, m 点的坐标最好表示了,大家想,你无论向右怎么移,如果你产生了一个焦点,这个焦点的横坐标是不是一定是 p 点和 n 点横坐标和的二分之一啊?也就是说定在 pm 的 中垂线上,这个焦点,这点大家能不能想通? 那么所以很快就想到了这个 m 点的横坐标可以怎么表示啊?可以怎么表示啊?对,是不是表示为二分之四加 m, 也就说横坐标值和的二分之一,那么它的这个呃纵坐标,你把它带到这个函数的解析式里,那么就应该得到 四分之 n 方加一好,这时候你只需要做一件事情,那么就是可以表示 k 值了,对不对?那么 k 值是不是 y 一 减 y 二除以 x 一 减去 x 二好,那么你 y 一 减 y 二,发现等于多少?四分之 m 方好, x 一 减 x 二,得到负二分之 m 要等于负二 好,那么这时候你解一解就会发现,哎,这不是巧了吗? m 方是不是等于四? m 那 么解得,所以 m 等于四 好,那么第二位,呃,第三位也很快就出来了,当然这个方法是最快的,也是最能够直接去写出来的,呃,但如果说你想去拿到满分的话,这道题按照正规的这个做法,你也是可以去设点坐标, 然后用这个呃勾股定律去完成这样的一个解析的。当然,如果你也有自己的方法,或者说不同的思考方式,也可以在后台私信我哦,时间可以改变很多,当然你也可以。
 07:54查看AI文稿AI文稿
07:54查看AI文稿AI文稿好,朋友们,我们一起来看一下这个二模去年的这个第二十四题,那么这道题也是,嗯,相对来说比较繁琐的一道题。那么来看第第一问, 那么他说这个抛物线是 y 等于 a x 平方减二, a x 减四,它会交在 ab 两点,那么与 y 轴交于点 c, 首先可以确保点 c 的 坐标应该是零,逗号四, 那么因为 o b 等于 o c, b 又在第一象限,那么所以我们可以写出 b 点坐标应该是四,逗号零。好,那么我们只需要把 b 点代入点坐标就可以了,那么得到零等于十六, a 减去八, a 减四等于零。 好,那么这时候解得应该 a 等于二分之一,那么把它回代 y 就 等于二分之一, x 的 平方再减去 x, 再减去四,那么第一问就出来了,好,第二问,他说如果将这个抛物线啊沿射线 c b 方向平移,那么首先要确定是 c b 方向, 所以应该是一个往上走的一个这样的趋势,那么按照他走, c 是 不是在你的这个射线上呢?所以你最后这个落点 c 撇点应该也在这个线上,那么所以大致图像你可以画一画,应该差不多是这样的。 好, c 在 c 撇点这里,那么这个 b b 撇点应该落在这里。好,那么,呃,我的这个顶点差不多就在这里, 应该是炸。差不多这样一个图像,那么 a 撇点跟 b 撇点应该是平行的,对不对?平行于 x 轴的,那么你把这两个连起来之后啊,你就会发现, a 撇 b 撇 c, 这个角跟这个角应该是相等的啊,那么他说这个三角形 abb 撇的这个面积要比三角形 abc 的 面积大三 好,那么这个其实可操作空间还比较大,因为 s 三角形 a、 b、 c 一下就能算出来,我们可以看一下 s 三角形 a、 b、 c 的 面积应该等于二分之一乘以以 ab 为底,那么高是 o、 c, 那么这些数据是都有的。二分之一乘以好,那么前面 b 点坐标,有了 a 点坐标,你可以通过对称轴这个对称轴,你通过对称轴公式负二, a 分 之 b 可以 马上算出来,应该 x 等于一,所以你 a 点的坐标应该是负二,逗号零, 那么所以 ab 的 长度就应该是等于六,所以二分之一乘以 ab, 再乘以 o, c 等于四,那么算出来面积是十二, 所以你可以得到 a 三角形 a 撇 b b 撇的面积应该是十二加三应该等于十五,好,那么在 a 三角形 a 撇 b 撇算的时候,是不是等于二分之一以 a 撇 b 撇为底,然后乘以 啊?是不是你的这个 y a 撇减去 y c 撇,也就说它们纵坐标之差好,那么这时候 a 撇 b 撇的长度是不是还是不变的?是不是二分之一乘以六,乘以二,这个是应该是乘以这个 呃, a 撇的纵坐标好,那么这时候就是得到乘 y a 撇的一个纵坐标,那么所以 y a 撇的纵坐标应该等于五好,那么你把它这个等于五算出来了之后呢,你就可以去思考一下它的这个横坐标应该是多少啊?你可以思考一下它的横坐标是多少, 其实你只要知道它的这个运行运行的这个规律就可以了,因为它的纵坐标现在是五,对不对?那么你需要带入它的这个什么,你需要把它带入你的这个解析式,但是在带入的时候你需要思考一个问题啊,它的这个问题就是它是怎么样移的, 对不对?你要知道它是怎么样去进行一个平移的?哎,对,这里的关键就是你的直线 b c, 你 的这个直线 b 撇 c 撇,或者说在你的这个直线 b c 上,在你的这个直线 b c 上,它有一个规律,也就说这条线你看这个角是不是四十五度啊?是不是四十五度啊? 也就是说,所以说其实你运动的这个轨迹,你可以想想这条线应该是不是 y 等于 x 减 b, 对 不对?好,那么你也可以选择这样去思考。过点 b 撇做一个垂线,随便做一个是 m 点,那么其实也就说你现在是不是往右平移了 t 个单位的话, 比如说你现在是向右,那么同样的你是不是对应着也向上提个单位?好,那么所以说你的这个 c 到 c 撇点是不是向上五个单位,那么也意味着是不是要向右五个单位? 好,那么所以可以得到你 a 撇点的这个横坐标,是不是从 a 的 原来的横坐标向右平移了五个单位,那么是不是得到应该是三逗号五,那么一样的道理, b 撇点应该是九逗号五, 那么所以他的对称轴就是直线 x 等于六,那么第二问就出来了,当然我觉得你在这一问也可以啊,为了第三问也可以先提前写出来他的这个错,呃,就是他的这个解析式,那么他的这个解析式你知道他是怎么样平移了之后,你可以直接先写成顶点式, 应该是 y 等于二分之一的,这个 x 减六的平方,再加上二分之一,这应该是新抛物线,对不对? 它的一个解析式?好,那么现在他说如果 p 是 新抛物线上一点,这个角 a c b 等于角 p b 撇 b, 那 么看一下,首先你要在抛物线上,你可以清楚的知道它不可能在下方吧,这下方这个角你看明显是要小于 就是小于这个角 abc 了,都,对不对?它的角度不可能要比四十五度要大,所以这个 p 点一定是在哪个位置,一定是不是在这边, 对不对?且要是一个锐角,那么是不就这边是合适的,对不对?好,那么这两个角度相等的话,该怎么求呢?所以说通过在第二个我们做的时候,会细心的发现一个很关键的点,也就说我们这个弧角,那么把这个弧角改成叉角,在叉角这个地方,你会发现他是不是都是四十五度啊? 哎,很巧的是,角 a c b 是 不是也是四十五度啊?也就说在这里面你会发现这个角 a c b 是 不是等于角 o c b, 也就是四十五度加上角 a c o, 你 的这个角 p b 撇 b 是 不是也等于四十五度?你的角 a 撇 b 撇 b 是 不等于四十五度,加上角 p b 撇 a 撇。 所以这道题很关键的问题时,就转换成了角 p b 撇 a 撇等于角 a c o 好, 这是一件非常重要的事情,那么这非常重要是因为 teninet 角 a c o 是 不是好算的,是不是等于二比上四等于二分之一啊? 好,那么所以说你也知道了 teninet 角 b p b 撇 a 撇,对不对?好,那么这时候你就是不是可以设 p 点好,我们把它去 这个做个垂线下来,比如说这点是个 g 点,好,那么这时候 p 点,因为在这个新抛物线上,我可以设成 t 逗号,二分之一, t 减六的平方, 再加上二分之一,好,这时候我们是不是只要拿这个 p g 啊?我写到这 p g 比上你的这个 g 撇 b 应该等于二分之一 好,在这个其中 p p g 是 不是就是 p 点的纵坐标减去 b 撇的纵坐标,对不对?那么我们可以书写一下,应该是二分之一乘以 t 减六的平方,再加上二分之一,再减去五除以 g 撇 b, 是 不是他们横坐标之差, 那么 b 撇的横坐标是九,所以应该是九,减 t 等于二,好,那么这时候你经过一个计算, t 应该解出来等于二 好, t 等于二,你把它这个带入你的这个设的点坐标,所以 p 点坐标应该是二,得二分之十七, 那么就出来了。那么这道题的关键就是在于,你要知,通过这个对图像的观察,四十五度的观察,你要找到角 p b 撇 a 撇等于角 a c o, 然后再通过这个,呃,我们设点坐标,通过三角笔进行一个转换,最后进行一个略式计算,就算出来 p 点的坐标是二都好,二分之十七,如果大家有别的方法或者说其他的几何方法,也可以留在评论区或者在后台私信我哦,十天可以改变很多,当然你也可以。
 04:56查看AI文稿AI文稿
04:56查看AI文稿AI文稿朋友们,我们一起来看这个二模的十八题,那么十八题又是一道啊,很经典翻折的题型,那么我们再讲一下这个翻折他到底该如何去翻呢?那么首先他说 e 点在 b c 上,好,我随便找个 e 点,他说啊,沿着 a e 去进行翻折,那我肯定要把 a e 连起来, 那么大家清楚的知道,翻折是不是一定是成一个类似于轴对称的图形啊?那么也就是你的 b 点是关于你的对称,轴对称且干嘛,是不是且垂直的,那么所以 b 点翻过去,是不是我找到了 f 点?好,那么在这时候 b 点翻过去是 f 点,那么这里有一个垂直, 那么我如果把 a f e 连接起来啊,把 a f e 连接起来,那么各位请看啊,照道理来说,这个角是不是应该是个九十度啊?那么我把它放的缩小一点,大家请看角 d, f e 是 不是要等于九十度啊? 好,那么可是在这个时候呢,大家去看啊,这时候要去看题目说的是不是 e f 垂直于 c d 啊?哎,那么这时候比如说有个焦点是 g 点,大家发现问题了没有?这时候你的角 d 及 f 也等于九十度哦,也就是说你在一个三角形里怎么可能会有两个九十度呢? 对不对?所以因此我就知道我的 f 点一定不可能在 c d 的 右边,我的这个 f 点应该是在 c d 左侧,对不对? 因为但凡在右侧的话,是不是两个九十度啊?是不是不可能在一个三角形 d g f 里的,对不对?好,那么所以这个图我就知道了,画错了,不应该在这里。好,那么我经过我自己的推理,我知道了这个 f 点应该是不是差不多在这个位置,好,把它进行一个标注,我把它连起来。 好,那么差不多是在这个位置,然后呢把这个 b f 要延长一下到这里。好,然后呢他说最后要求这个 e c 的 一个长度。好,朋友们,我们看一下,求这个 e c 的 长度呢?我首先看一下,他说要 e f 垂直于 c d 啊,这时候感觉是不是也 不太像了,所以我们把图再调整一下,好,我把 f 点的位置调的像一点,那么差不多应该可能在这里啊,这样的话是不是满足 e f 垂直于 c d 啊?好,这时候我再把这个 a f 连过来啊,那么这个可能是这样的啊, 那么这个垂直在这啊,这边可能有些草率,但是我为了要符合 e f 垂直于 c d 这个图,好,那么做到这个图之后呢,大家请看啊, 这里是一个九十度角,对不对?好,那么我的这个角 a f e 也是一个九十度角,哎,那么同学们有没有想到我这个九十度角,九十度角,哎,我把 af 延长啊,我如果延长 af 这点 g 其实就是交于比 c, 这里我就省略不写了,那么这时候是不是角 e f g 也等于九十度等于角等于好,这边比如说有个焦点是 m 点等于角 emc, 那 么所以是不是 a g 平行于 cd, a d 平行于 c e, 哎,那么这时候我就发现是不是 a 到几 c 是 平行四边形啊,哎,这是个很重要的结论,那么这样的话是不是就得到了 c g 等于 a d 等于三。好,那么在这个里面其实我都是能去解的,对不对?因为为什么?因为我这个 c d 的 长度,其实我也知道,大家想想是不是这个道理, 你看 a g 是 不是等于 c d 啊?那么 c d 很好求你把它这个图形单独剖出来,其实就是过点 d 做一条垂线,这个我觉得我不用多说,那么你过点 d 做一条垂线,应该是能够把这个 c d 通过勾股定律算出来, 对不对? c d 应该是等于五的啊,这个我觉得大家有问题,你可以在这个后台自己找我。那么这个 c d 等于五算出来了之后呢?是不是就 a g 就 出来了? a 级也等于五,那么 a b 是 不是等于你的 af 等于四啊?所以你的这个 f g 是 不是等于二?好家伙哎, f g 也有了, b e 是 等于 e f 的, 那大家这不就想到了吗?是不是很熟悉的解三角形的题目, 是不是?所以说你想到了设 b e 等于 e, f 等于 x, 好, 那么这样的话,是不是 e 级就应该等于三减 x? 好,勾股定律 x 平方等于括号,三减 x 的 平方再加上四。好,这时候你去解一下,你的这个比 e 算出来应该是多少啊?所以 x 应该等于三分之四, 这个很好算, x 方因为都是消掉了吗?好, x 等于三分之四的话,所以 c e 的 长度是不就有了?又减去三分之四,那么最后答案就是三分之十四。 那么对于这道题,我觉得从这个翻折他翻在哪个位置,我也给大家去分析了一下,那么包括后续我们想到去延长构造平行四边形来解这道题。 如果大家对于这个 c d 等于五还有疑问的话,我觉得是要加快对于这个四边形的一个学习了,那么大家如果对于这道题还有别的解法,也可以留在后台或者评论区私信我哦,时间可以改变很多,当然你也可以。
 03:50查看AI文稿AI文稿
03:50查看AI文稿AI文稿好朋友们,我们一起来看一下去年这个二模的十七题啊,这道题呢,其实得分率也不是特别高啊,而且很多同学都没想到啊,这道题到底怎么做?我们来一起看一下,他说啊, af 等于 b e 等于这个四分之一的 b c a d 平行于 b c, 那 我就意识到 af b e 是 不是一个平行四边形, 那么所以我得到的第一个结论应该是 ab 等于 e f 好, 那么他说 f g 呢?又平行于 a c 好, 那么 af g c 是 不是是个平行四边形啊? 那么是不是得到了 a c 等于 f g? 他 说啊,如果 a c 减去 ab 等于 a, 然后他要比较四边形 c g f h 和 a b e h 周长的差。 好,那我们首先去看一下我们的 c g f h 它的四条边的构成。那我们首先大家明确一件事情,我的 c g 和 b e 是 不是一样的?这个没有任何问题对不对?因为 b e 是 不是等于 af, af 是 不是又等于我们的 c g, 所以 说 a b e 等于 c g, 那么我们在明确这个的前提下,我的 c g f h, 我 就把它只写成 c a 加这个 h f, 再加 f g 再加 c g 啊,我还是把它表示出来,我以防大家到时候这个忘记。 好,我们再看这个 a b e h a b e h 的 周长,那么呃,我们的 ab 加上我们的 a h, 加上我们的 h e, 再加上我们的这个 b e 好, 那么其中 c 级跟 b e 是 相等的,我把它划掉,我们现在要比较 c h 还有 ab, 然后还有我们的 h f a h g f 和 h e, 那 么首先去观察一下啊,我们去观察一下他跟我们这个一比四有什么用呢?我们去标注一下, b e 等于 t, c g 等于 t, 所以 这个 c e 是 不等于三 t 对 不对?哎,那我这时候就发现, 呃,前面我写的这个 ab 等于 e f ab 等于 e f, 我 把它找到,好,那我发现 我的其中这个 a c 和 f g 是 不是也相等的?哎,巧了吗?这上面不就有我的 f g 吗? 好,那我把 f g 是 不是换成 a c 啊?那么是不是说明 f g 减去 ab 等于 a 啊?好,那么我首先发现了一组啊, f g 减去 ab 等于 a, 那 么第二点我又发现,哎,因为平行,所以这个 c h 是 不是应该等于四分之三的这个? 呃, f g, 而我的这个 h e 是 不是又等于四分之三的 ab 啊?好,那么所以我又发现,哎, 所以 c h 减去 h e 是 不是正好等于四分之三的括号 f g 减去 ab 啊? f g 减去 ab 是 不等于 a 啊?所以等于四分之三 a, 那么大家现在看,我又找到一组,那么现在是不是发现就差一组 h f 和这个 a h 的 关系了?好, h f 其实跟我们里面的线段又有关系,我发现是不是 f h 应该等于什么?是不是一比三的这个关系啊?所以是不是等于这个三分之一的 h e 啊?好,那我的这个 c h, 我 的这个 h f a h a h 是 不是等于三分之一的 c h, 那 么我就发现这两个一座叉,这不又巧了吗? 是不是等于三分之一的 h a h e 减去 c h 啊?好,那么这是不是就等于负四分之三 a 啊?好,那么所以综合一下,是不是负四分之一 a 啊?那么现在把剩下的长度加起来负四分之一 a, 四分之三 a, 还有一个 a, 那 么加起来是不是正好等于二分之三 a? 那 么这道题考的也是非常巧妙,运用了我们这个平行线段,包括我们这个四边形 的一些性质啊,完成这道题的一个计算。那么大家对这道题还有别的疑问也可以在评论区或者在后台私信我哦,十天可以改变很多,当然你也可以。
 22:26
22:26 04:10查看AI文稿AI文稿
04:10查看AI文稿AI文稿好,朋友们,我们一起来看一下去年这个二模的选择题第六天,那么这道题当时也是难倒了很多的学生,那么大家可以看一下,这道题是原以原为基础模型的,那么他说这个三 b 等于三分之一, b, c 等于十二,那我们做的第一件事情就是可以把这个三条边算出来。 好,那我们可以说 a c 等于 k, ab 等于三 k, 那 么根据勾股定律, k 方加上一百四十四应该等于九 k 方,那么一百四十四,这样应该等于八 k 方,那么 k 方应该等于十八,所以 k 应该解得等于三倍根号二。 好, a c 等于三倍根号二,那么所以我们的这个 ab 啊,算出来就应该等于多少九倍根号二, 这时候他说这个,呃,以 m n 为直径的圆,那我们找到 m n 为直径的圆,那么也就是要找到 m n 的 中点,那么其中他还说 c m 等于 b n, 这时候大家就发现,比如说我这个中点是 n c m 加上 m o 是 不应该等于 o n 加上 b n, 而且这个结论是永远成立的,所以我们得到是不是 c o 等于 b o 好, 那么关键的一点就发现了, o 是 应该是中点 好,那么以 a c 为直径的圆,我们发现好这个简单,它是固定的,那么我们现在固定了点 o 之后,我就发现,呃,他说 m 为直径的圆与 a c 的 圆要相离,对不对? 好,那么还要与 ab 有 公共的交点,那么我先大概划一下这个圆,可能这样啊,满足相交,那么我们要知道满足相交他要有个极限对不对?那么他如果不相交的临界值是不是相当于相切的那个位置啊?对不对?那么可能在这个位置好,那么相切的话,是不是我们是做垂线, 也就是说当这个垂线等于它的半径的时候,是不是就是它的这个刚好有交点的时候,那么我们比如说做的这个就是 o g 垂直于 ab, 那 么这个 ab 是 不是就是应该是它半径的最小值啊?那么这个也很好算,是不是在 r t 三角形 o g b 中, 现在 o b 是 不是等于二分之一的 b c 啊?是不是就应该等于六?那么根据我们的三角比三, b 是 不等于 o g 比上 o b 等于一比三,所以我们 o g 的 长度是不是就是二?好,那么既然 o g 等于二,所以大家想 o m 是 不是这时候就等于二? 好,所以这时候我们的这个 c m 是 不是就等于四啊?好,那么大家要去想一个道理,是不是随着我这个呃 o g 的 增大, c m 会减小,所以我们得出来第一件事情,是不是 c m 应该要小于等于四? 那么这时候排除了哪个选项,三倍根号二就遗憾的被淘汰了,那么这时候我们想还有什么条件会框数它呢? 哎,那么就是满足我们相邻是不是要去比较我们的圆心距,那么连接, ok, 那 么 ok, 是 不是中位线, ok, 是 不是等于二分之一的 ab? 哎,二分之一的 ab 等于二分之九倍根号二? 好,那么这时候我们不妨就设我们这个 c m 啊,设 c m 等于 x, cm 等于 x, 那 这样我们算下我们的半径 o m 是 不是应该等于?呃, 十二减二 x 再除以二是不等于六减 x? 好, 那么一样去,呃,让我们的这个半径之和是不是要小于圆心距啊?那么是不是说明六减 x 再加上 a, c 的 一半,是不是应该是二分之三倍根号二小于我们的圆心距二分之九倍根号二, 那么这样的话,我们去算一下,是不是应该是六减去三倍根号二要小于 x 啊?也就是说 x 是 不是要大于六减去三倍根号二,那么大概应该是个一点几几一点八左右可能 好,那么一是不是排除掉 b 不 再返回,那么综上是不是只有一个复合条件,只有我们 c 选项, 那么这道题也是比较有这个难度的一道题,那么希望大家对于这道题也能有自己完整的一个思考,而不说一定要去排除蒙 啊,一定要去把这个范围去算出来,那么大家还有别的问题也可以留在后台一直在评论区私信我哦,十天可以改变很多,当然你也可以。
 03:44查看AI文稿AI文稿
03:44查看AI文稿AI文稿好朋友们,我们一起来看一下这个二模的这个填空的压轴题是八题啊,那么这道题呢,当时也是得分率不是特别高,因为很多同学没有做到过这样的题目,但题目表述特别的简单,他说在这个三角形 a、 b, c 中角 c 呢等于九十度,好,我大概去进行一个绘画 啊, d 呢是 ab 的 一个中点,那么这个是非常喜欢看到的,那么他说过点 d 的 直线交 a, c 于点 e, 如果 d 以平分三角形 a、 b, c 的 周长好,特别要注意同学们 d 以平分三角形 a、 b、 c 的 周长,那比如说我这么画,那么也就说现在 s 三角形 a、 b、 c 的 周长分成了,是不是应该是两部分啊, 对不对?也就说我的是不是 a、 d 加上 a、 e 啊,是不是应该要等于我的这个 b, d 加上 b, c 再加上 c e 啊? 啊,是不是应该得到这样的一个过程?好,那么有些同学犯的第一个错误啊,他会把 d、 e 也加进去,那么问大家,分割你的这个周长,你的 d、 e 不是 你原来周长的一部分对不对?所以你不能把 d、 e 加上去,这是特别重要的一点,所以你会得到这个式子,那么你又会发现 a、 d 跟 b d 是 不是相等呢?那么约掉, 所以自然而然你就得到一个式子, a, e 应该等于什么? b, c 加上你的这个 c, e。 好, 那么同学们去思考一下,我最后要去求的是什么? d, e 比上我的这个 b、 c 对 不对?哦,那我们知道求线段的比值,我要么把两个线段去算出来对不对?要么可能说放在 a 字形,或者说放在 相似量型里,那么在这道题里什么都没有,对不对?所以我们想办法用 d e 和 b c 用什么同一个字母去表示出来? 好,因为我看到第一点是个中点,所以我自然而然想到,哎,我先去做一条什么中位线啊,比如说我做 d h 垂直于 ac。 好, 同学们,这时候你就会发现一个现象啊, d h 就 等于什么两分之一的 b c。 哎,这时候你发现了,你的这个 d h 和 b c 产生了关联, d h 和 d e 是 不是也在一个三角形里啊? 好,那么这时候我们可以大胆去尝试做一些这个代数上的一个变化。设, b c 等于 x, 那么 c e 等于 y, 哦,那么,所以得到你的 d h 是 不是应该等于二分之一 x, 对 不对?那么也说明了啊,说明了,是不是你的 a e 等于 x 加 y? 好, 大家特别注意 a e 这一段,我把它标出来, 是不是等于 x 加 y, 哦,那么,所以你就发现 a c 是 不是等于二 x 加二 y? 好,你又发现了。哎,因为什么 h 点是不是中点,所以你会发现你的这个 a h 是 不是应该等于什么? 二分之一 x 加上 y? 哎,你又发现你的 e h 是 不是等于 a e 减 a h? 嗯,发生了一件很神奇的事情, a e 减 a h 是 不是正好等于二分之一 x, 所以 你发现 e h 等于二分之一 x, 你 的这个 h d 是 不是也是二分之一 x, 所以你发现三角形 d h e 是 一个什么?等腰直角三角形?好,那么当你发现这个结论,这道题就一下就做出来了,是不是这个道理?好,那么因为你的这个 d h 等于二分之一 x, 所以 你的这个 d y 是 不是就等于啊 d d e, 啊 d e 等于两分之根号二 x, 那 么所以你比一比出来,结果是不就是二分之根号二?好,那么这道题实际上我们用到了一个概念,是中位线构造出来一个直角三角形,那么又用到了我们代数上的一个方法 啊,你只要想办法用这个字母不断的去表示,那么最后一定是能够绕出来的。那么大家如果这道题还有别的方法,你也可以留在评论区或者在后台私信我哦,十天可以改变很多,当然你也可以。
猜你喜欢
- 1628sinα=1
最新视频
- 350信承








