泰安一模立体几何
同学们好,我是小彤彤家大白这个视频我们说一下这份呃贪一膜的物理试卷。 那先点评下这张这份试卷啊。呃,难度是有,但是并不能说得上是很难啊,就是算是有点难度吧,中等偏上的一个难度啊。然后呢,但是它确实不是很好做,延续了贪一贯的模考题的出题风格。就是 啊,单选多多数都是计算啊,咱七个题计算就是啊,七个计算相当于是啊,我记得去年好像有一份卷子 二模还是三模来着,就是八个单选全是计算啊,还是前年来忘了,就很难做,就这样。所以说各位同学可能觉得做的不是很习惯,但其实难度并不高哈,并不是非常高 啊。来说一下啊。首先第一题,这就是送分题了吧,对吧?首先 a, 这个他说的是这是一个什么?这是布朗运动,布朗运动是描述的这个小颗粒的一个无规则运动,而并不是分子本身的小颗粒。呃,分子本身的无规则运动 就这样,哎。布朗运动可以反映分子的分子的无规则运动,对吧?哎,因因为由于分子无规则运动,随之导致这个颗粒做布朗运动,对吧?但是它 并不是这个小碳小碳粒分子在做无规则运动,而应该什么应该是水分子,说明了水分子在做无规则运动,因为是水分子撞击这个 哎,小弹力,所以他才做无不老运动的,就这么东西啊。然后二 b, 这是什么?哎,非晶体,这个没什么好说的,对吧?然后 c c 明显是对的,对吧?哎,他的结构上看在微弯结构上显空间就有周期性,对吧?四 d 呢?就是这个也不对啊,原因是因为有表面的张力, 但是给他的这个力就是把他托住,这个力并不是水面的张力啊。张力是水分子之间的一个引力,相当于是,对吧?就相当于是把这个水面给拉紧,就像那个蹦床一样, 对吧?拉紧的这个力就是张力,但是你站在蹦床的时候先托起你来了,并不是这个收紧的这个力,对吧?所以他是不对的。哎,这是这个第一题哈。
粉丝985获赞6482
相关视频
 05:00查看AI文稿AI文稿
05:00查看AI文稿AI文稿刚做完高三一模的数学卷子,这套题到底算难还是简单呢?我自己啊,是掐时间做的,还专门统计了基础题、中档题、难题的占分。我认为咱们要多去看试卷的优点哈,你偷懒全卷,我必须说,这是一份质量很高,区分度很清晰的模拟题, 它完全符合高考基础题送分到位,中档题区分人才难题选拔尖子的命题、命题逻辑。今天呢,我就带你深度拆解这一套泰安一模式卷,看完你就知道接下来该猛攻哪里了。我们呢,来,按照顺序 看一下这套题。我这里呢,一个三角代表的是基础题,然后像两个三角的就是中档题,三个三角就代表难题了啊。 来,我们先从单选开始看,选择题的一到五题都是基础题,总分题,然后六七题我把它归到了中档里边。因为这个第六题,我看同学对这个条件概率 学的不太透啊,好多出错的。第七题呢,是因为有一点点的计算量,六七都属于中档题。然后最后一个题第八题,实际上哈,他的思路没有很难,因为他数列和函数结合在一起的,好多同学他无从下手。也就是说,单选里边 五个题是基础题,一共占二十五分。最后一个第八题,单选压轴题是难题,占五分。 然后我们再来看一下多选,这三个多选都不是很难哈,第一个多选算到基础题里边,然后二三个多选难度都不是很大,计算量适中, 尤其是最后一个,很容易锁定正确答案,不要把它想太难了。所以,多选里边,第一个多选算是一个基础题六分,然后二三多选,算是中档题,占十二分,多选里边没有难题。好,我们再看填空,填空题里边 基础中档难题各一个,第一个填空送分的第二个填空题,同学们只要细心一些,这五分是可以拿到手的,关键是要细心。最后一个题 计算量就比较大了,计算量大你知道怎么做,但怕你算不出来呀。好,填空题的 基础,中档难题的笔试五分,五分,五分。接下来我们进入到简答题第十五题,第一个简答题完全送分,咱例题几何真的是没有多难过,算到基础题里面,一共占十三分。 第十六题考察统计与概率分布列,简单绝对的基础题十五分。 然后看第十七题一二问,真是没,真是没有一点难度,绝对的送分题。那有的同学他第二问可能,可能三角复习过去的时间有点长哈,不知道怎么处理了。基础问题, 然后第十八题的第一问是非常简单的,很基础的一个题目。然后第二问里边的第一小问求最值,你只需要把这个用未知量把这个三角形的面积表示出来,求最值去就行了。思路不难,但有一定的计算量, 所以我把它归到中档题里边。然后最后一问,好的同学他没思路的,所以他在难题里边,然后看到最后一个题,第十九题的第一问完全是可以做一下的, 第一小问读懂题去算就可以了。然后第二问里边的第一小问求取值范围的也是一个常规题目,虽然常规,但我把它放到中档题里边,是因为他有一定的计算量,你知道怎么做,但不一定算对, 最后一个题一定是放到难题里边了。好了,我们我们总起来看一下,实际上整套试卷基础题占分是最多的,然后我把刚才的那些分值都加起来,最终基础题 占八十二分,中档四十六,难题是二十二分,那基础题占分是相当多的。我所说的基础题呢? 有的同学可能会把它归到中档里边,可能会认为中档题占的比较多,但好多我都归到基础里边了。因为只要是思路不太难,计算量没有太大的,都应当算到基础题里边。怎么算到中档题里边?思路比较简单,但是计算量很大的, 计算量大的放到中档题里边。所以说,如果孩子的成绩不足八十二分,那基础问题一定是很大的。如果能考到一百二十八分,说明真的是没有多丢分,做的是相当严谨的了,一百二十八分以上的就是非常棒的孩子了。
161泰安数学趣谈 02:02查看AI文稿AI文稿
02:02查看AI文稿AI文稿好,第三题,光的双缝干实验,是吧?这个镜子咱们已经遇到很多次了,我就不再解释了哈。在这里我们要用到公式,哎,我们笔记三十三页上得 x 等于 l 比 d 成 lamb 了,是吧?就是,哎,这个 l 是 这一段 是双缝到光屏的间距,对吧?然后 d 是 双缝间距, dx 是 相邻条纹间距,对吧? lamborgha 就是 光的波长,然后这个提示在这中间填了一个戒指,对吧?那么这个 lamborgha 就 成了在戒指当中的这个光的波长,所以说我们就可以把这个公式写成这样,好,我们写一下啊, 那么这个公式显然可以写成得 x 等于,哎。首先是 l, l 是 什么? b 加 c, 对 吧?是双缝到光平的间距, d 是 什么?二 a 乘上 lamb 了,我写个 lamb 的 撇,哎,也表示是介值中的波长,对吧?那显然由此我们可以知道, lamb 的 撇 现在就有了,对吧?现在就是二 a 得上 x 比上 b 加 c, 对 吧?那有了介值波长,我们怎么算这个?这个折率啊,很简单,给了我们真空波长了,对吧?真空波长是 lamb 了,所以说在这里我们的公式啊,三十二页上折率也可以等于真空波长比介值波长, 哎,怎么来的?很简单,其实就可以利用这个公式推出来,对吧? nc 比 v 大家都知道,对吧?那么 c 的 话显然等于什么?是等于 lamb 乘 f, 对吧?哎,真真空中的波长成频率, v 介中波长成频率,而光在穿过不同戒指前后,他的这个频率是不会变的,对吧?所以说,你的这个光速之比,传播速之比就成了什么,就成了这个 波长之笔了,对吧?所以说也可以用这个来算折率,但这个体系就这么个意思,对吧?用它来算折率,所以说显然,哎,这个 n 就 可以等于那么了, b 那 么了撇,对吧?所以我把它代入,然后我们显显然就是什么这个二 b 是 对的,就完事了啊,这是第三题。
153小彤彤家的大白 00:20查看AI文稿AI文稿
00:20查看AI文稿AI文稿高三一模考试前一百名各高中分布情况,泰安一中四十六人,新泰一中十四人泰安二中五人肥城一中十一人东平高级中学十一人东平明湖中学四人宁阳一中两人肥城太西中学三人 金城山中学两人肥城六中一人,新泰中学一人。
2104泰教育(升学规划) 00:16查看AI文稿AI文稿
00:16查看AI文稿AI文稿试卷分享,高三全科一模山东省泰安市二零二六届高三一轮检测泰安一模试卷及答案视频时长有限,展示的是数学学科部分资料,如有需要全部学科试卷加答案的,可以微长来取,整理不易。
 01:56查看AI文稿AI文稿
01:56查看AI文稿AI文稿好,第四题,一个很常规的动物定律,对吧?告诉我们返回底端时出出动能是一百八,返回底端动能九十,对吧?那这个动能的损失显然就是摩擦做做了复工嘛,在这个来回的过程当中,对吧?所以说我们就可以对整个过程开做动物定律, 对吧?首先我们先明确上去又回来,对吧?它的动能的损失得是一 k 就是 什么,哎,两次模态做的功,对吧?那我直接写个二倍的 f 乘上 x, 假设上去的距离是 x, 这可行吧,对吧?然后它就是九十, 所以说光上去的话就损失四十五,对吧?然后呢,那都上去的话,那上到最高点,我动能肯定是零嘛,对不对?所以说我上到最高点,动能的损失有四十五来最摩擦,那剩下一百三十五 显然就重力做的复工嘛,对不对?所以说,显然那 f x 等于四十五圈, m g 乘上 h, 对 吧?那我不写 h, 我 写个什么呢?哎, sin theta 乘 x, 那 我就当成重力在下半分里做负功,对吧?然后也同样往上走 x 距离它就等于一百三十五 g, 这可行吧,对吧?就这,所以由此可知,显然小 f 是 不等于三分之一的 m g 乘 cos theta 啊,对吧?那小 f 就是 m g 乘 cos theta 嘛,对不对?所以说,显然 是吧,就剩它了。所以说,我们化简一下的话,显然可以得到 mu 等于 i 三分之一的 tan theta, 对 吧?那 theta 三十度,对吧? tan theta 三分之根号三,所以说乘三分之一即为九分之根号三,所以说,显然二 b 是 对的。哎,这是第四题啊,也很简单,其实啊,就这。
42小彤彤家的大白 11:08查看AI文稿AI文稿
11:08查看AI文稿AI文稿好,第十八题,这个题其实也蛮常规的哈。首先上来第一问,给了我们一个带,传送带,对吧?啊?这个传送带速度是这个 两米要来,是吧?一米要,对吧?然后呢?上来速度是三米要,对吧?所以说他一上来之后要怎么样?是不是显示要减速的,对吧?就这个物块的速度比传送带要快,所以他受到向后的摩擦,所以要减速,然后就问题就来了,这就上上来就是我们传送带第一个问题,比笔记第十页长度是否足够的, 对吧?你有可能是什么?一直减速,对吧?哎,有可能是先减后匀,对不对?就是船载如果足够长,那你就先减后匀,如果不够长就一直减速,对吧?所以说这个地方我们怎么办?那我得先验证呗。上来就是,对吧?所以说运动情况不确定,我得假设,然后加速 a 显示没有,这 一个是两秒秒,假设的话是按照假设成立的情况去假设,对吧?你可以假设他一直减速,减速印也没有 啊,不是一一直减速,减速走上这个,呃,距离 l 之后,你算下速度大,如果它的速度小于传载速度线,是不不成立的,大于的话就成立,对吧?你也可以假设它能跟传载公速, 对吧?就是。然后你就算一下它要走多远,如果这个距离小于 l, 那 就是先减后运,如果大于 l 的 话,显然它不成立,对吧?就这东西,所以说这个地方你在盐贩子上稍微算一下,我就发现它是没法供速的,对吧?它是会减到两秒就散了,对吧?所以说你你在卷上就这么想了,哎,假设不供速, 好吧,我们假设这个数叫 v 二吧,行吧。哎,那么显然减速,那 v 一 方减 v 二方等于二 a l, 对 吧?你把数带进去了,所以说你算这个 v 二等于两倍 就完事了,对吧?所以说,由此,那我们算压缩量吧,对吧?有时候我撞弹簧的时候,我动能是什么二分之 m v 二方,对吧?然后呢,在它为什么它就被消耗完了?被谁消耗完了?摩擦作用和弹簧弹力作用,对吧?所以说摩擦作用显然是 mu m j 乘上 x 啊最大,对吧?然后再加上什么二分之一的 k 方,对吧?然后把我的动能消耗完二分之一 m v 二方,是不是这样就可以了,对吧?所以说你稍微一解算下来,这个最大是三分之一米就完事了,这是第一个的结果。 好,第二位,这也是一个常规的问题啊,就是,呃,是一个动量守恒的一个什么这个轨道类的模型,对吧? 实际上呢,就是我们所在笔记上所讲这种情况,二十六笔记二十六页上,哎,这种轨道类的情况就这啊。首先呢,我们先要明确,就是在他这样一个轨道情况下,这个小 m 跟大 m 之间的一个相对运动是圆周运动, 那就是小 m 相对大 m 的 速度是始终沿这个圆弧牵线的,但由于大 m 是 有水平向方向速度的,对吧?所以导致小 m 的 实际速度绝对把这个水平速叠加上,对吧?比如说我们在这里讲的这个最高点的事问题,对吧?我说了,小 m 相对大 m 的 速度是竖直向上的, 对吧?哎,在这个最高点飞出的时候,小 m 相对 m 速度数值向上,对吧?而此时大 m 由于有水平方速度,对吧?所以说小 m 跟它水平速度一样,因为数值向上吧,小 m 相对 m 速度,数值向上,对吧?所以说我们把相对的速度叠加上大 m 速度之后,就得到了小 m 的 实际速度 啊,就这么一个东西,对吧?我们就可以用这种方式来求,所以说在这里也是一样的,在这个题当中也是这样来求的,哈,对吧?我们就可以用这种方式来求,所以说在这里也是一样来求的哈,对吧?我们就可以用这种方式来求。横吗? 显示不守恒,为什么?他说水平方动量守恒,数值方不守恒,对不对?一定注意,这是陷阱啊,就是选择题,一旦问你动量守恒的时候,第一反应是是不是数值方不守恒啊?就是,所以说,显然,那我们说在这个 b 点飞出的时候, 小 m 相对大 m 速度是朝着,对吧?斜向上六十度,对不对?但是呢,这个题又说了什么?小 m 在 最高点是以什么与水方乘三十度加点飞出的, 它大概是这样,对吧?与水方向成三十度,所以我们简单画上,画起这三十,这三十,这也是三十,对不对?就这么往下,然后呢,在当这个小 m 出去之后,它显示做斜抛嘛,对吧?斜抛上去,对吧?然后斜抛上去的时候,它速度是 v 一 三也没有,对吧?也就说意意味着小 m 的 时运动速度,它的水平方分速度,其就是个 v 一, 对吧?它等于三,没有,对吧?所以说,从这个构图上来看的话,显然 我们是不是就能得到 v y 是 多少啊,对吧?这角三度,所以说 v y 显然是根三,密密麻麻, 对吧?然后就我,我接着要说重点了,显然是叠加之后得到结果,对不对?就这,所以说这是相对速度,对吧?叠加上雾化的速度之后就是这个大 m 速度之后就等于这个雾化实际速度,对吧?所以说,显然,那我们只要知道它 是不就知道了大 m 速度,对吧?所以说从这一小块实际上什么,实际上是一个这个应用, 对不对?所以说选水平方向上这个相对的水平方向相对速度一米秒,对吧?叠加上物块的什么大 m 的 两米为秒,所以我写 v 三等于两米秒,所以就变成了这个水平方的 v 一 三为秒, 是吧?所以说由此我们就可以得到大 m 水平速度在脱离瞬间是两米秒,所以说,那简单一写哈,这个 v 一 是根三米为秒, v y 啊三啊三米秒。写错了, v y 是 根三, v e 等于三米秒, v y 等于 根,三米为秒,对吧?然后呢,水平方向的 dx 等于 e 为秒,然后大 m 的 速度 v 三啊 v 二啊 v 三 v 三,刚才用过 v 二了, v 三就等于两秒, 嗯,水平方向速相减一下就可以了,对吧?所以说我们对水平方向做动量,动量守恒,所以说显然有小 mv 零,等于后来的小 mv 一 加大 mv 三,对吧?所以由此可知 v 零等于 是没有,对吧?然后这个系统既能是守恒的,对吧?所以说显然出动能二分之一的小微零方,对吧?然后呢,就等于是什么?当然你也可以用碰撞来做啊,都行,就类类碰撞来做都可以啊,那他显就等于这个系统的什么默契性能,对吧?那默契性能的话,显应有 mg 二分之 r, 对 吧?或者说重力做负功,对吧?因为它上升了二分之 r 的 距离嘛,对吧?从这脱离的时候,是吧?所以说等于 mg 乘二分之 r 再加上什么系统默认的二分之一的小 m, 注意小 m 的 速度是什么?我们是给用这个, 这才实际速度,对不对?哎,这个实际速度,实际上什么是这个?二根三,对吧?啊,不对啊,四,四,对吧?就这,这个是其实是四,哎,不对啊,是二根三,是二根三,对,这,这,这个段是二,对吧?这这段是跟三,所以说这段是二根三, 当然了,你也可以直接写个他的速度,平方应该为一方加为外方,对吧?哎,实际上就是这个是 v 几来 v 三,对吧?哎, v 三的方, 对吧?就可以了,所以说,显然你这个 r 求出来就等于零点二米就可以了,对吧?关键点就是我们前面这个速度是怎么利用这个题目条件把它给给给给处理出来的,对吧?就这啊, 好,第三问啊,未移,对吧?那这个也没什么说,还是维元法。就是啊,就是水平方向上显他们有个相对位移,对吧?就这个小 m 比大 m 水平上是不是多走了一个什么?是不是二分之根三 r, 对不对?我们这有 v 一 叉了,有相当于 v 一 了,所以啊,那我们如果还能有个别的东西,是不就能算了,对吧?而且他这里给了一个什么?给了一个时间,那这个时间怎么用?很简单,我们考虑归元法。嗯, 这个也不是什么第一次见的东西了,所以我就直接说了啊,所以说我们首先先明确水平方向上是应该始终满足向量等于向量 v 一 加大向量 v 三,这个式子横乘力,对吧? 这两个速度就是在某时刻他们两个顺水循环顺人速度,对吧?就这啊。然后我们取一段时间,几段时间得是 t 一, 在等号左两边同城,这个得是 t 一 的话,那么显然得到选 mv 零乘得是 t 一, 等于选 v 一 乘得是 t 一, 加大 mv 三乘 t 一, 对吧?然后呢,前面不动哈,这个速度跟他没法乘,因为这这个本身并不是一个实际的,就是一个正在变的一个实际的物体的运动速度,所以你他俩乘起来并不会是一个位移去,对不对?所以说我前面不动啊,所以小 v 零乘上 t 一 等于小 m 未一乘的是 t 一, 显就在这一小段时间之内,因为这个是实际的小 m 的 速度,所以就是他们水立方的位置 x 一 看见吧,然后再加上大 m, 那 x, 它俩相乘就是大 m 旋转的位置,我们写 s 一 撇,可行吧,对吧?然后呢,相相应的,我们再乘上时间的 t 二的话, 对吧?然后写的 t 是 x 的 一撇吧,啊,都在的,然后再乘上的 t 二啊显,这样式子可以列出无数个,对吧? v 零乘上的 t 二等于 m 的 x 二,再加上大 m 的 x 二撇, 是吧?所以说这样设定了无数个之后,我们就把它全加起来嘛,对吧?所以前面这个公因子设为 mv 零,对吧?所有的时间全部累积起来,就是我们已知的时间 t, 对 吧?那这个呢?等于什么?小 m, 那 这个就是什么小 m 水平方的微移,对吧?我们可以写个 x x 小 m 吧,对吧?啊?然后再加上这个呢?是不是加起来就大 m 的 微移了,对吧?水平方微移就大 m 小 m 啊, 可以吧,就这么东西啊。所以说为零乘的是 t 啊,为零乘 t, 这个显然是可以算的,为零是已知量,对吧? m 什么都是已知量,对吧?所以这个式你化简一下,它就会变成 六分之根三等于 x m 加上二分之一的 x r m, 对 吧?而我们还知道它们俩为一叉,对吧?它俩为一叉。什么?是不是 x x m 减去 x 二 m 循环位一等于二分之根三 r r 是 已经知道的东西了,对不对?所以说我们做个叉的话,它应该等于十分之根号三, 对吧?所以说最后这两个式连立,我们就可以得到大 m 的 位一 x 大 m 应该等于四十五分之二根三米 就完事了。哎,就是个第三位啊,非常正常的一个常规的微安法,哎,已知它们的一个 就是给你的时间,给你时间是让你求他们两个一个核关系,对吧?然后你通过前面的题目条件能知道他们一个差关系,所以俩是连力就完事了。就这啊,这是第十八题,还是并不算难哈,肯定不算难的啊。
 02:08查看AI文稿AI文稿
02:08查看AI文稿AI文稿好,第二题,核反应,那么这个核反应的话,就是我们笔记六十二页上,首先我们先明确一点,核反应所释放能量我们可以用智能方式来进行计算,对吧?就是这个释放能量 e 应该等于亏损的质量乘上光速平方,对吧?所以 e 等于等于 m c 方, 是吧?而这个释放能量也可以通过结合能来进行计算。那么我们先解释下什么叫结合能,很简单,就是结合成核子,结合成原子核,所谓释放能量,所以说我们要这么去理解原子核, 我们将原子核拆分成核子,它会吸收能量,这些核子重新聚结合则会释放能量,所以说整个的一个核反应竟然是释放能量的,那就说明什么?说明我的反应物 全部拆开,所吸收的能量小于哎,再重新组合成生成物会释放能量,对吧?组成生成物要释放,拆开反应物要要吸收,对吧?所以说释放的减去吸收的就是我们净释放的能量,也就是整个合反应释放能量, 对吧?所以说我们的计算方式是生成物的结合能,减反应物的结合能。换句话说,各位同学一定要记得,生成物的总结合能是大于反应物总结合能的,就这么东西,好吧,所以说如果是比结合能的话,我们想算结合能,就得用比结合能乘和的数了,对吧?所以说显在这个题当中, 我们就这么来算的,首先生成物啊,首先我先说释放能量叫得 m c 方,对吧?它就应该等于生成物的结合能, 那生成无限是里七,对吧?那他的结比结合能是 e 二,所以说七倍的 e 二,这是里的结合能,然后呢?再加上 high 的 结合能,对吧?阿尔法粒子 加上它的结合能叫 e r, 看见吧?他这个问题是结合能不是比结合能,所以说不用除以四哈就是。不不,不用说,前面写个四哈就是,然后呢?再减去什么?减去朋朋十的结合能, 对吧?这是拆开的,对吧?所以减去十倍的 e 一 就可以了。所以说你算完之后选第一题是四 d 啊,第二题是四 d, 就 这么个东西啊,是很简单。
34小彤彤家的大白 10:30查看AI文稿AI文稿
10:30查看AI文稿AI文稿好,十二题一个比较常,算是一个比较常规的配速法吧?算,是啊,这个 c 和 d 是 要用配速法做的, 然后这个 a 和 b 比较比较简单,对吧?我们从上边滑下来,对吧?滑下来之后呢,进去以后电场力的作用导致我们在里边加速, 那么速度越快,我们受到向上的洛伦兹力越大,那当我们的洛伦兹力等于重力的时候,是不是我们就该起飞了,对吧?所以说这就是在水平面上,我们就算一下从进去到重力,当这个洛伦兹力达到重力的时候,这个过程有多长时间就可以了,对吧? 所以说我们就需要先算一下进来的速度档,对吧?所以说显然从上面下来重了,做工嘛,对吧?所以说显然一上来 m g r 等于二分之一 m 归零方,是吧?所以说我算来归零等于根下二 g r, 哎,这一上来,然后我们再去算,当我的落地点重力的话,那显然应该有 q v b 等于 m j, 对 吧?所以我们要去求这个 v 是 多少,对吧?你算完这个 v, 它就等于四倍的根二,这样, 对吧?然后呢,在这个过程当中,显然电场力都是它加速的,对不对?所以说显然我们可以给个度量定理,对吧?哎, q e 乘上十点 t 等于 mv 减去 mv 零, 是吧?所以说我们把数据代入的话,显然我就可以得到这个时间 t 就 等于四倍的根下 r b 小 于 t, 就 这,所以说显然上来 a 是 对的,就这来事很简单哈。 这个,这个是怎么来的?我说一下,就是你没有出租座,哎,这这个这个,你就你,你直接把这个微就是这,这边不要出租座,你算下来就是他。换句话说就是啊,一个一个比较 简单的陷阱啊,就是从零开始出发,然后那这样这个时间是他,就这么我想一个比较简单的陷阱,好, c 和 d 最大速度, 那我们起飞了以后显然还是要往前走的吧,对不对?往前走,往前走,同时重力这样做正功,重力做副功,对吧?所以说肯定有某个位置是速度有最大,是吧?然后那我们此时做啥?这样的,首先我们先看他接下来做什么运动啊?肯定是配速法,对吧?为什么是配速法呢?很简单。 嗯,那我们笔记五十页上有详细的表述,哎,就这么简单,你碰见 e b 贡献的时候,他大概率是个悬镜,哎, e b 垂直的时候正常就是配速了。那你说老师这是一开始他也不是配速,他是匀速直线,为什么?但是没起来,对不对? 他还没有开始做曲线运动,对吧?一旦他开始做上复杂的曲线运动时候, 哎,他就会是一个平面或立体的一个曲线,对吧?那么如果是平面曲线就是 e b 垂直情况,那就用配速法做就可以了,对吧?所以配速法的核心就是我们要垂直于横力去配速, 对吧?因为我们需要一个速度去产生落轮之力,去跟我们已知的横力去平衡, 对吧?然后呢,这个地方你做合成也行,做分解也行哈,就是如果是初学阶段的话,你可以用合成来做,如果你已经很熟练,你可以用分解来做,我可以演示一下哈。什么意思?就是垂直于横力配速,然后我们分别得到一个匀速直线和匀速圆周就可以了。 好简单演示一下啊, 好,首先我们先明确我们受到什么向下的重力 m j。 呃,啊,画一下吧,然后我挑个别地方画吧。首先我们先收到向下中的 m v, 然后呢,我们有水平向电场力,为什么我先把这个呢?我就,我,因为我说的是垂垂横力配速嘛,对不对?所以我先把所有的横力找出来,对吧?这是我们所有所有的两个横力,这是 q e 哈, q e 等于四分之三的 m v 啊,写上写在这吧,所以说这两个都是横力,所以说怎么办?先把它合成,哎,你先得到一个 合力,显然这个合力是四分之五的 mg, 这里是三十七度,对不对?我写个 set 啊, set 有 三十七度, 对吧? so, 所以 说,那我们是不是垂直于这个四分之五 mg 来进行配速就可以了,对吧?所以说在最开始的时候我们显然拥有一个。嗯,我先画条,画两条辅助线啊, 哎,斜向下三十七度的一个四分之五的 m g 的 横力,然后我们有一个水平线的出速度 v, 这个 v 等于四倍的根下二 g r, 是吧?好,那我怎么配速?很简单,我现在需要一个跟它等大反向的力,由一个我们需要的一个速度产生洛恩兹力来平衡它,对吧?所以说我们现在需要一个反向的四分之五 m j, 所以 说由叉状磁场可知,显然这个速度是不是应该朝右上去,对吧? 应该朝右上,至于多大现在不好说,但这个角肯定是三十七,对吧?哎,我先写个 c 塔啊,那这个速度大呢?那我就得算一下,对吧?垂垂横力配送吗?对吧?这个四分之五 m 力就是我们速度给的,对吧?我们假设这个速度为 v 一, 那么此时显然也有 q v 一 b 等于四分之五的 mg, 对 吧?假设有个桥右上的 v 一, 对吧?那这个 v 一 呢?它就会等于五倍的根二,这样,对吧?所以说你往右上的给的这个速度是 五倍的根下二,这样,哎,所以你看这不巧了吗?对吧?这是三十七度,对吧?所以说我们将 v 进行分解,分解成一个 v 一 的话,那另外一个分速度显然就是向下的,这个 v 二 就成这样了,对不对?那么这个三十七度角加持下,显然这个 v 二它就是什么,是不是三倍的根下二,这样 对不对?所以接下来是这个 v 二做匀速圆周,其实现在已经不用画,无所谓了,这个是做匀速圆周的,这个是接下来做匀速直线的,对不对?然后呢,那匀速圆周的话, 显然它受的力是水平向向右的,对吧?随时可以转圈,对吧?那我们要问最大速度,请各位同学一定要谨记。 我们对于配速法的结果上来说的话,不管是哪一种,像这是一种比较简单,这种比较复杂的哈,不管怎么说,就是你这个物体实际运动速度,实际上就是你匀速直线和匀速圆周这两个速度大小的合成结果, 因为匀速直线的速度是恒定的,对吧?方向大都不变,然后匀速圆周呢,它的方向是任意改变,所以就成了一个 v 跟 v 撇合成角度任取,那他取的范围什么?是不是应该是他俩的大于等于他俩之差,小于等于他俩之和,是不是?就这,所以说显啊,这个地方最大速度是不就直接就他俩的和就可以了,对吧?所以就是八倍的根下二,这样, 所以说显然是 d 是 对的。就这,这是我们按照分解来做,那么如果按照合成来做怎么做啊?然后如果你以前不太会这种方法,那你就可以天天接下来个思路啊,可能更容易理解啊。好,我们还是画一下辅助线啊, 其实跟分解的做法是一样的,非常类似啊,好,我们有一个朝着的横力叫四分之五的 m j, 还是跟刚才一样的起手啊?然后我们有一个水平向右的 v 等于四倍的根下这样,那根下二,这样啊,写错了,根下二,这样啊,根下二,这样。好,那一上来我们怎么配速?很简单,我们上来直接给 两个分两个速度,垂直于横力给两个速度,然后这两个速度我们都管,它叫 v 一, 看见吧。啊,就是你不用管别的,上来先垂直给给两个速度,这个点显示 c 塔,对吧?那么这个速度多大呢?它是有讲究的,显然这个速度所产生洛伦兹力要跟它平衡,对不对?所以说我们跟刚才一样的似的, q 为一 b 等于四分之二,这样, 对吧?所以说你上来得到了 v 一 大小, 好,那它就负责产生一个这样的洛伦兹力,对吧?哎, q v 一 b 去跟这个四分之五 m b 去平衡,所以它开始做匀速直线,对吧?那另一个速度干什么?很简单,另一个速度拿它去跟初速度进行合成, 合成到得到一个核速度,然后让那个核速度去做匀速圆周就可以了,所以在这个点三十七度加时下,这是四,这是五,对吧?你合成结果显示竖向下的,就这,所以说它显示 v 二等于三倍的根下二,这样, 就这样,所以说,哎,你得到了 v 一 和 v 二,一个匀速圆周和一个匀速直线,哎,一样的结果,就这啊,那为什么这样来去讲这个事呢?很简单哈,就是你如果是初学阶段的话,像刚才这种分解,这个速度你可能是凑不出来的, 然后凑出它来之后另一个速度你不好凑,就像他说你去分解,你可能在不熟练情况下,你一时一下子想不到,所以说啊,我就,我就说一种比较简单的啊,或者无脑的方式,就是你上来先找横力,找完横力之后,咔,直接给俩速度,这个速度给多大? 哎,你心里有数,对吧?你可以算,算完之后好了这两个速度,你看看哪个是做匀速直线的好,这个做匀速直线,对吧?好,匀速直线这个没了之后还剩两个数量,两个数八给合成,合成之后这就那个匀速圆周了, 这样的过程就不需要你去做,你可以跳过那个分解,就这样,这样的话可能对于初学者比较友好一些,如果你熟练的话,可能对于初学者比较友好一些的思路,其实是啊啊,这是第十二题。
 12:49查看AI文稿AI文稿
12:49查看AI文稿AI文稿好,我们来说第十七题,这个题其实是个常规题哈,好,首先第一问问我们这个 b 棒到达底端时的一个电耗量,那么考虑电耗量的话, 显然我们可以啊,写错, q 等于 deffy 比 r 总, 那我们可以先商量先考虑这个式子,对吧?这个就是我们在单杆模型当中讲的五十三页啊,单杆模型当中讲的,对吧?通过什么什么电和量,对吧?那 q 显然应该等于 a 乘时间 t 嘛?但由于这个电流是变的,对吧?所以说我们可以用平均来乘时间,对吧?所以说那平均电流的话,可以等于 d r 比 d r t 嘛? 所以德尔替约调就是德尔赛比亚走,对吧?这个我们可以用这种单杆来考虑,这种双杆的也可以,线框的也可以,对吧?就像这个,这个我一开始的时候相当于是个线框吗?对吧?这两个杆之间 相当于是被强行锁定的,对吧?所以说相当于线框。然后呢,在一磁场当中,它的磁动量是逐渐,它的磁感强度是逐渐发生改变的,所以说它实际上是一个感声电动式,哎,这个在过第一段时候是没有动风电动式的,对吧?所以说那此时那事就简单了, 首先有了感声电动式之后,对吧?这个 b 一 逐渐变大,对吧?大拇指垂直垂直斜面向下,对吧?然后四指方向是电流方向,所以说电流方向 是这样转的,对吧?然后那,那么此时我们显然可以分析一下他们两个边所受的安培力,那我知道安培力多大反向了,对吧?所以说,显然你往下去的过程实际上是什么?实际上就只有重力的向下分力给我们提供加速度,让我们往下做什么?匀加速直线, 对吧?就这么个样子,是吧?哎, ip 打反向,所以说不用看了,所以说,显然我们一我们往下加速这个过程,我们可以得到 a 等于这一乘三 c, 也就是六米二毫米, 是吧?然后最终我们加加上一个速度,对吧?这个 b 棒到了,达到了速度 v 二,是吧?所以说,显然 啊, v 一 v 一 啊,达到了速度 v 一, 对吧? v 一 是这个两米一秒,对吧?所以说显然,那我知道 v 一 等于 a 乘时间 t 一 嘛,然后第一段时间 t 一, 对吧?所以由此可知这段时间 t 一 等于 三分之一秒,是吧?然后所以说我们往下去的过程中,咱的这个 f 一, 对吧,显然它可以等于呃九 t 一 的方,对吧?也就是一特斯了, 所以说按照我们上面的公式啊, q 等于得这反比上 r 总 r 总的话,就是它 俩串联二 r, 是 吧?所以说显然应该等于最终的结果,初初时是零,对吧?最终结果是 b 一, 所以 b 一 直接乘 s 吧,对吧? s 的 话就是一一平方米,对吧?就是 l 乘 d, 是 吧?然后比上二 r, 所以 算完 q 等于一库仑就完事了啊,是很简单很常规。其实啊, 第二个呃水平导轨进入右边磁场,那他进入,他一旦进入右边磁场就出现一个问题了,他这个地方 n q 是 绝缘的,对吧?所以说当这个杆分在两边的时候,这个电路中是没有没有电流的, 对吧?就根本就走不起回路来,是不是?所以说就呈现着你走你的,我走我的状态,是吧?所以说,那这既然这样的话,那个 n q 他 没有这个,这个这个 b 杆过了 n q 之后,他不受外力了,所以他要匀速走,对吧?然后呢?这个 a 杆 在这个 n q 斜上方一米的地方,对吧?还距离这个 n q 还有 d 的 距离,对吧?然后他再继续加速走一段呗,对吧?然后这个时候他也不受安培作用, 是不是?哎?你没有闭合回路,对吧?所以说再继续往下再走一段,过了 n q 之后,当他俩都进入水平磁场之后,才会出现一个双杆的一个相互作用,是吧?就这么东西,所以说我们要先考虑的是我们现在这个 a 杆进去看见吧,他得加速走一段走 d 的 距离,对吧?所以说显然我们可以先 考虑重力做功,对吧?所以说 m j 乘上三 c, 我 们可以认为是重力下二分量,对吧? m j 三 c 的 乘上这个距离 d 等于二分之一的 m v 三方,减二分之一的 m v 一 方,那我们假设这个 a 进过 n q 的 时候,速是 v 三, 是吧?嗯,这个 b 过 a q 速是 v 一, 此时这一瞬间这个 pm 就是 个 a 二,也是也是,也是 v 一, 对吧?然后 v 一 走加速走了一米的距离之后变成 v 三,是吧?就这么东西,所以说在这过程中就中了一个,就中了一道功,对吧?所以说我们算算这个 v 三等于 是没有,是吧?然后呢?那我还得算下这段时间,因为在这段时间当中, b 杆是匀速往前走的,对吧?你看这个第三位让我们求距离嘛?对,我,那我得知道知道出使距离多少呗?就是说在 a 杆到达 p q 这到达这个 n q 的 瞬间,这个 b 往前走多远?就是他们两个刚进入水平磁场的时候了, 水平区域磁场是一个出使间距,对吧?所以说我们需要算下这第二段时间,对吧?所以说我们直接这样写, 对于 a 耳来说,现有重力下滑,分力给什么?提供冲量,对吧?哎,冲量改变它动量,所以给动量乘以啊,所以就是 mv 三减 mv 一, 所以说这第二段时间等于三分之一秒,对吧?就是我发现这个出题的人很喜欢三分之一这个数啊。第十八题第一问结果也是三分之一啊,三分之一秒,然后呢?那么此时显然我们就可以 算出来这个这个谁一上来走了多远了,对吧?就是这个 b 杆过了 n q 之后,对吧?在这个 a 杆还没有到 n q 的 这段时间内走了多远,对吧?所以他是匀速,所以说我写 x 还写 x 一 吧, x 一 是不是就可以等于 v 一? 对,他还是以 v 匀速的走了 t 二的时间,对吧?所以说他就走了三分之二米,那这个三分之二米是 ab 杆在水平算当中的一个触矢间距, 然后那接下来是不是就开始这双杆开始相互送了,对吧?我要求九点热,那么在这种情况下我们分,我们发现他实际上就是什么,实际上就是一个动量守恒的模型,对吧?这是我们笔记五十五页讲的, 哎,等长的一个只有出速度但没有外力的一个双杆,对吧?当这个 a 杆也进入磁场之后,他俩开始相互送的时候,他俩都有都有出速度,但是没有外力的情况下,那那,那这个电路 各位团要注意,它是嘚嘚嘚是一等于零的时候,是稳定状态,但这个题也没有给我们稳定状态,因为它最终结果吧,最终结果实际上就是他们两个就是这两杆共速,共速才稳定,但这个题最终也没有给我们共速,换句话说就是这个区域 转笔转掉地上去了啊,嘿嘿啊,这个区域它太短了,所以说还没等到稳定状态就结束了, 就这么个意思啊,所以说,那我们此时首先这个地方还是应该是动,让手横来解就可以,为什么?原因是解的就是这两杆所受的安培力一定是拿反向的,因为他们长度是一样的,电流大小是一样的, b 是 一样的,对不对?然后呢,你别管这两个谁谁大谁小, 对吧?就谁切割产生感势大,他们两个产他们两个,电流在电路当中一定是你来我往的, 对吧?就这,所以说安排一定的大方向就这样,所以说此时动量守恒,那外力使二和为零吗?对不对?所以说此时我们就用动量守恒来处理接下来问题了,对吧?我们知道这个 a 杆最终的速度 是二点五,对吧?二点五的时候从右边出去,对吧?那此时这个 a 杆速度多大?我们假设为 v 四的话,那么我说了,既然动量守恒,显然我们可以得到, 选 v 一 加选 v 三,对吧?这是这个系统出动量等于系统末动量选 v 二加选 v 四, 对吧?所以我们得到 v 四等于三点五米每秒就完事了, 对吧?然后呢,那损失,动损损损失的这个,这个,这个机械能或者产生涡轮热呢?显然就是我们说的啊,这是个类似完全非弹了,对吧?我们再用能量啊写一下就有了这个产热,对不对?还是笔记五十五页这个地方啊。所以说,显然就是 二分之一选 m v 一 方,加二分之一的选 m v 三方,对吧?减去 q 等于二分之一的选 m v 二方,加二分之一选 m v 四方, 对吧?所以说我们算来这个 q 等于一点五圈,第二位就结束了,就这好,第三位,那这个更简单了,问我们后来的距离对不对?所以说这是什么?我们直接用这个, 哎,在这种双杆的一个动量守恒情况下,等长动量守恒情况下,我们对单杆做一个动量定力, 对吧?然后呢,那么不管对谁做都行,因为动量守恒嘛,这两个杆动量动量变化量大小是得大反向的,对不对?所以说安培冲量也得大反向,所以你对谁做得到结果都是一样的哈,所以说安动量变化量等于安培冲量,那安培力的话相当于 i b l 乘三 t, 那 a 的 话等于什么?是不等于感应电平均感电磁场上时间,对吧?平均感电磁场除以电阻,对吧?这是平均感电流,那平均感电磁场应该怎么算呢?在这里好了,就这个, 因为这两个杆速度一大一小嘛,对不对?所以说,而且都是朝一个方向运动,所以说他们两个所产切割所产生感电磁场应该是相减以后才是这个电路的等效感电磁场, 对吧?所以说我们应该什么是 b l v 一, 减去 b l v 二这个样子来算,对吧?所以说当我们给了平均以后,对吧?那么此时就是 b l 什么哎, v 一 减 v 二都是平均,对吧?都是八,然后呢,乘上时针 t 是 不是就变成 v 一 了, 对吧?你可以这么来理解,但你也可以用呃这个 v r 法来理解,也行,都可以啊,我们简单写一下,就说你对单数做到了那里,你就可以得到 这两个杆之间变近或变远了多少,对吧?现在我们也知道出时间就是三分之二了嘛,对吧?所以说他们俩肯定是变近了,对吧?因为这个呃 a 杆速度更大一些,对吧?他是从四减到三点五,对吧?然后呢,这个 b 杆是从二加到二点五,是吧?所以说显然是变近了,对吧? 但是我们对单杆做多少定力哈,显然应有氨氨的冲量, f 氨 八乘十减 t, 对 吧?等于什么?那我们其实对 a 看也看 a 也行,看 b 也行,对吧?因为咱光看是一样的吗?对吧?那为了方便起我们看来看 b, 因为 b 的 b 是 加速的,他的一个这个动量,动量变化量是正的,对吧?所以说用正的好算,对吧?所以说 mv 二减 mv 一, 对吧?这个东西好,然后我们对左侧 f i 乘时间 t, f i 八乘时间 t 已经变形,对吧?所以说就是 i 八 b l 乘 t, 对 吧?然后呢, i 八就可以等于 b l, 那 它们两个本身是什么啊? b l 这个我想我写个呃 v 三减 v 一 吧, 呃,我写 bl 的, 对吧? blv 三是 a 杆切割产生感应式,对吧? blv 一 是 b 杆切割所产生感应式,对吧?然后呢,这两个感应式在电路相反,所以我们要给个相减,对吧?然后它除以总电阻二 r, 这是电流,对吧?电流乘上 bl 乘上实验题,就刚才说的过程,对吧?但是呢,我们既然是加平均数,我们上面也都加平均,当然了,你也可以用微机呃,微元法来写,就这,但是没什么必要啊,其实你这么写表述对了,也产产产,这么产出也是可行的哈,就这我们也接受, 所以说它等于什么呢?那显平均速度长时间之后,那显然就等于 bl, 那 两个平均速度长时间都变成未知了,都变成这两个各自未知了,对吧?那未知相减的时候就变成变近的距离,就是 x, 对 吧?然后乘上 b l 就是 方方 就变成这样了,对吧?所以说这个是是不是就变成了 b 方 l 方得 x 比上二 r 等于一个 m v 二减 m v 一, 对不对?是不是都是已知量了,对吧?所以说显然你算来这个得 x 就 等于九分之四米, 就这,哎变近了九分之四米,所以说,显然它们最终距离 x 二就等于初值减去 x 一 减去这个得 x 啊,就等于三分之二,减九分之四就等于九分之二, 就这,哎,就是个第三问啊,是很常规的一个问题啊,就是我们等长双杆中非常常见的一些问题啊,就这。
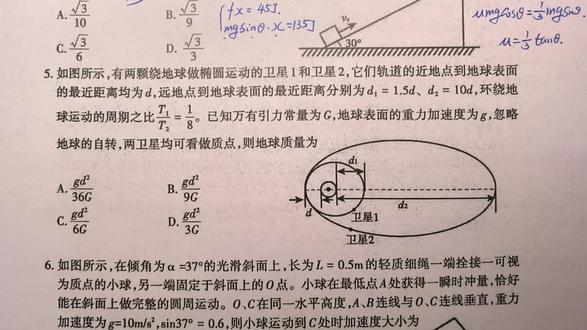 02:26查看AI文稿AI文稿
02:26查看AI文稿AI文稿好,第五题上来先给了我们两个轨道到地表的一个距离,对吧?远远点距离,近点距离,然后呢,告诉我们它们周期之比,所以说你第一反应肯定是开补的参考率,对吧?因为咱只有开补的参考率当中有这种周期之比啊,这种,哎,因为明显给了长轴了嘛,对不对?就这样,所以说,显然 我笔记十八页长,对吧?半长轴三次方之比啊,半长轴三次方比周期 t 平方之比是一个什么定值,对不对?所以说像这个题我们就可以这样来写了,所以说显然一上来的时候我们需要写的东西就是 我们写的稍微靠右一点啊,显然,那我先看这个小的这个椭圆,对吧?他的一个半长轴应该是 d, 对 吧?加上什么?这个 d, 一 d 是 一点五 d 啊, 然后再加什么二 r, 对 吧?加地球半径为 r, 对 吧?然后这是它的长轴,对吧?除以二, 然后它的三四方,这是半长轴三四方,对吧?然后比上 t 的 平方,它的周期是 t 一, 对吧?等于这个 长,这个椭圆,对吧?这个是 d 还是一样的,哎,我们写 d 加上什么?这个 d 二 d 二号是十 d, 对 吧?再加上二 r 啊,除以二啊,忘除二了啊,哎,它的三次方,对吧?然后比上 t 二的平方, 对吧?所以你把式稍微变换一下,你可以得到这么一个,就是十一 d 加上这个二 r 比上二点五 d 加二 r 正好等于四,就这,所以说你算 r 等于六分之一的 d, 就 这,所以说此时,那你让人问地球质量了,我们是不是就可以直接怎么样?是不是就可以黄帝代化了,对吧? 我们可以直接认为地球表面万有引力等于重力,对吧?还在忽略星球自然情况下万有引力等于重力,对吧?所以说我们直接得到什么大 m 的, 这这这 r 方比大 z, 对 吧?就完事了,就黄金代换嘛,写就是,对吧?就这样。所以说显然让我们直接写一下的话,显然那大 m 等于 这样方比大 j, r 也有了代入,对吧?所以说显然 a 是 对的,哎,这地方比三十六大 j 就 这哎,这是第五题啊,其实很简单,就这啊。
30小彤彤家的大白
猜你喜欢
最新视频
- 6906江清嘉








![公益分享解题策略与技巧第一百一十一天:山东省泰安市一模第14题选讲。欢迎关注+转发+点赞+收藏,惠及广大学子[抱拳][抱拳][抱拳]#解题技巧#立体几何#球与圆柱内切#组合体问题](https://p3-pc-sign.douyinpic.com/tos-cn-p-0015/oAXAtcfAGEzaOACAVaBgtkhPzHIgeD1AC0t7aB~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2085771600&x-signature=2z329oH9d3mKDMGqnakVLTby2Wk%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20260207050716805DD761CBC4D8BE932C)
