重庆南开系列几何压轴大题初三
粉丝284获赞1322
相关视频
 01:12查看AI文稿AI文稿
01:12查看AI文稿AI文稿正方形问题,中考特别爱考,一定要重视起来。来看一道重庆中考真题,你可以先看题目思考一下。 我们先从条件出发,这里有 b、 f 为角 a、 b、 e 的 平分线,又有 b、 e 等于 b a, 显然只要我们连接 a、 f 便有三角形 b、 f 于三角形 b、 e、 f 全等。 很多时候,几何题的解析思路少不了几何直观。我们看到图中三角形 a、 f、 c 非常像直角三角形,如果三角形 a、 f、 c 为直角,三角形 o 又是斜边的中点,直接利用斜中半即可解决问题。再结合我们刚才证明的全等,我们只需要证明角 b、 f、 e 等于四十五度, 即可证明角 a、 f、 c 等于九十度。因为题目中角度比较多,线也比较多,所以我们尝试用设微之数的方法来表示角度。 我们设角二等于 x 度,那么角 e、 b、 c 就 等于九十度,减去 x 度。因为 b、 e 等于 b、 a, 所以 b、 e 也等于 b、 c、 e 得角 b、 e、 c 等于四十五度。加 x 度,再利用三角形的内外角关系,就可以求得角 b、 f 一 等于四十五度。 这样我们就可以证明三角形 f、 c 为直角三角形,再利用斜中半即可求得 f 二的长度。你学会了吗?
44中考数学提分王 12:35查看AI文稿AI文稿
12:35查看AI文稿AI文稿讲一下最新的五中稀缺的这个期末考试的第十题啊,我们来看一下题目。首先审题, c 呢等于 c, b 等于二。标一下二二角 a, c、 b 呢等于九十度,所以这样能得到一个等腰直角三角形 a、 c、 b, 因此 a、 b 呢等于二倍。根号二 点 d 呢,在 b、 c 上运动, d 是 动点 d。 在 运动的过程中呢,以 a、 d 为边,做一个正方形, 做一个正方形,过点 f, 再做 f, g 呢,垂直于 c 的 延长线,交它呢于点 g, 然后把 f、 b 呢给它连起来啊,交这个 d, e 呢于点 m, 这个 d, e 呢又跟这个 a、 b 呢交于点 n。 问,下列说法错误的是, 那这一题很显然它是一个怎么样反照这个二五年咱们的这个中考题出的一道这个压轴,对吧?我们这二五年的那个背景的话是一个刮豆模型,那这题依然还是一个呃,刮豆模型。所以这一题的话,就需要大家对刮豆模型呢有一个非常熟练的一个了解。 好,我们来看一下啊,这个刮动模型呢,我们就先不在这里面介绍了,有兴趣的同学。嗯,可以看我以前录的这个视频。我们来看一下这个刮动模型的话。呃,很显然这个点 d 呢是主动点, 点 e 呢是从动点好光度模型满足什么呢?就是主动点到定点的距离跟从动点到定点的距离比是一个定值。那这题很显然, a、 e 比上 a、 d, 就 这有个距离比, 这个距离比很显然等于根号二是一个定值。还有一个就是夹角的这个夹角,比如说主动点 和定点的连线,从动点和定点的连线,你看,以定点为顶点组成的这样的一个夹角,那这个夹角呢?也得是一个定角,那这题很显然它是一个四十五度,有了这两个条件,它才符合我们的这个刮动模型。 那刮动模型的话,熟悉的同学应该知道,就是主动点的轨迹它是一致的。现在主动点的轨迹呢, 是在一条直线啊,或者说他这是直线上面的一条线段,那么我点 e 呢?他应该也是直线上的一条线段,对吧?那么所以这样的话,我们就可以把从动点的轨迹给他,干嘛给他确定,我们要确定这个从动点的轨迹, 那从动点的轨迹呢?如何去确定呢?方法呢?有很多。那这题比较特殊,我们可以通过主动点的特殊位置去找从动点的特殊位置。 大家来看一下 d 点在特殊的位置时候,能推 e 点的这个特殊的位置,我们就把 d 放在哪个特殊位置,你比如说 d 可以 在 这个 c 的 时候,对吧?那如果 d 跟 c 重合,此时 a d 是, 是这个对不对?那很显然,那我的这个 d e 呢?是不是就呃等于这个 c b, 所以 这个当地在 c 的 时候,那 e 呢?是不是在这个地方?这帮我可以标个 e, 对 吧?好,那这时候我们再找 d 的 一个特殊位置, 那显然我们可以找当 d 在 b 点的时候,你是不是以 a d 为边?是不是再向外面再做一个?等腰直角三角形的时候,或者在外面再做一个这个,呃,正方形的时候,给它擦一下,那此时这个正方形画出来了,那刚好 应该是长这个样子啊,那刚好应该是长这个样子啊,那差不多呢,嗯, 在这啊,这个地方我图就不要画的特别准了啊,那很显然,那这是一几啊?这是一二,你看这三个点刚好在一条线上面,一一一二一三,我们刚才知道这个从动点的轨迹是一条直线,对吧?其实我只要找这条直线上面的两个特殊的点,就能把这条直线给它,缺什么给它基本确定了啊。 好,那这样的话,我们的一点的轨迹呢,就全部怎么样解决了?把这个图给它擦掉,五官的图都给它擦掉啊, 那这个一二的这个点的坐标呢,也比较特殊,也比较特殊,那我们来看一下啊,因为这个角是四十五度,这个角呢也是这个,呃,四十五度,所以这个三角形,这个三角形相当于就是一个等腰直角,是吗?三角形啊, ok, 那 我们现在把这条线呢再给它延长一点点,那整个 e 呢?就在这条直线上面干嘛动啊?这上面动。 好,嗯,我们来看一下啊, a 选项,他是说了当这个点 d 在 直线 bc 上面运动的时候,也就是说 a 选项有一个关键词,他把地点的这个运动的一个范围,从刚开始的这个边上面运动扩展到了这个直线上面运动, 所以现在这个 e 点的轨迹也是在整个直线上面动,而 a 选项让我们求 a e 加 c e 的 最小值,那很显然 a 选项求的是 a e 加上 c e, a e 加上 c e 的 话,它的一个是线段之和的最什么值?最小值,因此的话,那 a 选项很显然是一个将军印什么印码,而且是两定一动, 你看啊, a e 加上 c e 的 这个最小值,那很想我是不是做一下对称就可以了啊?那我就把 c 点关于它对称一下,我们把图给它标一下。 好,咱们把这个 c 呢给它对称过来,用个绿色的吧,对称过来,好,对称到这个地方,这边标一个 c e 撇, 那此时的话,我们的这个 c e 是 不是就变成了 c 撇 e, 然后直接连上 a c e 撇是不就可以了?也就是说,此时 a e 加上 c e 的 最小值,是不就等于 a c e 撇, a e 加上 c e 的 最小值,等于 a c e 撇,我们怎么去计算?那很显然我们还是要去。呃,添加辅助线,把它构造成一个直角三角形,我可以过 c 呢,往这边再做一条垂线啊, 这方我标个点 m 点 q 吧。 ok, 那 么现在我们开始一个计算,呃,咱们知道这个角呢,可能说是四十五度,那这个角呢,也是四十五度,所以 三角形这个地方呢,这个三角形它是一个等腰直角三角形,这条边呢是二,因此的话,那这个,呃,这条边的长度呢,就等于根号二。对称过来,这个长度也是根号二,这个方是垂直的,所以我们的 c c 一 撇呢,等于二倍根号二,是不等于二倍根号二, 而这个角呢等于四十五度,这个角呢也等于四十五度,所以我们的 c 一 撇 q, c 呢,它是一个等腰直角三角形,因此这条边呢, c 一 撇 q 等于二, c q 呢也等于二,所以我们再用勾股定顶,就能把它长度呢给它算出来了啊。那此时很简单,等于根号下, 应该是二的平方,再加上四的平方,所以答案呢,应该等于二倍杠五,所以这题的最小值呢,应该等于二倍杠五,并不是等于二倍根号二加二。如果你选了这个答案,你是估计没有看到这个关键词,它是在直线上面运动。好,这是 a 选项,所以当然呢,这题呢,就直接选 a 就 可以了。 这个和我们二五年的那个安徽中考题,他的那个第十题的压轴题的答案呢,也是 a 选项,如此一个类,一个意思啊,一个意思,但是他也是,呃,有一个审题的一个关键点。好,那这样的话,我们 a 选项呢,就不在这方继续讲了,继续我们看 b 选项, b 选项的话,它点 d 在 边 bc 上运动的时候,问我们正方形 a、 d, e、 f 面积的最大值,那 b 选项很简单, 这个正方形是不是等于 a d 的 平方,所以 a d 最大的时候呢,它整个面积就最大。那很想这个 a、 d 是 不是有一个直线形的距离,就是一个线段,那它距离最大的时候,肯定到 a b 的 时候是最大,所以那个 b 选项它是对的啊,所以这个 s 的 最大值呢,刚好等于二倍根号二括号的平方等于八。 c 呢?我们再看 c, c 是 点 d 在 这条边上运动的时候, b m 的 这个最大值是二分之一,我们知道这个地方是个垂直,所以这个图里面会形成一个一线三等角, 这有个一线三等角,这种题目在做一线三等角的题目的时候应该接触过,对吧?我要求一下 b m 的 这个最大值,那这个地方呢,我们就可以几何转代数啊,几何转代数, 那这条边呢,是二,我们可以设个圆就可以了。设这条边是 x, 那 这条边呢,等于二减 x, 把 b m 呢设成 y, 我 们知道这方有一个一线三角的相似,那熟知一线三角相似的乘积式的结论的同学,这方就可以直接写了啊, 或者你把比例式列出来,那我们直接写乘积式,应该两个 y 等于 x 乘上二减 x, 那 这方把 y 呢写出来,应该等于二分之一, 这个负的二分之一 x 的 平方再加上 x 配方就可以了。那就是负的二分之一 x 的 这个平方再减二, x 再加一,再减一,等于负的二分之一 x 减一,括号的平方再加上二分之一。所以 当这个 x 等于几时?等于一时,它的最大值呢?等于二分之一一,刚好呢,在这个取值范围上面,对吧?好,所以 c 答案呢,也是对的啊。这题比较难的是这个 d 选项啊,像有很多同学当时呢可能没有办法很好的处理这个 d 选项, d 选项呢,是一个模型, 这模型大家可以学一学啊,就是目前像咱们安徽的话,考的不是那么多啊,不是那么多,它是一个斜大于直的模型。斜大于等于直来讲一下啊,那 这个三角形是一个直角三角形,那这种题目呢,因为我们要求 a n, a n 刚好是这个直角三角形的斜边,对吧?我们遇到直角三角形的斜边,我们可以考虑取一下 a n 的 中点,取 a n 中点 o, 我 们取一下它的中点 o。 啊,这个地方的话,嗯,图不一定很准啊,就差不多这是点 o。 好, 这是它的中点,那显然的话, o d 是 不就是这个?呃, o n 的 这个 a n 的 一半,所以它是等于二分之一 a n。 好, 那这时候我们可以设个圆,把 o d 呢设成 x, 把 o a 呢也设成这个 x, 那么我这时候我再过 o, 那 向这再做一条垂线,在这再做一条垂线,把垂足呢标为点 h。 很 显然,此时我是不是形成了一个直角三角形 o d o h。 现在的话, o d 在 这里面是不是作为它的这个斜边,而 o h 呢,是作为它的这个什么边,这个直角边,显然这个 o d 的 话,它一定是大于这个 o h 的。 那什么时候能等于 o h? 就是 当这个地点和这个 o 点,就是这个 h 点和这个地点刚好重合了,那此时 它的这个斜边呢,刚好肯定是等于这个 o h 的。 有时候这方有一个取等的过程,有一个取等的这个这个过程。好,那这时候我们就把这个 o d 和 o h 用我刚才射源的这个量给它表示进去啊,所以 x 呢,就大于等于。我们看一下, o h 等于呢,我们射的这条边是 x, 因此这个 o b 这条边呢,它应该等于二倍根号二,再减 x, 而这个地方 o h b 始终是一个等腰直角三角形,所以我的 o h 应该等于这条边,再除以根号二,所以它就大于等于 根号二分之二,再减多少减 x, 然后把这不等式解出来,那就根号二 x 大 于等于二倍根号二,再减 x, 把不等式解一下啊,那就根号二,加一倍的 x 大 于等于二倍,根号 x 应该大于等于二倍根号,除以根号加一分母由里化, 那又变成的是根号乘以这个根号,再怎么样减一啊?减一这括号打不下去了,那应该等于多少?所以的话应该是 x 大 于等于这个四减二倍根号,而我刚才说了这个 o d 呢,它是等于 a n 的 这个一半,因此 a n 的 话就应该大于等于八减四倍根号,所以 d 答案呢,它也是对的啊。所以这题大家重点学习一下 d 的 这个模型的一个处理的方法。
76数学戴老师 01:44查看AI文稿AI文稿
01:44查看AI文稿AI文稿你永远干不过一个从初三就每天练习一道压轴题的孩子,因为他清楚的知道,要想数学四次不低于一百一十分,一定要重视压轴题,就用叠变数学压轴题专项训练。一本书包含了中考所有的压轴题型和解析大招,每种题型先通过经典例题教你解析方法, 规范答题步骤,学会例题以后,再做后面的针对训练加以巩固,难度层层递进,帮孩子直击考题。而且每道题都有详细的答案解析,把解题思路和作弊方法 讲得清清楚楚,让孩子吃透一道题,会一类题,练完这本书,考试遇到新题型都能举一反三,每天花十五分钟攻克一道压轴题,考试遇到得心应手,抓紧给孩子准备起来练一练吧!
26优品家百货 08:46查看AI文稿AI文稿
08:46查看AI文稿AI文稿今天来给大家讲一个初三的期末几何压轴题啊,这是一个关于相似三角形综合的题,我们看题如图所示,点 d 在 直角三角形 a、 b、 c 的 斜边 bc 上连接 a、 d, 然后做 d, a, d, a 垂直于 a、 e, 使得 a、 b, a、 d 比 a, d 等于 a, c 比 a、 e, 然后呢,连接 d, e 交 ac 于点 f, 连接 d, e 交 ac 于点 f 啊,若 ac 等于六,这个是六, a、 b 等于八,这是一个六八十模型啊,对不对?也就三、四五。好,我们把这个这个 b、 c 就 十算出来啊。第一个问和第二个问都比较简单,这里面就不讲了,我们主要是看这个第三个问, 当 b、 d 等于二十,求 a、 f 除以 c、 f 的 值等于多少,就是 a、 f 比 c、 f 的 值等于多少。这种题你看 a、 f 和 c、 f 它俩是不是在一条直线上,对不对?像这种在一条直线上,我们要想到什么做平行, 通过平行把它这个笔给转化过去,那这里怎么做平行呢?还有一种,我们还有一种思路是什么呢?我们通过求它的长度,因为这个 ac 是 已知的,那我们要么就是把 af 求出来,要么就是把 cf 求出来,这也可以啊, 这里面我们就是我用的是那种做平行,然后呢,把这个 c、 f 的 长度求出来。我们第一题是不是可以得出 a、 a、 b 三角形 a、 b、 d 和 a、 c、 e 相似啊?我这 b、 d 等于二,我们整个 b、 c 是 十,那我们这个 c、 d 等于多少? c、 d 是 不是八呀? c、 d 是 八,那么这个 c、 e, 我 们通过这个 a、 b、 d 和 a、 c、 e 相似,我们可以把这个 c、 e 求出来啊,我们这通过第一个直接第一个就行。三角形 a、 b、 d 相似于三角形 a、 c、 e, 那 我们这个 a b a, b 比 a c, 那 a b 比 a c 就 等于 b d 比 c e, 我 们带入进去 a、 d 是 八,八除以六等于二,比上 c e, 我 们就可以求出 c e 就 等于二分之三, 这个 c e 值是二分之三啊。好, c e 等于二分之三,我们怎么求?要么求 af, 要么求 cf, 这个是八,而且这个三角形是什么?是一个三四五的模型,是不是?那我们可以做完做这个垂直啊,做一个垂直下来,通过 f 点做一个垂直下来,我们假设这个是 m 点, 那这个 fm 是 不是应该是垂直于 c e? 为什么垂直呢?我们看啊,我们第一个测出这个角和这个角是相等的, 这是直角,那这个角角 b 和这个角 b、 c a 是 应该是互余的,对不对?它和它相等,那它和它加起来是不是应该是等于九十度啊?所以这就是一个直角, 我做完垂直之后,那这两个是平行的,我们通过平行线分线段成比例,那我们这个 dm 比上 dc 是 不是应该等于 f m 比上 e、 e、 c 啊?而这个三角形,这个角,这是一个三四五模型,角是定值,我们通过三角函数,我们知道这是一个, 那这个是短的直角边,这个就 c m 是 短直角边, f m 是 长直角边,而 cf 呢?就是斜边,那他三四五,我们就可以设它。为什么?三 a 四 a 五 a, 我 们再通过平行线和线段成比例啊?我们就是作 f m 垂直于 bc, 交 bc 于 m, 我 们可以得出。还有是 角 b c、 e 就 等于九十度,所以我们这个 f m 就 平行于 e c, 通过平行我们就可以得出对应的线段成比例啊,那我们就是 看射啊,射 c m 等于三 a, f m 等于四 a, 还有是这个 c f 等于五 a, c f 等于五 a, 好, 我们这个就是 e m 比上 dc 就 等于 f m 有 平行吗? f m 平行于 e c 吗?就 f m 比上 e c, 而这个 c d 等于多少呢?我们这个 c d, dc 就是 这整个 bc 是 十吗?十吗? b d 是 二,那我们这 dc 不 就是八吗? dm 是 多少呢?这个是三 a, 整个 dc 是 八,那不就是八减三 a 吗?对不对?八减三 a 比上八就等于 f m 是 多少? f m 是 四 a, 四 a 除以二分之三,这里面减一下,我们 a 是 等于 七十三分之二十四啊, a 是 七十三分之二十四,那我们这个 f f c c f 是 不是应该他是五 a 吗?所以我们这个 c f 就 等于五 a 就 等于七十三分之一百二, c f 出来了,这个 ac 长度是六,那我们这个 af 长度不就出来了吗?对不对? af 长度出来之后就是等于六,减掉七十三分之一百二,这就是 七十三分之四百三十八,减一百二等于三百一十八。 af 长度出来了, cf 长度,那 af 比 cf 长度是不是出来了?所以我们看 af 比上 cf 就 等于 七十三分之三百一十八,除以七十三分之一百二,那就等于一百二十分之三百一十八,这里面不要忘了约分啊,这里面能约多少呢?约掉一个六, 这一百二除以六不等于二十吗?三百一十八除以六五六三十三,六十八应该等于五十三,所以它这个 a f 比上 c f 的 比值就是二十分之五十三, 这里面你看就是通过平行做平行,把这个长度求出来,这里面还用什么三角函数? 这个角是定角,这个模型呢,是一个三四五模型,所以我们可以通过平行线分线的成比例把它设出来,然后求它的长度,求完长度之后,另一个 c f 出来了,那 a f 是 不是就出来了,对吧? 那所以我们这个最后比值就出来了,这是一种思路啊,我们是用几何法做的,还有一种思路是什么?我们可以间隙啊,间隙也是有技巧的,我们怎么间隙呢?我们以 c 点为圆点, 这个是 x 轴,然后这是 y 轴,我们可以建立坐标系啊,假设 c 点就它就是圆点了。 o, 那 我们这个 a、 b、 c, 还有这个 d, 还有哎,这个 e, 它的坐标是不是都能求出来?而且我们这个就是 a c 的 表达式也能求出来, d e 的 表达式也能求出来,对不对?我们这个一样的,把这个通过这个,把这个 c e 等于二分之三求出来,那我们这个 d e 的 表达式和 d e 和 a c, 它的焦点 f 是 能求出来的,这里面我们不用把它 的完整坐标求出来,我们只需要通过横坐标。为什么我们就要通过横坐标写呢?我们 a 点的横坐标是很好求的啊, 这个可以用通过等级法来求啊,这两个相乘面积,然后我们这个是不是也可以用三角函数来求 a 点坐标求出来之后呢?我们这个 f 点的横坐标,我们只要只需要 a 点和 f 点的横坐标之比 就可以了,或者我们就是把这个 a 点到这个,比如说 m 吗?这个是 n, 它的 a f 和 c f 的 比值是不是等于 m m 比上 m c 啊?所以我们只要把它横坐标求出来就算出算出它的比值就 ok 了啊。这间隙法也是一种很好用的,只要用一次函数求它的焦点坐标就行了。 好,今天就讲到这了,如果大家还有什么其他有趣的题,或者还有其他难题的话,可以私信我,或者在评论区留言,我们一起讨论一下。
30嗨,大玉儿 19:44查看AI文稿AI文稿
19:44查看AI文稿AI文稿好,我们来看一下这个二十五题啊,呃,这个二十五题呢,一上来我们观察到呢,它的这个三个系数啊, abc 啊,都是不知道的,对吧?所以呢,这就意味着在接下来的解题过程当中呢,我们需要找三个条件,把它三个 abc 的 系数给它求出来,对吧? 我们来看啊,呃,这句话相当于呢,是告诉我们什么呢?哎,它是告诉我们这个起名字对吧?有与 x, 有 a b 俩点,对吧?哎,左边那个叫 a, 右边那个叫 b, 对 吧?哎,你只要把这个记清楚,别忘了就行啊, 然后注意啊,呃,与 y 轴与 c 的 那个交点呢?哎,哎, y 轴的交点呢?名字叫 c, 然后呢?哎,它这里边呢,这个 顶点 d 的 横纵坐标具备这样的一种关系啊,就是说呢,它的这个横纵坐标的比值是这个,呃,负的三比四,对吧?是这样的一种关系,这个也叫做一个什么呀?数值条件对吧?哎,可以转化为一个什么呢?方程,对吧?好,下面我们再看, 他说呢,直线 b, c 上有两点 e 和 f 点 e 的 坐标是这样,点 f 的 坐标呢?是这样,哎,三角形 d、 e、 f 的 面积呢?即为这个 s。 好, 咱们先不管这个三角形的面积,我们先来看这个第一问,那么第一问呢,我们看啊, 呃,这个 a 等于一, m 等于一,对吧?哎,这就好了,这就相当于告诉我们什么呢三个条件啊,其中第一个条件呢,就是这个二次项系数 a 呀,等于呢? 一,对吧,二次项系数 a 等于一啊。第二个条件呢,就是他过哪个点呢?过一个叫做三斗负四的点,对吧?因为 m 等于一吗?对不对?哎, 第三个条件就是这个点还是抛物线的什么呢?顶点,对吧?哎,这样的话三个独立的逻辑条件就有了,那我们把它综合一下的话,应该怎么办呢?哎, 最好的方法应该是直接用什么呢?直接用这个顶点式,对吧?哎,因为他都这样说了,所以我们就把顶点式给他写成 y 等于 x 减三括号的平方啊,减去四就可以了,对吧?因为 m 等于一啊,这样的话就表示的顶点是这个,对不对? a 呢也等于一。好,下面我们给它展开成一个一般式 x 平方减六, x 加几呢?加五,好在因式分解给它变成一个什么呢?哎,焦点式啊,表示与 x 轴的焦点。好,这就看出来了,对吧?那么他问与他问 a 点的坐标就是什么呢?一豆零,对吧?啊? b 的 坐标呢?当然就是五豆零啊,这个 c 的 坐标呢就是零豆五, 对吧?哎,这样的话呢,几个关键的点坐标就都有了,哎, d 的 坐标三斗复四也有了,对吧?所以呢,我们把这个,呃它的函数图像呢,给它简单的给它画一下啊,给它简单的画一下,哎,呃,我用这个坐标轴的形式啊,我给它画一下吧, 哎,对吧?哎,然后在这里边呢,我们来看它是这样的啊, 我呢把这个地方啊,这个是,呃,原点 o 啊,这个是一一二三四 五,对吧?所以这个呢是那 a 啊,哎,这个是那 b 啊,然后呢往上走啊,这个一二三四五,哎,这就是那 c, 对 吧?哎,这样,然后这个地方呢是那对称轴也是 x 等于三,对吧?哎, 往下边画呢四个点,这就是那个顶点 d, 对 吧?哎,这就齐活了,哎,我们把它给这样画出来, 这个抛物线的图像呢,大致就是这个样子,对吧?哎,然后要注意呢,在这里边还有一个谁呢?哎,还有一个,这个直线 bc, 对 吧?哎,还有一个直线 bc 啊,啊,直线 bc 呢?我们也给他画一下,哎,是哪样?这样, 对吧?哎,右过 b 点,右过 c 点,然后呢,它上面的这个,呃,点 e 和点 f, 我 们先把它画出来啊,哎,点 e 啊, 点 f, 对 吧?哎,然后他说呢,这个点 e 的 坐标是什么呀?哎,点 e 的 坐标是 n 豆 y e, 那 就是这个 y e 啊,不知道,对吧?哎,这个 y f 呢?哎,实际上呢,也不知道,对吧?实际上也不知道,然后他说,此时此刻这个 这个,呃, n 等于二分之五,然后呢,这个 m 等于一,对不对?我们先不管这个 n 等于几啊,我们先不管这 m 等 n 等于几,我们现在是知道 m 等于一,对不对,哎,那么这样的话呢, 这个 bc 的 解析式我们给它干什么呀?可以给它求出来,对吧?哎,那么因为刚才我们已经求出来了这个点 b 的 坐标和点 c 的 坐标了,一个是五逗零,一个是零逗五, 对不对?所以这样的话呢, b c 的 解析式很容易能给它表示出来啊。 b c 的 解析式是 y 等于负 x 加上五,对吧?哎, y 等于负 x 加五,对吧?所以这样的话呢,这个点 e 的 坐标我们就可以知道了,哎,点 e 的 坐标 它实际上是什么呢?哎, n 到负 n 加上五,对吧?哎, 那点 f 的 坐标是什么东西呢?哎,点 f 的 坐标,哎,也可以知道,因为 m 等于一,对吧?哎,这是 n 加一,哎, 逗,然后什么呢?哎,负 n 加四啊,也就是说你算一下就可以知道了,对吧?因为把它们两个的横坐标干什么?哎,都带到哪里边去,哎,都带到这个 b、 c 的 解析式上,对吧?哎,于是呢,就知道了点 e 和点 f 之间的这个坐标了,对吧?哎, 而且呢,我们还能够看出来点 e 和点 f 之间的关系,对吧?哎,然后接下来呢?哎,我换一个颜色啊,它不说,提到了这个三角形 d, e、 f, 对 吧?哎,我把这个三角形 d, e、 f, 哎,给它画出来, 显然这个需要利用什么呢?哎,利用这个我们已经熟练的一个技巧,对吧?哎,就是这个水平宽,铅垂高,对吧?我们呢,把它这个对称轴啊,与这个直线 b、 c 的 这个焦点,我们给它起一个名字啊,起个名字叫什么呢? a, b, c, d, e、 f 都用完了,我们这个焦点叫做 g 啊,叫做 g 啊, 那么这个点 g 呢,相当于横坐标呢,跟点 d 一 样,应该也是三,对,不对,应该也是三,那么这样的话,这个点 g 的 坐标呢?哎,横坐标是三,那纵坐标也带到这里边去,对吧?那就负三加五等于什么呢?等于正二,对吧?等于正二, 所以我们就可以知道,哎, g、 d 这段的长,哎, g、 d 这段的长,就是什么呀?哎,就是点 g 的 纵坐标二和点 d 的 纵坐标负四之间的差,那是几呢?哎,那应该是六,对吧?那应该是六,对吧?哎,那好,那我们再看啊,这个点 e 和点 f 之间差了多少呢?注意, 点 e 和点 f 之间的什么呀?水平距离啊,水平距离差了多少?我们一看点 e 和点 f 之间的水平距离差了几?差了是一对吧差了是一对吧。注意这个地方啊,我在这个图里画的是什么?点 e 和点 f 在 这个对称轴的两侧,那么点 e 和点 f 可不可以去呃,这个,呃,对称轴的同一侧呢?哎,实际上也是可以的,对吧?也是可以的,但是要注意他们俩的横坐腰之间这个水平差距始终要是什么呀,哎,始终是一啊。当然,我这个图里注意啊,我给大家把这个地方给夸张了,给夸大了啊,为了大家看的更清楚啊, 为了让大家看的更清楚,我这个点 e 和点 f 之间的水平距离实际不是一,是远远大于一的啊,这是为了让大家看的更清楚一点,对吧?那么我们可以想象,水平距离不变,这个 g d 的 长度又不变,那么这个 s 当然也是一个什么呀?定值,对吧?它是二分之一 乘以几呢?哎,二分之一乘以六再乘以一,最后等于几,哎,最后等于三啊,最后等于三啊。也就说,其实你不用关心那谁啊,不用关心那二分之五,对吧?哎,不用关心那二分之五啊, 哎,但是你说你用二分之五求出来,最后也是三,对吧?也是三啊,好,这个是这个第一大问的圈一和圈二啊。好,下面我们再来看这个第二大问啊, 这个第二大问里边啊,注意啊。呃,一定要看清楚。这里边怎么样啊,这里边就没了啊,这个地方就没有了啊,就是这个 a 等于一啊。什么?这个 m 等于一,这个就没了啊?变成什么了?变成这个,但是这个条件啊,还是 有的啊,这个条件还是有的,对吧?哎,所以呢,哎,我们要知道啊,所以我们要知道啊,在这个里头啊,在这个里头啊, 结合这个条件啊,和这个条件啊,还有什么呢?还有这个,哎, s 等于六的这个条件啊,结合这三个条件啊,结合这三个条件,好,那我们来看看,那么这个应该怎么处理呢?我们首先先来这样处理啊,因为啊,这个点 d 的 坐标是这个,对吧?我们给他写出来啊,我们给他写出来点 d 的 坐标, 三 m 负四 m, 对 吧?哎,然后呢,哎,点 d 的 坐标呢?是三 m, 呃,喊这个点 b 的 坐标啊, 五 m 都是零,对吧?哎,那么我们看啊,这个点 d 的 坐标相当于是什么呢?相当于是这个,呃,对称轴,对吧?三 m, 那 么于是我们就能够知道点 a 的 坐标一定是什么呀? m 都是零, 对吧?因为什么呢?因为这个三 m 必须得是点 a 的 横坐标和点 b 的 横坐标的一个什么呀?平均数,对吧?所以那么这样的话呢,这个有五 m 和这三 m, 我 们可以求出来点 a 的 横坐标,对吧?哎, 那么于是呢,这样的话呢,这个抛物线的解析是,一定是 a 乘以 x 减去 m, 然后这是 x 减去五 m, 对 吧?哎,我们会看到它长得跟前面那个,呃,前面那一问的里边的有点类似,对吧?只不过是带 m 的 前面那一问里边 m 等于一啊,对吧?哎, 然后呢,我们再把这个什么呢?哎,我们再把这个三 m 逗负四 m 带到这个解析式里边来啊,负四 m 等于 a 乘以,注意,这是三 m 减去 五 m 啊,哎,那么这是负四 m, 对 不对?这是 a 乘以什么呢?二 m, 这个乘以什么呢?哎, 负二 m, 对 吧?哎,那最后得到什么呢? a 等于 m 分 之一啊, a 等于 m 分 之一啊,哎,也就是说呢,哎,这个抛物线的解析师,最终啊,最终它要被表示,为什么东西呢?它是长得这样的啊,它是长这样的啊。 最后啊,它这个 y 等于啊, m 分 之一乘以 x 减去 m 啊, x 减去五 m 啊,这个是他的这个啊,焦点式啊,这个是他的这个焦点式啊。那如果你给他画成一个一般式的话呢?当然也可以,他是 m 分 之一啊, x 的 平方减去六 x, 呃,然后加上 五 m 啊,这个是把它变成这个一般式啊,这是把它变成一个一般式啊,当然你要愿意的话,你给它变成一个顶点式,那是是也可以,对吧?哎,它不就是这个 m 分 之一乘以 x 减去三 m, 括号平方减 四 m, 对 吧?哎,这个是它的顶点,对吧?这是顶点,好,那么这样的话呢,这个抛物线的解析式就表示完了,对不对?那现在他说呢,这个 s 等于几?哎,他说这个 s 等于六,对吧?它 s 等于六,那么这个计算面积的方法实际上刚才怎么样是一样的,为什么呢? 因为这里边点 a 在 点 b 的 左边,对不对?那也就是说点 a 的 横坐标必须得小于谁啊?点 b 的 横坐标,对吧?这就意味着 m 肯定是个正数,是大于零的, 所以呢,他这个图形画出来之后呢,跟刚才长的一定是差不多的啊,特别是这个 m 分 之一,他是 a, 那 也是大于零的,跟刚才长的是,哎,大差不差,对不对?哎,所以呢, 这个到此为止,你都不需要再画一个图了,对吧?那么此时呢,这个 s 跟刚才一样啊,二分之一,注意,就 那个那个数值的那个长度,就是刚才我们看到的那个这个 d g 的 长度就不是什么呀,哎,他就不是谁了,哎,就不是这个六就不是六了,而是六 m, 对 吧?哎,而是六 m, 为什么呢?因为此时啊,这个 bc 啊,此时这个 bc 的 解析式, y 等于负 x 加上五 m, 对 吧?哎,负 x 加上五 m, 对 不对?哎,所以这样的话呢,点 g 的 坐标呢?就是这个三 m, 哎,这个二 m, 对 吧?哎,然后你这样话,跟这个点 d 一 核,对哦,他们俩之间差多少?差了六个 m, 而且 m 是 什么? m 是 一正数,对吧? m 是 一正数, 那么点 e 和点 f 的 横坐标之间差多少呢?你一看就知道,横坐标不就差的那个 m 吗?对不对?所以此时是六,二分之一乘以六 m 再乘以 m, 对 吧?只不过刚才那 m 等于一,对吧?哎,这个时候他说等于几呢?他说等于六,那最后 m 等于几呢? m 等于根号二,对吧?哎, m 等于根号二,是这样的啊,是这样的啊, 对吧?哎,这是这一问啊,这是这一问啊,那也就是说呢,这个 m 的 值呢?是这个根号二啊, m 的 值是这个根号二,那如果要想写出它的这个解析式来呢?那你就把这个 m 等于根号二 c 进去就行了,对吧?哎,最后 c 里边之后是什么呢?是 y 等于二分之根号二, 二分之根号二倍的啊,呃, x 平方减去六 x 啊,加上这个五倍根号二啊,就是把这个 m 等于根号二给他代入就 ok 了,对吧?哎,好,下面呢请你思考一下在这个里头他考察的是什么,对吧?一看线段最小值,线段最小值无非就是那几个模型,对不对 啊,什么将军印马呀,逆等线啊,阿是元呐,呃这个这个胡不归啊,对吧?哎你把这个图在里边画出来就可以了。我给大家呢还是画了一个这个动图啊,这样的话看起来比较方便一些啊,那么大家看 他实际是这样的,对吧?他实际是这样的啊。呃这个,呃需要我们注意的是啊,就是这个 m 他 是可以怎么样? m 是 可以变的啊, m 是 可以变的。哎 那么要注意的是呢这个 n 呢他实际上也可以动,对吧?哎我在这底下把这个辅助线都给大家画完了啊。现在要注意的是他题里说的这个 a f 加 d e 取最小值,那我们来看啊这个 a f 和这个 d e 啊,那我们怎么办呢?我们应该这样办啊。哎我们经过计算我们很容易发现这个 e f 之间的长度是怎么样。哎 e f 之间的长度是 固定的,也就是说在这个 m 确定的情况下啊,在 m 确定的情况下你这个 e f e f 的 长度是不会随着 n 的 变化而变化的啊,不会随着 n 的 变化而变化的。为什么呢?因为我们刚才看完了这个,呃 点 e 和点 f 之间差了一个什么呀?差离 m 对 不对?这横坐标之间差离 m, 然后纵坐标之间的纵坐标之间的差也是那 m 一样的,对不对?哎所以他的这个这个方向上的这个差差距这个长度也是固定的,那这样的话就干什么呢?就好办了,对吧?哎,那这样的话就好办了,对吧?哎,那我们在这里头干什么呢?我把点 a 啊也给处理一下,我们看点 a 的 坐标是什么?他不是这个 m 豆零吗?对不对?哎,点的坐标是 m 豆零,对吧?哎, 点 a 的 坐标如果是 m 逗零的话,我取一个叫什么呀?零逗 m 的 点 a 撇点啊? a 撇点,因为这个方向一定是什么呀?四十五度,因为直线 bc 的是 y 等于负 x 加上五 m, 对 不对?哎,负 x 加上五 m, 对 吧?哎,这五倍的 m 啊, 那么这样的话呢,我们就可以知道什么呢?哎,这条线和这条线一定是平行且怎么样且相等的,对吧?于是这个 af 就 被替换成谁了呢?替换成我这个图里边的 a 撇 e 了,对吧?替换成我这个图里边 a 撇 e, 然后我再做什么呢?我再做这个 a 撇点。关于 bc 这条直线的对称点啊,那这个我为什么做这个对称点?那很很简单的,将军印麻吗?对不对?这个这就比较简单了,对吧?相当于我在这这个地方干什么呢?我构成了一个 a 撇 a, f, e 这样的一个什么呢?平行四边形,对吧?哎,构成了一个平行四边形啊,那么这个平行四边形这不上下来回动吗?对吧?哎, 在动的过程当中,最终 af 这条线通过 a 撇 e 的 中间代换,被变成了 a 两撇 e, 对 吧? a 两撇 e, 那 你说蓝的和红的什么时候这个和它是最短的呢?当然是给它拽直了的时候, 哎,它就是这个哎,最短的了,对吧?哎,那么现在呢,我们就是干什么呢?我们把这个 a 两撇的这个什么呀?哎,这个坐标给它求出来 a 两撇的坐标实际上非常容易能够求出来, 对吧?因为 a 撇点的坐标是什么呀?是这个,呃,零豆 m, 对 吧?哎,那么这个点到这个点的距离就是几个 m, 那 当然是四个 m 了,对不对?那你想啊,你往这一画这个垂线, 这个不还是等腰直吗?对吧?你要往这把它画齐了的话,这这地方,这不正方形啊,对吧?所以这条线的长度一定是多少?也是四 m, 对 不对?对吧?而且他跟 x 是 平行的,你往下画这条线长度是五 m, 对不对?没错吧?哎,所以啊,这个 a 两撇,它的坐标是四 m, 都是什么呀?哎, 四 m 都是五 m 嘛,对吧?哎,是四 m 都是五 m, 而点 d 的 坐标是什么东西?三 m 都是负四 m, 对 不对?哎,所以这样的话,哎,他们的这个所谓的这个,这个这个最小长度,那最短长度,比如说我让他是这个,呃,长度是这个 d 啊,这个这个 minimum 最小值,哎,那就是什么呢?就是根号下看横坐标差了多少?横坐标差了 m, 对 吧?哎,纵坐标差了多少?纵坐标差了什么呀?哎,这个九 m, 这走你括号平方,对吧?哎,就算出来了,对吧?这个东西等于什么呢?等于,哎,这个我写下头吧, 哎,这个东西它最后等于什么呢?哎,等于八十二 m 的 平方,对吧?哎,根号加啊,根号加八十二 m 的 平方,对吧?哎,而此时此刻啊,而此时此刻,我们刚才求出来了啊, 此时这一问里 m 等于几呢? m, 这不等于根号二吗?哎,你给他带进去,对吧?哎,你给他带进去,对吧?于是呢,这个东西就等于什么呢?哎,它就等于,哎,这个,哎,我这个橡皮没弄好啊,哎,这样啊, 走,哎,那么在这里头,根号下八十二乘以二,对不对?叫二倍根号四十一,对吧?二倍根号四十一,对不对?哎,那么这个就是什么呀?哎,就是题目里头要让我们求的这个,呃,这个最小值,啊,最小值。 然后呢?接下来让我们写出什么呢?点 e 的 坐标,对吧?点 e 的 坐标,那么这个时候这个点 e 的 坐标,那就比较容易能求出来,对吧?啊,因为什么呢?这个点 a 的 坐标,这不确定完了吗?点 a 的 坐标是这个四倍根号二,逗,呃,五倍根号二,对吧?哎,然后呢,这个点 d 的 坐标是三倍根号二,逗,负四倍 根号二,对吧?哎,那于是呢,哎,这条直线的解析式,我们就能够给它确定出来,对吧?哎,你待定系数法,很容易能给它确定出来,而 y 等于,呃,这个九 x 减三十一倍根号二,对不对? 和谁连力呢?和 bc 这个连力, bc 的 解析式是什么东西? y 等于负 x 加上五倍根号二,对吧?哎,你这两个式的连力就求出谁来呢?求出点 e 的 坐标来了啊, 最后这个点一的坐标是什么东西呢?哎,五分之十八倍根号二,豆,啊,五分之七倍根号二,哎,这个是点一的坐标啊,这个是点一的坐标,哎,听懂了吗?
49天津数学王天元 01:35
01:35 00:23查看AI文稿AI文稿
00:23查看AI文稿AI文稿中考数学五类几何最值压轴题,全部吃透,稳进班级前三!中考数学五类几何最值压轴题,将军印码最值问题 动点辅助圆类最值!四点共圆瓜豆原理类最值!
39白露学习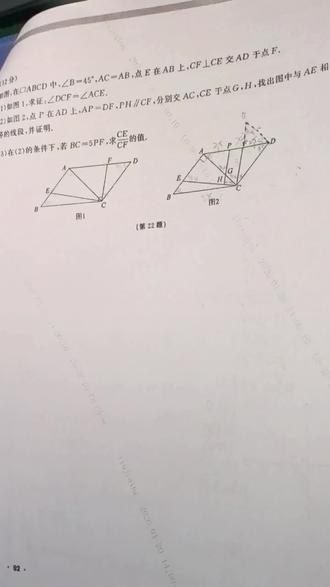 04:08查看AI文稿AI文稿
04:08查看AI文稿AI文稿今天我们来看一道中考模拟卷的压轴题,那么这道题是运用了全等和相似的知识。我们先读一下题。在平行四边形 a、 b、 c、 d 中,角 b 等于四十五度, ac 等于 ab, c、 f 垂直 c、 e 那 么我们第一问,要求证角 d、 c、 f 等于角 a、 c、 e, 那么因为这是一个平行四边形,所以 ab 是 平行 c、 d 的 角 b、 c、 d 是 一百三十五度,那么这个角是九十度,所以说角 ecb 加上角 fcd 就是 四十五度。 那么因为 ab 等于 ac, 那 么角 a、 c、 b 也是四十五度,所以角 e、 c、 b 加上角 a、 c、 e 也是四十五度。那么我们就能证出角 d, c、 f 等于角 a、 c、 e 那 么我们再看第二问 p 在 a、 d 上, a, p 等于 d f, p h 平行 c、 f 然后我们要找出与 a、 e 相等的线段并证明。这时我们可以先进行一个倒角。 那么因为第一问,我们证出角 a、 c、 e 等于角 d、 c、 f, 那 么我们就设它为而法,那么这个角就是九十减而法。因为平行,所以角 p g, a 也是九十减而法。 那么这时又因为 a、 c 等于 cd, 我 就看到了一边一角,想到了构造在 q、 d, 呃,在这个三角形里面做 q、 d 垂直 cd, 那么因为角三角形 a、 c、 e 和三角形 q、 c、 d 中,呃,已经有一个等角和一个等边,我们又做了一个垂直,所以说这两个三角形就全等了。 a、 e 就 等于 d q, 那么因为角 q、 d、 c 是 九十度,角 a, d, c 是 四十五度,所以角 q、 d, a 也是四十五度。那么这时又有一组等边, 通过我们之前的倒角又能得出角 a、 j、 p 等于角 c、 q、 d 所以 在三角形 a p j 和三角形 q f、 d 中,呃有一组边相等,两个角相等,那么它们就全等了。 q d 就 等于 a h 等于 a e, 那 么我们就能证出 a e 等于 a h。 第三问,在二的条件下, b c 等于五倍的 p f, 我 们要求 c e 比上 c f 的 值, 那么我们可以设 p f e x, 那 么 bc 就是 五 x, ad 就是 五 x, 因为 ap 等于 f d, 所以 它们就是二 x。 那 么这时因为第二问,我们证出 c e 等于 c q, c e 比上 c f 的 值就转化为 c q 比上 c f 的 值。 这时我们发现三角形 q、 f、 d 和三角形 a、 f、 c 是 相似的,因为 d、 q 是 平行 ac 的, 那么我们就能证出 a、 f 比上 f d, 也就是它们的相似。比是三比二, 那么 c f 比上 f q 就是 三比二, c f 占三分, f q 占两分,那么如果要求 c q 比上 c f 就是 五比三,那么第三分的答案就是五比三。
30处女宝宝 08:22查看AI文稿AI文稿
08:22查看AI文稿AI文稿好,各位小伙伴,大家好啊,呃,今天给大家分享的这个题目呢,是关于二倍角的一个题啊,这个题呢,拿拿了我好长时间,今天呢,终于把它做出来了,一并分享给大家 好了,说入图啊,在 r t 三角形 a、 b、 c 中,角 a, c, b 是 直角。好了,这个垂直的直角三角形对吧?点 d 在 b c 边上,并且告诉你了, b、 d 等于五 啊, c, e 又垂直于 a d, 然后 c、 e 等于六。 另外我们还知道角 c, a、 d 等于角二倍的角 b 啊, c, a、 d 在 这个位置,它要等于角 b 的 二倍。好了,为了方便体现的话呢,角 b 的 话,我给它设成阿尔法,那么角 c、 a、 d 就 等于二阿尔法,对吧? 当然了,我们这个图里边呢,还有,你看看角啊,我们还有一个角是谁呢?这个角阿尔法哎,他加上这个角九十度,对吧?而这个点呢,加上这个角呢,他也是九十度, 所以这个角呢,也是阿尔法啊,也就是这图中啊,实际上现有的是两个阿尔法角了,但是这个阿尔法阿尔法呢,和这个阿尔法只是一个倍数关系,那么我们接着我们就很好的处理,我们再构造一个阿尔法,我们看看怎么构造啊, 怎么把这个单倍角构造成二阿尔法。好了,我们可以这样考虑啊, 单倍角,一个角阿尔法勾搭成两倍的阿尔法,我们通常采用的方法呢是翻折,好了,我把这个三角形 a、 c、 b 沿 ab 翻折,翻折到 a 这个 b、 f 的 位置,那么这个角呢,也会是阿尔法,对吧?呃,那么这个整个这个大角呢,他就是阿尔法了。好了,途中呢,你看看阿尔法就有 阿尔法,我怎么构造阿尔法,这个技巧我就出来了,但是我发现呢,这个时候啊,虽然构造出 a、 c、 b 和 abf 是 全等的,但是还是没法解决问题啊, 结果我们发现啊,这个角 f 这个位置是直角对吧?角 a、 c、 b 也是个直角,那么 a f b c 一个四边形,这个四边形呢,其实是四点共圆 啊,四点共圆好了,呃,关于这个问题,我们四边形的问题的话,再考虑到转化为三角形来做,所以我们把 f a 和 bc 再延长,相交于点 g, 那么我们大家就知道了,来看看这个 f、 b、 g, 它是二阿尔法,根据我们说 a f、 b c 这四点是共圆的啊,对角互补,所以这个角我们判断出它会等于角 f b g 也会等于二阿尔法 也等于阿尔法啊,那这样的话,我们大家来看啊,来看。首先我们看到的是什么呢? 我们会看到第一个,当我演完演唱完之后,我会发现这个 a c g 和 a c d 三角形, a c g, 它是全等于,呃,三角形叫做 a c d 的 对吧?因为两个都是由 r 二 r 二 r 二角,然后有垂直关系,这个 a c 是 公共边,肯定是垂直的,那么这样的话我就知道了,这个 c g 呢,实际上是等于 c d 的 啊, cd 等于 cd 好 了,为了方便起见的话呢,我们干脆我们设它,这两个怎么样都等于 x 啊,都等于 x, 那 么这样的话一看,哎呦, 呃,因为第一次我们是复制过来的,那么 c b 和 b f 应该是相等的, c b 的 话,它会是 x 加五,对吧? f b 呢,也应该是 x 加五啊,这是我们发现的第一个,呃, 全等的一个,我的这个用法,对吧?来,我们接着看,图中有这么多的二 r 发夹,我会考虑我用 这个相似关系啊。第一个相似关系,我们看看我们这个元素,一只元素集中在哪个三角形里边了,对不对?好,以二阿尔法为边的三角形,我给他标出来啊,二阿尔法 不是为角的,那么第一个是就是三角形 c, 呃, e、 d, 对 吧?这个三角形一定是相似于谁的呢?我看看 c、 e、 d 一个内角是二阿尔法,那么它肯定会相似于谁啊? 是 b f g 三角形 b f g。 哎,这个三角形都是有一个锐角,是二阿尔法的,这个 直角三角形,对吧?好了,我们先验着这个路来做啊,因为这个里边的条件最多的,对吧?所以那我就看看清楚了,这个 c e, 它应该比上 b f, 呃,等于 cd, 比上 b j, 对 吧?也就变成了 六比上 b f 是 x 加五,等于 cd 是 x, 比上 b g, b g 是 二, x 加五,这个时候我们可以算出 x 两个值, x 等于十, 或者 x 等于负三,这个呢,要舍去啊。好了,我们现在看看,当我们算出这个值之后啊, 我们来看,那么这个 x 就 等于十了,对吧?这是十的位置,这是直角。好了,我们要求 a、 d, 那 很明显我们要用的是什么呢? a c、 d 又是个直角三角形做的斜边上的高,所以我们肯定是用的是三角形,叫 a c、 d, 应该相似于三角形 c e、 d 啊,如果你非常熟练的话,你可以这个地方可以直接使用这个,呃,适应定律,对吧?这个 c 地方 它会等于什么呢?等于 e d 乘以 ad。 好 了,我们看一下 c d 是 十, c e 是 六,那么 e d 呢?这个长度呢?应该等于八, 对吧?所以就变成了什么了呢?呃,十的平方等于八乘以 ad, 所以这个 a d 应该等于二分之二十五。好了,这样的话,我们就通过将这个 一倍角 get, 通过翻折来变成二倍角,最终让这个问题呢得到了解答。当然了,这个题目里边还涉及到很多的相似关系,这个都需要大家去掌握的。 ok, 你 听明白了吗?
76老冯讲数学 02:45查看AI文稿AI文稿
02:45查看AI文稿AI文稿一分钟学会一道几何压肉题!在抛物线上找到点 q, 使得 q a b 这个三角形的面积呢,和这个黄色的三角形面积是相等的。那 q 点的位置呢?一共有三种情况,其中第一种啊,非常的好找,只需要过点 p 做 a b 的 平行线,那这条平行线和抛物线有个交点 q 连接 a q b, q 所形成的这个三角形,就和这个黄色的三角形面积是相等的。为什么这两个三角形有共同的底边 a b, 那 因为平行线间的距离啊,出入相等,所以过点 q 向 ab 做垂线段和过点 p 向 ab 做垂线段,这两条垂线段的长度啊,是相等的,那这两个三角形 同底等高,那么它的面积啊,就是相等的。点 q 的 坐标怎么求呢?因为蓝线和这条直线是平行的,所以它们有相同的 k 值,这条直线的 k 值啊, 是负一,我们可以从它的解析式中看出来,所以呢,可以设这条蓝色的直线,它的解析式为 y 等于负 x 加 b。 那 又因为点 p 也在这条直线上,所以我们把 x 等于一, y 等于四,代入就可以求出 b 的 值等于五。那因为点 q 是 蓝线和抛物线的交点,所以呢,我们连立直线和抛物线的 方程,就可以得到一个方程组,点,这个方程组呢,就可以得到点 q 的 坐标是 x 为二, y 呢为三,这只是其中一个满足条件的点。还有两个,这条蓝色直线的解析式是, y 等于负 x 加五。直线 ab 的 解析式是 y 等于负 x 加三。哎,这里是加三,这里是加五,那就说明这条蓝色的线是直线 ab 向上平移了两个单位长度 得到的,那如果我们把直线 ab 向下平移两个单位长度,那所得到的这条红色的直线,它的解析式应该是 y 等于负 x 加一, 那么它也和这个抛物线有两个交点,这两条平行线间的距离和这两条平行线间的距离应该是相等的吧。所以我们把点 q 和点 a、 点 b 连接起来,所形成的这个 三角形的面积和这个三角形的面积应该是相等的,因为它们是同底等高的,那这个焦点 q 呢?也是一样的道理。 那我们只需要把这条直线的解析式和抛物线的解析式连立成一个方成组,解这个方成组呢,就可以得到这两个 q 点的位置啊。这样呢,我们就找到了三个满足条件的点。
73潘小童讲数学 10:08
10:08 15:13查看AI文稿AI文稿
15:13查看AI文稿AI文稿哈喽,同学们,大家好,我是大习老师,今天呢,我们来一起啃一道硬骨头。二次函数图像翻折后与相似三角形存在性的综合大题啊,这类题呢,经常的出现在中考的压轴的位置, 因为什么呀?它融合了函数图像变换方程以及几何模型啊,听起来比较复杂,但是只要我们一步一步的拆解就能够完全的掌握。现在请你准备好你的纸和笔,我们一起开始做题吧。好啊, 来第一步呢,永远是审题,我们说审题,我们得先知道它的底牌是什么,对不对?我们是不是可以通过这个抛物线它与 x 轴的交点, 然后呢,咱们令 y 等于零。老师在这写啊,这是第一问,咱们令 y 等于零,就将这个抛物线转化成为一个一元二次方程, 然后呢,我们可以解得一元二次方程,它的解,同学们关于解一元二次方程有什么问题吗?有问题的话可以在评论区。哎,给老师留言啊。好,咱们后续的话,如果同学们都有一些问题的话,咱们就再出一期视频,去专门的讲一下如何去解一元二次方程,好不好?嗯,这个呢,现在你可以暂停一下视频,自己解一下,对不对?好啊, ok, 暂停一下。嗯,好,想必你已经解出来了。咱们说这个 x 一 等于多少呀?等于负一, x 二等于二,对不对? 所以说什么呀,那这一块肯定是负一,这块是二喽,那 a 点的坐标是不是就是负一零, b 点的坐标就是二零了,对不对?哎,接下来呢,就是关键的操作啊,我们将抛物线在 x 轴下方的部分沿着 x 轴翻折,这意味着什么呢? 我们可以看到图像啊,在 a b 两点之间,也就是 x 此时大于负一小于二的时候,抛物线在 x 轴的下方 翻折后呢,这部分会跑到 x 轴的上方,并且呢,形状像一个倒扣着的碗,对不对?哎,数学上,我们就是把原来这部分对应的什么呀?外值,也就是啊, x 方减 x 减二,对不对?怎么地啊?整体的给它取一个相反数就可以了啊,就从 x 方减 x 减二, 给它取一个相反数就可以了,在它前面加一个符号就可以,对不对?哎,那这部分的图像是不是就变成了 y 等于负的括号, x 方减 x 减二啊,展开负, x 方加 x 加二,对不对?好啊, 所以啊,得到的新的图像,这个 w 是 不是就是一个分段的函数呢?嗯,因此第一问的答案就是,图像 w 位于线段 ab 上方,也 就是 y 大 于零的部分,其函数关系式为 y 等于负, x 方加 x 加二啊,咱们要写一下, x 的 取值范围是 x 大 于负一小于二啊,这是我们所有分析的一个基础啊,请你务必记牢好不好? 好,第一问呢,我们已经做完了,来,我们看一下第二问。第二问呢,他说若直线 y 等于负, x 加 b, 与图像 w 有 三个交点啊,让你结合图像直接的写出 b 的 值 啊,我们可以看一下,很多同学呢,在做这一问的时候呢,他可能会回答出来一个答案啊,也就是说什么呀,这个直线呢,与这个抛物线交点在外轴上是 c 点的时候啊,他知道这个 c 点,咱们说 c 点的纵坐标是不是根据刚才你第一问求出来的啊,什么呀? 那是不等于零二啊,所以说第一种 b 的 情况呢,是 b 等于二,这是很多同学能直接看出来的啊,因为结合图像对不对?结合图像呢,是一个体眼啊,好,大家都能看出来,那大家想一想,还有没有其他情况呢?嗯,这样啊,老师拿一个 牙签给大家去比划一下,好不好,看一下啊,这个牙签呢,代表着这条直线, 对不对?哎,你看啊,咱们说这条直线是 y 等于负 x 加 b, 证明它的斜率是负一,对不对?它的斜率已经确定了啊,但是 b 值咱们不知道,所以说它的图像是不是可以怎么的啊? 哎,一直平行着这条直线去运动,对不对?哎,只要它斜率确定, b 值可以是与 y 轴上的任意的一个交点,对不对?是这样的吧,啊,大家应该能看出来,对不对?好, 那此时呢,咱们说这条直线,它与这个 w 图像在 a b 上方的这一部分相切的时候,老师问你啊,你看好我现在把这牙签去掉啊,老师给你画一个 嗯,这个抛物线,你看,此时这是一个焦点啊,这是相切的点,这是一个点,你说这个时候是不是这个直线还是与 w 有 三个焦点呢?对不对?一二三,对吧?好,那这个时候你怎么求出来 b 的 值呢?嗯,想一想, 此时你知道了这条直线,它的表达式是 y 等于负 x 加 b, 你 还知道它与这部分的图像相切,所以应该怎么地? 连立两个方程,对不对?哎,连立谁呀?连立 y 等于负 x 加 b, 还有 w 图像在 ab 上方的这部分的函数关系式对不对? y 等于负, x 方加 x 加二,对不对?哎,连立完以后,我们说求一条直线与一个抛物线的交点的情况,我们要怎么地啊? 有一个焦点,令单调等于零,对不对啊?好,这个时候呢,我们可以把第一个这个函数 y 等于负 x 加 b, 哎,带到第二个这个函数表达式里面,对不对?它就变成了一个一元二次方程,然后你再令判别式单调等于零,是不是就可以求出来了 b 的 值了呀,对不对?好啊,咱们可以求出来 b 的 值是谁呀? 嗯,好啊,很多同学觉得这边有一点问题,来,咱们一块去做一下啊。来,咱把第一个啊,老师给他写一个,嗯,小一啊,这样吧,这样小一和这样小二,咱们将一带入到二里二中, 好,是不是就变成了负 x 加 b 等于负, x 方加 x 加二啊,对不对?好,来,把它给整理整理,变成了 x 方减二, x 加 b 减二等于零,对不对?此时得判别是得等于 b 方减四, a c 对 不对? b 呢?是这儿呢,对不对? 负二的平方减去四乘以一乘以 c, 是 这一部分啊,不要带错。好,它是不等于零啊?来,你看这个,现在这个表达式里面是不是只有 b 一个未知数啊?能不能求出 b 的 值?到这就不用老师再帮你求了吧。啊, b 是 不是可以求出来啊? b 等于。来,你也可以暂停一下,自己求一下啊。 好,来, b 等于三,对不对?好啊,所以说这道题呢,它是有两个答案的啊, 好,第三问呢,它是相似三角形的一个存在性的问题,对不对?哎,我们要先把已知的条件去衡量了,哎,首先 o 点呢是零零,我们知道 b 点呢是二零, c 呢,是 w 与 y 轴的一个交点,对不对?代入呢? x 等于零呢,可以得到 c 点的坐标呢,是零二啊, 所以说这一点呢,它的坐标标是二,所以说三角形 o b、 c 啊,三角形 o、 b、 c 怎么了呀?它是一个等腰的直角三角形,对不对?哎,它是等腰直角三角形。现在呢,动点 p 呢,是在 x 轴的正半轴上或点 p 做 y 轴的平行线 交直线, b c 于 m 交图像, w 于点 n。 问题是是否存在点 p 呢?是三角形,这两个三角形相似, n c m 和 o b c 相似,对不对? 接下来呢,我们就要讲我们通关的秘籍啊,面对相似存在性的问题的时候,我们的秘籍就是,第一步,首先你要确定固定母三角形的一个形状 啊。第二步是分类讨论子三角形的对应的一个关系啊,母三角形是谁啊?就是现在你确定的已知的啊,没有动点的这种三角形啊,你看 o、 b、 c 是 不是?它就是固定在这呢,对不对?哎,母三角形 o、 b、 c, 它是一个什么三角形?咱们刚才说它是一个等 腰直角三角形,它的三个角是固定的,对不对?九十度,一个直角,还有两个四十五度,对吧?好,那么三角形 ncm 要与它相似的话,那它必须也是一个等腰直角三角形,对不对?哎,到这能理解吗? 嗯,好啊,且它的直角的顶点是不是可能是 n 呢?也可能是 c, 甚至也可能说是 m 中的任何一个,对吧?哎,这个就是我们分类讨论的一个根源啊。好,那首先呢,第一种情况啊, 我们假设这个直角顶点是 n, 嗯,咱们可以画一个啊,比如说,我现在画这条 啊, p 点在这啊,假如 p 点现在在这,你看一下此时这个三角形 c n m 是 不是这样的一个三角形啊,对不对?哎,咱们说,如果你的顶点,现在你的直角顶点就是 n, 你 看老师画这个是不是就很像啊?直角顶点是 n, 那 么角 c n m 是 不是就是九十度呢? 嗯,此时啊,怎么地啊? c n 是 不是等于 m n 呢?因为它是一个等腰直角三角形嘛,对不对? c n 等于 m n, 哎,这是最可能出现多解的情况啊,我们需要利用什么呀? n 在 图像 w 上,以及呢? c n 是 垂直于 m n, 因为什么 m n 是 数值线啊,所以说 c n 必须是平行线,所以说什么呀? n 点的纵坐标和 c 点的纵坐标是不是就相同了?那此时怎么的啊? n 点纵坐标是不是也等于二啊?哎,咱们能得到此时 y n, 哎,就是 n 点的纵坐标是不是也等于二呢? 好,那么我们可以把什么呀? y n 等于二,分别的代入到图像 w 的 两段的一个解析式中,对不对?你看,咱们说 啊,你如果把 c n 给它延长,那这条直线给它延长的话,你想一想它是不是与 w 这个图像,因为 w 图像,你看它是这样的一个图像,对不对?它可能与 a b 上方这部分有个交点,与什么呀?在 b 点的右边这部分图像有一个交点呢,对不对? 哎,它是由两段解析式嘛?是不是咱们把 y 等于二呢?分别地带入到这两段解析式中,好,来,咱们说怎么地啊?在这写啊,当 t 大 于零小于二的时候啊,这个 t 大 于零小于二的时候,是不是咱们就带中间这部分的呀?中间这部分的函数表达是在这呢啊,在这呢, 此时怎么的呀?带进去负 t 方加 t 加二等于二啊,解得来 t 等于暂停一下,可以啊,自己解一下, ok, 好, t 什么呀? t 等于一,对不对?哎,此时呢,这种情况呢? t 等于一啊,这个 t 这个 t 是 不是也就是 n 点的一个横坐标啊?咱们之前设它的横坐标是 t 二嘛,对不对?相应的 p 点的横坐标是不是也是 t 啊? t 零对不对啊?这个要知道啊,那 t 此时 t 等于一,哎, p 点呢,它的坐标呢? 是不是此时就是怎么的?一零啊,是不是?哎,这是第一种情况, p 一 好,那当 t 大 于等于二的时候,老师说,在这部分图像你要求 y 等于二的时候,要带入上面这个函数表达式中,对不对?好,来,带进去 t 方减 t 减二等于零,解得 t 等于多少?可以暂停一下啊,等于二分之一加根号十七,对不对?哎,那此时证明 n 点在这的时候,哎,这是 n 一, 这是 n 二的时候, n 点在这时候,它的横坐标就是二分之一,加根号十七。那此时如果说这样画一条直线的话, 它与 x 轴交点, p 点的横坐标是不是也是二分之一加根号十七呢?所以说 p 二就是二分之一,加根号十七,零啊,好,这是直角顶点在 n 的 时候,那么老师说,如果说直角顶点 在 c 的 时候呢,直角顶点是 c 的 时候,我们说什么呀? n c 是 不是肯定是垂直于 c m, 对 不对?哎,那你说是不是可以这样画呢? 怎么样?咱们把这个函数图像给它往上演一演?哎, 好,你看,此时它与这个抛物线这部分的焦点坐标呢,是 n 点,对不对?哎,然后呢,咱们再做 p, m 是 平行于 y 轴。 好,你看,此时呢,这个点是 p 点啊,这个点是 m 点 p c m 呢?同样是平行于 y 轴交 bc 呢?于点 m 交图像, w 于点 n, 对 不对?哎,你看,现在你可以看这个三角形 ncm 这个三角形对不对?哎,此时呢,咱们说 c 点呢, 它就是一个直角的顶点了,对不对?哎,好,老师说,因为这个 nc 垂直于 c m, c m 是 不是也就是 c b 这条直线呢?对不对? c b 这条直线是 y 等于负 x 加二,对不对?哎, c b 这条直线是 直线, c b 表达式可以是 y 等于负 x 加二,对不对?那老师问,你,与它垂直的 c n 表达式可以表示出来吗? 它们的斜率是相反数,然后呢,与 y 轴的交点是一样的,对不对?所以说它呢,是 y 等于 x 加二,对不对?好,这条直线你也知道了。然后呢,它与 w 的 图像交了点 n, 对 不对?能不能连立这个方程,求出来 n 点的横坐标呢? 好,我们连立方程 y 等于这部分 c n 的 y 等于 x 加二与什么呀?圆这个 w 图像在 b 点右边的这部分是不是?这个还是表达式呀? y 等于 x 方减 x 减二啊,连立你可以得到 x, 嗯,它有两个值啊,可以暂停一下,自己求一下。好,老师说啊,第一个值是 x 一 等于一,加根号五, x 二呢,等于一减根号五,因为咱们说它是在什么呀? x 轴正半轴上一个动点啊,所以说这个是要舍去 好,那 n 点的横坐标是不就知道了呀? n 点跟 p 点的横坐标一样,那此时老师说 p 三是不就求出来了呀?是什么呀?一加根号五零对不对? 好,这个是直角顶点,在啊,相应的在 n 点和 c 点,咱们都知道了。那来,咱们再看一下 m 点,假如说第三种情况,咱们老师在这写了啊,第三种情况就是直角顶点 是 m 的 时候,你说这种时候可以出现吗?嗯,咱们说,如果说你说直角直角顶点是 m 的 话,那老师说 c m 肯定是垂直于 m n 的, 对不对? c m 垂直于 m n 可能吗?因为什么呀? m n 它是一直平行于 y 轴的,对不对? c m 呢?它还是一条斜率是负一的固定的,这个直线对不对?它的学历已经确定了啊,所以说它能垂直于,它俩能互相垂直吗?不可以,对不对?所以说这种情况是不存在的, 对不对?好啊,所以说呢,第三问呢,总共就有三个答案,第一个答案呢,就是二分之一加根号十七零,第三个就是一加根号五零。好,这道题您感觉难不难呢? 好的,这道题做完了之后呢,我们来一起回顾一下啊,攻克这道题的一个核心的方法。首先第一条是翻译条件,我们要将翻折 翻折翻译成为分段的函数,将什么呀?三个焦点翻译成为临界的直线啊。然后呢,包括数形结合啊,结合图形呢,就是让我们要进行数形结合时刻的让图形直观,相互印证啊。 最后呢,就是要进行分类的讨论啊,相似存在性的问题呢,一定要根据可能的直角的顶点或对应的边进行不重不漏的分类啊。好, 如果呢,你觉得这个视频呢,对你有一定的帮助,那么请点赞关注我吧,我们下期再见吧,一起来挑战更多的数学难题好不好?好,我是大习老师,我们下期再见。拜拜。
37数学大琪老师 01:46查看AI文稿AI文稿
01:46查看AI文稿AI文稿今天向大家分享一个初中数学里面流氓解法,间隙法。当我们在做几何压轴题的时候,做题没有思路,不知道如何做辅助线,不知道几何模型的情况下,还想把分数拉下,那么这时候推荐大家用一下间隙法来进行暴力求结。 那么间隙法一般适用于平面出现正方形、矩形、平行四边形或含有对称性的等腰三角形、等边三角形等几何图形时,它需要用到的知识储备 分别是两点间距离公式以及中点坐标公式。那么对于此题,正方形 a、 b、 c、 d 边长为六,四个点分别是四条线段的中点,让我们去求 o、 m 长。此题中大家如果完全没有思路,那么我们可以采取间隙法,以点 b 为坐标原理, 以 b、 c、 a、 b 所在的直线为 x 轴,外中构造平面直角坐标系。那么由于 a、 d 等于六,我们根据图形特征可求出 a、 c、 d 三个点的坐标,那么又因为点 e 是 c、 d 中点,根据中点的坐标公式, 我只需要将 c、 d 横坐标、纵坐标分别相加除以二,可得点 e 坐标为六三。那么同样方法, f 为 a、 e 两个点的横纵坐标相加除以二 为三,二分之九。那么重复刚才的操作,我们可得点 o 坐标为三三点 f 坐标为二分之三,四分之九。 那么接下来要求 om 的 长,我们只需要用到两点间的距离公式,将 o 和 m 的 坐标带入即可。那么此时计算过程给大家省略,可轻松求出此题答案为四分之三倍的编号,搞定收工, so easy!
3701初中数学王老师🧑🏫 00:19查看AI文稿AI文稿
00:19查看AI文稿AI文稿初三数学最难的五大压轴题全部吃透!开学逆袭前三!中考数学五类几何最值压轴题一,将军引马最值问题二,动点辅助圆类的最值三四点共圆类四,刮豆原理类完整版。
22四叶草🍀 04:09查看AI文稿AI文稿
04:09查看AI文稿AI文稿初中数学孩子每天都在刷题,为什么一到考试最后那十几分就是拿不到?因为你练的可能都是假压轴题, 想真的突破,你就得用这个蝶变初中数学压轴题专项训练十月新版!今年中考的压轴题型全在这里了!看他的方法特别狠,先叫大招,每种题型 先用一道经典例题,把步骤掰碎了讲给你听,再猛刷题。跟着就是专门针对的训练,难度层层加码,直击考点,答案超详细,重点在这,每道题都不只是给个答案, 而是把怎么想的全讲明白,让孩子吃透这一道,就会这一类。很多孩子题海战术,浪费时间用这本书,每天就花十五分钟 死磕一道真正的压轴题,坚持一个月,你会发现孩子在看到压轴题眼神都不一样了,不再是害怕,而是知道从哪下手。初中数学的差距就是这么拉开的,别让孩子在压轴题上永远丢分!每天十五分钟,用对方法练对题新版链接就在下面,为孩子抓紧准备起来! 初中数学孩子每天都在刷题,为什么一到考试最后那十几分?
0星恒百货




