中考几何题大全
粉丝9896获赞2362
相关视频
 00:26查看AI文稿AI文稿
00:26查看AI文稿AI文稿二零二五中考十道最难的压轴题,天津,填空压轴。浙江,二次函数与几何综合。福建圆的综合,武汉几何综合。 北京,新定义综合。陕西几何和函数综合,广东函数和几何综合,重庆几何综合,哈尔滨几何综合,长沙,二次函数综合。
45杜老师聊学习 00:42查看AI文稿AI文稿
00:42查看AI文稿AI文稿中考数学一共有二十五道题,答题时间是一百二十分钟,平均算下来每五分钟就要做的一道题,其中几何题更是费时间,如果每道题都要现场想思路破解,考试很难做的完。建议孩子从初一开始学着六十八个初中几何模型,大体有思路,小题套模型, 提高解析效率。它包含初中几何全部解析模型,你看三角形风筝模型、 a 字相似模型、动点将军硬马 在码点旋转,每个模型结论是什么,怎么画辅助线,怎么证明,讲解都很详细,有不懂的你就扫码看视频讲解。掌握了这些解题模型后,就基本摸透出题的规律了,做题就真的像抄答案一样简单,抓紧练习起来吧!
 00:23查看AI文稿AI文稿
00:23查看AI文稿AI文稿中考数学最难的经典几何题,全部吃透,稳进班级前三!中考数学五十道经典几何题, 第一题、第四题、第六题、第十题、十四题,完整版可分享!
42白露学习 00:21查看AI文稿AI文稿
00:21查看AI文稿AI文稿中考数学最难的五大压轴题全部吃透!开学逆袭前三!中考数学五类集合最值压轴题!一、将军引马二、动点辅助圆三四点共圆, 刮到圆里完整版!
21爱分享的苏 03:54查看AI文稿AI文稿
03:54查看AI文稿AI文稿初衷间的各种几何模型有它的适用性,你每学一个模型,你一定要认真的掌握它适合的哪种情景。当然了,整个一个几何的解体过程,你肯定有你不断试错的过程,对吧?你肯定到最后要少走弯路,当然了,你也有很多种办法,肯定有 几种方法是走的通的,但是千万不要钻牛角尖。那我们看这道题目,初一看我们这道题目很容易走入个误区,是什么?两个线段相等对吗? 然后又是一个等腰直角三角形,那我们第一个感觉会不会去旋转啊,去平移啊之类的。那如果你走了这条路,我不能说是错,那肯定绕了个圈子,或者是走不通这条路。其实这 他是明明确确的是一个是三,边长是三,个个边长都是一,他的比例关系是一比三,所以说他告诉你长度一个三跟告诉你比例关系一比三是不一样的,你的理解就是要从另外一层去理解,所以这个就是标准的一个八字模型。 那我说的八字模型,同学们可以暂停一下,自己尝试一下有没有办法搞定,如果你搞不定,那接下来看我做的辅助线,对吗? 我们说过笔点做平行线,跟 a c 平行,然后延长 a f 交 h, 那 这个线做完了,那我们看啊,整个这个过程中变成了一个八字,对吗?大大的八字,那我们说这跟一比二,所以这是三,整个 b h, 他就等于六,对吗?快点,这个就等于六了啊,这等于六了。嗯,那我们接下来看在这个八字里边, 对吧?那我们说这是一对吗?那整个对面是六,所以 b d 比上 e d 就是 六比一,对吧?那我们只要把 b、 e 求出来,那我们 b、 d 自然是他的七分之六倍的 比,对吧?这个同学们,我建议同学们好好熟练掌握一下八字模型,包括平行线几里边的几个模型的他们整个这个比例关系,然后这个是多少?是占他的百分之比。那你看我这里边举个简单的例子啊, 这个其实在初中里边有一个代数完全可以去证明的啊。来,在这里你看, 我说它的比例关系是 a b b, 对 吧?这一段比,这一段是 a b b, 那 整个这个长度如果是 l 的 话,那我这一段它就应该是 a 加 b 分 之 a 乘以 a, 当然了,下面一段应该是 a 加 b 分 之 b 乘以 a, 这个同学们要熟练掌握啊。 好,有了这个以后,那我们求 b b, 你 有各种办法,有好多种办法,但是肯定要用最快的方法,那这里是二,这里是三,整个 b e 不 就是根号是三吗?对吗? 你不要再走弯路了,不要去证明什么,权当什么乱七八糟的,这个是最简单的了,对吧?那 b、 d 那 就等于七分之六更好,失算好了,问题解决,那同学们看看你能从中受到什么启发。当然了,这个平行线 绝对不是唯一的,我给大家们提个醒,你看过 a 点做 b、 c 的 平行线,这边交过去也行,还有呢? 还有什么?还有我这个是我已经画出来了,在这个样子,同学们可以截图一下。还有什么,你看我做过 c 点做他的平行,你看这边平行过来,这边交过去,对吧?这样也能搞定啊。所以说有很多种办法,但是同学们看了以后你要有 不分门禁的进步,一定要一道题目精雕细琢,你要把这三种方法不断的去想,不断的去完善,你也可以去想想用其他的方法有没有可能性,一道题目够你花四五个小时。
 00:23查看AI文稿AI文稿
00:23查看AI文稿AI文稿中考数学五类几何最值压轴题,全部吃透,稳进班级前三!中考数学五类几何最值压轴题,将军印码最值问题 动点辅助圆类最值!四点共圆瓜豆原理类最值!
39白露学习 00:53查看AI文稿AI文稿
00:53查看AI文稿AI文稿初中数学几何模型就这几类寒假都吃透,中考不丢分!中考常见的几何模型,背长中线模型,基本型中点型中点加平行线型,截长补短模型,借长补短 全等模型,半角模型,手拉手模型等腰等边对角互补模型以及相似模型,这是互补的相似九十度角一线三等角全等的模型,锐角的一线三等角, k 型图钝角的一线三等角 角平分线的重要模型以及全等型。这个包含的话轴对称的模型,垂两边的以及垂中间的 这只罗形将军印马这只模型。胡不归阿世元完整版分享一二三。
56张张. 06:04查看AI文稿AI文稿
06:04查看AI文稿AI文稿这道二五年的中考填空压轴题,当地考生正确率不足百分之一。很多同学啊,看到这么简单的条件,这么简单的图,心里暗自偷笑,却发现读完题只剩了干瞪眼,没有方法, 不管你在草稿纸上怎么摆弄,都无从下手。其实啊,命题人这个题啊,考察的是几何变化,平移对称综合,求最值,别着急,老师,今天啊,就一道题,带你彻底学懂几何变换,求最值,考场遇到直接秒杀!我们来看题, 这个题呢,给的很巧妙哈,它这里说的是 a c 加 cd 是 五啊,就是这一段加这一段是五,然后呢,又给了这一段加这一段是八,然后现在呢?这两个点实际说白了啊,都是动的对吧,求的是 a e 和 b d 相加这两条中间这两条线什么时候有最小值?我天呐,这个题怎么办呀,来跟大家分享一下啊!实际上,大家在初二学全等的时候,我们在学截长补短,大家就应该能意识到啊,我遇到这样的一个条件, a c c d, 你 看 a c c d 这样相加是五, 你要把这个五给他表示出来,必须要干嘛?给他把这一段是给他展开变到这里地撇,对吧?这样的话, a c 加 cd 是 不就很舒服了?能理解,这其实上就是一种什么呀,轴对称思想哎,把它这个三角形对称过来, ok, 同样的道理上面也是一样的啊,就是你现在要求的是这段加这段,我把它对称下去,是变成了这段,就变成了这里,是不是它加它等于八,对吧,而且这里是九十度,就非常好看, ok, 所以 说呢,首先这个题啊,我们第一步要通过对称的思想, 把这个五和八给他表示一下, ok, 来,我画一下啊,把这个三角形呢,给他对称下去,对称到这个地方, e 一 撇。 ok, 那 所以说现在的我们的 b c 加 c, e 就 变成了 b c 加 c e 撇,当然是八,可以吧?就这样一条线啊,当然是八, ok, 与此同时呢,我要把这个造型给它对称过去,是吧?然后呢,这里是 d 一 撇,那我们来标一下啊,就是说原来的 a c 加 cd 就 变成了 a c 加 cd, 撇,当然是五。 各位,现在我们来看到是这样一个图形,这样一根线是五,这样的一根线是八。与此同时呢,你刚才要求的来,各位,你求的是这根线,我现在已经到这里了,对吧?他加上这根线 是他对称过来了,是,他现在求的是他加他什么时候有最小值,能理解了吗?好,这到了我说的第三步,跟大家分享的点,因为图越复杂,很多孩子在考场是越慌越乱的,对不对?所以说呢,我们需要给他抽丝剥茧来,他是我们的 a d 撇, 好吧,然后这个地方呢,是我们的 b 一 撇, ok, 现在求谁啊?求的是各位啊,它加它的最小值,能理解吧?这里是垂直的。好,这个题怎么做到这一步了? 接下来干什么事情呢?继续给他通过几何变换来做一个操作呀?因为已知这个是八,这个是五,而且这里有个垂直。大家想到了什么呀?我是不是可以把这个五和八给他放在一个直角三角形中,通过再次平移 的思路来,我把五给他平移下来,连接他,大家告诉我这是个什么图形? a 一 撇, f 一 撇是个什么图形?平四边形。所以说你要求的这个线段就挪到了这里, 能理解吧?然后本来是这个线段加他的最小值,变成了他加他的最小值,你想想,这里可是五,这里是不是也是五, 对吧?这里是垂直,你平移是不是这里平行也是垂直? ok? 然后现在变成了啥?各位抽丝剥茧了哈,变成了,已知他是八,他是五,这两个点是什么的?因为你是这个线段平移下来的,这个点是固定的,求这里的最什么值?最小值怎么办?两点之间线段最短, 对吧?因为这里只告诉你五,说白了,其实这个点它是动的,可以吗?所以说八五来根号,求一下啊,八八六十四加上二十五,这答案是根号八十九,因此这些答案是根号八十九, 可以理解吗?好,再来给大家分享一个邪修的方法啊,这个方法呢,需要你对于一定的数感和几何图形有有一些感知啊,他告诉你,他加他是几是八,对不对?大家想想啊, 相当于你扯了两根绳,一根绿绳,一根黄绳,长度是固定的,对吧?现在呢,大家去琢磨,他求的是 a 点到这个绳的距离最小,且 b 点到这个绳的距离绳子,对吧?这个距离最小。那怎么办呢?有没有种可能性啊?是我让这个 e 点往上走一走, a 点呢?往回走一走,这根线变短,或者 d 点往外走一走, b 点往下走一走,什么意思啊?来给大家感受一下。其实很多不等式最值的题都是这样的,就是说他俩是一根绳子,刚好取整的时候就说 a 点和 d 点重合, c 点在这 总共是五,我把这个点和他拉在一起,蹬在一起,这里是几?是二分之五。能理解,然后一样的方法啊,你把这根绳和这根绳给他蹬在一起。好,这根绳子这里是几呢?总共是八,那这里是不就是四,对吧?就相当于是 b 点和 e 点重合了, 可以吧?然后你再看你求啥?你求的是 a, e 就是 a 点和 e 点一拉,加上什么, b 点和 d 点也一拉,是不?这根线算两次,这里是直角。来求一下,两倍的根号下它的平方是四分之二十五,加上它的平方是十六,十六的话就是四分之六十四。 答案是两倍的根号下这里是几二,呃,这里出来是两倍的四,出来是二,这里是八十九。看到了没?答案也是八十九。好,这个是谐修的方法,但是这个是实实在在的几何变换。各位,这个题一题多解,你学会了吗?评论区告诉我。
3595郭嘉老师数学思维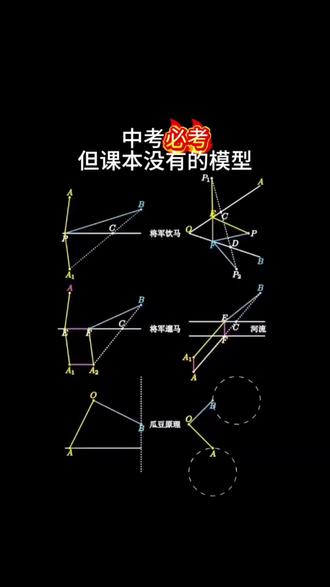 00:49查看AI文稿AI文稿
00:49查看AI文稿AI文稿将军印马模型、将军六马模型、刮斗原理模型、费马点模型、四点共线最短,胡不归模型、垂线段最短 阿,是圆模型,做对应的相似三角形线段最短。就建议孩子是要从初一开始就把这六十八个几何模型,初一到初三常考的各种模型全都学起来,那这里面全都包含了做, 做到大体有思路,小题套模板。你像我们的八字模型啊, a 字模型,备战中线啊,包括我们的手拉手啊,雨伞模型等等,每个模型对应的结论,证明的方法全给你理的清清楚楚。 他每个模型都会有对应的练习题,去巩固你所学的知识。那你不明白的还可以扫码专门看他的视频讲解,掌握了这些解析的模型,就摸清楚他的出题规律了,几何就没有那么难了,所以抓紧时间带走一套回去,赶紧练起来。
2哲同学 05:21查看AI文稿AI文稿
05:21查看AI文稿AI文稿几何里面最最最最容易踩的一个坑,不知道同学们踩过没有?有些同学有可能落概念以后,对中考的某一道题目就有可能踩了一个刻骨铭心的痛。我们说在初中阶段, 在做几何的一个辅助线的时候,往往会有一个矛盾的点,我们看这道题目, 看完题目,我们有没有的孩子会这么去做辅助线啊?说过 a 点做 a e 的 垂线,然后呢?使得 f a f 等于 a e, 那 么这么说的 做 a f 垂直于 a e, 使得 a f 等于 a e, 然后自说自话,这根线一画, f 点就在这个 d 一 上,然后你看看,超级简单了,对吗?然后所有的这两个三角形全等,对吗?因为这个跟这个这个,然后角 脚跟脚相等,对吗?然后两个三角形全等,所以我们要求的这个值就是 e f 值,他如果这是大题目的话,你做完五分钟得分零,对吗?为什么?因为我说你做垂直跟 d e 相交没问题, 相交使得焦点是 f, 那 是没问题的,但是你不能说又要相交,又要 a f 等于 a e, 还要垂直,你无法做到。同时当然了,你也可以说我在这个 不垂直,我找一个,在 d e e 上找一个点,使得 a f 等于 a e, 那 也没问题。同学们不知道能不能在逻辑上面搞明白这个问题,对吗?好了,那我们现在所有的这道题目的 贞洁就在我又要使这个 f 点落在这个上面,又要垂直,又要 a f 等于 a e, 那 实际当然是的确是刚好这个几个条件都能满足的。那我们到底应该怎么做呢? 这个其实就用到了我们在初中阶段最最最最不愿意去用,但是有的时候逼不得已用的一种方法, 三点共线。那我们来看这道题目,我的做法是这个样子的,你看啊,这样的话有没有漏洞?同学们可以一起一起讨论一下啊?如图, 我说我做 a f 垂直于 a e, 使得 a f 等于 a e, 但是这个 f 点不一定在 d e 这条直线上,我是没说这个 f 点在 d e 这条直线上,对吗?那这样的话有没有问题啊?你看我这样弄完以后整个连 连接 d、 f, 对 吗?那显然这个三角形 a、 f、 d 全等于三角形 a、 b、 b, 看看同学们这个有没有问题,因为什么我做的这个是这个跟这个相等,然后呢?当然了,这个是直角对吗?所以这个角跟这个角又相等,所以边 角边对吧?这个边角边他们两个全等是一点问题都没有啊?一点问题都没有好证明好以后,全等以后,那显然因为这个角等于一百三十五度,对吗?那这个 a、 f、 d 也是一百三十五度。 有了 a f、 d 等于一百三十五度以后,我们又说整个这个我做的这个过程中, a 做的这个过程中, a、 e、 f 它是一个等腰且直角的三角形,对吗?所以 a、 f、 e 是 四十五度的。 有了这个以后,我们再说能证明 d、 f、 e 三点共线, 三点共线有好几种办法,对吗?在几何里边,在解析几何里面可以用两两的斜率一样,或者是用两个,有好多的办法啊,比如说我还有一个,就是两个边加起来等于第三个边 也是三点共线,我用到的是这三个点,我这个角加起来是一百八,也能证明他是三点共线。有了三点共线以后,那我们就说 f 点其实就在 d 一 上面,那所以我们要求的 这个东西, d e 减 b e, 那 自然而然,那它就是我们要求的 e f, 那 e f, 当然啦,它就是 a e 的 根号二倍,因为它是等腰直角三角形嘛,那 a e 等于四,那 e f 就 出来了。所以同学们看看整个这道题目,我真要证明有没有瑕疵, 如果有瑕疵,你认为有瑕疵,可以在评论区里跟我跟我跟我讨论。当然了,看看这道题目能不能跳过用三点贡献证明,用其他的办法,大家可以充分发挥自己的想象力,聪明才智,一起在评论区我们讨论一下。
 00:40查看AI文稿AI文稿
00:40查看AI文稿AI文稿初中几何是不是让你特别头疼?看到复杂图形就发蒙?那你真可以看看这本初中几何模型,大钱他把初中几何那些难题,嘿嘿,全都给你总结成了八十一个经典模型, 什么八字模型,飞镖模型,手拉手模型,每个都有图解,有证明,还有配套视频讲解, 简单题直接套模型,秒杀复杂题,教你一步步拆解,转化成熟悉的模型。我翻了一下,它从基础到综合全都有题型,覆盖特别全。几何要是能吃透这些模型,真的能轻松不少。
 01:46查看AI文稿AI文稿
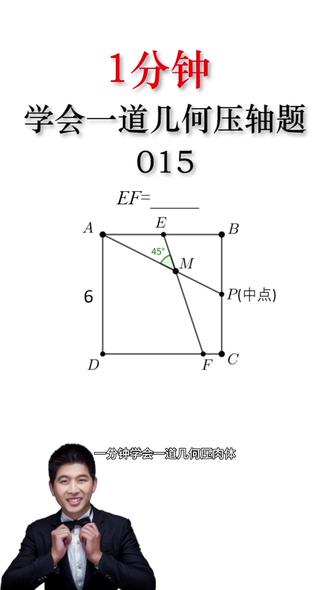
01:46查看AI文稿AI文稿一分钟学会一道几何压轴求线段 e f 的 长度,这是一道填空题,我们可以用一二三四五模型啊, 快速的出答案。那我们先来介绍一下一二三四五模型,如果他按二法等于二分之一,他按贝塔等于三分之一,那么二法加贝塔就等于四十五度。哎,这就是经典的一二三四五模型,这个角在这个位置啊,不太好处理,我们给他移动一下, 我们可以过点 a 去做 e f 的 平行线,那两直线平行内错角相等,所以呢,这个角就等于四十五度。那因为这条线平行于这条线,这条线平行这条线,所以这是一个 平行四边形,那平行四边形对边相等啊,所以 e f 就 等于 a g, 那 要想求 e f 的 长,其实就把 a g 的 长度给求出来就可以了,我们把没用的线都去掉。如果这个角是二法,这个角是贝塔,那么二法加贝塔应该等于九十度,减去四十五度等于四十五度,满足这个条件。 在这个直角三角形中,碳二法等于对边比上邻边,那它的对边呢?就是这个正方形边长了一半,也就是三, 那 ab 的 长度呢?是六,所以探二法等于三比六,也就是二分之一,那很显然满足这个条件,那剩下的这个条件也是满足的,那就说明探贝塔等于三分之一。在这个直角三角形中,探贝塔等于这条边比上六, 那么我们就可以求出 d g, 这条边的长度就是二。那在这个直角三角形中,我们通过勾股定律就可以把 a g 求出来, a g 的 长度就是 e f 的 长度。
58潘小童讲数学 03:07查看AI文稿AI文稿
03:07查看AI文稿AI文稿假期提升计划之第三天,来告诉我,是不是一遇到这类带系数的 pa 加 k pb 最小值的问题,总是傻傻分不清楚, 什么时候用葫芦龟,什么时候用阿士圆,做一次错一次,今天我用三分钟带你彻底搞明白它们的区别。首先来看第一个 pa 加 pb, 此时 k 等于 e, p 在 直线还运动,这是非常典型的将军已满的问题。我们只需要做定点 a 或 b 关于直线 m 的 多线点 b 撇,同时利用两点之间线段最短连接 a b 撇, 当前仅当 a p b 撇三点共线式取最小值。 接下来看第二,此时 k 等于二分之一,不等于一动点 p 在 直线上运动,这就是典型的弧不规的问题。 我们需要在 bc 下方以 b 为顶点构造一个角,使这个角的正弦值恰好等于二分之一。也就是我们只需要在 bc 下方做一个三十度的角, 同时过点 p 做 b d 的 垂线。根据三十度角所对直角边等于斜边的一半,此时我们可以得到 p e 等于二分之一。 p b 问题,即转化为 p a 加 p e 的 最小值。当解,仅当 a、 p e 三点共线时取得最小值 计算的时候,我们只需要在红色三角形 a b e 中利用特殊三角函数值可求的 a e 长为三倍。根号赛 来看第三种情况,此时 k 等于二分之一,不等于一,但是点 p 在 圆弧上运动,那么它就不是琥珀规问题,而是 r 是 圆问题。 根据题目告诉数据,我们需要在 c b 上取一点 d, 使得 c d 等于一。接下来连接 p d, 根据两边对应成比例且夹角相得,我们可证出两个四点形相似且相似。比为一比二,也就是 p d 比 b, p 为一比二,那么 p d 就是 二分之一。 p b 问题即转化为 p a 加 p d 的 最小值,当前仅当 a、 p d 三点共线时取最小值,这个最小值就是线段 a、 d 的 长度,我们只需要在三角形 a、 c、 d 中利用固定进行求结即可。 笔上就是这三类模型的区别,需要注意的是,在解决这三类问题的时候,我们需要用到的竖斜思想为画折为直两个原理,垂线段最短,两点之间线段最短。 不论模型如何变化,我们一定要注意思维的发散性、拓展性,同时还要深入思考,将所学知识灵活运用,举一反三,搞定收工, so easy!
249初中数学王老师🧑🏫 00:52查看AI文稿AI文稿
00:52查看AI文稿AI文稿一秒看懂园内最直 初中几何,一旦掌握了模型,就像打通了任督二脉,数学拿满分都有可能。 就用一本的几何模型,他把初中三年必考的四十二个几何模型都总结好了,像阿史源模型、将军印马模型、 垂美四边形费马点模型等等,每个模型的结论是什么,证明过程怎么写,怎么套用到真题里,全部整理的清清楚楚,让孩子把它吃透。遇到选择填空题,就能直接套用结论写出答案,看不懂也没关系,扫码还有视频讲解, 学完再做对应练习,有学有练才能更快掌握。配套的还有一本函数和应用题,让孩子把它们都吃透,初中三年的数学都不用愁。
 06:03查看AI文稿AI文稿
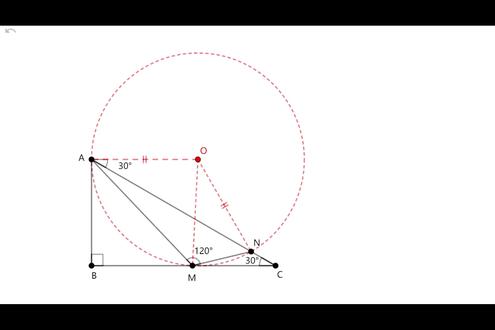
06:03查看AI文稿AI文稿一道难度非常大且趣味性非常强的一道好题目。我们说在初中阶段几何里边,你如果有看到一道题目,想了很多办法,一直想不出来的话, 你千万要记着留的最后一招就是隐形员,我也讲过隐形员的好多题目,但是这道题目我觉得是一个非常有难度的 隐形元的问题,不告诉你,你根本想不到是一个隐形元,那我们来看这道题目。其实看完这道题目,我有类似的一道题目,就是中间 a、 m、 n 是 一个直角三角形, 在这那道题目里面,我也是用隐形元的方式去做的,因为什么?因为它是个直角,特别让人一看就能想得到是一个直径的一个圆,那在这里一百二十度, 他这道题目就出的非常巧妙了,对吗?当然了,我们说那个直角的话,我们可以用代数的方法,也可以去解决,但是这道题目我去尝试过用代数,那在这里边,嗯,就要用到高中的这种三角和差公式比较麻烦, 那用几何的方法引擎元,那就非常好玩。那我们首先读完题目来仔细看一下,首先说告诉你这个三角形的三条边, 这里边一条边,忘了告诉你,对吧?在这里边我记得好像是 a c, 我 记得 a c 好 像等于四,对吗?当然这个无所谓啊,随随便等于几对吧,只要有个参照物,在在在,在物理里边就说只要有个参照物,那整个图形全部都搞定了,在这里边有个直角,有个三十度,有个一百二十度,题目非常简单, 对吧?你这条就非常简单,就这么点,那你能想到是用什么办法做的吗? 我们说整个这道题目里面有个一百二十度啊,那我们一直所说的共圆问题,共圆问题其实是指三个以上的点共圆,那任意一个不在一条直线的三个点,它都能够成一个圆。所以这个一定要同学们有一个 非常强烈的认识啊。我们说的共圆啊,一般是指四个点, 四点及以上啊,那三个点他自然而然,如果这个三个点不在一条直线上的话,他用随便你哪个三个点,他都是共圆的,对吗?所以说我们在这里,其实 a、 n、 n, 他 就形成了一个圆,他形成了这个圆的圆心,如果在这里的话啊,他的这个圆心角啊, 你觉得是几度?我们说正常这个一百二十度的话,他的圆心要是对着这个,他这个是两百四十度,对吧?所以对应的他的圆对这个圆周角,对的,这个是不叫对的啊,就正对着这个四边形的话,他这个刚好也是一百二十度。 那我们看接下来看这个图,我画画好的这个图,对吗?这个是一个比较一般性的,你看这个圆 o, 对 吗?他整个这里面到了这个 r 是 在变化的,对吧?你在这里, 在这里,我们说整个这个是一百二十度,对吗?那又因为它是两条边相等的,那所以这个就是三十度,又告诉你这个是六十度,对吗?所以这个 o 啊,它的轨迹其实是在和 b、 c 平行的这条线上的, 当然了,你这个 o 可以 跑到这边来,对吗?那这边来的话,它的半径有可能这样半径就大了,对吗?它也能形成一个一百二十度的这个角, 同学们不知道能不能理解?好,有了这个以后,我们就说整个这个 a o 啊,它其实 a o, 其实它就是半径,然后这个也是半径,对吗?那我们说要 a 零 最小,对吧? a 零最小,那其实对于这个三角形来说,我们来仔细看一下啊,仔细看一下,对于你看这个三角形来说, a o m 来说,你看它的三角形啊,这个三十度是定的,那所以我要求 a n 最小的话,其实就是求的是这个半径最小,对吧?那我们这里边有个转换过程, a n 求最小,我们通过这个三角形,我们知道这个角度是不变的, 然后它是个等腰三角形,要求 a n 最小,其实我就只要求 a o 最小就行了,对吧?这个转变一定会。有了这个转变以后,那我们就要去想了,怎么样才能让 a o 最小呢?又要满足这个,又要落到这个 b c 上点,那我们来看一下整个这个动画, 看完动画我们就知道整个这个圆啊,跟 b c 的 关系就两种,一种是相交,一种就是相切,当然相切的时候,显然 看图相切的时候,这个圆的半径就是最小的,那我们在这里如果按照这个最小,如果能够搞明白的话,那我们就知道这个三十度没问题了,对吗?那整个 这个半径,你看这个半径跟这个半径如果相切的话,那这一段这个整个这四,这就是二,所以半径就等于二,对吗? 半径等于二以后,那我们接下来求 a 零好办了吗?好办了啊,来做这个垂线,这个三十度的,这是二,那这个是等于多少?刚好三嘛?所以整个 a 零 的最小值就等于二根号三。整个这道题目非常简单,如果你运用到了隐形元的技巧的话,这道题目计算量几乎很小,对吗? 所以说你脑子里永远要留着几个百宝箱,百宝箱里面藏了好多东西,其中隐形元就是一个。 你一定要在逼不得已没有其他办法的时候,你到这个箱子里去找找,看有没有你的好办法藏在里面没掉出来。好了,这道题目就讲到这里。
 11:27查看AI文稿AI文稿
11:27查看AI文稿AI文稿朋友们好,我是老李,这里是老李的初中数学课堂理数说题,你现在看到的是与老李的原创作品初中数学一盘棋配套的视频课程,视频课程目前已经升级到了九百多级, 与视频课程对应的课间一共有十二个,大家可以截屏了解一下,建议大家听课前下载好对应的课间,对照课间听老师讲课。 现在我们一起学习初中数学一盘棋第十二个作品,剑走偏锋的第三十七集,我们用旋转手拉手模型口诀点睛秒杀一道几何题。 结合图形看题目,四边形 a、 b、 c、 d 中连接两条对角线 a、 c 和 b、 d 说三角形 a、 b、 c 是 一个等边三角形, 角 a、 d、 c 等于三, b、 d 等于五, 让我们求三 d 的 差动,遇到等边三角形,结合这里,他让我们求三 d 的 差动,所以我们锁定这里的三点看一下,在三点处出现了共顶点的等线段三 i 等于三 b, 并且角 a、 三 b 等于六十度。跟着老师一起学下来的话,马上应该想到在共端点的端点处找到第三条线段 三 d, 然后加三 d 顺时针或者逆时针旋转六十度。我们结合题目中的另外两个条件看一下, a、 d 的 长度是一致的, b、 d 的 长度也是一致的,所以我们选择加三 d 绕着三点顺时针旋转到这个 位置,旋转到三 k 的 位置,使得角 d、 三 k 等于六十度。这个时候我们看一下,我们相当于把三 b、 三 b 旋转到了三 a 的 位置,然后三 d 旋转到了三开的位置,整体来看就是相当于把三角形三 b、 d 绕着三点顺时针旋转到了三 i、 k 的 位置,所以自然想到连接这里的三 k, 那 么因为角 b i 三等于六十度,角 d i、 k 也等于 六十度,用这两个六十度的角都加上这里的角 i、 c、 d, 这就是老师的课程中经常讲到和用到的所谓的等角套套。等角,看一下这里的这个角 i、 c、 d 和角 i、 c、 k 这两个角相等,不好意思,秃噜嘴了,应该是角 b、 c、 d。 角 b、 c、 d 和角 i、 c、 k 都等于六十度,加上角 i、 c、 d。 等角套套,等角说的就是这件事情,然后以套出来的一段新的等角为线数,我们自然找到了三角形 i、 c、 d, i、 c、 d 和三角形 i、 c、 k。 等角套套。等角,顺藤摸瓜找全等找相似, 这个时候回头看,让每一个已知条件充分的发挥它的作用。 b、 d 的 长度为五,全等三角形对应边相等,所以 b、 d 等于 i k 等于五, i k 等于五,而这里的三 d 等于三 k, 并且 d 三 k 是 一个六十度的角,所以我们自然想到连接这里的 d、 k 得到一个等边三角形,看一下等边三角形 d、 k 三,这个时候我们看一下 id 三,这个角 三十度,然后这个角三 d、 k 等于六十度,所以六十度加三十度,得到这里的这个角 i、 d、 k 九十度,并且 i、 d 的 长度为三, i、 k 的 长度为四,有固定力,所以 d、 k 的 长度等于五。 三角形三 d、 k 是 一个等边三角形 d、 k 的 长度为五,所以 d 三的长度也是一个五,我们要求的线段三 d 的 长度就是五。 下面我们结合思维导图解析的课间复盘一下解析的思路,在学习与旋转手拉手模型相关的题目的时候,一定要想清楚,弄明白。要想快速的找到解析的思路,我们有两个角度, 第一个角度我们要求这里的第三,结论里边要求第三,而这里的 b、 d 等于五是已知的, 然后结合等边,三角形 c、 b 等于 三 a, 所以 我们可以锁定三角形三 b、 d 加三角形三 b、 d 绕着三点 顺时针旋转六十度,展开你的想象力,加三角形三 b、 d 绕着三点旋转六十度,这样的话三 b 旋转到了三 a 的 位置,三 b 和三 a 是 旋转前后的对应边,而这里的三 d 根据旋转的性质也应该旋转六十度,顺时针旋转六十度得到了 c、 e, 也就是说 c、 b 与 c、 i 是 对应边, c、 d 与 c、 e 是 对应边,所以三角形 c、 b、 d 绕着三点顺时针旋转六十度以后,就得到了三角形 c、 i、 e。 从这个角度想问题,找思路,我们叫做整体旋转,换一个角度,就是我们通过总结发现,只要出现了这样的定角 定比,定角定比的两条共端点的线段,看一下三 a 和三 b 定比,两条线段的比值一比一, 并且共端点定角角 a、 三 b 是 一个定角,那么我们就可以在共端点的端点三点处找到第三条线段, 三 d、 三 d 和三 a、 三 b 就 成一个所谓的鸡爪图,然后把三 d 绕着三点,同样顺时针旋转六十度,得到三 e, 然后共叠两个等角,等角套套等角,顺藤 摸瓜找到三角形三 b、 d 和三角形三 a、 e 是 一段缺等的三角形,两个角度可以说殊途同归,构造出来的都是所谓的手拉手的缺等。更进一步,如果三 b 和 三 a 的 比值不是一比一的话,比如说三 b 比上一个三 a, 二比三,那么我们就将 三 d 绕着三点旋转到三 e 的 位置,并且使得三 d 比上一个三 e 也等于二比三,这样我们就得到一段 相似比为二比三的相似三角形旋转手拉手的全等旋转手拉手的相似。 经过这样的操作,结合其他的已知条件,我们自然想到这里的这个角六十度,加上一个三十度等于 九十度直角三角形。然后 i d 等于三, i e 等于已知条件中的 b、 d 全等三角形对应边相等。根据勾股定律就可以求出 d e 的 长度为四,也就是 d 三的长度为四。最后回过头去看一下,就是 一段等别三角形共顶点的等别三角形构成的所谓的手拉手模型。课后对照这里的思维导图解析,课间认真的去反思和 复盘,搞清楚,弄明白如何从两个角度看旋转。现在我们假设 b、 d 和 i e 的 这个焦点为 k 点的话, b、 d 和 i e 的 焦点为 k 点,我们连接这里的三 k, 并把它 严查。请大家想一下,你能否证明在太点处出现的这六个角都是六十度?六个角六十度六六三百六十度组成一个周角。 看一下这里的六个角都是六十度。我们留为课后的思考题。好了,下课再见!
11初中数学壹盘清 00:25查看AI文稿AI文稿
00:25查看AI文稿AI文稿中考考来考去就是这八大模型,铅笔头模型考了十八次,八字模型考了二十次,手拉手模型考了二十五次,雨伞模型考了十五次,燕尾模型考了十四次,将军营马考了二十三次,照爽闲途考了十二次。中考六十八个模型, 一本书全搞定,一题多解,多题一解,由简到难,带视频讲解,不用担心孩子学不会!
 03:38查看AI文稿AI文稿
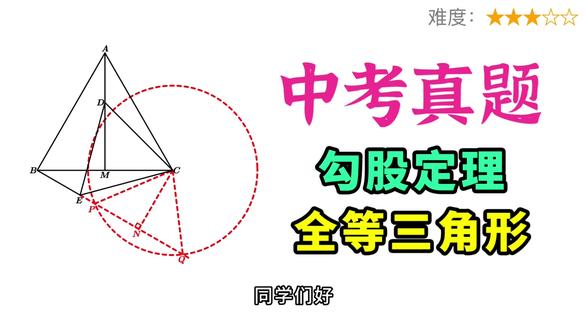
03:38查看AI文稿AI文稿同学们好,今天我们来看一个早年的中考真题。本题考察了全等三角形和勾股定律,对于圆的知识也有所涉及。 如图,三角形 abc 是 一个等边三角形 a、 m 边上的中线动点, d 是 在射线 a、 m 上面,并且和 a 点呢不重合,以 c、 d 为边,在 c、 d 的 下方做等边三角形 c、 d、 e 就是 这个三角形, 然后连接 b、 e。 第一个问,求角 c、 b、 e 就是 这个角的度数,以及 a、 d 这段线段和 b、 e 这段线段的比值。 由于三角形 abc 是 等边三角形, c、 d、 e 这个三角形也是等边三角形,所以我们就有 a、 c 是 等于 bc 的, 而且 c、 d 是 等于 c、 e 的 设角 a、 c、 d 这个角为角一角 b、 c、 d 这个角为角二,那么 b、 c、 e 这个角,它肯定也是角一,因为角一加上角二等于六十度,也就是角 a、 c、 d 是 等于角 b、 c、 e 那 当然就有三角形 a、 c、 d 它是全等于三角形 bc、 e 所以 我们要求的角 c、 b、 e 的 度数,它是等于角 c、 a、 d 也就是这个角。由于 a、 m 是 b、 c 这条边上的中线 三角形 a、 b、 c 是 等边三角形,所以 c、 a、 d 这个角,那它肯定是等于三十度,而且 a、 d 是 等于 b、 e。 那 么当然 a、 d 和 b、 e 这两条线段的比值,它就等于一。 第二个问, ab 的 长度为八,以点 c 为圆心,五为半径做一个圆,那这个半径肯定是小于三角形 abc 的 边长的。然后它与直线 b、 e 交于 p 点和 q 点,让我们求 p、 q 这段线段它的长度, 画出圆 c, 并且找到 p、 q 这段线段的长度,目前看来还缺乏条件,所以接下来我们还需要做辅助线 连接 c p 和 c q, 由于它们都是圆 c 的 半径,所以 c p 是 等于五, c q 也是等于五,我们现在要求的是这个等腰三角形的底边的长, 要想求等腰三角形的底边,我们已经知道腰的长度,还需要知道的就是底边上的高,所以我们过 c 做 b e 这条直线的垂线垂足为 n, 现在需要知道的是 c n, 它的长度是多少。 接下来我们观察 b c n 这个三角形,它是一个直角三角形,并且 bc 的 长度和 ab 的 长度相等,它是等于八。在第一个问当中,我们已经求到了 c b, n 就 这个角,它是三十度,所以我们就可以得到 c n 的 长度为四, 那在三角形 c n、 q 当中,它也是一个直角三角形,并且 c, n 作为一条直角,边的长度为四。我们已经求到了 c, q 是 这个圆的,半径为五, 它作为三角形的斜边。我们也知道了,那么 n q 的 长度就是三,那么同样的道理, p n 的 长度也是三,那么所以 p q 的 长度,那很显然就是这两段加起来,它就是等于六行。有借思无借,这里是无借数学,我是彭老师,我们下期再见。
40无界数学

