八年级下册第四章一次函数的思维导图
粉丝2735获赞1.3万
相关视频
 07:07查看AI文稿AI文稿
07:07查看AI文稿AI文稿大家好,今天我们来讲解一下这个初中数学的一个学习方法,也就是要建立这个思维导图。很多同学呢,在数学的一个学习过程当中, 只顾着刷题,没有进行过总结。所以说我们今天就重点说一下这个思维导图应该如何来建立。首先第一点,这个思维导图他应该包括两个方面, 第一个方面,也就是这个知识点的一个总结。然后第二个方面,也就是简题技巧,或者说简题方法的一个总结。特别是在初中阶段,这个几何题很多, 他涉及到的这些如何做辅助线,那你这些如果不进行总结的话,你在考场上你是想不出来他应该如何做辅助线的。比如说我们平时总结的时候这简题方法,比如说你看到这个终点,那应该想到有有些长的一些做辅助线的一些方法,比如说背长中线法呀,或者说这个呃 三线火呀这些。那我们平时在做题的时候就可以把它进行一个总结。好,我们今天呢就主要讲解一下这个知识点如何总结。我们以这个依次函数为例,因为这个依次函数呢是我们在初中阶段第一次接受这个函数,所以说可能很多同学呢对这一章的一个学习,他有一点模糊。 好,我们先来看一下。首先这个依次函数我们在课本上第一讲,他是首先介绍一下这个函数的概念,所以说我们先把这个函数先把它写在这里。 那我们学习这个函数的目的是什么呢?因为这个函数他研究的是一个变量,也就是说我们处在的是一个变化的世界,变化的世界,而我们要对这个世界进行研究,那就需要建立一个模型。好,这个模型呢,当然有很多,而我们现在初步 学的呢,就是以这个函数,这个模型。好。然后所以说我们可以先这样给他做出来。好,做出来以后,那首先这个函数我们学习一个知识点。首先第一步应该要了解他的是什么了,了解他的一个定义,或者说他的一个概念。 好,那你那你做思维导图的时候,做到这一步,也就是定义和概念的时候,那你就可以在头脑当中回想一下自己能不能够回忆起来,如果说不能回忆起来,那这个时候你就需要翻书来看一下了。 好,然后函数的定义和概念学完以后,那我们第二步就是说函数,从书本上来说,他给出了哪些表示方法, 写到这个表示方法的时候,也要自己回忆一下,看能不能回忆起来。好,我们查含 速长的一个表表示方法呢,他就是以下三种,第一个就是列表法,然后第二个是减息法, 第三个是图像法。也就是说通过这三种方式,他都可以来表示我们的一个函数。好,函数过了以后,那就是我们这一张的一个内容了,就是依次函数。 那同样的,我们在学习一个新的知识点的时候,首先还是要先了解一下他的一个定义和概念。 好,一字函数的定义,它是什么?也就是说一般形式为 y 等于这个 k, x 加 b, 然后 k 或 b 都是常速,并且 k 不等于零。好, 这个时候我们就称之为他为一次函数,当特别的时候,也就是当这个 b 等于零的时候,那他就是一个正比量函数,也就是正比量函数。他应该是一种特殊的一次函数,他也是属于这个一次函数里面的内容。 了解完这个定义以后,那第二步这个依次函数很重要的一点就是要了解他的一个图像。然后第三个还有就是这个他性质 好。那这个性质是怎么得来的呢?他是通过这个图像进行过推导出来的。也就是说,比如说这个,我们知道当 k 大于零的时候,他的一个图像的一个方向应该是在这样的一个方向。 那同理,那如果说这个 b 大于零的时候,我们知道 b, 它相当于是有歪轴的焦点,所以说 k 大于零, b 大于零,那 他的一个图像大致就应该是这样的。所以说他,我们就可以知道他经过了哪些象限,也就是一二三象限。那你通过这个图像可以推导出这个性质。反过来,那你通过这个性质,那你也可以大概推导出这个图像。所以说他们是一个互相推导的一个关系。 好,这个是第二点。然后我们通过这个函数会进一步干什么?进一步会再认识一下这个方程, 通过函数对方程的进一步认识,也就是再认识。而我们在书本上呢,这 这几张涉涉及到的内容主要就是什么呢?这个函数与一元一次方程,还有一元一次不等式或二元一次方程组。比如说这个二元一次方程组,我们在之前的学习当中,主要是通过消元来减这个二元一次方程组, 那我们学了函数以后,还可以通过函数的图像来找他们的焦点,把这一个二元一次方程组剪出来。好,这一个方程呢,那我们也可以通过这个图像来进行一个表示。好。然后这个方程和图像那就是涉及到我们的一些具体的应用呢, 那应用包括哪些方面呢?我们在平时做题的时候就可以进行一个总结。首先比如说我们平时在做题的时候,经常会遇到这个依次函数与这个几何问题进行一个结合, 比如说于我们的四边形,然后还有三角形这些结合。然后还有什么呢?一些应用题,这应用题相当于就是与我们的这个实际问题结合,实际问题相结合。那这样的话我们来看一下实际问题结合。那我们我们再通过函数对这个实 问题进行一个方案的一个选择,也就是选择一个最佳方案,最佳方案,那这个最佳方案实际上就是我们刚才提到的我们解释这个变化事件,或者说我们在这个方案当中选择最好的一点。好 好大概啦,这个就是我们依次函数这一章的一个思维导图。所以说我们在平时学习的时候呢,就是要通过建立思维导图来回忆这些知识点,比如说他的概念呀,还有定义呀,还有这些图像啊性质,我们在做的时候就要在头脑当中进行一个回忆, 如果说回忆不出来的时候,那那我就需要我们再一次翻书。同时我们在做的时候,我们不仅是回忆书本上的概念,比如说这个回忆概念的时候,那我们也要想一下这个概念他一般会涉及到哪些题型。比如说他有可能给你画出 图,一个图,问你这一个图形他是不是函数,那我们就要根据这个概念来进行理解。当然他也有些是写出的这种减息式,比如说他写一个 y 的绝对值等于 x, 那问你是不是这个函数,那我们同样要根据这个函数的一个概念进行一个判断。 所以说我们在回忆的时候,不仅是回忆这个书本上具体的这个概念或者定义,同时我们还要回忆他这个知识点涉及到的哪些题型。
2三年之旅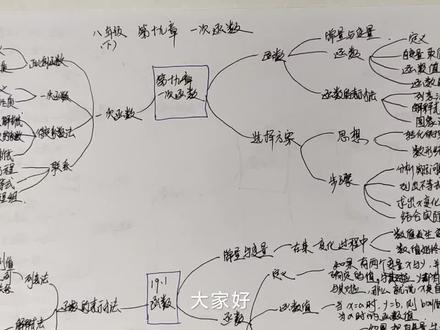 02:19查看AI文稿AI文稿
02:19查看AI文稿AI文稿大家好,我们今天来讲解一下八年级下册第十九章一次函数的思维导图,这一张里面呢,他是这个整个八年级下册的重点内容哈,而且是难点内容。好,我们来看一下 第一个一次函数啊,他这个定义他是怎么样的呢?好,第一,第二个就是说我们学习一下函数啊,他是表示方法,他有列表法,有解释式法,还有图像法,有三种方法哈去表示,一般来说, 好,第二个一次函数,一次函数它有一种比较特别的,就是正比例函数啊,当它这一个 y 等于 k, s 加 b 中的 b, 它等于零的时候,就是正比例函数了, 他这个图像,他的一些特点,还有一次函数啊,形如 y 等于 k, 十加 b 这样子的函数哈,这个 b 等于零的时候,也就是刚才说的正比的函数, 那么它的图像,它的性质就是说这个 k 啊,它大于零的时候,那么这个 y 就随着 s 的增大而增大,但是这个 k 啊,它是小于零的时候,这 y 随着 s 的增大而减小。 这里要注意啊,特别的这里啊,他这个联系啊,就跟这个一元一次不等式,还有一元一次方程他的联系啊,啊,这个二元一次方程组,他们这个组合在一起,就是说他们两个啊,这个一次函数,他们的这个焦点啊,就是可组成二元一次方程组了。 好,第三个选择方案,这里是不是我们会选择一些最优的方案啊?他的步骤, 这是去分析实质问题中的这个建立这个函数它的模型哈,这个列出不等式或者方程,去求出这个 s 变化时候, y 的它的大小,结合实质去选择最佳方案,这里重点是一个思想,是怎么思想呢?转框的思想,还有就是比较这个函数值哈,解方程 在一个就是塑形结合思想,塑形结合思想,在我们这一个整个初中阶段呢,他都是比较重点的,而且是难点,但是却一些抽象的问题哈,他就是把这些变成具体化的啊。好,今天的这一个一次函数的讲解就到这里,谢谢大家。
12汤米讲数学 01:43查看AI文稿AI文稿
01:43查看AI文稿AI文稿大家晚上好,在直播的最后这个时间里呢,给大家小介绍我们今天讲解的内容,今天讲解的是第十九章一次函数,在这里我们会学到的有函数的定义,还有一次函数的他那个定义解释是还有我们的那个选择方案。 好,带着大家的话就是熟悉的一段我们这个书本的例题, 书本讲解完以后呢,就到我们示威导图的讲解。好,有我们这是函数的话,他那些定义的意义,意义,还有函数图像啊,他有个步骤列表,还有描点,还有连线, 还有我们的几个方法,有列表法,解释四法,还有我们的图上法,各个函数那些图上的他的 记忆图,还有我们的那个函数与一次一元,一次方程跟那个不等式的它的关系来解决。 四位导图讲解完毕以后呢,就到我们基础过关时时期的训练。好,在这里的话我们主要是 想想了一下选择题,这里的话有第七题的话,这个比较有意思,在这里的话我们要去跨这个图啊,然后就是根据这个含义的话,先把椅子的图上跨出来,然后再去找我们的那个条件。 还有第八题这里的话,他他会给一个数据的话,我们去找一下其实有四种的那个情况,这里我们这是挑选的话,其中只有图上只有一种是符合的。好,今天的讲解就到这里,感谢大家的收听。
24汤米讲数学 14:50查看AI文稿AI文稿
14:50查看AI文稿AI文稿大家好,今天的话我们来学习一下一字函数的图像,那么图像呢?在我们解题过程中呢,其实是至关重要的,如果说能够学会图像的话,那么解决很多的问题都是信手拈来。那么我们就今天来看到我们 第一个环节,在下列函数中, y 等于 x 的平方减三和 y 等于二 x, y 等于 x, 分之四与 y 等于二减五 x。 哪些是依次函数?我们知道 我们依次函数是 y 等于 k, x 加 b 的形式,然后 k 是不等于零的对吗?如果 b 等于零, 立否? b 等于零,那么说 y 等于 k, x 就变成了依次 正比例函数,对不对?那首先我们来看到一次,你看首先他是二次不对,那么他是不是正比例函数呀?那么这个是不是应该是反比例函数?然后第四个的话是不是一次的函数呀? 第一题是个二十,那第二个只有二,那么他说函数有哪些表示方法?是不是有图像法,列表法以及关系式法, 那么他们之间有什么联系呢?我们看三种方法是可以相互转换的。好,他说你能将关系式法转化为图像法吗?什么是图像法?那么一个问题对不对? 那么现在我们来看到我们要画出下面正比例函数 y 等于 rx 的图像,那么这个图像我们应该怎么去描述呢?或者说他有没有一个流程可以参考? 当然肯定是有一个作图的一个步骤。好。那么现在我们来看到第一个是干嘛呢?列表,列表怎么列呢?首先我们看到一个是 x, 一个是 y, 那么我们取这里的话一般是怎么样呢?取一个零点, 就是取圆圆点那个零啊,当 x 等于零的时候,然后 y 等于多少?你看然后是不是向两边取啊? 好,最后我们得到这些点的话,我们要干嘛呢?是不是 变成列表法?那么现在我们叫描点。什么叫描点呢?就是以表中各组对应值作为点的坐标,在直角坐标系中描出相应的点。你看我们把直表坐标系描出来。好, 你看这描述了点呢?然后我们进行下一步是不是连线,把他们连起来。这就是我们画的图,并且要写上他的那个表达式。所以说我们可以归纳一下画函数图像的一般步骤是不是一是列表,二是描点,三是连线,对吗? 那么现在我们来看到他说根据这个步骤画出 y 函数, y 等于负三 x 的图像。同学们可以在自己的那个草稿纸上尝试一下这个图像好吗? 那么来看好,我们就可以很快速的得到 y 等于负三 x 图像。那么他们这个你看 y 等于二 x 和负三 x, 他们的图像是不一样的呀, 你看有什么特征对不对?一个是向上走,一个是向下走,对吗? 我们可以得到 y 等于 k x, k 是长数,且 k 不等于零,是一条经过圆点的直线。你看经过的象线。 呃,当 k 大于零的时候,我们是不是可以经过一三项线? k 小于零的时候,我们经过二四项线。那么这个的话是在我们以后做题中呢?是很普遍的。所以说我们一定要知道他为什么过一三,为什么过二四好吗? 那么怎么画正比例图像最简单呢?为什么好?其实我们还有另外一种方法,叫两点做图法。由于 两点确定一条直线吗?画正比例函数的图像时,我们只需要秒点零零和一跟 k, 你看我把一跟带进去,是不是他 y 就等于 k 啊?他肯定过一跟 k 这个点,所以我们直接连线就可以了。 他说用你最简单的方法画出下列函数的图像,那么我们最简单的画是不是你看这个就很简单哈,是不是两点画图法呀?是不是直接画出来了,对吗? 是不是就比较简单了,对不对?好。至于这两种方法呢?第一种我们是一定要掌握的,第一个是不是列表,第二个是瞄点,第三个是连线,有没有问题? 那么现在我们来看到我们的立体环节,他说已知正比例函数图像 y 等于 m 加一乘以 x 的 m 的平方,他的函数过几上限对不对? 那么我们知道他说正比例函数,正比例函数,那么我们知道他的指数肯定是一喽。首先我们 要干嘛呢?是不是第一要写解对吧?这第一步。然后是不是根据 m 的平方等于一,我们就可以推出 m 等于正负一,然后 m 等于正负一的话,前面的系数不能为零哦。所以说我们是不是 m 就等于多少啊,是不等于一了。所以说他是 y 等于二 x, 你看他这个 k 是大于零,我们知道 k 大于零的情况,他是不是一条爬坡的线呢?是经过一三向线,所以说他的图像是不是经过一三向线呢? 然后我们可以看到哈,首先是不是 m 的平方等于一,而且 m 加一不等于零,这也是少了一个空好吧, 说 k 是要大于零的,然后我们可以得到过一三上线。那么第二题他说已知正比例,所以说你看正比例函数对不对?那我们 k 加一,首先我们就可以得到一个隐藏条件, k 不等于负一。然后他说落函数经过一三上线,一三上线的话,我们 k 加一是不是要大于零,那么 k 是不是要大于负一,对吧。好。所以说我们第一个空是不是可以得到 k 大于负一。 那么第二题若函数图像经过二次这个点,那么你既然经过这个点的话,那么你肯定会满足这个函数关系的事。所以说我们带路两倍的 k 加一是不是要等于四呀?那我们可以知道 k 加一就等于二,那么我们 k 是不是等于一,所以这个就比较简单了对吧。 所以说我们就是说如果你经函数图像经过这个点的话,那么他一定是会满足这个关系式的 好。那么现在我们看到编试啊,他说当 x 大于零时, y 与 x 的解析是是 y 等于二, x, 当 x 小于或等于零的时候, y x 的函数解析是他说这在同一大字尾。我们来看一下哈。哎,怎么没有图呢?那我们就来看一下喽,我们就直接自己画好吧, 我们刚刚是不是有学过两点画图法呀?那么首先我们看 x 大于零,好,那么就是这边他是,那么他一定会经过一二这个点。对, 这是一了,是二,所以 他肯定会经过这一个点对吧?他说当 x 小于零时, y 等于负, x 负的话,负一好负二。所以说他是不是也会经过这里啊,把他连起来就好了, 出一个这样的图像啊。就说虽然说这道题没有图像啊,但是我们需要自己能够把它给画出来,其实还是比较简单的。然后我们看到第三题,他说在同一只有 直角坐标系内画出正比例函数, y 等于 x, 然后 y 等于三, xy 等于负, x 和 y 等于负四 x 图像。这个图呢,就让同学们自己去 画喽,对不对?你看 y 等于 r x 对吧?好,这是 y 等于 r x 图,你看我们怎么去画他的? 你看这个当 x 增大的时候, y 值也是增大的,有没有发现好,那么他说 y 是为 x 增大而增大。那么我们看到第二个图, y 等于负的。那么你看 他这里的话是不是 y 随着你看 x 是增大的,但是 y 是慢慢减小的,所以说是不是当 xk 小零, y 随着 x 增大而减小, 能明白吗?所以说我们就可以总总结出一个结论是什么呢?就是在正比例函数中有没有发现这个是前提, 如果没有这个前提,那么他一切的结论都是错误的。那么当 k 大于零时, y 随着 x 增大而增大,当 k 小于零时, y 随着 x 的增大而减小。 这个时候呢,我们就可以判断他们哪个值跟大呀?或者给你两个点判断他们的大小关系好。那么现在我们来看这个 正比例函数, y 等于 x 和 y 等于三, x 中随着 x 增大, y 的值都增大,其中哪一个增加的更快呢?你能说明其中的理由吗? 对不对?这个题目呢,我们就当成一个课后作业,然后自己可以去画一下这个图,然后我们就可以看得出谁更大,然后就可以得出自己的规律了。 向我们看 k 的绝对词越大,直线就越陡,直线就越靠近歪走,相应的函数值上升或者下降的越快。我相信这样结论型的东西肯定是没有说自己总结出来的好嘛,所以说你同学们可以自己尝试一 下。好,我们来看到这里。当 k 相等时,图像是关于坐标走势对称的,有没有发现呢?那么两种颜色的就是同一条直线哈。 好。那么现在我们来看到这道题,他说呃,已知 k 大于零,对不对?他说两点, x 一小于。我们知道 k 大于零,是谁在 x 的增大而增大,那么 x 二更大。所以说我们就可以得到 y 一, y 一是不小于 y 二呀。那么第二题 证明函数 y 等于 k e x。 那么我们是刚刚有讲到,就是说他的 k 的绝对值越大的话,是不是升上升或者下降的越快呀。所以说我们是不是可以得到 k 一是大于 k 二。 那么第三题他说已知呃,这个过这个点对不对?然后且 m, 且 y 随着 x 增大而减小,那么我们可不可以得到一个。其实通过这一句话我们就要得出一个什么呢?是不是我们 m 是小于零的呀?那么他又经过这个点带路呗。 m 的平方等于四,然后 m 等于正负二,因为他 m 要小于零。所以说我们就可以推出 m 是不是等于负二。除了这道题是不是做出来了。好,我们来看到步骤哈。首先解 是不是 m 等于负二呀?其实这个还是比较简单的哈。然后我们看到这一题,他说下列图像 y 可能是函数 y 等于负 x。 首先我们来看第一个肯定不对,因为他远点都不过,那么 第二个的话是不是他的 k 是小于零的,然后他是随着 x 增大而减小,所以说我们是不是答案就可以出来了?第二个选项。那么第二题正比例函数 y 等于 k 减二 x, 当 x 增大时, y 随着 x 增大而增大,那么增大和增大说明 x k 减二是要大于零了。 所以说是不是 k 大于二啊,有没有问题?所以说我们这题的答案可以选择到三 c 选项。好,那么看到这个题,他说经过第几项线,过 什么点什么点,对不对?好,这题的话我们是不是可以知道他肯定 k 小于零嘛?首先我们知道 k 小于零,是不是经过二次上线了,然后经过零零这个点,然后经过一和负七, y 随着 x 增大额减小,对吗? 让我们看到第一题,他说函数经过一三上线,一三上线的话,我们知道 k 是大于零的,所以说二 m 加四要大于零,那么 m 是不是大于负二? 好,所以说第一题是把 m 大于负二,他说减小,那么反过来就是 m 小于负二。他说要经过这个点话,那么我们把把这个点带入了 rm 加四是不是乘以二等于十,然后我们就可以得到 rm 加四就等于五, m 是不等于二 c。 最终我们是不是可以得到 m 等于二分之一啊?那么来看到这个比 k 的值。呃,其实这里比 k 的值需要注意的一个就是说什么呢? 呃,我们看 k 一跟 k 二。首先我们来看 k 一, k 二可以跟 k 二,谁下降的更快呀?是不是?我们可以知道 k 一的绝对只 是大于 k 二的绝对值对不对?然后他们是减减小的,所以说我们可以得到第一个是不是 k 二更大,这里比较关键哈,因为他绝对值大嘛,负数的绝对值大,所以说他的值反而小啊。第二个三跟四的话,那么他们就是四大于三咯。 用不等号我们去连接,他说一二三四就。那我们你看这个是正的,这个是负的,不就直接就可以连起来了对吧?这就比较简单哈。 好。那么现在我们看到第五第六题了。已知。嗯。耗油量是每千米一十五升,所使用的汽油是五元每升,写出汽油在行驶中,你看 所耗油费与行驶 x 之间的关系对不对?耗油费那么首先我们可以看怎么他说 x 对不对。 那么我们可以这样算呗,是不是一百的话我们就乘以十五,那么 x 除以一百乘以十五,然后再乘以五啊。那我们可以这里可以约下分对最后的结果的话是不是二十,这里是三,然后这里的话约个五是不是四, 然后就没,是不是等于四分之三 x 啊,对不对? 好,现在我们来看到第二题啊。第二题他说在图像,然后行驶二百二十千米所需要的邮费。好,那么现在我们来看到这个图哈。他当他列出图之后就特别简单,我们带路嘛,是不是就比较简单了,当 x 等于二百二嘛。
 19:50
19:50













