五年级制作风筝数学题怎么解答
如图,四边形 abcd 的对角线相交于点 o。 如果三角形 abd 的面积等于三角形 bcd 面积的三分之一,那么通过这个条件,我们可以根据风筝模型可以得到一个结论 三角形 abd 的面积比上三角形 bcd 呢?它是等于一比三的,它其实就应该等于 ao 比上 co 这个的长度比。那么现在已知 ao 等于二,所以说我 co 呢,就应该是等于六的。 又因因为 do 等于三,所以说我 ceo 应该是等于二倍的 do 的,所以应该存在一个两倍关系。答案是二。各位小朋友听懂了吗?
粉丝996获赞800
相关视频
 02:18查看AI文稿AI文稿
02:18查看AI文稿AI文稿今天我们来复习一下风筝模型。什么是风筝模型?比如说随便一个四边形,那么连接他的两条对角线,上边的三角形和下边的三角形,他们的面积之比就是他们两条斜线的笔。那为什么有这样的这个结论呢?我们可以来证明一下, 假设 a 一比一, c 是三比二,那么我们只要证明三角形 abd 比上三角形 bcd 等于三比二,就能证明他们的面积之笔是两这两条前面的这个笔了。那先标记一下,这里是三,这里是二。 先把目光锁定在左半部,观察一下, abe 和 bce 两个人是等高三角形,他们的头呢共用的是 b, 脚底板都是 ac 这条线上的,所以他们是等高三角形,那也就是说他们的面积 一支笔可以是三比二,那我可以将 abe 设为面积为三, x 对应的 bce 的面积就是二 x, 那么以此类推,我可以把左边也遮住,观察一下右半部分, ab 可以设为三外, ecd 可以设为二外,那么我可以把 abd 改成是三 x 加上三 y, bcd 呢?可以把它用二外加二 x 来代替。 这个时候我们再提取公因数,把三提出来 x 加 y, 再把二提出来 x 加 y, 那么两边同时进行 啊,约掉 x 加 y, 这个操作就可以变成三比二,那么就证明完毕了。如果能学会风筝模型的话呢,做很多这个几何形的时候还是蛮 很方便的。这个风筝模型也叫做烤串模型,我们有一个比较形象化的记忆方法啊。先来说第一个,就是两个三角形的面积之比呢,为甲高之比,因为它是斜线,不是垂直地面的,所以它是假的高。第二个叫做两片肉的面积之比,为穿过的天的长度之比, 把这两个造型给画个圈,那就很像是一个烤串了,所以我们可以用这个烤串的方法去记忆肉的面积之笔,就是穿过的签字的笔。 ok 了,如果能听懂的朋友呢,请记得点个赞,收藏关注我,学习更多数学小方法。
38比老师会数学 02:32
02:32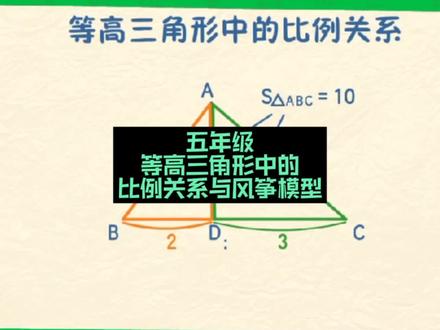 05:03查看AI文稿AI文稿
05:03查看AI文稿AI文稿前咱们讲过这种等高三角形,他们底边的倍数就等于面积的倍数,比如底边是两倍关系,那面积也是两倍关系。 如果把倍数换成比例,那 dc 是 bd 的两倍,就说明 bd 是一份的话, dc 就是两份,所以底边之比是一比二。 同样的面积是两倍关系,说明面积比也是一比二。像这样把倍数换成比例后,里边的比例和面积的比例依然相等。 那如果把比例换一下,结论是不是也成立呢?比如把左右两个三角形底边之比改成二比三,那面积之比是多少呢?底边的比是二比三,这就说明 左边三角形的底边长是两份,右边三角形的底边长是三份,每一份都对应一个小三角形 啊,整个三角形就被等分成了五份,左边三角形占两份,右边三角形占了三份,所以面积比就是二比三,和底边之比是一样的。 这一下咱们就可以确定了,等高三角形中比的比就等于面积的比,这就是等高三角形中的比例关系。 在具体做题时,他还会告诉你整个大三角形 abc 的面积,比如是十,然后让你求左右两个三角形的面积,那你只要把十按比例分配一下就行,就能得到左边三角形的面积是四, 右边三角形的面积是六。好了,总结一下,等高三角形中底边的比就等于面积的比,也就是 s 一比 s 二就等于 bd 比例 c。 现在问题来了, 如果 bd 比 bc 等于七比六,左边三角形面积是十四,那右边三角形面积是多少呢?这个视频我来介绍一下风筝模型, 这是一个四边形,连接他的两条对角线就可以得到四个三角形,依然需要发挥你的想象力,看像不像风筝,所以就叫风筝模型。 方正模型主要研究的是这四个三角形面积的关系,把他们分别继承 s 一、 s 二、 s 三和 s 四,那这四个面积有什么关系呢?咱们先来看上面两个三角形,他俩是等高三角形,所以面积之比就等于底边的比,也就是 s 一比 s 二等于 eo 比 o d。 再看下面两个三角形,也是等高的,所以面积比也等于底边的比,也就是 s 三比 s 四就等于 b o 比 o d。 擦亮你的双眼,仔细观察一下,这俩都等于 b o、 b o d, 那他俩也是相等的,也就是说, s 一比 s 二,就等于 s 三比 s 四, 这就是四边形中这四个面积的比例关系,也是风筝模型的重要结论。进一步呢,利用交叉相乘,咱们 还可以得到, s 一乘 s 四就等于 s 二乘 s 三。再图上来看的话,就是这两个对着的面积相乘,就等于这两个对着的面积相乘。 比如 s 一是六, s 二是十, s 三是九,那 s 四等于多少呢?刚才说了,六乘 s 四就等于十乘九,算一下 s 四就等于十五。搞定, 刚才这个结论说的是这四个小三角形的面积关系,那大三角形和大三角形之间有没有关系呢?当然有, 这俩面积的比就等于 b o、 b o d, 由此我们可以得到 b o、 b o d 就等于六比十,也就 就是三比五。再看左边的大三角形,总面积是六加九,得十五,而右边的大三角形总面积是十加十五得二十五,所以左边三角形 abc 的面积 比上右边三角形 a、 d、 c 的面积就等于十五比二十五,也等于三比五,所以这俩是相等的。 也就是说,左边三角形的面积比上右边三角形的面积也等于 b、 o、 b、 o、 d。 类似的,上方三角形的面积比上下方三角形的面积就等于 a、 o、 b、 o、 c。 好了,以上就是风筝模型的两个结论,现在问题来了,在这个图里有三块面积一只,那剩下这一块面积是多少呢?
186小学思维数学全集 01:40
01:40 03:02查看AI文稿AI文稿
03:02查看AI文稿AI文稿图中的这个图像不像一个风筝呢?园子老师跟大家加一下小须须,再加一根线,是不是特别像一个风筝?那么风筝模型它究竟有哪些特征?今天我们来聊一聊。首先咱们要去解决第一个问题,很多同学他是不理解面积和底边之间的关系, 那么现在请大家把眼光锁定到 abd 这个三角形中, abd 里面有一个 aob, 也就是咱们要研究的 s 一,以及咱们要研究的 aods 二,他们之间会有什么关系?大家去想一想,他们都是共顶点的, 第一个共顶点,由顶点向对边做一条垂直线段,是不是 a、 b、 d 的高啊?对不对?这个高大家去看一下,是不是也是 a o b 的高, 也是 a、 o d 的高,所以这两个三角形它是共高的,这个非常清楚。那如果你非要我把它的算式写出来,那我写一写, s 一等于二分之一的 o b 乘 h, 同样的 s 二,它就等于二分之一的 o d 乘 h, 那么大家去观察一下,如果现在我要建立一个比, s 一比 s 二,是不是也就等于上面的比,上下面的 我们的二分之一全部都约掉了一级高,对吧?所以也就是等于 o b、 b、 o d, 所以这个地方第一个要去建立面积之比,其实就等于对应的底边的比,这个要搞清楚。同样的,我们来想想 s 三和 s 四什么关系? 他们依然是共顶点的这个 c 点,那么由 c 点向对边做垂直线段, 也就是 c、 b、 d 的高,那么这个高既是 o b c 的高,又是 o、 c、 d 的高,依然是共高。所以我们 s 三和 s 四的面积之比,实际上就是底边的 o b 和 o d 的比, 同学们听懂了吗?那么现在请你去帮我观察一下。 s 一比 s 二等于 o b、 比 o d, s 三比 s 四也是等于 o b 比 o d 的,所以通过 o b 比 o d, 咱们都是相同的建立了一个比例,看到没有?那现在我能不能找到 s 一、 s 二、 s 三、 s 四 字之间的关系呢?根据比例的基本性质,外相机等于内相机,所以 s 一乘上 s 四等于 s 二乘 s 三, 这就是风筝模型你要去掌握的一个线索或者是一个要领。好,一定要把这个好好的在草稿本上试一试啊。下一讲我们来讲一讲风筝模型的一些运用。关注言子老师,小牲畜不迷路,拜拜。
1081园子老师 00:44
00:44










