逆等线段求最值方法
粉丝164.6万获赞1637.6万
相关视频
 01:17查看AI文稿AI文稿
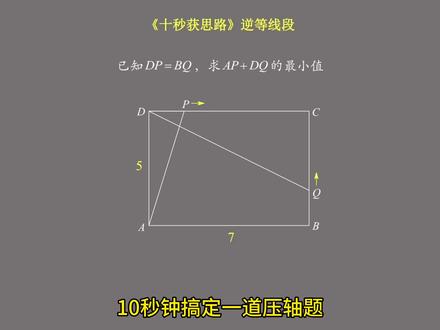
01:17查看AI文稿AI文稿十秒钟搞定一道压轴题,给出一个矩形,一边为五,一边为七。 pq 是两边上的动点,但是不管怎么运动,这两条绿边永远相等。连接 ap, 连接 dq, 求这两条线段之和的最小值。 这个题用常规方法非常麻烦,但如果我们知道逆等线段,那就完全不一样了。如果两条线段相等,但他们既不能构成等腰,又无法构造全等,像这样的两条线段,我们就把它叫做逆等线段。 内等线段的处理方法有很多,但最常见的就是把一条边所在的三角形放在另外一条对应的相等线段上,放完之后大概长这个样子,也就是把这个三角形放到这里。 你让我求 a p 加 d q 的最小值,我偏不,我们把这个三角形挪到了这里,所以 a p 等于 q m, 所以我只要使得 q m 加, 加上 dq 最小就可以了。这就相当于从 d 点出发,经过 bc 上的 q 点,最终回到了 m 点,从一个点到另外一个点,两点之间线段最短,所以我们连接 dm, 当 q 点在这里时,取得最小值, 最小值就是线段 dm 的长度。那 dm 怎么求呢?你会发现,在这个直角三角形中,一边为五,一边等于七加五,根据科普定理,可求斜边等于十三,搞定。
1.6万亮亮巧解数学 04:24
04:24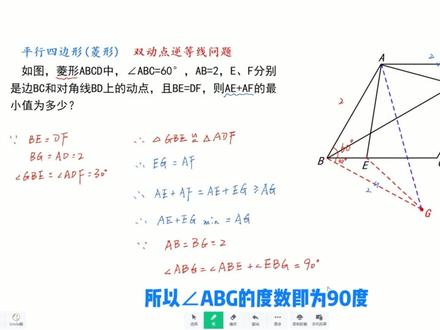 03:20查看AI文稿AI文稿
03:20查看AI文稿AI文稿双动点最直中的逆等线问题,有很多同学不知从何下手,今天我们就用一道题来帮助你掌握 好,我们来看题,如图,菱形 a、 b c d 中角 a b c 是等于六十度的, a、 b 等于二点一和点 f 分别为边 b、 c 和对角线比例上的动点,且 b、 e 是等于 d f 的。问我们 a e 加上 a、 f 的最小值为多少? 我们来分析题目。这道题有一个非常明显的特征,就是在两个动点 e 和 f 的运动过程中,线段 b e 和 d f 的长度他们总是保持相等的,而问题要求的是另两条与点 e、 点 f 有关的线段和的最小值。 这一系列条件的特征既是我们所说的逆等线模型,而解决此类问题的核心思路就是利用已知等长的线段为一边,通过添加辅助 线来构造于目标三角形所对应的一边一角,从而完成边角边全等。把所求两条线段合中的一条进行等长转化,使双动点转化为单动点,实现两条线段的拼接,画散为连,再根据两点之间线段最短来化折为值,从而解决问题。 好,我们带着这个思路来看这道题,因为在点 e 和点 f 的运动过程中, b、 e 总是等于 d f 的,而要求的是 a e 加 a f 的最小值, 因此我们就以三角形 a、 d、 f 为目标三角形,以等长线段中的鼻翼为一条边,构造出一个与三角形 a、 d、 f 全等的三角形, 使得我们构造出的这一个三角形中的一边与三角形 a、 d、 f 中的 a、 f 对应,并且呢,同时又与 a、 e 这条线段共断点。因为是个菱形问题, 所以在三角形 a、 d、 f 中,角 a、 d、 f 即为角 a、 d、 c 的一半,那也就是等于三十度。因此我们对标角 a、 d、 f 在鼻翼这一条线段的下方做出角 e、 b、 g 等于角 a、 d、 f, 也就是等于三十度的, 并使得 b 级的长度等于 a、 d 的长度,也就是等于菱形的边长二。好,此时我们如果来连接 e 级,那我们所构造出的这一个三角形 b、 g、 e, 他是不是就全等于三角形 adf 的?也就是我们通过构造一边一角来完成了边角边全等。那根据全等的性质, 无论点 e 运动到哪一个位置, e 级这一条线段的长度总是等于它的对应边 a、 f 的长度的。这样我们就完成了 a、 e 与 a、 f 的拼接,把 a、 e 加 a、 f 两条线段和转化为了 a、 e 加 e 级两条线段和的问题。而 又因为点 a 和点级均为定点,那根据两点之间线段最短, a、 e 加上 e 级的最小值即为 a、 e 级这三点贡献时,而最小值即为 a 级这条连接线段的长度。接下来就是如何来求 a 级的长度。 我们来看,因为 a、 b 是等于 b、 g 等于二的,而角 a、 b、 g 的度数又是等于六十度的角 a、 b、 c 加上三十度的角 e、 b、 g 之和,所以角 a、 b、 g 的度数即为九十度。 那么三角形 a、 g、 b 其实就是一个等腰直角三角形,而我们要求的 a 级即为它的斜边,因此 a 级的长度就等于根号二倍的 ab, 那也就是等于二倍的根号二, 也就是说 a、 e 加上 a、 f 的最小值即为二倍的根号二。好,逆等线问题您学会了吗?学习的本质是思考。
5043自主学习戴













![[超高频考点]逆等线模型,秒解双动点最值问题 #中考数学 #逆等线模型 #初中数学 #平面几何 #辅助线](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/858cff3a6069046ea40ca61de862ddb2~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079547200&x-signature=X%2FnRs8MAWrvlvkLeiozbUef9f9s%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=2025112704133313426EAC2073FA3345C3)


