粉丝2.6万获赞14.1万
相关视频
 02:00查看AI文稿AI文稿
02:00查看AI文稿AI文稿同学们好,来看一下我们六年级上册个性拓展面第五十八页的内容,第七期计算上环的面积得数,保留两位小数啊,那么上环的面积的话呢?我们啊上环的面积的话呢,实际上就是用我们的 大的扇形的面积去减去小的扇形的面积啊,可以理解,参照我们去学圆环的面积来计算他就可以了。那么大扇形的面积呢?我们都知道扇形的面积 三百六十分之 n 派 r 的平方,对吧? n 是我们的圆心角,那我们大的扇形的面积就是三百六十分之一百二十 派大啊的平方,大啊呢是我们的吧,那我们直接先写公式吧,然后减去我们的小扇形的面积三百六十分之一百二十派小啊的平方。 好在这里面呢,我们把三百六十分之一百二十进行我们的月分化减,最后是三分之一,这时候我们把三分之一派可以提取出来,里面就剩大的平方减去小的的平方了, 到这一步的时候呢,我们再带成数就可以了啊,这时候我们的派就取三点一四就可以了,然后我们的八的平方,七减三的平方, 三分之一乘三点一四, 再乘五十五啊,六十四减九五十五,约等于得出保证。两位小说啊,五十七点五七平方米, 在做这个上环的面积的时候,我们就参照圆环的面积去做就可以了啊。
17暖心1314 20:22查看AI文稿AI文稿
20:22查看AI文稿AI文稿同学们大家好,这节课我们一起来学习圆环的面积。首先我们来回顾一下上节课所学的内容。上节课我们学习了圆的面积,利用减拼法,我们将圆转化成了近似的长方形,从而得出了圆面积的计算方法, s 等于派二的平方。这节课我们将继续来学习圆环的面积。 提到圆环,同学们想一想,在生活中,你在哪些地方见过圆环呢? 比如汽车的轮胎上、救生圈上、光盘上、透明胶带上,再比如像钢管的横截面,像射箭的箭靶等等。生活中许多地方 都可以见到圆环,那么究竟什么是圆环呢?像这样的两个半径不相等的同心圆之间的部分就是圆环,其中较大的圆称为外圆,它的半径用大写字母二来表示, 较小的圆称为内圆,它的半径用小写字母二来表示。圆环就是外圆和内圆这两个同心圆之间的部分。 外圆半径减内圆半径就是圆环的宽度,简称环宽。因此环宽就等于外圆半径减内圆半径。那么怎样在一张圆形纸上剪出一个圆环? 我们可以选择和已知圆相同的圆心位置,再画一个较小的圆,把这个较小的圆剪掉,剩余部分就是一个圆环了。 再来想一想,如果把圆环从中间对折,会出现什么情况呢? 像这样把圆环从中间对折,两边可以完全重合,因此圆环是轴对称图形,除了横着对折,也可以竖着对折。 从图中可以看出,圆环的对称轴经过了外圆和内圆共同的圆心。由于圆环是由两个同心圆组成的,而圆有无数条对称轴,因此圆环 也有无数条对称轴。 在认识了圆环这些形状特征之后,请同学们来选一选下面哪个图形是圆环。 圆环是由两个同心圆组成的,因此 b 选项是正确的。 接下来我们来看一个实际问题。光盘的银色部分是一个圆环,内圆半径是两厘米,外圆半径是六厘米。圆环的面积是多少 有已知信息可以知道,我们要求的就是像这样的一个圆环的面积。该怎样计算一个圆环的面积呢?同学们有什么好办法吗? 想象一下刚才从一张圆形纸上剪出圆环的过程,为了计算这个圆环的面积,我们可以先求出外圆的面积,再从外圆的面积中剪掉内圆的面积就是圆环的面积了。 因此,根据圆面积的计算公式, s 等于派二的平方,我们可以用三点一四乘六的平方来求外圆的面积, 用三点一四乘二的平方来求内圆的面积,二者求差就是圆环的面积了。 在计算时,请同学们注意,在这个算式中,平方运算的运算级比较高,因此要先计算平方,六的平方等于六乘六等于三十六,二 的平方等于二乘二等于四,因此,这个算式就等于三点一四乘三十六减三点一四乘四。继续计算,求出圆环的面积是一百点四八平方厘米。完成答画, 这就是计算圆环面积的一种方法。我们再回顾一下这个算式,如果从简便运算的角度考虑,同学们有什么发现吗? 是的,这个算是符合乘法分配率的逆向运用,因此我们可以把相同的因数三点一四提取出来, 这个算式可以写作三点一四乘六的平方,减二的平方的差,这就是计算圆环面积的第二种方法。 在计算时同样要注意要先算平方,因此等于三点一四乘三十六减四的差,等于三点一四乘三十二,等于一百点四八平方厘米。 对比方法二,我们来思考一下,如果用三点一四乘六减二的差的平方来计算圆环的面积可以吗? 我们对比一下这两个算式之间的区别。在方法二中是三点一四乘六的平方,减二的平方的差, 括号中是先算平方再求差,而在这个算式中是三点一四乘六减二的差的平方是先求差再平方,这两个算式是相等的。 同学们是怎样思考这个问题的呢?我们可以先通过计算来验证一下。 三点一四乘六减二的差的平方等于三点一四乘四的平方,等于三点一四乘十六等于五十点二四平方厘米,显然和我们刚刚求出的圆环面积是不相等的,说明这两个算式并不相等。 我们再从它的实际含义上来了解一下这两个算式之间的区别。 首先来看左边三点一四乘六的平方,减二的平方的差来源于三点一四乘六的平方,减三点一四乘二的平方,它表示的就是从半径六厘 厘米的外圆面积中减掉半径两厘米的内圆面积,剩余部分就是圆环的面积了。再来看右边三点一四乘六减二的差的平方,其实就等于三点一四乘四的平方, 表示的是从六厘米的线段中减掉两厘米的线段,所剩是四厘米的线段,而三点一四乘四的平方就表示以四厘米为半径的圆的面积。现在同学们可以体会到这二者之间的区别了吗? 因此,在计算像这样六的平方减二的平方的运算时,请同学们要小心,一定要先算平方再求差,而不能先求差再平方,二者是不相等的。 好了,回归到我们本道解决问题上来,我们有两种方法可以求圆环的面积。第一种方法就是直接利用外圆的面积减内圆的面积。第二种方法就是根据乘法分配率将相同的因数三点一四提取出来, 先将除三点一四以外的部分进行运算,再和三点一四运算,这样计算比较简便。 我们来总结一下圆环面积的计算方法。圆环的面积就等于外圆面积减内圆面积用字母可以表示为 s 圆环等于 s, 外圆减 s 内圆。 如果用大写字母二来表示外圆的半径,用小写字母二来表示内圆的半径。 圆环的面积也可以写作派乘大二的平方减派乘小二的平方。根据乘法分配率,我们也可以将相同的因数派提取出来,写作派乘大二的平方减小二的平方的差。 在这样两种计算圆环面积的方法中,通过观察可以知道,只要已知外圆半径和内圆半径,我们就可以求圆环的面积了。在实际计算时,利用下面这个方法能够使计算更为简便。 接下来我们利用刚刚总结的圆环面积的计算方法来试着计算下面圆环的面积,请同学们先自己来试一试吧! 根据 s, 圆环等于派乘大二的平方减小二的平方的差可以列式,三点一四乘十二的平方减八的平方的差。 计算时同样是要先算括号中的平方运算,因此,等于三点一四乘一百四十四减六十四的差,就等于三点一四乘八十等于二百五十一点二平方厘米。完成答话,同学们,你们算对了吗? 再来看一个实际问题,一个圆形环岛的直径是五十米,中间是一个直径为十米的圆形花坛,其他地方是草坪。草坪的占地面积是多少?如图所示。我们可以知道,代表草坪的绿色 部分其实就是一个圆环,因此,求草坪的占地面积就是求圆环的面积。由于题目中已知的是外圆和内圆的直径,因此我们要先分别求出外圆和内圆的半径, 再利用三点一四乘二十五的平方减五的平方的差来求圆环的面积,完成计算等于一千八百八十四平方米。最后完成答话。 再来看一个问题,一个圆形喷水池的直径是八米,在他的周围铺一条一米宽的小路,这条小路的面积是多少?同学们,你能根据题目中的描述画出示意图吗? 根据提议,有一个圆形喷水池,它的直径是八米,在他的周围有一条一米宽的小路,因此要求的小路的面积其实就是一个圆环的面积。 根据已知喷水池的直径是八米,就可以求出他的半径是四米,如图所示,也就是这个圆环的内圆半径是四米。 如果想要求这个圆环的面积,我们还需要知道什么信息呢?对了,还需要知道外圆的半径。 在图中我们可以直观的看到,外圆的半径其实就等于内圆的半径加上环宽,因此外圆的半径就是五米。接下来根据三点一四乘五的 平方减四的平方的差,就可以求圆环的面积了。完成计算,圆环的面积是二十八点二六平方米,也就是这条小路的面积是二十八点二六平方米。 接下来我们再来看这样一个问题,左图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。 如图所示,阴影部分并不是一个圆环,该怎样求他的面积呢?与我们研究圆环面积的方法相类似, 我们还是可以先求出大圆的面积,再从中减掉小圆的面积,剩余的就是阴影部分的面积了。根据已知,大圆的半径是六厘米,小圆的直径也是六厘米,所 先利用六除以二求出小圆的半径是三厘米,利用三点一四乘六的平方求大圆面积,再利用三点一四乘三的平方求小圆面积,二者求差就是阴影部分的面积了。 完成计算,最后等于八十四点七八平方厘米,这就是阴影部分的面积。 在解决完这个问题之后,我们回过头来再观察这个算式,同学们对比一下圆环面积的计算方法,你有什么发现吗? 是的,它其实就是派乘大二的平方减派乘小二的平方。根据我们所学的圆环面积的计算方法,它还可以表示成派乘大二的平方减 小二的平方的差。因此,除了这种方法以外,我们也可以直接利用三点一四乘六的平方减三的平方的差来求阴影部分的面积,完成计算,同样是八十四点七八平方厘米。 从这个问题中我们发现,虽然这幅图中的阴影部分不是圆环,但是求阴影部分面积的方法和求圆环面积的方法是一样的。 其实像这样的从大圆中挖去一个小圆求剩余部分面积的问题,无论这个小圆在什么位置上,都可以利用大圆面积减小圆面积求剩余部分的面积,因此他的计算方法和圆环面 级的计算方法是相同的。再来看这样一个求半圆环的周长和面积的问题,我们先来看一看它的周长, 同样的可以先描一描他的周长,在描的过程中感受一下他的周长由哪几部分构成。如图所示,这个半圆环的周长包括外圆周长的一半和内圆周长的一半,还有两个环宽。 在计算它的周长时,我们可以利用外圆直径减内圆直径,先求两个环宽的长度和 再利用圆周长的计算方法列式,三点一四乘十二乘二分之一求外圆周长的一半, 再加上三点一四乘八乘二分之一求内圆周长的一半,最后加上刚刚求出的两个环宽的长度,就是整个半圆环的周长了。完成计算最后等于三十五点四厘米。 再来看它的面积,这个半圆环的面积其实就是圆环面积的一半。 由于题目中已知的是外圆和内圆的直径,所以我们要分别求出外圆和内圆的半径, 再利用三点一四乘六的平方减四的平方的差,求圆环的面积,再乘二分之一就是半圆环的面积了。完成计算,这个半圆环的面积是三十一点四平方厘米。最后完成答画。最后 我们来看这道题。土楼是福建、广东等地区的一种建筑形式,被列入世界物质文化名录。土楼的外围形状有圆形、方形、椭圆形等。 有两座地面是圆环形的土楼,其中一座外直径是三十四米,内直径是十四米,另外一座外直径是二十六米,内直径也是十四米。两座土楼的房屋占地面积相差多少? 在了解了有关土楼的知识之后,我们来提炼一下题目中的已知信息和问题。 首先这两座土楼都是圆环形的,并提供了这两个圆环的相关数据。而要求的问题,两座土楼的房屋占地面积相差 差多少,其实就是求这两个圆环的面积相差多少。我们可以用图示来表示题目中提到的相关数据,要求的就是这样,两个圆环的面积相差多少。同学们自己先来试一试解决这个问题吧。 我们来分享两种解决这个问题的方法。第一种方法,既然要求这两个圆环面积相差多少,我们就可以先分别求出两个圆环的面积。 先来看左边这个较大的圆环,根据外圆直径是三十四米,求出外圆半径是十七米,根据内圆直径是十四米,求出内圆半径是七米。再利用 三点一四乘十七的平方减七的平方的差,就可以求出该圆环的面积了。最后等于七百五十三点六平方米。再来看第二个圆环,同样的,根据外圆直径是二十六米求出它的半径是十三米, 他的内圆直径也是十四米,所以半径也是七米。这在前边已经求过了,这里不重复列算式了。接下来利用三点一四乘十三的平方减七的平方的叉,求出这个圆环的面积是三百七十六点八平方米。 最后利用七百五十三点六减三百七十六点八,就可以求出这两个圆环的面积相差三百七十六点八平方米。完成答话。 这种方法普遍适合于求任何两个圆环面积相差多少的问题,而针对这道题,其实还有另外一种方法,这和他们的形状特征密切相关。同学们再来观察这两个圆环,他们有什么相同的地方吗? 相信同学们已经发现了,这两个圆环的内圆大小是完全相同的, 如果我们把这两个圆环重合到一起,他们的内圆可以完全重合,而外圆的大小是有所不同的。 因此,要求这两个圆环的面积差,其实就是求红色部分的圆环的面积。在这个圆环中,外圆直径是三十四米,他的半径就是十七米。内 圆直径是二十六米,他的半径是十三米。所以红色部分圆环的面积可以列式为三点一四乘十七的平方减十三的平方的差。完成计算, 这个红色圆环的面积就是三百七十六点八平方米,和方法一的结果是相同的。 最后我们对本节课的学习进行一下回顾与反思。首先我们认识了什么是圆环,两个半径不相等的同心圆之间的部分就是圆环, 在此基础上,我们学习了圆环面积的计算方法。圆环的面积等于外圆面积减内圆面积,根据圆面积的计算方法,可以表示为派乘大二的平方减派, 派乘小二的平方还可以根据乘法分配率将派提取出来。这就是我们本节课要学习的所有知识了,请同学们根据这节课的学习完成以下自我挑战, 这节课的学习就到这里,同学们再见!
510名师课堂 01:02
01:02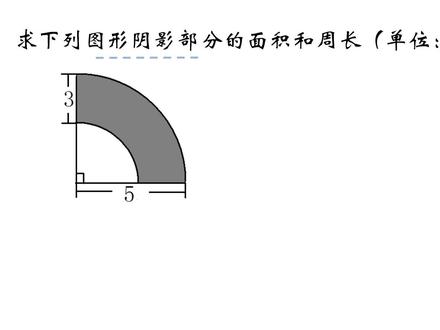 10:42查看AI文稿AI文稿
10:42查看AI文稿AI文稿小朋友们好,欢迎来到杨老师课堂,这节课我们一起学习。求阴影部分的面积,下面看题,求下列图形阴影部分的面积和周长单位等于零。 首先我们看给出的这个图是一个上环,现在要求阴影部分的面积就是求这个上环的面积。这里给出大扇形的半径为五厘米,上环宽度为 三厘米,那这里要求阴影部分的面积。我们可以先看给出的这个角是 圆心角为九十度,圆心角为九十度,说明这个九十度占整个圆周角的四分之一,那这个 扇形它的面积就是整个圆面积的四分之一,同样这个扇环的面积, 也就是阴影部分的面积是整个延缓面积的四分之一。那现在我们只要把延缓的面积求出来,再乘以四分之一,就是这个阴影部分,也就是上环的面积啊。下面我们看做法,这里写面积, 好大亮点,这里求的是面积,首先看答案,在这里已经知道,等于 五厘米,小二就等于大二,五减去三。等于 二厘米,好,延缓的面积公式是 s 缓等于 pat 到二的平方, 减去小二的平方,等于。这里三点一四乘以大二,在这里是五就五的平方减去小二,这里是二二的平方。等于三点一四乘以 五,五二十五减去二二得四。等于三点一,四乘以二十五减四,二十一。 好,下面我们计算一下,这三点一四乘以二十一,一四得四,一一得一,一三得三。 下面二四得八,一二得二,二三得六,好,四,搬下来,一加八,九,三加二五六。这里两位小数乘对得起,重用向左数两位,结果就是六十五点九四, 好,写下六十五点九四,单位是平方厘米。好,在这里算出来是这个上环的面积。啊,这里他是阴影部分啊,那就是也就是要求整个上环的四分之一, 所以 s 上画啊,就等于四分之一乘以这里派二方 就是这个上延,这个上环的上环的面积,四分之一乘以这里延缓是六十五点九四,乘以六十五点九四。好,我们等一下,六十五点九四, 除以这里的四啊上一一四得四六减四得一五,扳下十五三四,这里十二 三,好,小数点放下去,这个九翻下来四九三十六,好,九减六,等于三 四搬下来,四八三十二,好,来二十四五二十,结果就是剩的 十三点九八五单位,这个是平方厘米,这里是 s 上环的面积,也就是这个 s 阴影部分的面积,所以这里也可以写成 s 阴,就是阴影部分的面积。 好,这里我们求出来是这个上环的阴影部分的面积。好, 我们把这个打的草稿,把它啊涂掉啊涂一下,那这里散出来他的阴影部分的面积。下面我们要散他周长的面积, 那我们观察这个土给出的这个土呢?在这里他这里是 同样这个上环是整个延缓面积的四分之一,那在这里他阴影部分的这个周长,同样也注意是外面 就是整个这个延缓的,这里是四分之一,但这里要注意他的周长是外面这一条 长度,还有里面这个小延缓,这个弧长就大延缓,这档弧长 加小,加这个小圆,这个弧长再加两端,两端都是三厘米,加两个三厘米,三者就是整个这个阴影部分的周长啊,下面我们做一下,把周长我们写在这边右手边, 这里写周场啊,大两点。第一步外面这个胡场是大胡场,大胡场是整个大眼周 州厂的一半,因为盐的粥厂,我们是二拍二。好,那这里就大盐这个粥厂就是二拍 是 c, 大等于二,派就大,二等于二乘以派三点一四乘以,这里二就是五,就等于二五一十加三点一,四是三十一点四,单位是厘米。 这个是大型的周长啊,他这里呢要去他的弧长,他对应的年轻就要九十度,那他的弧长就是整个眼周长的四分之一,所以这里是 啊 c 这个弧长就等于三十一点四乘以四分之一。 好,我们看一下,三十一点四除以四十四八大了。好,我们这里算一下,三十一点四 除以四四七就得二十八。好,十三十一减八得三三十四,四八,三十二五是七点八五,七点八五,单位是雷鸣。 好,这个是这个大湖州场下面小湖州场啊,我们直接上了小湖, 这个小幅周长就是小圆,周长四分之一,直接代工是四分之一乘以二,乘以派派三点一,四 乘以小二,小二。在这里我们记住是这一段,这一段长度,这段长度呢,在这里是五减三,就等于二厘米,所以这里是乘以二就等于四分之一 乘以二,乘以三点一四,再乘以二,最后就等于三点一四, 单位是厘米啊,这里观察二乘二点四,四和分母四也分一,一乘三点一四就三点一四厘米。现在要求他整个周长,整个周长是大幅的周长七点八五米厘米, 加上小幅的长度,三点一四,再加两个啊,这个宽度就是这里宽度这档宽度三厘米,还有这档宽度三厘米啊,那整个这个阴影部分的周长就是 c 阴阴影部分的周长就等于 好,这是大幅的出场,加上小幅的长度,加上这里的三乘以二,就等于大幅的长度,这里,这里是 七点啊,八五加小幅的长度,这里三点一四, 再加这里的二三得六,好,我们把它算出来,七点八五,加上三点一, 加一下五加四,九八加一,九三加七 十,就十点九九,再加六就是十六点九九,单位是雷鸣啊,这形象好,那是这个题,那这个题呢,我们做的时候一定要注意, 第一个一定要找准他周长是封闭图形一周的长度,所以散的时候是外面的长度,千万不要把里面的长度散在里面,所以散的时候 外面的就是周长。那做题的时候方法很灵活,我们不是只有唯一的做法,可能有很多种做法,所以在这里同学们在做的时候一定要一定要注意 啊,千万不要啊做错啊。那小朋友们这节课呢?今天我们就学习到这里,如果有不懂的做法,欢迎大家在评论区留言,下一节课我们继续来讲,小朋友们再见。
754杨老师趣味数学 07:07查看AI文稿AI文稿
07:07查看AI文稿AI文稿hi, 同学们大家好,欢迎来到卡老师的数学小课堂,我是最懂你们的卡老师,今天啊,我们要一起学习的是同步小学数学六年级上册第五单元的第六课时,叫做扇形。那什么是扇形呢?我们通过几种生活当中常见的事物来了解一下。 好,我们来看这里面呢,分别是扇贝、扇形走和折扇的图片。好,我们可以看到啊,这几种事物的形状呢,本身就比较接近,有共同点,同时呢,他们的名字里面都有一个扇字, 现在啊,我把这几个事物呢抽象成几何图形,哎,画出来就得到了我们扇形的形状。那课本上呢,对于扇形是这样定义的,一条弧和经过这条弧两端的 两条半径所围成的图形叫做扇形。哎,这句话看起来很长很绕口,是不是?好,那老师,简单来说,其实啊,这句话就是在告诉我们,一个扇形啊,是由三条边组成的,哪三条边呢?首先呢,是两条半径, 接下来呢,还有一条弧,哎,这三条边中间围成的部分就是我们所谓的扇形了, 这样来看的话呢,其实扇形啊,它就是一个圆的一部分,那这个弧对应的又是什么呢?这个弧其实就是圆周长上的一段,对吧? 好,那关于扇形呢,老师再补充一个概念,什么概念?我们说扇形,这里面有一个角,哎,同学们有没有注意到这个角呢,有个名字叫做圆心角, 什么意思呢?顾名思义,哎,你可以从字面意思去理解,就相当于是顶点在圆心处的角叫做圆心角,它的两条边呢,分别对应的是两条半径。好,那和它类似的呢,还有一个角,老师来画一下。 好,这个角呢,在这里,这个角呢,也有个名字叫做圆周角。 好,相比较而言的话呢,组成角的两条边就不再是半径了,对吧?好,在这里面呢,圆心角和圆周角呀,本身是我们初中才会接触到的概念,详细阶段呀,你只需要能够判 端出来。哎,这两者不同就可以了。这个是在我们的课后练习题里面比较常见的题型好,其他的性质呢,咱们不再多做补充。好的,说完了善行的特征,那接下来呢,咱们来看一下下面的课后练习题。 首先第一题,像下面这样一个圆环被截得的部分叫做扇环,求出下面扇环的面积分别是多少。 好,我们来看一下,他既然提到圆环了,那我们不妨呀,先把这个图形给他补充完整,先画出来一个圆环的形状。好,那我们可以看一下,补充完之后呢,应该是这个样子。 哎,这样就很明显了,这个上环就是他说的是圆环的一部分,对吗?至于和圆环之间有什么样的关系,从这个 图里面我们能看出来,这个上环呀,其实恰好就是这个圆环的四分之一。好,那上来呢,我们的速度就有了,先求圆环,然后乘以四分之一就得到上环了。那圆环的计算呢?我们上一节课刚刚讲过圆环的面积公式,直接套公式是不是就可以了?好,那我们来看一下公式, 三点一四,乘以大儿的平方减去小儿的平方。好,大儿在哪呢?在这里,也就是五分米, 小儿呢,哎,小儿在这里,但是这一段我们是不是不知道呀?没关系,我们知道这一段是两分米,那我们用整个大圆的半径减去这两分米,得到的是不是就是小圆的半径了? 好,所以前面我们再加上一步五减二等于三分米。好,所以下面直接减去三 的平方,计算出来的结果呢,等于五十点二四单位平方分米。好,整个这个圆环的面积我们就有了, 那接下来呢,我们说了,他占整个圆环的四分之一,那我只需要用五十点二四乘以四分之一,当然这个地方除以四也是一样的。好,求出来最后的结果等于十二点五六平方分米。 那这道题呢,到这我们就做完了,最后答 好,那第一题呢,我们就完成了,接下来呢,我们再来看第二个图,哎,你会发现啊,第二个图其实就相当于是第一个图怎么样? 复制粘贴了一下对吗?好,第一个图里面呢是一块,第二个图里面呢是两块,所以呢,他的求解思路也很简单,直接求出来其中一块,然后呢,乘以二,是不是得到的就是整个涂色部分的面积了。好,当然呢,通过观察我们也可以发现, 这里面啊,这两部分扇环其实是一模一样的,所以呢,一个扇环占整个圆环的四分之一,那两个合起来呢,其实就是二分之一了,也就是整个圆环的一半了。那上来呢,我们还是把整个图形补充完整 好,老师画的比较简单,那这里面呢,我们就能看出来了,依然是一个圆环, 我们还是按照上一道题的思路,先求整个圆环部分的面积好,还是三点一四 乘以大儿的平方减去小儿的平方,在这里面呢,大儿是四分米,小儿呢依然不知道,需要我们计算一下。好,那这一段呢,我们可以看出来,相当于是大圆的半径,减去上面的一分米。好,所以四减一等于三。 好,下面减去三的平方就可以了,求出来的结果呢,等于二十一点九八平方分米, 到这呢,整个圆环的面积我们就求出来了。最后求扇环,我们刚才说了,两个扇环啊,可以合二为一,变成圆环的一半,所以呢,二十 一点九八乘以二分之一或者除以二都可以,等于十点九九平方分米。好,最后答案 好,那到这呢,这个扇环的面积我们也就求出来了。好,所以呢,整个扇形,今天呢,所有的题目我们就全部讲完了,那同学们,我们下一节课再见吧。
91秒懂语文 03:07查看AI文稿AI文稿
03:07查看AI文稿AI文稿咱们看一道六年级的题,像这样一个圆环被结得的部分叫做单环,你能求出这个单环的面积吗?我们知道,圆环的面积 就是大圆的面积减去小圆的面积,那善缓的面积等于什么呢?善缓的面积就应该是大善的面积减去小善的面积。善行是圆的一部分, 究竟是多大部分呢?这取决于圆心角的度数。我们看这个扇形,它的圆心角是个直角,就是九十度,那这个扇形就是个九十度的扇形,它的面积就是圆的面积的 四分之一。所以呢,这道题有一个做法,就是用四分之一大圆的面积 减去四分之一小圆的面积,也就是大扇的面积减去小扇的面积。我们先写下来,四分之一大圆的面积就是大扇形的面积,四分之一小圆的面积就是小扇形的面积, 他们相见就得到了善缓的面积。当然,这道题还有另外一种做法,既然善行是圆形的一部分, 那善环就是圆环的一部分,而圆环我们是会求的,那这个善环的面积是圆环的面积的几分之几呢?毫无疑问,应该是圆环面积的四分之一,所以 善环的面积等于四分之一圆环的面积,那圆环的面积我们已经会求了。咱们算一下,等于四分之一乘圆环的面积,等于派 乘大 r 的平方减去小 r 的平方的叉。接着算,等于四分之一乘三点一四 成。咱们看大儿就是大圆的半径,这是七分米, 那就是七的平方减去小儿,小儿是这一部分,大儿是七分米,这个环形的部分是三分米,那七分米减去三分米, 小儿这部分就是四分米,那就减去四的平方,接着算,等于四分之一乘三点一,四 乘七七四十九四四十六,四十九减十六等于三十三,咱们自己算一下,最后结果应该是二十五点 九零五。答,该善还的面积是二十五点九零五平方分米,这里也要写上单位平方分米,你学会了吗?
36家长学堂 徐老诗
猜你喜欢
- 1.6万老三的梦想












