对数函数的图像和性质 乐乐课堂
粉丝5320获赞2.7万
相关视频
 03:18
03:18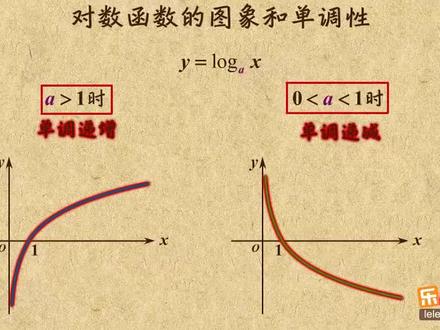 02:09查看AI文稿AI文稿
02:09查看AI文稿AI文稿这个视频我来讲讲对数函数的图像和单调性。前面我已经讲过,对数函数 y 等于 log ax, 当 a 大于一时,图像单调递增大致是这样子的。 当 a 大于零小于一时,图像则是单调。季节大致是这样的。所以不管是要判断对数函数的单调性,还是要画出他的图像,关键都是看底数在哪个范围。 知道了这一点,我就要来考考你了。如果告诉你 a 大于零,那函数 y 等于 log, a 加一 x 是增函数还是减函数,你能大致画出他的图像吗?要求他的单调性和图像,当然得找出底数的范围啦。 a 大于零,所以 a 加一大于一,那函数就是增函数,画出图像来大致就是这样的。刚才的问题中, a 的范围直接告诉你了,但有时候 a 的范围会给的很寒 去。比如告诉你直线 y 等于 a, x 加 b 的图像是这样的。那图像 fx 等于 log a b x 是增函数还是减函数?图像又是咋样的呢? 先观察一次函数的图像, a 是图像的斜率,那斜率是几呢?你可以画一条倾斜角为四十五度的直线来比一比,这条直线的斜率为一,那 a 就比一小,显然 a 又是大于零的,所以 a 大于零小于一。 再看 b, 他是图像和外轴的拮据,所以 b 也大于零小于一,那 a 和 b 乘起来也就大于零小于一。所以这个函数是减函数,画出图像来大致是这样的。 刚才都是通过底数范围来求单调性和图像。反过来,通过图像或者单调性,你也得能找出底数范围。比如告诉你 y 等于 log, a 加一 x 是减 函数,你能求出 a 的范围吗?现在是减函数,那对应的底数应该大于零小于一,所以 a 大于负,一小于零。 好了,以上就是这个视频的全部内容。关键记住一点,对于对数函数, y 等于 log a x, a 大于一十是增函数,图像大致是这样的 a 大于零小于一十是减函数,图像大致是这样的怎么样,听明白了吗?如果明白了,就赶紧去刷题吧。
 04:06
04:06
猜你喜欢
- 1219小敏@
最新视频
- 1.1万我是周周














![对数和对数函数[高三一轮复习8] #高中数学 #高考数学 #对数函数 #函数 #对数运算](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/3a5716457920eca6a2d5770e9560d2a0~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2080396800&x-signature=St%2FtrEh4h%2FclP7GZF4LkfoVTfrs%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251207003024A80A71F8B3DBC95C640F)
