对称轴怎么做,八年级上
同学们大家好,欢迎大家来到小孙数学,本节课我们开始学习第十三章轴对称。 同学们,我们生活在一个充满对称的世界中,许多建筑物都设计成对称型, 艺术作品的创作呢,也往往从对称的角度考虑,自然界的许多动植物也是按对称型生长, 在中国的汉字中,有些也具有对称性,对称给我们带来美的感受,给人以平衡与和谐的美感。从本节课开始呢,我们一起来学习轴对称。 在我们的生活中啊,对称现象无处不在,比如黑板、桌椅,我们的身、 身体、飞机、汽车等等,很多很多都是对称的。好了,那既然我们给出了这么多的例子,下面我们就来一起研究什么是轴对称图形。准备几张纸,把每一张纸对折, 剪出图案,再打开就剪出了一张张美丽的春花。你能发现这些图案有什么共同的特点吗? 对,这些窗花可以沿折痕对折,折痕两旁的部分能完全重合。 不仅窗花可以沿一条直线对折,使直线两旁重合。我们将这些图形沿着 一条直线折叠,直线两旁的部分能够完全重合,那我们就把这样的图形叫做轴对称图形 好了。我们给出轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形, 这条直线叫做对称轴。这时呢,我们也可以说这个图形。关于这条直线成轴对称, 大家看这些图形,他们沿某一条直线折叠,直线两旁的部分呢,能够互相重合,那这些图形啊, 就是轴对称图形,这条直线呢,就是他的对称轴,这时我们也可以说这个图形关于这条直线成轴对称。 大家在想,一个轴对称图形的对称轴,一定是一条吗?不一定,有些轴对称图形的对称轴啊,只有一条,比如第一个图形,有的轴对称图形的对称轴呢,有很多条,甚至无数条, 比如这第二个图形,他有五条对称轴,这第三个圆呢,他有无数条对称轴。 所以呢,轴对称图形的对称轴啊,不一定只有一条。下面大家再看这两组图形, 你发现了什么?有的同学说啊,刚才所学的轴对称图形是指一个图形, 而这些图形呢,每组都是两个图形,那能不能说这两个图形关于这条直线成轴对称呢? 嗯,同学们的观察能力都很强。这两组图形和刚才我们讲过的图形有所区别,每一组都有两个图形,如果把每一组图形沿着虚线折叠, 左边的图形和右边的图形会完全重合,那么我们就说这两个图形,关于这条直线成轴对称。下面我们给出定义,把一个图形沿着 某一条直线折叠,如果他能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称, 这条直线叫做对称轴,折叠后重合的点是对应点, 叫做对称点。比如这两个图形关于这条直线乘轴对称点, a 的对称点就是点 a 撇点 b 的对称点是点 b 撇点 c 的对称点是点 c。 撇。好了,下面大家思考乘轴对称的两个图形全等吗? 是全等的,因为这两个图形啊,可以完全重合。好,这是乘轴对称的两个图形,是全等的,大家再 思考,对于一个轴对称图形,就这一个图形来说,我们沿着对称轴分成两个图形,那么左右这两个图形全等吗? 也是全等的,因为左右这两个图形啊,是关于这条直线成轴对称的,他俩是能够完全重合的。 好了,那很多同学呀,一开始学习的时候呢,对于轴对称图形以及成轴对称的两个图形,这两个概念呢,容易混淆,我们来看一下 轴对称图形,它是一个具有特殊形状的图形,它是一个图形。 而乘轴对称的两个图形呢,它是指图形的位置关系,这两个概念呢, 不要混向,这是他们的区别,那二者呢,也有一定的联系,轴对称图形和成轴对称的两个图形都有一条直线,就是这条虚线, 沿这条直线折叠,可以完全重合。我们再看,那如果我们把轴对称图形沿着对称轴分为两部分,那么左右这两个图形就是关于这条直线成轴对称。 反过来,如果把成轴对称的两个图形看成一个整体,也就是我把它呀看成一个图形, 那么他就是一个轴对称图形。好了,那以上呢,就是本节课的全部内容,下面我们回顾 一下本节课头学习了什么。首先呢,我们在生活的实力中认识了什么是轴对称图形,并且会找出他的对称轴。 然后我们学习了两个图形,关于某条直线乘轴对称。最后呢,我们学习了轴对称图形与乘轴对称的两个图形,他们的区别和联系。好了,本节课就到这里,同学们,我们下节课见。
粉丝9.5万获赞29.2万
相关视频
 01:22查看AI文稿AI文稿
01:22查看AI文稿AI文稿话说狗蛋的姑姑是空姐,经常会从某某国带小礼品给狗蛋,这回啊,他从英国带来了人家的传统节日糕点姜饼小人。姑姑到狗蛋家的时候,刚好狗蛋和王小锤在写作业。狗蛋想,朋友嘛,不仅有难同当,还要有福同享嘛, 就跟小锤说,哎,我掰给你一半吧。小锤心想,狗蛋掰的肯定有大有小,自己肯定拿小块,就眼珠一转,说,咦,这不是个轴对称图形吗?你拿刀沿着对称轴切,不就能保证两半一样大了吗?狗蛋说,对呀, 可拿出了小兜,他才记起来,自己的脑子里只有一种找对称轴的方法,就是把纸对折,重合后找折痕那种。可饼干是脆的,没法折呀。 那对称轴要怎么找呢?他扭头一瞧,看见王小锤的嘴角浮现出了阴森森的笑容,不知从哪里套起了咫尺和圆规。 狗蛋感到脊背发凉,正要开口,忽然听到桌子上一声叹息,哎,难道你忘了周对称的性质吗?狗蛋不敢相信自己的耳朵,这话难道是姜饼小人说的?狗蛋只觉得头咚的一下子便眼前一黑,失去了知觉。
49洋葱学园学习库 03:23查看AI文稿AI文稿
03:23查看AI文稿AI文稿设计轴对称图案轴对称图形均衡和谐,给人与美的享受。 人们常常利用轴对称设计图案,在日常生活和建筑设计中也常用到。 设计轴对称图案的关键在于轴对称变换,请按暂停键分别做下列图形。关于虚线的对称图形, 为了方便,期间常常用正方形、三角形、菱形等网格纸, 比如我们该图利用菱形网格纸画出了盆花的图案。设计轴对称图案的关键在于对称轴。请你画出下列图形的对称轴 共有四条,有一些彩色图案,不仅是轴对称图形,而且颜色也对称。如果考虑颜色的对称,请问图一和图二中各有几条对称轴?图一 两条对称轴,图二只有一条。如果把图一中左上方和右下方的小方格也涂上红色,请问他有几条对称轴?在原有的 两条基础上又增加了两条,所以共有四条对称轴。那改变图案中哪些小方格的颜色就能使它也有四条对称轴,请按暂停键试一试。 用这四张纸片拼合,能得到不同的图案。比如 上面三个图案各有几条对称轴, 你还能拼出其他图案吗?请按暂停键试一试,并指出你所拼得的图案有几条对称轴, 分别有两条对称轴,一条对称轴没有, 因为最后一个图案不是轴对称图形。日常生活中,花边艺术大量用到了轴对称设计 都是用到了轴对称,变幻、美轮美奂的剪纸艺术更是把轴对称设计发挥到极致。请你观察这些作品的制作, 你能得到庆丰灯笼的剪纸作品吗?试试看!
23以微课堂 22:29查看AI文稿AI文稿
22:29查看AI文稿AI文稿今天我们学习设计轴对审图案。轴对审图形均衡和谐,个人与美的享受。 这一件乾隆时期的作品,拍了两个多亿人民币。屏上的文样是轴对称图形,构图非常精巧。 这是一枚唐代的花钱,他的中间是正五边形, 外面是梅花的形状。清代的, 因为花钱,大家可以看到它是一个周对称图形。古代的装饰纹样, 大家熟悉的中国结剪纸,中间经常会有轴对称的这种图形。 轴对称图形在生活中运用非常广泛,大家很熟悉的微信的,微信的表情。 交通标志,银行的标志。这里面我们可以看到 银行的标志。我们这里面三个标志,他的都是古代的钱的形状,外圆内方,体现古人的天圆地方的思想。他的区别是中国银行中间是个中字。 农业银行,这里面加了一个麦穗。 工商银行啊,中间是工商的工资。 这里面分别是国家免检标志、中国环境标志、绿色食品标志。 免检标志是圆形,正中是免字,汉 与拼音。他的重道连接,图形上时下虚。他指的是明年产品的外在及内在质量都符合有关质量法规的要求。 中国环境标志由中心的青山、绿水、太阳及周围的十个环组成。图形的中心表示人类赖以生存的环境, 外围的十个环紧密结合,环环相扣,表示公众参与,共同保护环境。 绿色食品标志上方为太阳,下方为叶片, 中心为对雷,描绘了一副明媚阳光照耀下的和谐生机, 表示绿色食品是出自优良生态环境的安全无污染食品。 从这里面我们可以看到我们进行一些设计的时候啊,都是有丰富的内涵。那么你想设计轴对称图案吗?我们如何来进行设计轴对称图案呢?先看一个操作, 我们在一张纸上滴上一滴墨水,将这张纸对折,然后打开,我们发现 这里面两个色块形成一个着对称。 当我们改变这条对称轴的位置,那么两个色块所形成的图案很明显是发生的变化。 那我们在这里面我们可以发现我们一个基本元素,一个基本元素。通过改变对审中的位置,我们可以形成一个 不一样效果的一个图案。所以说设计着对审图案的关键是确定对审轴。 我们先看一道题目,如图, 点 a、 b、 c 都在方格指的割点上。请你再找一个割点 d, 使点 a、 b、 c、 d 组成一个轴推式图形。 这片片我们怎么来进行找,比较方便一些。我们可以利用对称轴。 首先我们以直线 bc 左右对称揉, 我们可以找到 a 点。关于 b 四的对称点,第一个点 d, 我们也可以以 bc 线段 bc 的垂直平分线左右对称揉。那这样点哎。关于这条直线 线的对称点啊,就在这样的位置。同样我们以直线 ab 作为对称中点 c, 关于直线 ab 的对称点就在下方。 我们也可以以线段 ab 的垂直平分线左右对称中,这样点 c 的对称点就在这条对称中的左侧 啊。从分类的角度,我们也可以考虑直线 ac。 还有线段 ic 的垂直平分线左右对称中。 如果以直线 ic 左右对称中,那么点 b。 关于 实现 ic 的对称点不能落在割点上,这个对称点是存在的,但是呢,不是在割点上。而我们要求的是再找到一个割点地, 同样以线段 ac 的垂直屏分线作为对称轴的话,点 b 也不能够落在个点上。所以这里面隔点 d 一共有四个答案。 那我们这道题我们在进行解决的时候,首先我们就是研究对称轴,通过对称轴的分类找到了对称点。 下面我们看正方形,他有四条对称。 下面我们就来进行一组练习,利用正方形的对准轴来进行研究。问题 一右图各有几条对称中,在这里面我们要考虑色块。 我们沿着这样的一条对角线所在的直线翻折,直线两旁的部分是可以重合的。 我们再沿着这样一条对角线所在的直线翻折,直线两旁的部分也是可以重合的 啊。我们正方形有四条对角,这四有四条对称轴。那如果我们过水平的线或者竖直 的线可不可以呢?线还是不可以的。再看第二幅图, 我们以这条对角线所在的直线为对称中,发现两侧是对称的。 那么其余的大家可以看一下子。我们以这条对称轴对角线所在的直线作为对称轴是不可以的。 以水平线作为对称轴也是不可以的。以数值线为对称轴,所有两面也不对称啊。这样只有一条对称轴。 我们在此基础上改变上图中部分小方格的颜色,使他有四条对称轴,最少需要改变几块。 我们现在已经有两条对称中,那我们现在要想变成四条对称中。我们知道这个正方形整体一共是四条, 我们现在加上,我们再加上一条,这样我们要改变 这一个色块对应的一个。同时右上角的色块所对应的右下角的这两块要涂上颜色。 这个时候我们在这验证,我们过上下对边的终点的直线,所有对称轴的话,整个图形也是一个轴对称,这样我们 需要改变两块颜色。再来看一下第二幅图,这幅图已经有一条对称轴, 如果我们再加一条对称轴,那我们现在发现上面的这一块所对应的下面这一块需要涂上颜色。 我们再来增加一条。对称中,我们发现右面的一个色块对应的左边需要涂上颜色。 最后我们来验证一下这条对角线所在的直线所有对称中整个图形也是一 一个成轴对称,这样我们也需要涂两个色块。 第二道题比第一道题要复杂一些吧。好,下列方格中各画出一个各点三角形,使所画的三角形与圆三角形从轴对称。 那我们利用正方形有四条对称轴,我们先把四条对称轴画出来, 那么以这四条对称轴,我们可以画出来他的轴对称的三角形。 这样有四个答案。那么还有没有其他答案呢?我们一个一个来进行分析。第一幅图,如果把对准揉左右平移, 发现这个三角形会到正方形的外面, 如果把这身柔旋转啊,这个三角形的三个顶点啊,也不会落在割点上。 第二幅图。嗯,把这条对称中上下拼一啊,发现这个三角形啊,也是啊, 出了正方形,如果把它旋转一样道理,这个三个定点也不能落在这一个 隔两。第三幅图和第二幅图的情况类似,那我们再看第四幅图,我们发现 这条对称轴向上平移,这个三角形啊是出去了,但是如果向下来,这个三角形跟着是向下平移, 哎,那我们就会出现第五种情况。当这是揉平移到下面小正方形的这一个左右两边这边中点的时候, 那么小钟这个三角形再次落在个点上。那这道题很显然就是在刚才 四条顿时的基础上,我们又探索出来一种情况。 下面我们来看如何来进行拼图,并四张基本图案。拼出的图案是轴对称图形吗?如果是有几条对称轴, 第一个我们沿着水平线分着上下可以重合。第二个过上下两边终点的直线分着左右可以重合。 第二幅图啊,这个我们找不到他的对称中第三幅图我们可以做一条水平线, 上下两边重点的直线是不可以的。 接着我们来进行 这是一道这道题是给拼好,让你来进行判断。下面呢,我们给四张贴纸, 让你把它贴在方格中,使整个图案成为一个轴对称图案。 我们怎么样来进行拼?我们来看一下。这四个贴纸都是一样的,而每一张贴纸本身他是一个轴对称图形, 只有一条对称轴,只有一条对称轴水平线,他不是对称轴数据线,不是对称轴 过对角线的焦点,而这个对角线所在的直线不是对称中只有一条对称中。 我们来看一下如何拼。 我们提供第一个方案,这个方案大家可以看到,我们把这一个小花其中在中间, 然后我们上下上一排的左右两个相乘一个轴对称, 下面一排左右两个也形成周对称。 左右两列上下形成周对称,上下形成周对称。那么他们拼在一起啊,就是有两条对称中, 但是在里面对角线所在的直线,他不是一个轴。对审图形啊,他不是对审轴。 那如果我也想把出现四条对称的话,应该怎么办呢?你可以看到,除了让左右对称,上下对称,那对角线上呢?也应该是对称。 对角线上的。我们可以看到对角线所在直线,我们分着啊,可以重合的,这样我们可以得到 四条最深重。同样道理啊,这种方案也可以是四条最深重。 当然还有其他的拼法,比如说这一种,把它拼出来,发现左右是对称的,左右对称,但上下不对称, 沿地角线,他是不是对称的,所以他只有一条对称的。 好。请大家看一下几何画板设计着对称图案。第一个图 啊,是古代的装饰的纹样,我们可以看到 我们把这个图做一个基本图案,这个基本图案 沿着他这一条直线翻折啊,得到第二个图,第二个图再沿着一条直线翻折,得到第三个,以此类推。我们也可以 把前两个图做一个整体,以这条直线做一个对称中,然后一二翻到三四,也可以 前三个做一个整体,做一个对称。之后我们得到后面的三个,也可以理解为 前面四个左右一个整体,然后在这上有条对称中 啊。这是一组比较复杂的这一个周顿人图案, 任意改变线的位置。 哎,可以看到跟我们的感受是各不相同,那在这里面 实际上我们是在是在原地和八种分的基础上设计出来的, 那每一部分,每一部分,实际上我们的设计的时候,美感实际上并不足,但是通过我们不断的重复啊,整齐的排列,那么根据对称性,那这样的话呢,产生一个韵律感,那就富有美感了。 再来看一组, 这里面三个实际上也是一个图形,我们来欣赏一下。 好,下面了。 这两幅图啊,都是一个周顿神图形,大家自己可以创作一下, 靠后练习。如图,在正方形网格中,有两个小正方形被涂色,在图中再涂一个小正方形, 使得整个被图塞的图案构成一个轴。对选图形。那么图法更有几种?那我们在这里面我们可以看到它本身有一条对称轴, 然后在对唇之后我们再涂三个啊。再涂色的话会有三种方案, 那如果我们把水平线做对顺轴,那在下面可以通上一个,把数字线做对顺轴, 左边可以涂上一个,那这条对角线上啊,这条对角线如果作为对角线的话,我们需要涂几个呢?我们需要涂两块,这种方案是不行的, 所以我们再涂一个。状况下的话,会有五种。 人民在剪纸的时候常常利用轴对称设计团,你能得到青红灯笼的剪纸作品吗? 试试看。我们在里面关键就是找出他的对称轴啊,把它进行折叠, 我们剪出他的一半,铲开之后就得到一个完整的动能的形象。谢谢观看。
96冬瓜爱学习 05:27
05:27 24:43查看AI文稿AI文稿
24:43查看AI文稿AI文稿同学们好,我是来自北京市第四中学的王亚婷老师。接下来我们要用两节课的时间来学习画九对称图形。在这部分内容中,我们将要学习 做已知图形关于给定对称轴的对称图形认识在平面直角坐标系中,图形的对称引起点坐标的变化特点,并运用他们解决一些问题。 在之前的课程中,我们学过两个图形呈轴对称的相关概念和性质,下面我们一起来复习一下。 把一个图 图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线呈轴对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点 限制。如果两个图形关于某条直线呈轴对称,那么这两个图形全等 对称轴是任何一对对应点所连线段的垂直平分线。如图,对应点 p p 撇所连线段被对称轴垂直平分。 如图,在一张半透明纸的左边部分画出一只左手印。 如何画出与左手印关于直线 l 对称的右手印对,将这个纸片折叠折叠之后描图就可以描出对应的右手印, 此时画出的右手印与左手印是全等的,右手印上的每一个点都是左手印上的某一个点。关于直线 l 的对称点 对称点所连线段 p p 撇被对称轴 l 垂直平分, 由一个平面图形可以得到它关于直线 l 对称的图形,这个过程我们叫做轴对称变换。 这个图形与原图形的形状大小完全相同,这个图形上的每一点都是原图形上某一点关于直线 l 的对称点, 连接任意一对对应点的线段被对称轴垂直平分,如图, p p 撇被对称轴垂直平分,对称轴垂直平分,线段 p p 撇。 我们可以通过折纸描图的方法做出轴对称图形,同样的,我们也可以采用夹眼踏印的方法。 那么如何用作图工具做出已知图形的轴对称图形呢?思考,如果有一个图形和一条直线,如何做出这个图形? 关于这条直线对称的图形呢?刚刚有同学在描右手印的过程中,事先描出了几个关键的点,然后进行连线, 这也是我们数学中常用的一种方法。先从最基础的情况入手,我们知道点是最基本的几何图形,因此我们可以先研究做一个点关于直线对称的图形,再研究线,最后再研究图形。 例题一,求做点 a 关于直线 l 的对称点, 由轴对称的性质之,对应点的连线 a a 撇被对称轴 l 垂直平分,因此,我们可以先过 点 a 画出直线 l 的垂线垂足尾 o, 在垂线上截取 o a 撇等于 o a, 那么此时直线 l 就是线段 a a 撇的垂直平分线,则点 a 撇就是点 a 关于直线 l 的对称点。 第二问,求做线段 a b 关于直线 l 的对称图形, 线段由它的两个端点确定,因此我们不妨先做出这两个端点关于直线 l 的对称点。如图,分别做出点 a、 b 关于 与直线 l 的对称点 a 撇 b 撇,连接 a 撇 b 撇,那么则线段 a 撇 b 撇即为所求。 我们发现线段 a b 关于直线 l 对称的图形还是线段?那么如何验证画出的图形与线段 a、 b 是关于直线 l 对称的呢? 我们可以用折纸的方法折叠一下,看是否能完全重合。当然,我们也可以在纸线段 a、 b 上任意取一点 p, 看点 p 关于直线 l 对称的点是否落在线段 a 撇、 b 撇上。 如果说点 p 关于直线 l 对称的点没有落在线段 a 撇、 b 撇上,那么此时 a 撇、 p 撇、 b 撇就不在同一条直线上, 则它不是一条线段,显然是不对的。所以,点 p 关于直线 l 的对称点一定会落在线段 a 撇、 b 撇上,因此,线段 a 撇、 b 撇就是线段 a、 b 关于直线 l 的对称图形。 第三问,求做三角形 a、 b、 c 关于直线 l 对称的图形。 同样的三角形 a、 b、 c 是由它的三个顶点确定的,因此,我们不妨先做出三 顶点的对称点,然后再连接。如图,分别做出点 a、 b、 c 关于直线 l 的对称点 a 撇、 b 撇、 c 撇, 连接 a 撇、 b 撇、 b 撇、 c 撇、 c 撇、 a 撇,则三角形 a 撇、 b 撇、 c 撇即为所求。因此,我们在做一些图形的对称图形时,可以先做出一些特殊点的对称点,然后再连接 好。我们看一个练习,求做三角形 a、 b、 c 关于直线 l 对称的三角形 a 撇、 b 撇、 c 撇。同学们可以动手画一画。 下面有三位同学的做法,我们一起来点评一下。 我们可以看到甲同学他画的 a 撇、 b 撇、 c 撇的位置都是正确的,但是在连线的时候,很明显他没有用尺子,那不是很规范。我们看一下乙同学的画法,乙同学用直尺 连出了这个对应的直线,但是我们能看出他画出的图形和原来三角形是不全等的。 我们能看出他画的对应点 a 撇是不对的,也就对应线段 a a 撇,他不是被对称轴 l 垂直平分的, 大家还发现有什么问题吗?对,他没有标上对应的字母。我们来看一下丙同学的画法,三个对称点的位置都找对了, 连线用直尺连起来,并且都标出了对应的字母,画的非常规范。 我们再来看一遍作图过程,分别做三角形三个顶点。关于直线 l 的对称点, a 撇、 b 撇、 c 撇。 顺字连接 a 撇、 b 撇、 b 撇、 c 撇和 c 撇 a 撇,这样就能得到三角形 a b c。 关于直线 l 对称的三角形 a 撇、 b 撇、 c 撇。因此,同学们一定 要养成规范作图的好习惯,练习把下列图形补成关于直线 l 对称的图形。 同样的,还是先做出这三角形三个顶点。关于直线 l 的对称点,我们可以发现点 c 是落在直线 l 上的,因此点 c 关于直线 l 的对称点就是它本身, 也就是说点 c 撇和点 c 是重合的,因此我们只需要画出点 ab 关于直线 l 的对称点 a 撇 b 撇啊,连接 a 撇 b 撇 b 撇 c 撇 c 撇 a 撇,则三角形 a 撇 b 撇 c 撇。即为所求。我们将图一中的三角形不动,将对称轴 l 向 向左平移一定的距离,就得到了第二个图中的问题。同样的,我们做出这三个点关于直线 l 的对称点,我们发现点 c 的对称点落在了直线 l 的左侧,顺次连接即可。 因此做已知图形的轴对称图形,不同的对称轴对应于不同的轴对称图形, 对于第三个图形,它是一个四边形,我们可以发现这两个点是落在直线 l 上的, 因此我们只需要做出左边这两个点。关于直线 l 的对称点,连线的时候不要忘了连直线 l 上的这个点 顺字连接。对于第四个图,我们发现它的特殊的对应点应该有五个,其中有一个点在直线 l 上,因此我们可以做出这四个点。关于直线 l 的对称点, 此时直线 l 是斜着的,因此我们可以要将三角尺斜过来去画对应的垂线, 做出这四个点的对称点,然后顺次连接就得到了它关于直线 l 对称的图形。 因此,做已知图形的轴对称图形,关键在于做出已知图形中一些特殊 勾点的对称点。我们将刚刚画好的这两个图形放在这。对于第一个图形五边形,我们从它的一个顶点出发,每隔一个点连一条线段, 大家可以看一看画出来的是一个什么图形呢?诶,是一个漂亮的五角星。同样的,对于第二个像风车这样的图案,我们也可以看成是由一个三角形经历一次、 两次、三次轴对称后形成的图形。在生活中,人们常常用轴对称进行图案设计,那同学们 回去之后也可以用简单的几何图形去设计一个美丽的图案。至此,我们可以得出做一个图形的轴对称图形的一般方法。 几何图形均可看作由点组成。对于某些图形,只要画出图形中一些特殊点,如线段端点、几何图形的顶点,他的对称点,连接这些对称点,就可以得到原图形的轴对称图形。 我们还发现对称轴向的点的对称点就是它本身, 不同的对称轴对应于不同的轴对称图形。例题,如图,是一只停泊在平 近水面上的小船,它的倒影应是图中的哪个选项? 我们可以进行分析啊。小船和它的倒影应该是关于直线 l 呈轴对称的,因此我们可以做出这个小船关于直线 l 的轴对称图形。那我们可以看到应该选的是 b 选项。 如图,有一个英语单词,三个字母都关于直线 l 对称,请补全字母,补全后的单词是, 那么这个图形是关于直线 l 对称的,因此我们可以做出这个图形关于直线 l 的对称图形, 那么我们可以看出补弦后的单词是 b、 e、 d。 下面我们来看一个折纸有关的问题。 将一个正方形纸片依次按图一中的 a、 b 的方式对折,然后沿图 c 中的虚线裁剪成图 d 的样子,将纸展开铺平,所得到的图形是图二中的哪个选项? 好,我们来分析一下。按照 a、 b 的方式对折,应该是将这个正方形纸片先往上翻折,再往右翻折,得到对应的图形 c, 然后减去 左上角和右下角的两个直角三角形,以及右下角的这个四分之一圆,得到的对应的图形。那么对于这个问题的话,同学们可以拿一张正方形的纸片动手操作,剪一剪,试一试。 当然我们也可以利用我们学过的轴对称的知识逆回去思考。我们知道折叠和展开是互逆过程,因此我们可以将最后得到的图形 根据对折方式逆回去还原,那么这一步是向右翻折,因此我们可以将它向左还原,我们可以做 这个图形。关于这条红色直线的轴对称图形,那前一步是往上翻折,因此我们应该是往下还原, 因此我们可以做这个图形。关于这条绿色直线的九对称图形,这样我们就得到了展开之后的图形。因此这个题目的选应该是选择的是 d 选项, 同学们可以用折纸的方式试一试,当然也可以锻炼一下你的空间想象能力。那么利用折对称的姿势逆回去思考,动手试一试如何剪。能剪出 b 选项,那我们可以将 b 选项按照图一中 a b 的方式进行对折。 a 的话是向上对折,所以将 b 选项的图形向上对折,那么上下是重合的,再按照图 b 的方式左右对折, 左右是重合的,因此就得到了右半部分的图形。我们来看一下向上对折,向下重合,得到上半部分图形。左右对折, 左右重合得到右半部分图形。因此我们只需要剪掉左上角和左下角这四分之一个圆,以及右下角的这个直角三角形, 那么就可以得到 b 选项对应的图。因此同学们可以通过动手操作试一试,那么也可以利用轴对称的知识 来解决这类问题。我们来看一个练习,如图所示,把一个正方形的纸片三次对折后,沿虚线剪下。三次对折, 先向上折,再向右折,再向右下方折,然后再沿虚线剪开,得到了这个图形。问,展开铺平后纸片所得到的图形是哪个选项? 同样的,大家也可以回去拿纸片动手试一试,我们也可以利用九对称的知识逆回去思考。我们将最后得到的图形去进行还原,向右 下方折,因此我们可以沿着左上方进行还原,再向右折,那我们可以沿着左边进行还原, 向上折,因此我们可以向下进行还原,这样的话,我们就得到了展开铺平后的纸片。那么应该选择的是 c 选项, 那么是否能够剪出其他几个选项呢?那我们可以看到,如果要剪出其他几个选项,那每个图形是要能够折叠三次的, 也就是说这个图形上下是对称的,左右是对称的。那我们明显能看出 d 选项是 不符合条件的,它的上下是对称的,但是它的左右是不对称的,因此我们应该能折出对应的 a、 b、 c 三个选项。 那么如何能够剪出 a、 b、 c 这三个选项呢?那么 c 选项刚刚我们已经剪过了, 那我们再看一下对应的 a 选项。对应的 a 选项的话,先向上折,剩下了上半部分图形,再向右折,剩下了右半部分图形,接着再向右下方折,因此它剩下的是这样的一个梯形, 因此我们可以发现它实际上是在三次对折之后,减去了左下角的这个直角三角。 行,这样就能得到对应的 a 选项。我们再看一下 b 选项,同理,先向上折,再再向右折,再向右下方折, 那么得到的是这样的一个四边形,那么我们可以发现他应该是少了上面的这一块, 因此它应该是减去了右上角的这个小三角形,那么得到了对应的 b 选项的图形, 而至于这一类问题的话,我们可以动手操作,那么也可以利用轴对称的知识那么去进行分析。 我们在这节课中学习了做简单平面图形。关于给定对称轴 的对称图形,主要用到了轴对称的性质,连接任意一对对应点的线段被对称轴垂直平分。 做图的一般思路是将图形的轴对称问题转化成点的轴对称问题,因此关键在于做出图形中一些特殊点的对称点。 不同的对称轴对应不同的轴对称图形, 那么我们还利用了轴对称的性质,解决了倒影、折纸、剪纸等实际问题。今天的课后作业有两道题,第一个题,把下面的图形补成关于直线 l 对称的图形, 那我们可以看到这三个图形都是不太规则的图形,那么对于第一个图形的话,我们可以做出这三个点关于直线 l 的对称点,那么连接即可 啊。对于第二个图形的话,它实际上我们可以看到它是由六个点所确定的,因此而这其中有四个点是在直线 l 上的,因此我们只需要做出这两个点关于直线 l 的对称点, 然后再对应的连接啊。此时不要忘记了连接对称轴 l 上的这个点。对于第三个图,我们应该知道他对称之后应该是一个五角星, 那么它有两个点是在直线 l 上的,因此我们只需要做出这一二三四个点关于直线 l 的对称点,然后依次连接即可。 同学们在画完他的对称的图形之后,一定要检查一下,看一看他折叠之后是否能够完全重合 好。第二题,将一个长方形的纸片按如图所示的方式对折 啊。第一个应该是先向右折啊,图二是向右上方折,然后沿着图三的虚线进行裁剪,得到了图四,那么最后 将图四的纸片展开铺平,得到的图形是那同样的,对于这个问题的话,我们也有两个思路, 一个是我们可以找一张长方形的纸片,按照他如图所示的方式动手操作剪一剪。当然,我们也可以利用我们所学的轴对称的知识来进行分析,可以提高我们的空间想象能力。对于图四这个图形, 我们可以把它逆回去还原,它是向右上方折,所以我们可以先把它向左下方还原, 接着他是向右折,所以我们可以把这个得到的图形再向左进行还原。这样的话,我们就可以得到他展开之 后的图形啊。同学们可以动手试一试。同样的,我们还可以进一步思考, a、 b、 c、 d 这四个选项是不是都能够按照这样的方式对折能够剪出来? 如果能剪出来,那么应该如何剪?同学们可以回去继续思考一下。 好,今天的课就上到这里,同学们再见!
220在线学习初中部 03:37查看AI文稿AI文稿
03:37查看AI文稿AI文稿生活中有很多轴对称的影子,比如俄罗斯国旗、喜字、窗花、剪纸、雪花等等。若把这些图形像这样对折,折痕两旁的部分就完全重合在一起了, 像这样的图形就叫做轴对称图形。折痕所在直线就是他们各自的对称轴。我们也可以说这些图形关于某条直线对称,比如雪花。关于直线 a 对称。 需要注意的是,轴对称图形是针对一个图形而言,看这个五角星,我们给他的每个角都标上字母,中间这条直线记做 l。 沿着直线 l 对折,可以发现直线 l 两边的图形重合了,说明 这个五角星是轴对称图形,直线 l 就是他的对称轴。对折后, b 点和一点重合,我们就称 b 点和一点为对称点,或者说 b 点和一点是关于对称轴 l 的对称点, c 点和地点重合也是对称点。如果我们把这个五角星沿直线 l 剪开,分成两半,现在他就变成两个图形了。沿着直线 l 折叠,这两个图形完全重合, 这时我们就说这两个图形关于直线 l 乘轴对称,但不能说他们是轴对称图形了,因为现在这是两个图形了。 如果把成轴对称的两个图形看成一个整体,那么他就是一个轴对称图形了。 如果把一个轴对称图形的两部分看作两个图形,那么这两个图就成轴对称了。 另外,同学们要注意一点,既然两边的图形是重合的,那也就是说两边图形是全等的,他们对应的角和线段也都相等。接着我们来看一道题, m、 p 分别是三角形 abc 的边, abbc 上的点, 在 ac 上求做一点 n 是三角形 pmn 的周长最小。由于三角形 pmn 的周长等于 pm 加 mn 加 np, 而 pm 是定值,故只需在 ac 上找一点 n, 使得 mn 加 np 最小即可。首先 我们做点 p。 关于直线 ac 的对称,点 p 撇连接 mp 撇,交直线 ac 与点 n, 再连接点 n 和点 p。 由轴对称的性质可知, np 等于 np 撇。因此三角形 pmn 的周长也可以写成 pm 加 mn 加 np 撇。因为两点之间线段最短, 所以当 ac 上的点 n 同时在线段 mp 撇上时, mn 加 np 撇最小,此时的三角形 pmn 周长也最小,最小值等于 pm 加 mp 撇。 最后总结一下,把一个图形沿一条直线折叠,直线两旁的部分如果能够互相重合,这个图形就叫做轴对称图形,这条直线就叫做他 对称轴。把一个图形沿着某一条直线折叠,如果他能够与另一个图形重合,那么就说这两个图形。关于这条直线成轴对称折叠后重合的点是对应点,叫做对称点轴对称的两。
312解物说理 27:03
27:03 03:23
03:23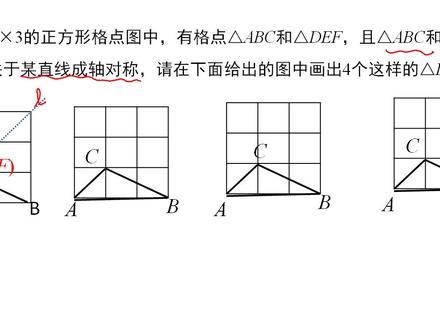 19:44查看AI文稿AI文稿
19:44查看AI文稿AI文稿各位同学大家好,我们上一节课学习了与线段的垂直平分线有关的作图,那么这一节课呢,我们继续来学习作图,主要的是画作对称图形。 那么请大家看,我这里面有一个有一幅画,再有一根直线,现在请你以这条直线作为对称着画出关于这条直线对称的这个图形的另一个部分,那么能画的出来吗? 那么这样呢?我们这幅图案就是关于这条直线成做对称的。那假如我再给你一条直线,叫你把这幅画关于这条直线对称,我们又可以画出来。如果接着画 右边的这根直线,都是左边这个图案,左边这个图案 跟这一条直线这个图案,这两个图案关于这条直线对称。那么经过这样画,我们就可以画出一幅很美的图案。这个图案呢,实际上是都是做对称的。 那么大家继续看,假如我给你这个图案,再给你这样一条直线,要你画出这个图案,关于这条直线成主对称的图形,能画的出来吗?同样的我们可以画出来,对吧? 那假如再给你一条直线,把上面这两个图案看作一个整体,让他关于这条直线对称,画出他的对称图形,那我们又可以设 记错这样的一个比较漂亮的图形。再比如说我这里面给你一个福的灯笼,给你不同的对称着,那么我们就可以设计出这样的一幅福的灯笼的图案 啊。利用着对称,我们可以设计出一些很美的图案。好,那现在我们就来做一做, 请大家在一张半透明纸的左边部分画一只左脚印,然后把这张纸对折以后描图,然后打开对折的纸,我们就能得到相应的右脚印了。 我们把它把这张白纸透明的白纸对折对折以后描图, 秒了以后得到的就是右脚印,得到就是相应的右脚印。那么请大家注意观察,仔细观察这个图,左脚印和右脚印有什么关系?左脚印和右脚印什么关系啊?是不是称左对称啊? 再看这个对称着呢,是折痕所在的直线,也就是直线 a l。 那么这个直线 a l, 它与图中的线段 p p p 是什么关系呢? p 顶 p p 顶是一堆对称顶啊。这是什么关系啊? p p p 与 a l 什么关系啊? 是不是对称着 l 就是线段 p p p 的垂直平分线啊。那也就是说明直线 l 垂 直平分线段 p p p 对吧?直线 l 垂直平分线段 p p p。 好,我们归纳一下。 有一个平面图形,我们可以得到与他关于一条直线 l 对称的图形。一个平面图形,比如这个脚印 给你一条直线 l, 那我们就可以得到关于这条直线对称的图形。那么这个图形 画出来的这个图形与原来的图形形状和大小是完全相同的。这是第一个特征,画出来的这个图形和原来的图形形状和大小完全相同。第二个特点就是新图 图形上面的每一个点都是原图形上面的某一个点。关于这条直线 l 的对称点,你像 p p, 我可以在原图当中找到 pd 音。关于执行 l 对称 第三个特点,我连接任意一对对应顶的线段,都被对称着垂直平分。比如说我连接任意的这个顶 p 顶 p p 这一对对称顶,它都被这条直线 a、 o 垂直平分。 这是一个平面图形啊。我可以得到与他关于一条直线。哎呦,对称的图形。对称的图形。那么这个对称的图形跟原来的图形有什么有什么 特点呢?对称的图形与原来的图形形状大小是完全相同的。新图像新图形上面的每一个点都可以在原图形上面找到一个点。关于 l 对称。 第三个呢,就是零级任意一对对称点,这样的线段都被对称着垂直平分,都被对称着垂直平分。好利用这样的性质,我们来做两例题。你 将一张正方形纸片,按照图一、图二所示的方向对折,然后沿着图三中的虚线剪裁,就得到了图四。那么将图四的纸片展开铺平,那么再得到的 图案是哪个呢?看看再得到的图案是哪个?对折,再对折,然后紧,那么再得到的图案是哪个啊? 我们只要动手做一做,紧一紧就可以得到了。是哪一个啊?就是 b, 就是 b, 就是这个形状,动手做一做就可以出来了啊。动手做一做好,我们再看一二。 如图将长方形 a、 b、 c、 d 沿着 d、 e 折叠,使得顶 a 落在 b、 c 上面的 f 处。 如果角 e、 f、 b 这个角等于五十度,那么角 c、 f、 d、 d 的度数为多少? cf 角 cfd 的度数为多少?那么将长方形 a、 b、 c、 d 沿着 d 一这个折叠,那么折叠说明 d 一就是对称着折叠过来。这两个图形实际上就是关于 d 一 乘着对称对吧?那么乘着对称的两个图形一定是全等的图形对吧?所以这个是九十度,那么这个角也是九十度对吧? 那么这是五十度,那么这个角呢?就是四十度了吗?所以角 c、 f、 d 的度数,那么就是选 c 了,四十度。说明一下,折叠实际上是一种做对称变换,折叠前后的图形形状和大小是不变的,对应边和对应角 都是相等的。折叠啊。折叠是一种左对称病患,像我们刚才把那个脚面折叠,折叠是这样,两个图案就是完全形状大小完全相同。好,下面我们就来学习如何做左对称图形。 那么如何画出一个顶的做对称图形呢?我这有一条直线, l 还有一个点哎,那么现在请你画出点关于这条直线哎呦的对称点。 ap。 我们从最简单的开始 画一个点关于 l 的对称点,那怎么画呀?第一步,根据大家想,假如我已经画出来了,心想啊,假如已经画出来了, 那么顶 a 和顶 ap。 关于 l 对称,那么把 aap 连起来,这一对对称顶的零线是不是 b l 垂直平分啊,是不是 b l 垂直平分啊。 所以我们画的时候怎么画呀?我只要过 a 点做 l 的垂线,做了垂线以后,然后在这个垂线上面 找到这么一点,比如这一个 hap 跟 ha 相等就行了。那就这样画。那么对称点呢?我们就画出来了,就是让 l 成为 aap 的吹的平分线。 所以做法的第一步,固定 a 做 l 的垂线,垂着为 o。 第二步 在垂线上面汲取 o a p 是等于 o a, 汲取 o a p 是等于 o a, 那么顶 a p 就是顶 a。 关于直线 a o 的对称底,那么这就画出来了,大家看到了吗?怎么画? 因为 aap 这条线段被直线 l 垂直平分,所以第一步就是过顶 a 做直线 l 的垂线,找到垂着, 然后在垂线上面汲取 o, a p 等于 o a, 也就是让 o 零成比。 a i p 的终点又是垂线又是终点,那么 a o 就是垂的平分线了,对吧?这就画出来了。好,那么一个点关, 一条直线的对称点我能画出来了。那下面接下来你能不能画出一条线段关于某条直线对称的线段呢?同样的我们可以画。 那如何画一条线段的对称图形呢?要画线段,我们关键就是确定线段的两个端点,是不是找到两个端点就行了,怎么画呀?找到 a 点关于 a o 的对称点 a p, 找到 b 点关于 l 的对称点 b p, 然后 a p b p 一零就是 a b。 关于直线 l 对称的线段,这就画出来了,你们看到怎么画呢?画出线段 a b 的两个端点关于 a r 对称的对称点。对称点找出来,一拧,这条对称线段就画出来了。那我们再看 线端 ab, 如果是这样放的, b 点正好就落在对称着上,那么 b 点关于 l 的对称点,对称着上面的点就是它本身啊,就是它本身。 对称主上面对应顶啊,对称顶就是它本身。所以我只要画错 a 顶关于 l 的对称顶 ap, 那么再把这个 b 顶 bp 顶是重合的,然后再把 apbp 连起来就行了。 那假如 ab 两点分布在直线 l 的两侧呢?画的方法一样,画出 a 点关于 l 的对称点 ap, 再画出 b 点关于 l 的对称点 p a p b p。 大家注意,你在画的时候,线段 a、 b 和线段 a、 p、 b、 p 相交,焦点一定落在对称桌上,焦点啊,一定落在对称桌上。如果你焦点不画在对称桌上,那么你就画的有问题喽。 好,这是画一条线段的对称图形,我们可以把它画出来。 那么想一想,假如说我现在不是线段的,我现在有一个图形和一条直线,那么如何画出与这个图形关于这条直线对称的图形呢? 我们看第三,假如我现在这里面是这样一个三角形 a、 b、 c 还有一条直线。哎呦,请你做错 三角形 a、 b、 c 关于直线 l 对称的图形做错。与三角形 a、 b、 c 关于直线 l 对称的图形。那怎么画呀? 三角形啊,这三个顶顶吗?三个顶顶定下来,是不是这个三角形的形状就定下来了,三角形的位置就定下来了。所以我们只要 找到 a 点、 b 点、 c 点这三个点,关于 l 的对称点就可以画出来了。是不是? 然后连接这些对称点,我们就能得到所画的图形?好了,动作画一下。故 a 点画直线 l 的垂线,然后得到垂着为 o, 在垂线上面截取 vp 等于 v, 那么 ap 点就是定 a 关于直线 l 的对称点。下面接下来同理,我分别画错 b 点关于 l 的对称点 bp, 再画作 c 点关于 l 的对称点 cp, 那么三个对称点都有了。然后只要连接 apbpcp 就得到了三角形 a p、 b p、 c p 这个三角形 a p、 b p、 c p 就是我们所要求做的三角形。会了吗? 一个图形啊,我只要找到图形上面相应的点,他的对称点,对称点找到了,那么这一个图形只要把线段选刺连接起来,就可以得到我们所需要的三角。 行了,这就画出来了。好,那我们总结一下做左对称图形的方法。 几何图形我都可以看着是由点组成的,那么对于某些图形呢?只要做错图形中一些特殊点,比如线端的端点啊,做错特殊点的对称点, 然后连接这些对称点,就可以得到原图形的做对称图形。会了吗? 因为几何图形都是由点组成的,所以呢,只要找出图形当中的特殊点,特殊点,做出它的对称点,然后连接这些对称点,就可以得到原图形的做对称图形了。好,下面呢我们再看个例题。 在三乘三的正方形格点图中,由格点三角形 a、 b、 c 和三角形 d、 g、 f。 并且呢三角形 a、 b、 c 和三角形 d、 g、 f 是关于某一条直线呈着对称的。 请你在下面给出的图中画出四个这样的三角形 d、 g、 f, 要你把这个三角形 d、 g、 f 画出来。这里面啊点了三角形 a、 b、 c, 那么三角形 d、 g、 f 在哪个位置?是由它的对称着所确定的,对不对?所以呢,你首先来找对称着的位置。假如说我的对称着是这一条正方形的这样一条对角线,那么你能 能不能画出三角形 a、 b、 c。 关于这条直线 l 对称的三角形啊,把这个 dj f 就画出来。这里面关于直线 l 对称。那么 这个 a 点的对称点,一点的对称点, f 点的对称点。大家看 a 点的对称点, d 点是不是就是跟 a 点重合啊?那么 c 点的对称点呢?是不是就是跟 c 点重合啊? f 点。那 b 点关于 l 的对称点呢?是不是就是这一个点啊?那么三个点找出来了,这个三角形不就画出来了吗?对吧?所以三角形 d、 e、 f 与三角形 a、 b、 c 就关于这一条直线对称了。这是正方形对角线所在的直线。那假如我把对称轴的位置 再换一换,比如说我把对称着换成这样过来的。对角线所在的直线,这个是对称着。那么你怎么画呀?那么找到我找啊, 现在你就找啊,找对称顶啊。 c 顶的对称顶是不是就在这个地方啊? b 顶的对称顶是不是就是它本层啊?那么 a 顶的对称顶在哪里啊? 嗯, a 顶的对称顶是不是就在这啊? c 顶的对称顶呢?是不是 c 顶的对称顶在这?那么 a 顶的对称顶在哪里啊?你能不能找的出来啊?那都可以把它找出来啊。 那 b 点它的对称零一点跟它重合, c 点它的对称零就在这个地方。那么 a 点 它的对称点就在这个地方。那么三个点找到了,所以这个三角形我们就可以画出来了,对吧?对称着在这。 那假如我们把对称轴的位置再换一换,比如我这个对称轴就在这儿,那么 c 顶它的对称顶就在这个位置,对吧? a 顶的对称顶呢,是不是就跑到这儿啦?那 b 顶的对称顶呢?是不是就跑到这儿啦?所以呢, 这个对称顶找到了,那么相应的三角形我们就画出来了,对吧?好,那么这个对称着是这一条啊。现在我们把对称着再换一换, 假如我的对称着是这样一条直线呢?是这个三乘三方格的这个中线中间 这样一条线。那我们找找看, c 顶的对称顶是不是就跑到这了? b 顶的对称顶是不是就跑到这了? 那么 a 顶的对称顶呢?是不是就跑到这了?所以我们就可以对称顶找到了,那么这个三角形我们就可以画出来了,对吧? 所以这里面要你画出四个这样的三角形。 djf 那你就给我找出四条不同的直线作为对称着,那么就可以把相应的图形呢画出来了。 这是画图总结一下方法,做一个图形关于一条已知直线的对称图形,关键就是做错图形上面一些点关于这条直线的对称点,然后我们再根据 已知的图形将这些点呢连接起来,那么就得到了我们所要求做的图形。好,那我们这一节课呢,主要的是讲的如何做做对称图形, 我们的方法就是先找对称底,然后再把对称底呢拧起来。大家这个画做对称图形会了吗? 那么课后请同学们把课本上面六十八一本逆袭两个题目呢,大家把它画一画。我们这节新课呢就先讲到这,各位同学再见。
14爱笑的石榴276 06:47查看AI文稿AI文稿
06:47查看AI文稿AI文稿今天我们来学讲初二上数学第十三章的 轴对称,我们来看这道题。如图,在三杠三的正方形网格中,格线的交点称为格点, 以格点为顶点的三角形称为格点三角形。比如像这个图中的三角形 abc, 图中的三角形 abc 为格点三角形在图中最多 能画出多少个格点?三角形与这个三角形 abc 呈轴对称, 我们说那个轴对称的,他是这样的,如果一个平面图形 沿着某条直线折点与另个图形能够互相重合,我们就说这两个图形呈轴对称,那你要考虑 要使这个三角形 abc 和另一个三角形呈轴对称,那我们首先要确定 对称轴,那么确定对称轴的话,在这个网格中到底是以边为对称轴还是以对角线呢?比如我们以 bc 所在的直线作为对称轴,那肯定我可以这样画吗?好 觉得这个鸡不地, 那么很明显我们就可以得到三角形 dbc 和三角形 abc 是成轴对称的。那么除了这种以外,我们又来考虑, 如果不是以经过格点的将的两个点之间啊所确定的直线为 对成轴,比如像我们来找这个假设经过他们的中间的这样的,能不能 也做过一条对称轴呢?比如像我们这样画,然后将你计为 c 片,这个时候三角形 abc 片 和这个三角形 b ac 片啊 b ac 他刚好是关于这条直线对称的。好,那么这个第二种也可以的,因为第三种我们来看还有没有呢? 如果有的话,我们再来看。比如像第二个图中是经过 这里啊,连线他所在直线,如果是以这条呢?你们好,我观察 是不是也可以找到从左腿上的三角形,那这个时候我们可以往这个方向画呢?那么得到这个三角形, 如果把它记为第一 f, 那很明显三角形低于 f 和三角形 abc 啊,也是成组对成,还有没有呢?我们是刚才所考虑的, 他的对称轴可能是这种纵向的,有没有可能是横向呢? 你要找到横向的话,就比如像我们过中间这里 做这条直线,把这条直线 作为对称轴的话,他可能会是什么情况的?好,我们来观察啊,像这种情况下得到的 三角形,如果继承了 a 片 cb, 他与三角形啊,这个 abc, 他也是成走对称的。 我们再来看刚才所讲的横向纵向的找对称轴,他有没有可能是对角线呢? 打个比方,这样的观察,他是不是可以以这条为对称轴,那么以这条为对称轴的话,这个时候他的图形 可以这样的话呢? 啊,那么这个三角形 假设把它记成 d、 e, 那么三角形 a、 d、 e 和三角形 a、 b、 c, 他也是成组织成, 那既然这样讲的话,说明还有吗?比如像他过的是这两个点 啊,所确定的直线为对称轴,比如像这样的话, 那这个时候这个图形我们又怎么画出来的?我们换一个方向的,这样 这个三角形 d、 e、 f, 很明显他和三角形 b、 ac, 他是关于这条直线对称的, 那么我们就从横向、纵向,然后对角向来确定他的对称轴,从而找到另外个三角形和三角形 abc, 从轴对称,那还有没有呢? 其实我们三个方向都走了以后,他就只有六种, 所以这里最多能画出六个格点。三角形与三角形 abc 呈轴对称,你听懂了吗?
75阿呆工作室 06:30
06:30 03:23
03:23







