可以吧?假如说绕着点 o 进行旋转的话,那我们给他连一下 oa 吧,连 oa, 那你看这个 a 点是在横着的三个格,竖着的两个格,这样的一个正方形,那长方形的对角线吧? 那我们给他逆时针旋转九十度,逆时针旋转九十度,这是横三竖二,对吧?横着三个,竖着两个,那挪过来了之后,给他旋转九十度,这个长方形旋转过来了,就是横三 二。给他这样旋转九十度了之后呢?这个三个格是不是就旋转到这来了?那就是横二竖三吧?横二竖三,所以这是不是那个长方形?所以他是不是就在这 对角线这个点了?所以这个 a 点是不是就跑到这这个位置了?能动吗? 横三竖二旋转过来了之后就是横二竖三,是不就交换位置,交换竖,对吧?因为是我们旋转的,是这个长方形吗?竖着三个,横着两个,这个是横着三个,竖着两个,所以这是不是就是那个 a 点了, 对吧?然后 c 的这个我们就连接 oc 吧,你看这个 c, 这是 a 的那个 c 所所载的是什么? c 所载的是 横二竖几四?横二竖四吧,所以 他要旋转过来了,就成了倒过来了,就成了什么横四竖二吧,所以横四,那就是一二三四,竖二是不是在这个位置? 横四从原点往这数,一个、两个、三个、四个,竖二,是不是到这个位置了,对吗?是不是这个?这是那个长方形,所以这是那个对角线的那个点吧?是不是这个 oc 就旋转到了是 这种程度了?所以这是不是那个 c 点所对应的那个点?然后同样的道理,我们连接 ob, 那你看这个 b 是竖着,横着应该是多少这个点,这是横一横着,一个、两个、三个、四个、五个,这是不是横五竖着呢?一二三四 五,是不是横五竖五?所以到这边也得是横五竖五吧?那我们给他长得就是横着,一个、两个、三个、四个、五个,竖着是一个、两个、三个、四个、五个,是不是到这了? 所以这是那个 b 点所对应的位置吧?所以当他旋转九十度,是不是就是从了 ob 到了这这个 ob 了?所以新的图形就是 旋转九十度之后是不是就变成了这个图形了?能理解吗?你自己试试,我把它往这边旋转九十度,顺时针旋转九十度。
粉丝337获赞3329
相关视频
 06:42
06:42 07:35
07:35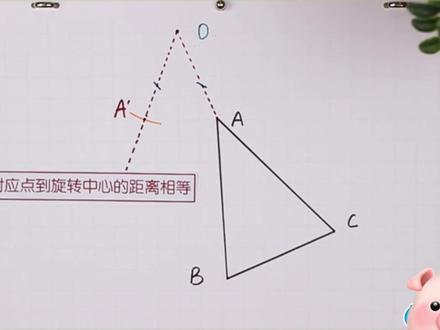 02:22查看AI文稿AI文稿
02:22查看AI文稿AI文稿上一讲,我们看了各种转啊转的东西,从而了解了旋转的性质。不过旋转这一张最有趣的莫过于自己动手去体会图形的旋转。所以接下来我们做这样一件事,画出旋转后的图形, 第一个任务就是画这个图形,逆时针旋转四十五度的样子。嘿嘿,开玩笑啦,杨从军这么善良,不会整你的。我们要画的模特是这货三角军。 画任何旋转图形之前,有两个关键点需要注意,一是旋转中心,也就是围着哪里转。二是旋转的角度,也就是转多少度。好,开始吧。第一个任务是画三角均绕欧点,顺时针旋转四十五度的图形, 也就是说旋转中心是欧点,三角军绕欧点转起来大概是这么个效果。但是我们要画的是旋转 四十五度后的,不能随便转。另外,包括三角形在内,一切几何图形都是由点构成的。所以画旋转后的图形这件事,可以转化为找 abc 三个顶点旋转后的对应点, a 撇、 b 撇、 c 撇的位置,再连接他们,就能得到旋转后的三角形了。 明确了这点后,下边的任务就是找 abc 三点顺时针旋转四十五度后的对应点, 先从 a 点开始,转完后的 a 撇点大概在这一块,但按顺时针旋转四十五度后,具体在哪呢?注意,我们要这样画, 先连接 ao, 也就是联二旋转中心,这样就有条线段了。然后我们要基于这条线段画一个角,哎,画多大呢?估计能猜到,就是四十五度的角, 用两脚气或者三角板就能找到和 ao 乘四十五度角的射线,这样就有四十五度角了,那么我们要找的 a 撇点,他就在这条线上,那具体在哪呢? 旋转有这么条性质,对应点到旋转中心的距离相等,也就是旋转后得到的 a 撇点到欧点的距离和原来 a 点到欧点的距离是相等的。 那就好办了,直接用圆规取 ao 的长度,然后在这条射线上以欧为圆点结一下 a, 就有了 a 撇点了,因为 ao 等于 apo 对应点到旋转中心的距离相等。这样呢,我们就找到了 a 点顺时针旋转四十五度后的对应点 ap。
2377洋葱学园App 02:09
02:09 03:50查看AI文稿AI文稿
03:50查看AI文稿AI文稿嗨,同学们好,我是艾瑞克老师,学习了旋转的概念和性质。今天呢,我们来学习旋转作图,也就是给出一个平面图形。已知旋转方向和旋转角以后,如何画出旋转后的平面图形? 在分析旋转过程的时候呢?我们知道三个一记,一个定点,一个方向,一个角度。例如,两个旋转中,旋转中心相同,旋转角和旋转方向不同,会产生不同的旋转效果。 那也是两个旋转,旋转中心和旋转方向不同,旋转角相同,也会产生不同的旋转效果。 所以呢,旋转作图要保证三个一相同。根据旋转的性质,我们呢,总结出旋转作图的具体步骤。 例如,把三角形 abc 绕点钩顺时针旋转六十度后,是确定点 abc 的对应点的位置,并画出旋转后的三角形。 第一步,定既确定原图形中每一个关键点与旋转中心。三角形 abc 的关键点呢,就是三个顶点 abc, 旋转中心呢是 o。 第二步,连,即连接图形中每一个关键点,于旋转中心连接 a、 o, b、 o, c、 o。 第三步,转 既把连线按要求绕旋转中心转动一定的角度。阿尔法把 a、 o, b、 o, c、 o 绕点欧转动六十度, 也就是呢,做出旋转角。第四步,结记在旋转角的另一边上结取于对应的关键点到选址中心的距离相等的线段,得到各点的对应点。 由 a 撇 o 等于 a、 o, b 撇 o 等于 b, o, c 撇 o 等于 c, o, 得到 a、 b、 c 的对应点, a 撇、 b 撇、 c 撇。 第五步,连记顺次连接所得到的各对应点,连接 a 撇、 b 撇、二、 c 撇。第六步,写出结论,说明做出的图形,那三角形 a 撇、 b 撇, c 撇就是旋转后的三角形。 再例如呢, e 是正方形, abcd 中边 cd 上任意点。现在呢,以点 a 为旋转中心,把三角形 ade 顺时针转动九十度,画出旋转后的图形。 要画出旋转后的图形,关键是确定三角形 a、 d、 e 三个顶点旋转后的对应点,即旋转后他们的位置。 因为 a 是旋转中心,那旋转后的对应点呢,就是他本身。因为 d a 等于 b, a b 等于九十度,所以呢 d 旋转后的对应点是 b。 又因为旋转前后的图形全等,可以做 cb 的延长线,在延长线上截取 b, 一撇等于 d、 e 那点 e 旋转以后的对应点就是一撇三角形 ab 一撇就是旋转后的三角形。
400Erica数学 02:20
02:20 09:03
09:03 02:14查看AI文稿AI文稿
02:14查看AI文稿AI文稿这个视频里,我来给你讲讲如何画旋转图形,比如给你个十乘十的正方形网格,每个小正方形边长均为单位。一,在 这里有一个三角形 abc, 让你把这个三角形绕着顶点 c 顺时针旋转九十度,那旋转之后得到的三角形 a 撇、 b 撇、 c 撇该咋画呢?由于旋转得到的还是个三角形,那只要确定好他的三个顶点的位置就 ok 了。 这里面最简单的当然就是点 c 对应的 c 撇点,因为三角形就是绕着点 c 旋转的,那点 c 就是旋转中心,所以对应的 c 撇点当然还在这里。第一个搞定了,接下来看看 b 点对应的 b 撇点又在哪里? 由于 bc 是一条水平方向长度为三的线段,那让他绕着点 c 顺时针旋转九十度,自然会变成竖直的,也就是这样,那必撇点自然就在这里了。 最后还剩下 a 点对应的 a 撇点,他又该位于什么地方呢?线段 ac 是一条斜着的线段,那他旋转之后的情况当然不如水平的好判断,不 过也没关系,咱把这条斜着的 ac 当做这个长方形的对角线不就 o 了。如果能够搞定这个长方形是咋旋转的,只 后再确定这个对角线就轻而易举了。这个竖直的长方形,长是一,宽是三,那顺时针旋转九十度之后,自然就变成了水平方向,是一个长是三,宽是一的长方形,相应的对角线就是这条,那 a 撇点也就在这了。到此,旋转 之后的三个顶点就全部搞定了,接下来只需要把这三点连接起来即可。就是这样,这就是旋转之后的三角形, a 撇 b 撇 c 撇了。好了,就讲这么多,总结一下, 要想在网格当中画出一个图形旋转九十度之后的样子,那就得先分别找到各个顶点的位置才行,其中水平的边会变成竖直,而斜着的边也不要紧,只要 把它看成锁在长方形的对角线即可,然后旋转整个长方形就可以了。怎么样,听懂了吧?
180读书郎网校微课堂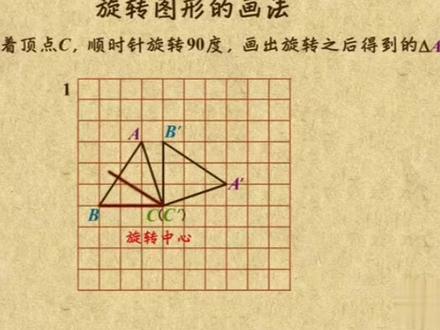 02:01查看AI文稿AI文稿
02:01查看AI文稿AI文稿这个视频里,我来给你讲讲如何画旋转图形,比如给你个十乘十的正方形网格,每个小正方形边长均为单位。一、在这里有一个三角形 a、 b、 c, 让你把这个三角形绕着顶点 c 顺时针旋转九十度, 那旋转之后得到的三角形 a 撇、 b 撇、 c 撇该咋画呢?由于旋转得到的还是个三角形,那只要确定好它的三个顶点的位置就 ok 了。 这里面最简单的当然就是点 c 对应的 c 撇点,因为三角形就是绕着点 c 旋转的,那点 c 就是旋转中心,所以对应的 c 撇点当然还在这里。第一个搞定了,接下来看看 b 点对应的 b 撇点又在哪里? 由于 bc 是一条水平方向长度为三的线段,那让他绕着点 c 顺时针旋转九十度,自然会变成竖直的, 也就是这样,那 b 撇点自然就在这里了。最后还剩下 a 点对应的 a 撇点,他又该位于什么地方呢?线段 ac 是一条斜着的线段,那他旋转之后的情况当然不如水平的好判断,不过也没关系,咱把这条斜着的 ac 当做这个长方形的对角线不就欧了? 如果能够搞定这个长方形是咋旋转的之后再确定这个对角线就轻而易举了。这个数值的长方形长是一,宽是三,那顺时针旋转九十度之后,自然就变成了水平方向的一个长是三,宽是一的长方形,相应的对角线就是这条,那 a 撇点也就在这了。 到此,旋转之后的三个顶点就全都搞定了,接下来只需要把这三点连接起来即可。就是这样,这就是旋转之后的三角形, a 撇、 b 撇、 c 撇吧。好了,就讲这么多, 总结一下,要想在网格当中画出一个图形旋转九十度之后的样子,那就得先分别找到各个顶点的位置才行,其中水平的边会变为竖直,而斜着的边也不要紧, 只要把它看成锁在长方形的对角线即可,然后旋转整个长方形就可以了。怎么样,听懂了吧,赶紧动手试试吧!
182初高中数理化老师 04:01查看AI文稿AI文稿
04:01查看AI文稿AI文稿老师,这个学校题太难了,我们会好,下面我们一起来探究画旋转图形的一些方法技巧。第一种方法呢,就是 靠我们的感觉空间的一种感觉,比如说这个直角三角形,他是个等腰直角三角形,对吗?我们想画他这样逆时针旋转九十度, 之后呢,我们先想象,但是想象的话,大家会发现靠不住,我们会想象到这样,他绕着这个点,这个三角形呢?绕着这个点逆时针旋转九十度,有可能是这样的,对吧? 是不是?这我们想象到的其实是这样的吗?我们可以借助三角板来验证一下,绕着这个点,我们按住别动,绕着点 o 逆时针旋转九十度,什么结果?应该是这样的,而不是这样的,是不是?所以想象第一种方法呢?想象 可以,但是呢靠不住,是不是不靠谱?那么我们就可以第二种方法呢,接住三角板,对吧?接住三角板,绕着这个点勾逆时针旋转九十度,哎,一画是不是就行了?这个图形呢,绕着点勾 绕着点哦,逆时针旋转九十度,是吧?顺时针旋转九十度,是这样的啊,那么看这长方形靠想象针还靠不住啊?比如说咱们去找一个实物, 这个长方形呢,我们画一个大小和他一样的,如果绕着这个点旋转呢?我们看下逆时针旋转九十度,他是这样的,对吧? 顺着旋转九度呢,绕着这个点是这样的,我们一划就可以,对吧?但是呢,第二种方法,我们用靠 食物的话也可以,但是不有点麻烦呀,总不能他出现什么通行,我们就做什么通行,对吧?所以我们最终还要考虑想一种万能的方法啊,万能方法来做好,下面来介绍, 比如这个大图啊,我们看一下绕着点哦,比如说他是逆时针旋转九十度,我们方法就是先找和这个旋转点相关连的线, 其他的线我不用看啊,先找和他相关连的线,我们先把每一条线都按一定的方向去旋转,绕着点哦,逆时针旋转九十度,那么这个竖的逆时针旋转九十度, 是不是横过来了?数格,一二三,一二三好,画下来,然后再个横的一二三,这个横的呢?横的这条线 绕着点哦,逆时针旋九十度,什么立竖起来了,横的竖起来了,对吧?然后我们数格,一二三四四格,一二三四四格,数格最后一步我们把它补齐就可以了。 好方法,你掌握了吗?再说一遍,比如长方形为例啊,长方形为例,绕着咱们这个换这啊,绕着这个点说,这是点哦,顺时针旋转九十度,我们还是找和他旋转点相连的线,其他的线我们都不看。 相连的线,那他顺着人九十度横着是不竖起来了?一二三四四个格,一二三四分别旋转竖格画线,那么下面该塌了是吧?竖着竖个竖着,这个呢? 顺时针旋转角度横过来了是吧?两格,哎,就在这重合了是吧?最后呢,我们把图补齐是不是就可以了? 这就是这个长方形绕着这个点勾,顺时针选成九十度之后的图形,在标准的话我们可以 画箭头来表示。所以总结方法,方法就是,第一呢,先找 和旋转中心相连的线,第二呢,分别把这些线旋转数格画出第三呢?把图形补前。老师我学会了耶。
140泡泡笑
猜你喜欢
最新视频
- 1.0万我是周周



